Archivo del Autor: Karen González Cárdenas

Cálculo Diferencial e Integral I: Diferenciales

Por Karen González Cárdenas

Introducción

Vimos que una forma de expresar a la derivada de una función $y = f (x)$ es utilizando la notación:
$\frac{d y}{d x} = f^{'} (x)$

Recordemos que $\frac{d y}{d x}$ es un «símbolo» que utilizamos para denotar el límite:
$lim_{Δ x \to 0} \frac{Δ y}{Δ x} .$
Por lo tanto, no consideremos a $\frac{d y}{d x}$ como una fracción donde su numerador es $d y$ y su denominador $d x$ . No obstante, en diversos problemas de aplicaciones del Cálculo es necesario dar interpretaciones separadas a $d x$ y $d y$ . En esta entrada, veremos cuál es la interpretación de estos nuevos «símbolos» y cómo su aplicación nos resulta útil.

Definición de la diferencial de una función

Definición (Diferencial): Si tenemos una función $f$ derivable. Definimos a la diferencial de $f$ como el producto de su derivada por la diferencial de la variable independiente $x$ .
$d f (x) = f^{'} (x) d x .$

Para simplificar un poco la notación consideremos $y = f (x)$ y nos quedamos con:
$d y = f^{'} (x) d x .$

A continuación, veremos algunos ejemplos donde se nos pide hallar la diferencial de una función haciendo uso de la definición revisada.

Algunos ejemplos de funciones y su diferencial

Obtén la diferencial de las siguientes funciones:

$y = x^{3} - 3 x$
$ρ = \sin (a θ)$
$t = \frac{x}{a} + \frac{a}{x}$
$s = θ c o s (θ)$
$y = \log (\sin (x))$
$γ = e^{t} c o s (π t)$

Solución: Aplicaremos la definición siguiente en cada uno de los incisos
$d y = f^{'} (x) d x .$

Para la función $y = x^{3} - 3 x$ tenemos:
$\begin{aligned} d y & = (x^{3} - 3 x)^{'} d x \\ = (3 x^{2} - 3) d x \end{aligned}$
Por lo que la diferencial es $d y = (3 x^{2} - 3) d x$ .
Ahora para la función $ρ = \sin (a θ)$ :
$\begin{aligned} d ρ & = (\sin (a θ))^{'} d θ \\ = a \cos (a θ) d θ \end{aligned}$
Concluimos que $d ρ = a \cos (a θ) d θ$ .
Aplicando la definición con $t = \frac{x}{a} + \frac{a}{x}$ :
$\begin{aligned} d t & = {(\frac{x}{a} + \frac{a}{x})}^{'} d x \\ = {(\frac{x}{a} + a x^{- 1})}^{'} d x \\ = (\frac{1}{a} - a x^{- 2}) d x \\ = (\frac{1}{a} - \frac{a}{x^{2}}) d x \end{aligned}$
Por lo tanto $d t = (\frac{1}{a} - \frac{a}{x^{2}}) d x$ .
Del mismo modo para $s = θ c o s (θ)$ :
$\begin{aligned} d s & = (θ \cos (θ))^{'} d θ \\ = (\cos (θ) - θ \sin (θ)) d θ \end{aligned}$
Así $d s = (\cos (θ) - θ \sin (θ)) d θ$ .
Y si consideramos $y = \log (\sin (x))$ :
$\begin{aligned} d y & = (\log (\sin (x)))^{'} d x \\ = \frac{1}{\sin (x)} \cdot \cos (x) d x \\ = \frac{\cos (x)}{\sin (x)} d x \\ = c t g (x) d x \end{aligned}$
Por lo que $d y = c t g (x) d x$ .
Finalmente para $γ = e^{t} c o s (π t)$ :
$\begin{aligned} d γ & = (e^{t} \cos (π t))^{'} d t \\ = (e^{t} \cos (π t) - e^{t} \sin (π t)) d t \end{aligned}$
Concluyendo $d γ = (e^{t} \cos (π t) - e^{t} \sin (π t)) d t$ .

A continuación, veremos una interpretación geométrica de la diferencial que más adelante nos permitirá revisar algunos problemas de aplicación.

Una interpretación de la diferencial

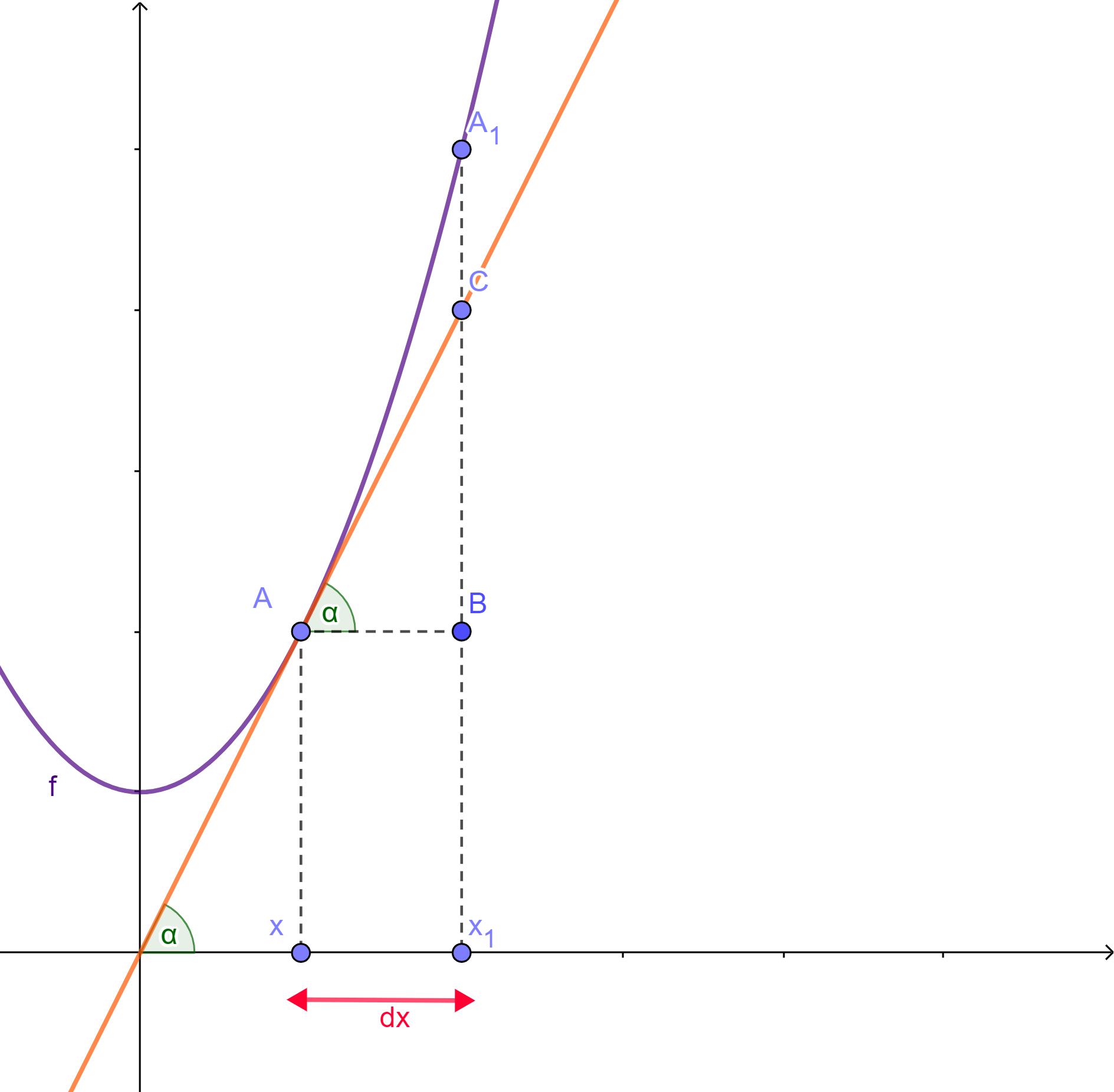
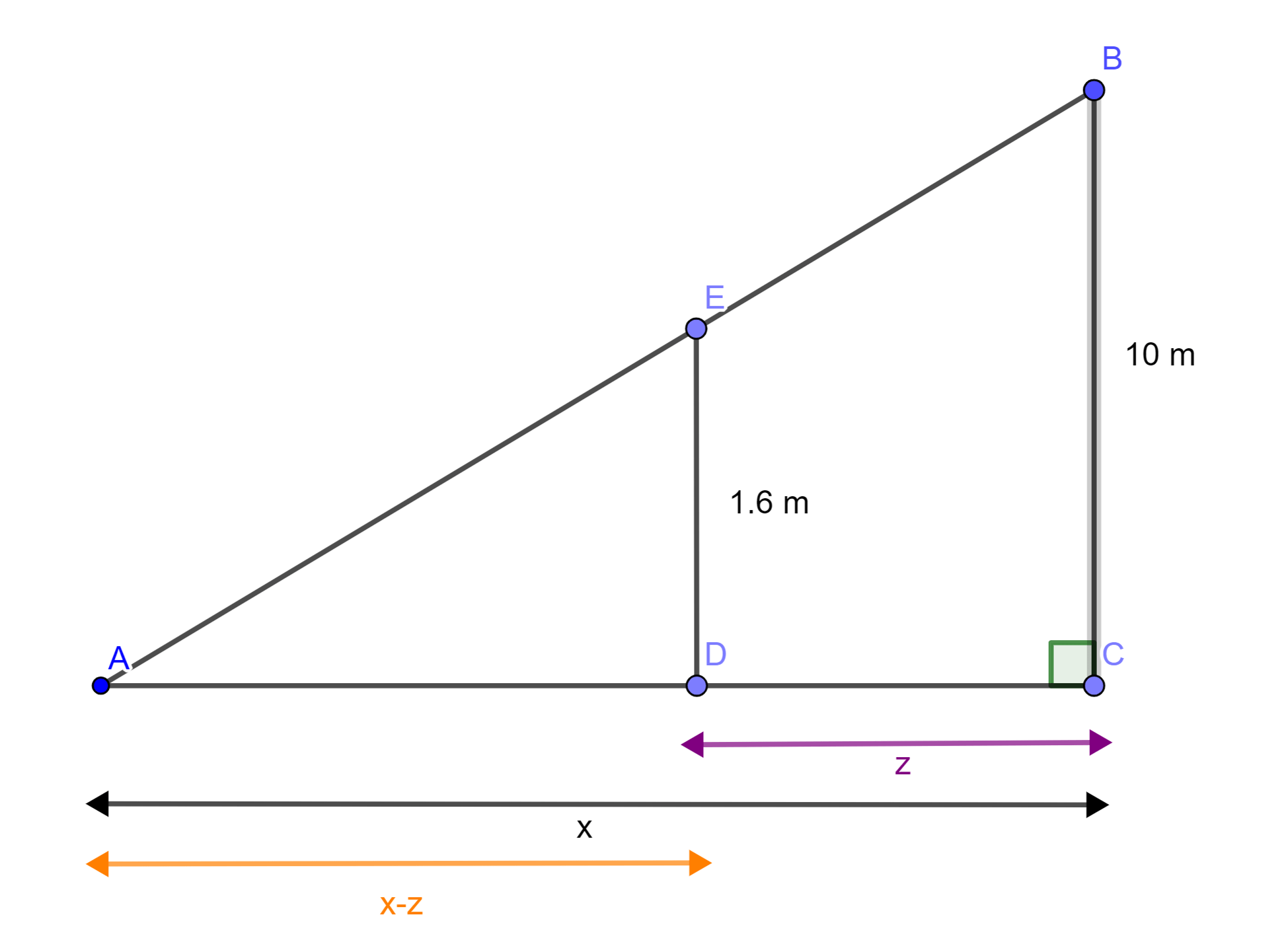
Tomemos la función $y = f (x)$ y al punto $A$ sobre la gráfica de $f$ . Consideremos a $f^{'} (x)$ como el valor de la derivada en $A$ y tracemos la recta tangente en dicho punto.

Nombremos al segmento $A B$ como $d x$ . Recordemos que la definición de la diferencial es:
$d y = f^{'} (x) d x .$

Por lo visto en la primera entrada de esta unidad sabemos que:
$f^{'} (x) = \tan (α) .$

Además, aplicando la definición de la función tangente apoyándonos en el gráfico siguiente, se tiene:
$\begin{aligned} \tan (α) & = \frac{c o}{c a} \\ (*) & = \frac{C B}{A B} \end{aligned}$

Cuando sustituimos $(*)$ y $d x = A B$ obtenemos lo siguiente:
$\begin{aligned} d y & = (\frac{C B}{A B}) (A B) \\ = (\frac{C B}{A B}) (A B) \\ = C B \end{aligned}$
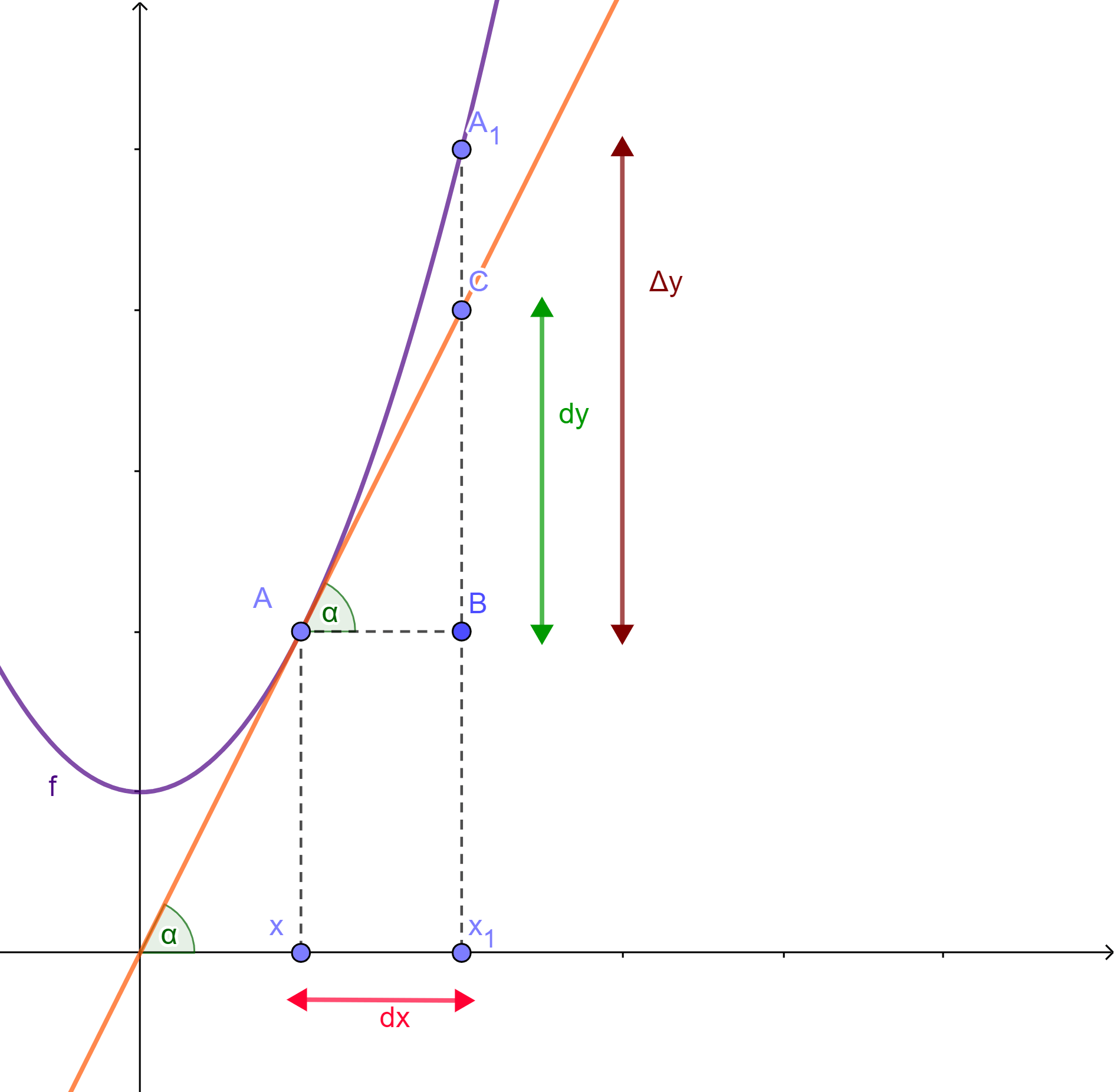
Observamos que $d y$ nos brinda una aproximación al incremento $Δ y$ que está dado por el segmento $A_{1} B$ , cuando $d x$ es pequeña.

Es decir:
$d y \approx Δ y .$

Utilizaremos esta cualidad cuando necesitemos hallar un valor aproximado del incremento de una función. En las siguientes secciones, revisaremos un par de problemas donde haremos uso de la diferencial para resolverlos.

Problema 1

Obtener el incremento del área de un cuadrado de lado $8 m$ al aumentar el lado $5 m m$ .
Para resolver este problema veremos dos métodos de solución, en el primero no usaremos la diferencial y en el segundo si la utilizaremos.

Solución sin usar la diferencial

Sabemos del problema que:
$\begin{aligned} I & = 8 m & Δ l & = 5 m m \\ A & = 64 m^{2} & l_{0} & = 8.005 m \end{aligned}$
Por lo que el área del nuevo cuadrado con el lado $l_{0}$ sería:
$\begin{aligned} A_{0} & = (8.005 m)^{2} \\ = 64.080025 m^{2} \end{aligned}$

Obtenemos el incremento del área $Δ A$ haciendo la resta del área original con el área del nuevo cuadrado.
$\begin{aligned} Δ A & = 64.080025 m^{2} - 64 m^{2} \\ = 0.080025 m^{2} \end{aligned}$

$∴ Δ A = 0.080025 m^{2} .$

Solución utilizando la diferencial

Si tomamos a $l$ como el lado del cuadrado tenemos que su área es:
$A = l^{2} .$
Como sabemos que $d A \approx Δ A$ usando la definición para la diferencial de $a$ tendríamos:
$\begin{aligned} d A & = 2 l d l \\ = 2 (8) (0.005) \\ = 0.08 \end{aligned}$
Por lo tanto tenemos que el incremento obtenido es:
$Δ A \approx 0.08 m^{2} .$

Notamos que es una buena aproximación al incremento obtenido en el método anterior. Sin embargo, al haber utilizado la diferencial, el problema nos resultó un poco más sencillo de resolver.

Problema 2

Si sabemos que $\sqrt{25} = 5$ , obtén una aproximación al valor $\sqrt{27}$ .
Solución:
Consideraremos la función $y = \sqrt{x}$ . Del problema podemos ver que el incremento de $x$ es:
$Δ x = 27 - 25 = 2$

Ahora obtengamos la diferencial de $y$ :
$d y = \frac{d y}{2 \sqrt{x}} (* *)$

Nosotros consideraremos a $x = 25$ y como una aproximación al diferencial de $x$ al incremento $Δ x = 2$ . Entonces ocurre que al sustituir todo en $(* *)$ tenemos:
$\begin{aligned} d y & = \frac{2}{2 \sqrt{25}} \\ = \frac{2}{(2) (5)} \\ = \frac{1}{5} \\ = 0.2 \end{aligned}$
Concluimos así que una aproximación al valor de $\sqrt{27}$ es:
$\begin{aligned} \sqrt{27} & \approx 5 + 0.2 \\ \approx 5.2 \end{aligned}$
$∴ \sqrt{27} \approx 5.2$
Si comparamos esta aproximación con el valor que nos brinda una calculadora $\sqrt{27} = 5.1961$ considerando sólo cuatro decimales) podemos notar que es bastante similar.

En la siguiente sección encontrarás ejercicios que podrás realizar para aplicar lo estudiado en esta entrada.

Más adelante

¡Te felicitamos por concluir con el curso de Cálculo Diferencial e Integral I! Con este tema cerramos el temario. Esperamos que hayas disfrutado este viaje por el mundo del Cálculo. Te invitamos a continuar con tu estudio ahora con el curso de Cálculo Diferencial e Integral II que se encuentra disponible en la siguiente página.

Tarea moral

Demuestra usando la definición, las siguientes reglas para las diferenciales:
- $d (s + t) = d s + d t$
- Con $c$ una constante:
  $d (c u) = c \cdot d u$
- $d (s t) = s d t + t d s$
Hallar la diferencial de las siguientes funciones:
- $y = \sqrt{1 - 4 x}$
- $t = \sin 2 s$
- $u = \log c v$
Sabiendo que $\sqrt{16} = 4$ utilizando la diferencial obtén una aproximación de $\sqrt{17}$ .
Utilizando la diferencial da una aproximación del incremento del volumen de un cubo con $l = 3 m$ al aumentar el lado $0.002 m$ .

Entradas relacionadas

Ir a: Cálculo Diferencial e Integral I
Entrada anterior del curso: Cálculo Diferencial e Integral I: Aplicaciones en economía.
Resto de cursos: Cursos

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Cálculo Diferencial e Integral I: Aplicaciones en economía

Por Karen González Cárdenas

Deja un comentario

Introducción

Imaginemos que una empresa refresquera produce $x$ botellas de bebida hidratante en total y que $a$ es el precio de venta de cada una de ellas. Si nos pidieran obtener el ingreso bastaría considerar el producto:
$a x .$
Por lo que la función de ingreso para $x$ número de unidades producidas está definida como:
$I (x) = a x .$

Ahora si consideramos que el precio de venta al público tiene una dependencia lineal con las unidades producidas. Es decir, si tomamos $a = b x + c$ una recta, tenemos que la función de ingreso $I_{1} (x)$ es:
$\begin{aligned} I_{1} (x) & = (b x + c) x \\ = b x^{2} + c x \end{aligned}$

Observamos así que la función $I_{1} (x)$ es una parábola.

Si la empresa refresquera sabe que el costo por producir $x$ botellas de bebida hidratante está dado por la función $C (x)$ , la función que nos daría el costo medio de cada botella es:

$C_{m} (x) = \frac{C (x)}{x}, con x > 0.$

Además si queremos obtener la función que nos daría su utilidad, bastaría con restarle a los ingresos los costos de producción:
$U (x) = I (x) - C (x), con x \geq 0.$

Ya que hemos visto una idea general de las funciones que utilizaremos para resolver los problemas de carácter económico de esta entrada. Comencemos con ejemplos donde se nos pide realizar la optimización de dichas funciones, para concluir revisando los conceptos: Costo marginal, Ingreso marginal y Utilidad marginal.

Problema 1

Una pequeña compañía de alimentos conoce que las funciones de ingreso y costo (en pesos) de su famosa mermelada son:
$\begin{aligned} I (x) & = - 4 x^{2} + 400 x & C (x) & = x^{2} + 20 x + 12 \end{aligned}$
Donde $x$ representa los frascos fabricados.

Te solicitan encontrar:

El costo fijo de producción.
El ingreso máximo.
La máxima utilidad.
El costo medio de cada frasco.

Solución:

$1.$ El costo fijo de producción

Ya que el costo fijo de producción es aquel que permanece constante sin importar del volumen de producción, para obtenerlo bastará con evaluar la función $C (x)$ cuando no se produce ningún frasco, es decir, cuando $x = 0$ :
$\begin{aligned} C (0) & = 0^{2} + 20 (0) + 12 \\ = 12 \end{aligned}$
Por lo que el costo fijo de producción para esta mermelada es de $12$ pesos.

$2.$ El ingreso máximo

Como nos están solicitando encontrar el ingreso máximo, aplicaremos el análisis para hallar el máximo de la función $I (x)$ apoyándonos del Criterio de la segunda derivada. Comenzamos obteniendo la primera derivada e igualando a cero para obtener los puntos críticos:
$I^{'} (x) = - 8 x + 400.$
$\begin{aligned} I^{'} (x) = 0 & \Leftrightarrow 8 x = 400 \\ \Leftrightarrow x = \frac{400}{8} \\ \Leftrightarrow x = 50 \end{aligned}$
Queremos ver que $x = 50$ , al obtener la segunda derivada notamos que:
$\begin{matrix} (que es menor que 0) & I^{''} (x) = - 8 \end{matrix}$
Concluyendo así que cuando $x = 50$ la función $I$ tiene un máximo y que el ingreso máximo de esta mermelada se obtiene al sustituir dicho valor:
$\begin{aligned} I (50) & = - 4 (50)^{2} + 400 (50) \\ = - 10000 + 20000 \\ = 10000 \end{aligned}$
Por lo que es de $10, 000$ pesos.

$3.$ La máxima utilidad

Primero necesitamos definir a la función de la utilidad, para ello usaremos la igualdad siguiente sustituyendo la función del ingreso y la del costo:
$\begin{aligned} U (x) & = I (x) - C (x) \\ = - 4 x^{2} + 400 - x^{2} - 20 x - 12 \\ = - 5 x^{2} + 388 x - 12 \\ ∴ U (x) & = 5 x^{2} + 388 x - 12 . \end{aligned}$

Derivamos la función $U$ :
$U^{'} (x) = - 10 x + 388.$
La igualamos a cero y obtenemos los puntos críticos:
$\begin{aligned} - 10 x + 388 = 0 & \Leftrightarrow 388 = 10 x \\ \Leftrightarrow x = \frac{388}{10} \end{aligned}$
Al volver a derivar la función vemos que:
$\begin{matrix} (que es negativo) & U^{''} (x) = - 10 \end{matrix}$
por lo que aplicando el Criterio de la segunda derivada nos indica que $U$ tiene un máximo cuando $x = \frac{388}{10}$ .

Sustituimos el valor para $x$ obtenido en la función:
$\begin{aligned} U (\frac{388}{10}) & = - 5 {(\frac{388}{10})}^{2} + 388 (\frac{388}{10}) - 12 \\ \approx 7515.2 \end{aligned}$
Concluyendo así que la utilidad máxima es de $7, 515.2$ pesos.

$4.$ El costo medio de cada frasco

Obtengamos la función de costo medio:
$\begin{aligned} C_{m} (x) & = \frac{C (x)}{x} \\ = \frac{x^{2} + 20 x + 12}{x} \\ ∴ C_{m} (x) & = x + 20 + \frac{12}{x} . \end{aligned}$
Del mismo modo que en los incisos anteriores, debemos derivar la función:
$C_{m}^{'} (x) = 1 - \frac{12}{x^{2}} .$
Y analizar los valores que obtengamos al igualar la derivada a cero:
$\begin{aligned} C_{m} (x) = 0 & \Leftrightarrow 1 = \frac{12}{x^{2}} \\ \Leftrightarrow \frac{1}{12} = \frac{1}{x^{2}} \\ \Leftrightarrow 12 = x^{2} \\ ∴ x = \sqrt{12} . \end{aligned}$
Queremos ver que el valor $x = \sqrt{12}$ es un mínimo para la función del costo medio, aplicando el criterio:
$C_{m}^{''} (x) = \frac{24}{x^{3}} .$
Debido a que $C_{m} (\sqrt{12}) > 0$ confirmamos que se trata de un mínimo. Finalmente sustituimos:
$\begin{aligned} C_{m} (\sqrt{12}) & = \sqrt{12} + 20 + \frac{12}{\sqrt{12}} \\ \approx 26.92 \end{aligned}$

En resumen, el costo medio de cada frasco es de $26.92$ pesos.

Hablemos del costo marginal

Recordemos un poco lo visto en la entrada Razón de cambio aplicándolo ahora a la función del costo $C (x)$ . Imaginemos que la compañía decide aumentar el número de artículos producidos de $x_{1}$ a $x_{2}$ , por lo que el costo tendría un incremento de $C (x_{1})$ a $C (x_{2})$ . Con lo anterior, la razón de cambio del costo quedaría:
$\begin{aligned} \frac{Δ C}{Δ x} & = \frac{C (x_{2}) - C (x_{1})}{x_{2} - x_{1}} . \end{aligned}$

Cabe aclarar que escribimos $Δ x = x_{2} - x_{1}$ para referimos al «incremento de $x$ ».

Observación: Como sabemos que $x_{1} < x_{2}$ , una forma de reescribir a $x_{2}$ haciendo uso de la notación anterior sería:
$x_{2} = x_{1} + Δ x .$

Por lo que concluimos que:
$\begin{aligned} \frac{Δ C}{Δ x} & = \frac{C (x_{1} + Δ x) - C (x_{1})}{Δ x} . \end{aligned}$

Si consideramos el límite cuando el incremento $Δ x \to 0$ , es decir,
$lim_{Δ x \to 0} \frac{C (x_{1} + Δ x) - C (x_{1})}{Δ x} .$

vemos que es justo la derivada de la función $C (x)$ por definición. En Economía a dicha derivada $C^{'} (x)$ se le conoce como Costo marginal.

Una relación entre el Costo promedio y el Costo marginal

Ya vimos que la función de costo promedio está dada por:
$C_{m} (x) = \frac{C (x)}{x} .$
¿Qué pasaría si decidimos hallar el mínimo de $C_{m} (x)$ ? Aplicando las reglas de derivación correspondientes tenemos:
$C_{m}^{'} (x) = \frac{x C^{'} (x) - C (x)}{x^{2}} .$

Procedemos a igualar la derivada a cero:
$\begin{aligned} C_{m}^{'} (x) = 0 & \Leftrightarrow \frac{x C^{'} (x) - C (x)}{x^{2}} = 0 \\ \Leftrightarrow x C^{'} (x) - C (x) = 0 \\ \Leftrightarrow x C^{'} (x) = C (x) \\ \Leftrightarrow C^{'} (x) = \frac{C (x)}{x} \end{aligned}$

Por lo que vemos que el costo marginal es igual al costo promedio siempre que verifiquemos que $x$ es un mínimo de $C_{m}$ . Esta relación es quizás una de las más interesantes, revisemos como utilizarla en el siguiente problema.

Problema 2

Una franquicia de panaderías conoce que la función de costo por elaborar $x$ donas es:
$C (x) = \frac{x^{2}}{500} + 2 x + 3000.$

Se requiere obtener el nivel de producción para el cual el costo promedio es el más bajo.

Solución:
Como ya vimos, si queremos minimizar el costo promedio basta con igualarlo al costo marginal y verificar que el valor $x$ obtenido es un mínimo. Para ello procedemos con:
$\begin{aligned} C^{'} (x) & = \frac{x}{250} + 2 & C_{m} (x) & = \frac{x}{500} + 2 + \frac{3000}{x} \end{aligned}$

Igualando las funciones:
$\begin{aligned} C^{'} (x) = C m_{(} x) & \Rightarrow \frac{x}{250} + 2 = \frac{x}{500} + 2 + \frac{3000}{x} \\ \Rightarrow \frac{x}{250} = \frac{x}{500} + \frac{3000}{x} \\ \Rightarrow \frac{x}{500} = \frac{3000}{x} \\ \Rightarrow \frac{x^{2}}{500} = 3000 \\ \Rightarrow x^{2} = \frac{3000}{\frac{1}{500}} \\ \Rightarrow x = \sqrt{1500000} \\ ∴ x \approx 1224.7448 \end{aligned}$

Verifiquemos que $x = 1224.7448$ es un mínimo observando la segunda derivada de $C_{m} (x)$ :
$C_{m}^{'} (x) = \frac{1}{500} - \frac{3000}{x^{2}} \Rightarrow C_{m}^{''} (x) = \frac{6000}{x^{3}}$

Al evaluarla vemos que cumple ser mayor que cero $C_{m} (1224.7448) > 0$ , que sabemos nos indica que se trata de un mínimo. Por lo tanto, el nivel buscado es el de producir $1, 225$ donas con costo medio de $C_{m} (1225) = 6.89$ por pieza.

Análogamente…

Si realizamos un desarrollo similar al revisado en la sección anterior para el costo $C (x)$ aplicado ahora a las funciones de ingreso $I$ y de utilidad $U$ , tenemos que las derivadas de ellas son conocidas en Economía como:

Ingreso marginal
$I^{'} (x)$
Utilidad marginal
$U^{'} (x)$

En los ejercicios de Tarea moral se proponen algunos ejercicios donde podrás aplicar estos conceptos, al igual que los revisados durante toda la sesión.

Más adelante

Ya que hemos concluido de revisar algunas aplicaciones de la derivada relacionadas ahora en el ámbito de la Economía, en la siguiente entrada estudiaremos el último tema de nuestro temario para Cálculo Diferencial e Integral I: las diferenciales.

Tarea moral

Dadas las funciones de ingreso y costo siguientes:
$\begin{aligned} I (x) & = - x^{2} + 170 & C (x) & = \frac{3}{2} x^{2} + 300 \end{aligned}$
Obtén lo siguiente:
- El costo fijo de producción.
- El ingreso máximo.
- La máxima utilidad.
- El costo medio de cada frasco.
Con el planteamiento del Problema 1. Determina cuando se producen $20$ frascos de mermelada:
- El ingreso y el ingreso marginal.
- La utilidad y su utilidad marginal.

Entradas relacionadas

Ir a: Cálculo Diferencial e Integral I
Entrada anterior del curso: Cálculo Diferencial e Integral I: Polinomios de Taylor (Parte 2).
Entrada siguiente del curso: Cálculo Diferencial e Integral I: Diferenciales.
Resto de cursos: Cursos

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Cálculo Diferencial e Integral I: Polinomios de Taylor (Parte 2)

Por Karen González Cárdenas

Deja un comentario

Introducción

En la entrada anterior vimos que el polinomio de Taylor para una función $f$ que se puede derivar $n$ veces en $x = a$ , es:
$T_{a, n} = \sum_{j = 0}^{n} \frac{f^{(j)} (a)}{j!} (x - a)^{j} .$

Además vimos que cumplía con la siguiente igualdad:
$lim_{x \to a} \frac{f (x) - T_{a, n} (x)}{(x - a)^{n}} = 0$

que nos indicaba que el polinomio de Taylor es una buena aproximación de la función $f$ .

Pero, ¿qué podemos decir de la diferencia $f (x) - T_{a, n} (x)$ ? ¿Cuáles son las propiedades que cumple?

A lo largo de esta entrada veremos que dicha diferencia es llamada Residuo de Taylor y que existen un par de formas de escribirlo. También veremos un ejemplo donde se nos pedirá estimar dicho residuo dependiendo del polinomio de Taylor considerado.

Definición del Residuo de Taylor

Retomando uno de los ejemplos anteriores:

En esta imagen vemos que el polinomio de Taylor $T_{2, 0}$ se parece mucho a la función $f$ cuando $a = 0$ , sin embargo, sigue existiendo una diferencia o «error» ya que el polinomio y $f$ no son «idénticas». A dicho error se le conoce formalmente como Residuo de Taylor, veamos su definición:

Definición (Residuo de Taylor): Consideremos una función $f : [x_{0}, y_{0}] \to R$ de clase $C^{(n)}$ . Definiremos al Residuo de Taylor de grado $n$ con centro en $a$ como:
$R_{n, a} : [x_{0}, y_{0}] \to R$
$R_{n, a} (x) = f (x) - T_{n, a} (x) .$

Nota: Recordemos que una función es de clase $C^{(n)}$ si es $n$ veces derivable y sus $n$ derivadas son continuas.

Vemos que de la definición anterior tenemos que al realizar una aproximación usando polinomios de Taylor para una función $f$ se da la siguiente igualdad :
$f (x) = T_{n, a} (x) + R_{n, a} (x) .$

Y además si sustituimos $R_{n, a} (x) = f (x) - T_{n, a} (x)$ en el siguiente límite:
$lim_{x \to a} \frac{f (x) - T_{n, a} (x)}{(x - a)^{n}} = 0.$

Concluimos que:

$lim_{x \to a} \frac{R_{n, a} (x)}{(x - a)^{n}} = 0.$

Reescribiendo tenemos que podemos hallar al polinomio de Taylor para una función $f$ considerando:
$f (x) = T_{n, a} (x) + (x - a)^{n} R_{n, a}^{*} (x)$
donde $R_{n, a}^{*} (x) = \frac{R_{n, a} (x)}{(x - a)^{n}}$ y el residuo cuando $x$ tiende a $a$ es cero:
$lim_{x \to a} R_{n, a}^{*} (x) = 0$

¿De qué forma podemos escribir el Residuo de Taylor?

En el siguiente teorema veremos dos maneras distintas para el residuo: la de Cauchy y la de Lagrange.

Teorema: Consideremos una función $f : [x_{0}, y_{0}] \to R$ donde $f$ es $n + 1$ veces derivable en $(x_{0}, y_{0})$ , un punto $a \in [x_{0}, y_{0}]$ y un $x \in (x, y_{0}]$ . Entonces existe $t \in (a, x)$ tal que:

$R_{n, a} (x) = \frac{f^{(n + 1)} (t)}{n!} (x - t)^{n} (x - a)$
que es la forma del residuo de Cauchy.
$R_{n, a} (x) = \frac{f^{(n + 1)} (t)}{(n + 1)!} (x - a)^{n + 1}$
que es la forma del residuo de Lagrange.

Demostración: Para realizar la prueba de los dos puntos del teorema veremos primero cuál es la derivada del residuo $R_{n, t}$ . Por ello consideraremos a la función $Q : [a, x] \to R$ como sigue:
$\begin{aligned} Q (t) & = R_{n, t} (x) \\ (por definición de residuo) & = f (x) - T_{n, t} (x) \\ (por definición de Taylor) & = f (x) - \sum_{j = 0}^{n} \frac{f^{(j)} (t)}{j!} (x - t)^{j} \end{aligned}$
Cabe mencionar que estamos considerando fija a $x$ .

Observemos lo siguiente, a estos puntos los llamaremos $(*)$ :

$\begin{aligned} Q (x) & = f (x) - T_{n, x} (x) \\ = f (x) - f (x) \\ = 0 \end{aligned}$
$Q (a) = R_{n, a} (x)$

Ahora si derivamos a $Q (t)$ respecto de $t$ obtenemos:
$\begin{aligned} \frac{d Q}{d t} (t) & = 0 - \sum_{j = 0}^{n} (\frac{f^{(j + 1)} (t)}{j!} (x - t)^{j} - \frac{f^{(j)} (t)}{j!} j (x - t)^{j - 1}) \\ = - \sum_{j = 0}^{n} (\frac{f^{(j + 1)} (t)}{j!} (x - t)^{j} - \frac{f^{(j)} (t)}{(j - 1)!} (x - t)^{j - 1}) \\ = - (f^{(1)} (t) (1) - 0 + f^{(2)} (t) (x - t) - f^{(1)} (t) + \frac{f^{(3)} (t)}{2!} (x - t)^{2} - f^{(2)} (t) (x - t) + \dots + \frac{f^{(n + 1)} (t)}{n!} (x - t)^{n} - \frac{f^{(n)} (t)}{(n - 1)!} (x - t)^{n - 1}) \end{aligned}$

Observamos que los términos se van cancelando, ya que va apareciendo alternadamente positivos y negativos:
$\begin{aligned} = - (f^{(1)} (t) (1) - 0 + f^{(2)} (t) (x - t) - f^{(1)} (t) + \frac{f^{(3)} (t)}{2!} (x - t)^{2} - f^{(2)} (t) (x - t) + \dots + \frac{f^{(n + 1)} (t)}{n!} (x - t)^{n} - \frac{f^{(n)} (t)}{(n - 1)!} (x - t)^{n - 1}) \\ = - (f^{(2)} (t) (x - t) + \frac{f^{(3)} (t)}{2!} (x - t)^{2} - f^{(2)} (t) (x - t) + \dots + \frac{f^{(n + 1)} (t)}{n!} (x - t)^{n} - \frac{f^{(n)} (t)}{(n - 1)!} (x - t)^{n - 1}) \end{aligned}$

Si continuamos cancelando los términos, notamos que el único que nos queda es:
$\begin{aligned} = - \frac{f^{(n + 1)} (t)}{n!} (x - t)^{n} \end{aligned}$

Concluimos que:
$Q^{'} (t) = - \frac{f^{(n + 1)} (t)}{n!} (x - t)^{n}$
A la igualdad anterior la llamaremos $(* *)$ .

Pasemos a probar los puntos $1.$ y $2.$ :

Aplicaremos el Teorema del valor medio para la derivada en el intervalo $[a, x]$ , así tenemos que existe un $t \in [a, x]$ tal que.
$Q^{'} (t) = \frac{Q (x) - Q (a)}{x - a}$
Por las observaciones $(*)$ y $(* *)$ tendríamos la siguiente igualdad:
$- \frac{f^{(n + 1)} (t)}{n!} (x - t)^{n} = \frac{0 - R_{n, a} (x)}{x - a}$
De lo anterior, al simplificar nos queda:
$R_{n, a} (x) = \frac{f^{(n + 1)} (t)}{n!} (x - t)^{n} (x - a)$
Ahora usaremos el Teorema del valor medio generalizado o de Cauchy, si tomamos $g (t) = (x - t)^{n + 1}$ entonces existe un $t \in (a, x)$ tal que:
$\begin{aligned} (Q (x) - Q (a)) g^{'} (t) = (g (x) - g (a)) Q^{'} (t) & \Rightarrow \frac{Q (x) - Q (a)}{g (x) - g (a)} = \frac{Q^{'} (t)}{g^{'} (t)} \end{aligned}$
Así por $(* *)$ ocurre que:
$\begin{aligned} \frac{Q (x) - Q (a)}{g (x) - g (a)} & = \frac{- \frac{f^{(n + 1)} (t)}{n!} (x - t)^{n}}{- (n + 1) (x - t)^{n}} \\ = \frac{f^{(n + 1)} (t)}{n! (n + 1)} \\ = \frac{f^{(n + 1)} (t)}{(n + 1)!} \end{aligned}$
Si ahora consideramos las observaciones dadas en $(*)$ para $Q (x)$ y evaluamos $g (x)$ ocurre que:
$\begin{aligned} \frac{Q (x) - Q (a)}{g (x) - g (a)} & = \frac{0 - Q (a)}{0 - g (a)} \\ = \frac{Q (a)}{g (a)} \end{aligned}$
Finalmente tenemos que:
$\frac{Q (a)}{g (a)} = \frac{f^{(n + 1)} (t)}{(n + 1)!} \Leftrightarrow Q (a) = \frac{f^{(n + 1)} (t)}{(n + 1)!} (x - a)^{n + 1} .$
Ya que $Q (a) = R_{n, a} (x)$ concluimos:
$R_{n, a} (x) = \frac{f^{(n + 1)} (t)}{(n + 1)!} (x - a)^{n + 1} .$

Ahora que hemos terminado la demostración, para los ejercicios que veremos a continuación podremos utilizar la forma del residuo que más nos convenga.

Ejercicios

Consideremos la función $f (x) = e^{x}$ en $a = 0$ . Estima el error de la aproximación del polinomio de Taylor de grado $2$ para $x = \frac{1}{2}$ .

Solución:
Primero obtengamos el Residuo de $f$ utilizando la forma de Lagrange:
$\begin{aligned} R_{2, 0} (\frac{1}{2}) & = \frac{f^{(2 + 1)} (t)}{(2 + 1)!} {(\frac{1}{2} - 0)}^{2 + 1} \\ = \frac{f^{(3)} (t)}{3!} {(\frac{1}{2})}^{3} \end{aligned}$

Como la tercera derivada de $f (t)$ es $e^{t}$ , sustituyendo nos queda:
$\begin{aligned} = \frac{e^{t}}{3!} {(\frac{1}{2})}^{3} \\ = \frac{e^{t}}{6} (\frac{1}{8}) \\ = \frac{e^{t}}{48} \end{aligned}$

Del Teorema que vimos, sabemos que $t \in (0, \frac{1}{2})$ por lo que se cumple la desigualdad:
$\frac{e^{t}}{48} < \frac{\sqrt{e}}{48} .$
Observemos además que el valor de $e^{t}$ se encuentra dentro del intervalo:
$(e^{0}, e^{\frac{1}{2}}) = (1, \sqrt{e}) .$

Así concluimos que el Residuo está acotado por el valor:
$\frac{\sqrt{e^{t}}}{48} \approx 0.034$
$∴ R_{2, 0} < 0.034$

De este modo el polinomio de Taylor $T_{2, 0} (\frac{1}{2})$ de grado $2$ con centro en $0$ para el valor $x = \frac{1}{2}$ aproxima a $f (\frac{1}{2}) = \sqrt{e}$ con un error menor que $0.034$ .

Brinda una aproximación del valor $\sqrt[3]{e^{2}}$ con un error menor a $10^{- 4}$ .

Solución:
Para resolver este problema vamos a considerar lo siguiente:
$\begin{aligned} f (x) & = e^{x} & a & = 0 & x & = \frac{2}{3} \end{aligned}$

Observamos que en este caso no sabemos cuál es el valor $n$ del grado del polinomio de Taylor, esta variable $n$ es justo la que queremos encontrar. Comenzamos escribiendo el Residuo de Taylor en la forma de Lagrange sustituyendo los valores que sí conocemos:
$\begin{aligned} R_{n, 0} (\frac{2}{3}) & = \frac{f^{(n + 1)} (t)}{(n + 1)!} {(\frac{2}{3} - 0)}^{n + 1} \\ (por f^{(n + 1)} (t) = e^{t}) & = \frac{e^{t}}{(n + 1)!} (\frac{2}{3})^{n + 1}) \end{aligned}$

Como $t \in (0, \frac{2}{3})$ tenemos la desigualdad:
$\frac{e^{t}}{(n + 1)!} {(\frac{2}{3})}^{n + 1} < \frac{e^{\frac{2}{3}}}{(n + 1)!} {(\frac{2}{3})}^{n + 1}$
Donde $\frac{e^{\frac{2}{3}}}{(n + 1)!} {(\frac{2}{3})}^{n + 1}$ cumple:
$\frac{e^{t}}{(n + 1)!} {(\frac{2}{3})}^{n + 1} < \frac{e^{\frac{2}{3}}}{(n + 1)!} {(\frac{2}{3})}^{n + 1} < \frac{e}{(n + 1)!}$
Además como $\frac{e}{(n + 1)!}$ es menor que $\frac{3}{(n + 1)!}$ :
$\frac{e^{t}}{(n + 1)!} {(\frac{2}{3})}^{n + 1} < \frac{e^{\frac{2}{3}}}{(n + 1)!} {(\frac{2}{3})}^{n + 1} < \frac{e}{(n + 1)!} < \frac{3}{(n + 1)!}$

Así por la transitividad de las desigualdades tenemos que el Residuo cumple:
$R_{n, 0} < \frac{3}{(n + 1)!} .$

Sin embargo nos piden que el error sea menor que $10^{- 4}$ , por lo que necesitamos estudiar la desigualdad:
$\frac{3}{(n + 1)!} < \frac{1}{10^{4}} .$

Si reescribimos la desigualdad anterior:
$\begin{aligned} \frac{3}{(n + 1)!} < \frac{1}{10^{4}} & \Leftrightarrow (3) (10^{4}) < (n + 1)! \\ \Leftrightarrow 30000 < (n + 1)! \end{aligned}$

Ahora debemos pensar en un valor $n + 1 \in N$ cuyo factorial cumpla con ser mayor que $30000$ , veamos una lista:

$\begin{aligned} 1! & = 1 \\ 2! & = 2 \\ 3! & = 6 \\ 4! & = 24 \\ 5! & = 120 \\ 6! & = 720 \\ 7! & = 5040 \\ 8! & = 40320 \end{aligned}$

Vemos que si $n + 1 = 8$ ya logramos cumplir con la desigualdad, por lo que cuando consideramos el grado del Polinomio de Taylor $n = 7$ para el valor $x = \frac{2}{3}$ cumplimos con que el error es menor a $10^{- 4}$ .

En la sección de Tarea moral te dejaremos algunos ejercicios que ayudarán a practicar lo estudiado en esta entrada.

Más adelante

Por el momento hemos terminado de revisar los temas concernientes a los polinomios de Taylor para este curso. En Cálculo Diferencial e Integral II revisarás algunos otros resultados. Para la próxima entrada, veremos algunas aplicaciones del Cálculo en el ámbito de la Economía.

Tarea moral

Realiza el ejercicio $1$ utilizando la forma de Cauchy para el residuo.
Para la función:
$g (x) = x \log (1 + x) .$
- Obtén el polinomio de Taylor de grado $n$ con $a = 0$ .
- Obtén el Residuo de Taylor utilizando la forma de Lagrange.
- Da una cota para el error al querer aproximar $10 \log (\frac{11}{10})$ al utilizar el polinomio de Taylor de grado $3$ .

Entradas relacionadas

Ir a: Cálculo Diferencial e Integral I
Entrada anterior del curso: Cálculo Diferencial e Integral I: Polinomios de Taylor (Parte 1).
Entrada siguiente del curso: Cálculo Diferencial e Integral I: Aplicaciones en economía.
Resto de cursos: Cursos

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Cálculo Diferencial e Integral I: Polinomios de Taylor (Parte 1)

Por Karen González Cárdenas

Deja un comentario

Introducción

Recordemos que una función polinómica $p$ es de la forma:
$p (x) = a_{0} + a_{1} x + \dots + a_{n} x^{n}$
donde vemos que es fácil calcular el valor de $p$ para cualquier valor de $x$ . Desafortunadamente, esto no es así con funciones como:
$\begin{aligned} f (x) & = \sin (x) & g (x) & = \log (x) & h (x) & = e^{x} \end{aligned}$

En esta entrada estudiaremos algunos resultados que nos ayudarán a encontrar polinomios que sean buenas aproximaciones a funciones como $f$ , $g$ y $h$ .

Revisitando a los polinomios

Si tenemos un polinomio:
$p (x) = a_{0} + a_{1} x + \dots + a_{n} x^{n}$
vemos que los coeficientes $a_{i}$ los podemos reescribir en términos de $p (x)$ y de sus derivadas en cero:
$a_{0} = p (0) .$
Observación: Consideramos a la «derivada cero de $p$ » como la función original.
$p^{'} (x) = a_{1} + 2 a_{2} x + \dots + n a_{n} x^{n - 1} \Rightarrow a_{1} = p^{'} (0)$
$\begin{aligned} p^{''} (x) = 2 a_{2} + \dots + n (n - 1) a_{n} x^{n - 2} & \Rightarrow 2 a_{2} = p^{''} (0) \\ \Rightarrow a_{2} = \frac{p^{''} (0)}{2} \end{aligned}$

Si continuamos con este procedimiento vemos que para el k-ésimo coeficiente ocurre que:
$p^{k} (x) = k! \cdot a_{k} \Rightarrow a_{k} = \frac{p^{(k)} (0)}{k!}$

Observaciones:

Consideramos $0! = 1$ y recordemos que k factorial se define como:
$k! = 1 \cdot 2 \cdot \dots \cdot (k - 1) \cdot k$
Así $6! = 1 \cdot 2 \cdot 3 \cdot 4 \cdot 5 \cdot 6 = 720$ .
Usaremos $p^{(k)} (0)$ para referirnos a la k-ésima derivada del polinomio en cero. Por lo que:
$p^{(0)} (0) = p (0)$
$a_{k}$ está bien definido cuando $k = 0$

Usando un desarrollo similar ahora para un polinomio de la forma:
$p (x) = a_{0} + a_{1} (x - a) + a_{2} (x - a)^{2} + \dots + a_{n} (x - a)^{n}$
donde estamos reemplazando las potencias de $x$ por potencias de $x - a$ .

Vemos que sus coeficientes $a_{i}$ en términos de $p$ en $a$ serían:
$a_{0} = p (0)$
$p^{(1)} (x) = a_{1} + 2 a_{2} (x - a) + \dots + n a_{n} (x - a)^{n - 1} \Rightarrow a_{1} = p^{(1)} (a)$
$\begin{aligned} p^{(2)} (x) = 2 a_{2} + \dots + (n - 1) (n) a_{n} (x - a)^{n - 2} & \Rightarrow 2 a_{2} = p^{(2)} (a) \\ \Rightarrow a_{2} = \frac{p^{(2)} (a)}{2} \end{aligned}$
$\begin{aligned} p^{(3)} (x) = 6 a_{3} + \dots + (n - 2) (n - 1) (n) a_{n} (x - a)^{n - 3} & \Rightarrow 6 a_{3} = p^{(3)} (a) \\ \Rightarrow a_{3} = \frac{p^{(3)} (a)}{6} \end{aligned}$
$⋮$
Concluimos que:
$a_{k} = \frac{p^{(k)} (a)}{k!}$

Generalizando aún más…

Para generalizar más el planteamiento anterior, tomemos ahora una función $f$ que tiene sus $n$ derivadas en $a$ :
$f^{(1)} (a), \dots, f^{(n)} (a) .$

Tenemos que los coeficientes $a_{i}$ en términos de $f (a)$ están dados por:
$a_{k} = \frac{f^{(k)} (a)}{k!}$
con $0 \leq k \leq n$ .

Así definimos:
$T_{n, a} (x) = a_{0} + a_{1} (x - a) + \dots + a_{n} (x - a)^{n}$
al polinomio de Taylor de grado $n$ de la función $f$ en $a$ .
Por lo que:
$T_{n, a}^{(k)} (a) = f^{(k)} (a), 0 \leq k \leq n .$

Definición de polinomio de Taylor

Definición (Polinomio de Taylor): Sea $f : (x_{0}, y_{0}) \to R$ , $a \in (x_{0}, y_{0})$ con $f$ n-veces derivable en $a$ . El polinomio de Taylor para $f$ con centro en $a$ de grado $n$ se define como:
$T_{n, a} (x) = \sum_{j = 0}^{n} \frac{f^{(j)} (a)}{j!} (x - a)^{j}$
donde $f^{(0)} (a) = f (a)$ .

¿Es una buena aproximación?

Ya que hemos definido al polinomio de Taylor para una función $f$ , queremos saber si éste es una buena aproximación. Para ello veamos la demostración del siguiente teorema:

Teorema: Sea $f : (x_{0}, y_{0}) \to R$ , $a \in (x_{0}, y_{0})$ tal que $f$ es de clase $C^{(n)}$ en $a \Rightarrow$ existe el polinomio de Taylor $T_{n, a}$ con:
$a_{k} = \frac{f^{k} (a)}{k!}, 0 \leq k \leq n$
que cumple con que:
$lim_{x \to a} \frac{f (x) - T_{n, a} (x)}{(x - a)^{n}} = 0$

Demostración: Iniciemos sustituyendo por definición a $T_{n, a} (x)$
$\begin{aligned} \frac{f (x) - T_{n, a} (x)}{(x - a)^{n}} & = \frac{f (x) - \sum_{j = 0}^{n} \frac{f^{(j)} (a)}{j!} (x - a)^{j}}{(x - a)^{n}} \\ = \frac{f (x) - \sum_{j = 0}^{n - 1} \frac{f^{(j)} (a)}{j!} (x - a)^{j}}{(x - a)^{n}} - \frac{\frac{f^{(n)} (a)}{n!} (x - a)^{n}}{(x - a)^{n}} \\ = \frac{f (x) - \sum_{j = 0}^{n - 1} \frac{f^{(j)} (a)}{j!} (x - a)^{j}}{(x - a)^{n}} - \frac{f^{(n)} (a)}{n!} \end{aligned}$

Para facilitar un poco la redacción consideremos a:
$\begin{aligned} S (x) & = \sum_{j = 0}^{n - 1} \frac{f^{(j)} (a)}{j!} (x - a)^{j} \\ h (x) & = (x - a)^{n} \end{aligned}$

Por lo que tenemos:
$\frac{f (x) - S (x)}{h (x)} - \frac{f^{(n)} (a)}{n!} .$

Probemos que el límite cuando $x$ tiende a $a$ es cero:
$lim_{x \to a} \frac{f (x) - S (x)}{h (x)} - \frac{f^{(n)} (a)}{n!} = 0.$

Que es equivalente a probar que:
$lim_{x \to a} \frac{f (x) - S (x)}{h (x)} = \frac{f^{(n)} (a)}{n!} .$
Observemos que para $h$ se tiene en sus derivadas los siguiente:
$\begin{aligned} h^{(0)} (x) & = (x - a)^{n} = \frac{n! (x - a)^{n - 0}}{(n - 0)!} \\ h^{(1)} (x) & = n (x - a)^{n - 1} = \frac{n! (x - a)^{n - 1}}{(n - 1)!} \\ h^{(2)} (x) & = n (n - 1) (x - a)^{n - 2} = \frac{n! (x - a)^{n - 2}}{(n - 2)!} \end{aligned}$
$⋮$
$h^{(k)} (x) = \frac{n! (x - a)^{n - k}}{(n - k)!}$

Y para $S (x)$ vemos que sus derivadas en $a$ son:
$\begin{aligned} S (x) & = a_{0} + a_{1} (x - a) + a_{2} (x - a)^{2} + \dots + a_{n - 1} (x - a)^{n - 1} \\ \Rightarrow S (a) = a_{0} \\ S^{(1)} (x) & = a_{1} + 2 a_{2} (x - a) + \dots + (n - 1) a_{n - 1} (x - a)^{n - 2} \\ \Rightarrow S^{(1)} (a) = a_{1} \\ S^{(2)} (x) & = 2 a_{2} + \dots + (n - 1) (n - 2) a_{n - 1} (x - a)^{n - 3} \\ \Rightarrow S^{(2)} (a) = 2 a_{3} \end{aligned}$
$⋮$

Reescribiendo los $a_{i}$ obtenemos:
$\begin{aligned} S^{(0)} (a) & = \frac{f^{(0)} (a)}{0!} = f^{(0)} (a) \\ S^{(1)} (a) & = \frac{f^{(1)} (a)}{1!} = f^{(1)} (a) \\ S^{(2)} (a) & = \frac{f^{(2)} (a)}{2!} (2) = f^{(2)} (a) \end{aligned}$

$⋮$

$\begin{aligned} S^{(k)} (a) & = \frac{f^{(k)} (a)}{k!} (k!) = f^{(k)} (a) \end{aligned}$

De este modo al considerar los límites:
$\begin{aligned} lim_{x \to a} (f (x) - S (x)) & = f (a) - S (a) = 0 \\ lim_{x \to a} (f^{(1)} (x) - S^{(1)} (x)) & = f^{(1)} (a) - S^{(1)} (a) = 0 \end{aligned}$
$⋮$
$\begin{aligned} lim_{x \to a} (f^{(n - 2)} (x) - S^{(n - 2)} (x)) & = 0 \end{aligned}$

Y los límites para $h$ :
$\begin{aligned} lim_{x \to a} h (x) & = g (a) = (a - a)^{n} = 0 \\ lim_{x \to a} h^{(1)} (x) & = g^{(1)} (a) = \frac{n! (a - a)^{n - 1}}{(n - 1)!} = 0 \end{aligned}$
$⋮$
$\begin{aligned} lim_{x \to a} h^{(n - 2)} (x) & = g^{(n - 2)} (a) = 0 \end{aligned}$
Del análisis anterior notamos que podemos aplicar la Regla de L’Hôpital que nos decía que teniendo que: $lim_{x \to a^{+}} f (x) = 0 = lim_{x \to a^{+}} g (x) .$

Si $lim_{x \to a^{+}} \frac{f^{'} (x)}{g^{'} (x)} = L \in R$ , entonces $lim_{x \to a^{+}} \frac{f (x)}{g (x)} = L$ .

Así al hacerlo $n - 1$ veces en el siguiente límite se da la igualdad:
$\begin{aligned} lim_{x \to a} \frac{f (x) - S (x)}{(x - a)^{n}} & = lim_{x \to a} \frac{f^{(n - 1)} (x) - S^{(n - 1)} (x)}{\frac{n! (x - a)^{n - n + 1}}{(n - n + 1)!}} \\ = lim_{x \to a} \frac{f^{(n - 1)} (x) - S^{(n - 1)} (x)}{\frac{n! (x - a)}{(1)!}} \\ = lim_{x \to a} \frac{f^{(n - 1)} (x) - S^{(n - 1)} (x)}{n! (x - a)} \end{aligned}$

Recordemos que $S (x)$ es un polinomio de grado $n - 1$ por lo que al haberlo derivado $n - 1$ veces lo que obtenemos para $S^{(n - 1)} (x)$ es una constante que resulta ser:
$S^{(n - 1)} (x) = f^{(n - 1)} (a) .$

Sustituyendo en el límite:
$\begin{aligned} lim_{x \to a} \frac{f^{(n - 1)} (x) - S^{(n - 1)} (x)}{n! (x - a)} & = lim_{x \to a} \frac{f^{(n - 1)} (x) - f^{(n - 1)} (a)}{n! (x - a)} \\ = \frac{1}{n!} (lim_{x \to a} \frac{f^{(n - 1)} (x) - f^{(n - 1)} (a)}{x - a}) \end{aligned}$

De este modo el límite resultante es por definición la n-ésima derivada de $f$ en $a$ , es decir:
$lim_{x \to a} \frac{f^{(n - 1)} (x) - f^{(n - 1)} (a)}{x - a} = f^{(n)} (a) .$

Consecuentemente:
$lim_{x \to a} \frac{f (x) - S (x)}{(x - a)^{n}} = \frac{f^{(n)} (a)}{n!} .$

Con la demostración terminada podemos afirmar que los polinomios de Taylor son una buena aproximación, ahora veamos algunos ejemplos.

Ejemplo 1

Comencemos por obtener el polinomio de Taylor para la función exponencial en $a = 0$ :
$f (x) = e^{x} .$
Veamos que todas las derivadas son de la forma:
$f^{(k)} (x) = e^{x} .$
Por lo que la k-ésima derivada valuada en $a = 0$ :
$f^{(k)} (a) = e^{0} = 1.$
Sustituyendo en la definición de polinomio de Taylor tenemos:
$T_{n, a} (x) = \sum_{j = 0}^{n} \frac{1}{j!} x^{j}$
Comencemos por ver cuáles serían los polinomios de Taylor de grado $0$ , $1$ y $2$ :
$\begin{aligned} T_{0, 0} (x) & = \frac{1}{0!} \\ T_{1, 0} (x) & = \frac{1}{0!} + \frac{1}{1!} (x - 0) \\ T_{2, 0} (x) & = \frac{1}{0!} + \frac{1}{1!} (x - 0) + \frac{1}{2!} (x - 0)^{2} \end{aligned}$

Al graficar dichos polinomios notamos que entre mayor es el grado del polinomio, mejor es la aproximación a la función:

Ejemplo 2

Ahora obtendremos el polinomio de Taylor de grado $5$ con centro en $a = 0$ para:
$g (x) = \sin (x) .$

Por lo que tenemos, calculamos las primeras cinco derivadas de $g$ y las evaluamos en cero:
$\begin{aligned} g (x) & = \sin (0) = 0 \\ g^{(1)} (x) & = \cos (0) = 1 \\ g^{(2)} (x) & = - \sin (0) = 0 \\ g^{(3)} (x) & = - \cos (0) = - 1 \\ g^{(4)} (x) & = \sin (0) = 0 \\ g^{(5)} (x) & = \cos (0) = 1 \end{aligned}$

Aplicando la definición de Taylor tenemos que su polinomio sería:
$\begin{aligned} T_{5, 0} & = \frac{0}{0!} (x - 0)^{0} + \frac{1}{1!} (x - 0)^{1} + \frac{0}{2!} (x - 0)^{2} + \frac{(- 1)}{3!} (x - 0)^{3} + \frac{0}{4!} (x - 0)^{4} + \frac{1}{5!} (x - 0)^{5} \\ = x - \frac{1}{3!} x^{3} + \frac{1}{5!} x^{5} \end{aligned}$

Al graficar este polinomio $T_{5, 0} = x - \frac{1}{3!} x^{3} + \frac{1}{5!} x^{5}$ vemos lo siguiente:

Ya que hemos revisado algunos ejemplos, en la siguiente sección te dejamos una lista de funciones de las que se te pide encontrar sus respectivos polinomios de Taylor siguiendo un procedimiento análogo.

Más adelante

Ahora que vimos la definición formal de los polinomios de Taylor, que resultan ser una buena aproximación para cualquier función $f$ con las características ya especificadas y algunos ejemplos, en la siguiente entrada veremos un resultado relacionado con su residuo.

Tarea moral

Obtener el polinomio de Taylor para las siguientes funciones:

$f (x) = \tan (x)$ de grado $3$ con $a = 0$ .
$g (x) = \sin (x)$ de grado $4$ con $a = \frac{π}{6}$ .
$h (x) = e^{e^{x}}$ de grado $3$ con $a = 0$ .
$k (x) = \log (x + 1)$ de grado $4$ con $a = 0$ .
$j (x) = \cos (x)$ de grado $m$ con $a = \frac{π}{2}$ .

Entradas relacionadas

Ir a: Cálculo Diferencial e Integral I
Entrada anterior del curso: Cálculo Diferencial e Integral I: Razón de cambio.
Entrada siguiente del curso: Cálculo Diferencial e Integral I: Polinomios de Taylor (Parte 2).
Resto de cursos: Cursos

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Cálculo Diferencial e Integral I: Razón de cambio

Por Karen González Cárdenas

Deja un comentario

Introducción

Recordemos que la derivada de una función $f$ se puede escribir del siguiente modo:
$f^{'} (x) = \frac{d f (x)}{d x} .$

Si nosotros tenemos una cantidad $x$ que se encuentra en función del tiempo $t$ , haciendo uso de la derivada podemos expresar a la razón de cambio de $x$ respecto de $t$ como:
$\frac{d x}{d t} .$
De este modo, si se tiene que dicha cantidad $x$ está relacionada con una ecuación, para obtener su razón de cambio bastaría con derivarla.

Esta interpretación de la derivada nos será de utilidad para resolver los problemas que revisaremos a continuación.

Problema 1

Un círculo expande su área de manera no especificada. Se sabe que cuando el radio es de $6 c m$ , la tasa de variación del mismo respecto al tiempo es de $4 c m$ .

Encuentra la tasa de variación del área respecto al tiempo cuando el radio $6 c m$ .
Solución:
Sabemos que el área de un círculo está dada por:
$A = π r^{2} .$
Veamos que la tasa de variación del radio $r$ es:
$\frac{d r}{d t} .$

Al derivar el área $A$ respecto del tiempo $t$ tenemos:
$\frac{d A}{d t} = 2 π r \frac{d r}{d t}$
$(1)$

De los datos que nos dan en el problema sabemos que cuando el radio es de $6 c m$ , su tasa de variación:
$\frac{d r}{d t} = 4 c m .$

Sustituyendo estos valores en $(1)$ tenemos:
$\begin{aligned} \frac{d A}{d t} & = 2 π (6 c m) (4 c m) \\ = 48 π c m^{2} \end{aligned}$

Por lo que la tasa de variación buscada es:
$\frac{d A}{d t} = 48 π c m^{2} .$

Problema 2

Por la mañana, una mujer se encuentra esperando a lado de un poste el autobús que la llevará a su trabajo. Debido a la demora, ella decide caminar rumbo al metro alejándose del poste que sabemos alumbra a razón de $3 \frac{m}{s}$ . Si además sabemos que la estatura de la mujer es de $1.60 m$ y la altura del poste de $10 m$ , ¿cuál es la razón de cambio a la cual se mueve el extremo de la sombra de la mujer?

Solución:

Vemos que el problema nos dice que:
$\frac{d z}{d t} = 3 \frac{m}{s} .$
Y que queremos obtener la razón de cambio:
$\frac{d x}{d t} .$
Observamos que los siguientes triángulos son semejantes:
$△ A B C \sim △ A E D .$
Entonces tenemos la siguiente igualdad:
$\frac{10}{1.6} = \frac{x}{x - z} .$
Desarrollando lo anterior:
$\begin{aligned} 10 (x - z) = 1.6 x & \Leftrightarrow 10 x - 10 z = 1.6 x \\ \Leftrightarrow 10 x - 1.6 x = 10 z \\ \Leftrightarrow 8.4 x = 10 z \end{aligned}$

Derivando con respecto del tiempo $t$ :
$8.4 \frac{d x}{d t} = 10 \frac{d z}{d t} .$

Despejando $\frac{d x}{d t}$ :
$\frac{d x}{d t} = \frac{10}{8.4} \frac{d z}{d t} .$

Sustituyendo el valor conocido de $\frac{d z}{d t}$ :
$\begin{aligned} \frac{d x}{d t} & = \frac{25}{21} (3) \\ = \frac{25}{7} \frac{m}{s} \end{aligned}$

Por lo tanto, la razón con que se mueve el extremo de la sombra es de:
$\frac{25}{7} \frac{m}{s} .$

Problema 3

Una pelota esférica se infla a razón de $0.16 \frac{c m^{3}}{m i n}$ . ¿Cuál es su volumen cuando su radio está aumentando a razón de $0.20 \frac{c m}{m i n}$ ?

Solución:
Recordemos que el volumen de una esfera esta dado por:
$V = \frac{4}{3} π r^{3} .$
De los datos del problema sabemos lo siguiente:
$\begin{aligned} \frac{d V}{d t} & = 0.16 \frac{c m^{3}}{m i n} & \frac{d r}{d t} & = 0.20 \frac{c m}{m i n} \end{aligned}$

Derivamos el volumen $V$ respecto del tiempo y obtenemos:
$\frac{d V}{d t} = 4 π r^{2} \frac{d r}{d t} .$

Sustituyendo $\frac{d V}{d t} = 0.16$ en la igualdad anterior:
$0.16 \frac{c m^{3}}{m i n} = 4 π r^{2} \frac{d r}{d t} .$

Ahora sustituyendo el valor de la razón de cambio del radio:
$0.16 \frac{c m^{3}}{m i n} = 4 π r^{2} (0.2 \frac{c m}{m i n}) .$

Para poder obtener el valor del volumen solicitado debemos conocer el valor del radio, por lo que despejando $r$ ocurre lo siguiente:
$\begin{aligned} \frac{0.16}{0.8} \frac{c m^{2}}{π} & = r^{2} \\ \Rightarrow \frac{c m^{2}}{5 π} & = r^{2} \end{aligned}$
$∴ r = \frac{1}{\sqrt{5 π}} c m .$

Sustituyendo el valor de $r$ en el volumen tenemos que:
$\begin{aligned} V & = \frac{4}{3} π {(\frac{1}{\sqrt{5 π}})}^{3} c m^{3} \\ \approx 0.06728 c m^{3} \end{aligned}$
Concluimos que el volumen aproximado de la pelota es de $0.06728 c m^{3}$ .

Más adelante

En la próxima entrada revisaremos el tema de polinomios de Taylor. Para ello, veremos su definición formal y algunos ejemplos de su aplicación para aproximar valores de una función.

Tarea moral

En una fábrica de hielo se tiene un cubo con volumen $V = 5 m^{3}$ . Por falta de espacio, los trabajadores deben sacarlo del congelador, provocando que comience a derretirse a razón de $2 \frac{m^{3}}{s}$ , ellos se preguntan: ¿Cuál es la razón de cambio de la superficie del cubo en ese preciso instante?
Un tronco de madera cuyo largo es de $13 m$ se encuentra apoyado sobre un muro. Se te pide hallar la velocidad con la que baja el extremo superior del tronco cuando su extremo inferior dista del muro $5 m$ . Se sabe que el tronco se separa a razón de $5 \frac{m}{s}$
Un barco pesquero de $6 m$ de altura se aleja de un faro cuya altura es de $130 m$ y alumbra con una razón de $40 \frac{m}{s}$ . Determina la razón de cambio a la cual se mueve el extremo de la sombra del barco.

Entradas relacionadas

Ir a: Cálculo Diferencial e Integral I
Entrada anterior del curso: Cálculo Diferencial e Integral I: Velocidad y aceleración.
Entrada siguiente del curso: Cálculo Diferencial e Integral I: Polinomios de Taylor (Parte 1).
Resto de cursos: Cursos

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Introducción

Definición de la diferencial de una función

Algunos ejemplos de funciones y su diferencial

Una interpretación de la diferencial

Problema 1

Solución sin usar la diferencial

Solución utilizando la diferencial

Problema 2

Más adelante

Tarea moral

Entradas relacionadas

Agradecimientos

Introducción

Problema 1

1. El costo fijo de producción

2. El ingreso máximo

3. La máxima utilidad

4. El costo medio de cada frasco

Hablemos del costo marginal

Una relación entre el Costo promedio y el Costo marginal

Problema 2

Análogamente…

Más adelante

Tarea moral

Entradas relacionadas

Agradecimientos

Introducción

Definición del Residuo de Taylor

¿De qué forma podemos escribir el Residuo de Taylor?

Ejercicios

Más adelante

Tarea moral

Entradas relacionadas

Agradecimientos

Introducción

Revisitando a los polinomios

Generalizando aún más…

Definición de polinomio de Taylor

¿Es una buena aproximación?

Ejemplo 1

Ejemplo 2

Más adelante

Tarea moral

Entradas relacionadas

Agradecimientos

Introducción

Problema 1

Problema 2

Problema 3

Más adelante

Tarea moral

Entradas relacionadas

Agradecimientos

$1.$ El costo fijo de producción

$2.$ El ingreso máximo

$3.$ La máxima utilidad

$4.$ El costo medio de cada frasco