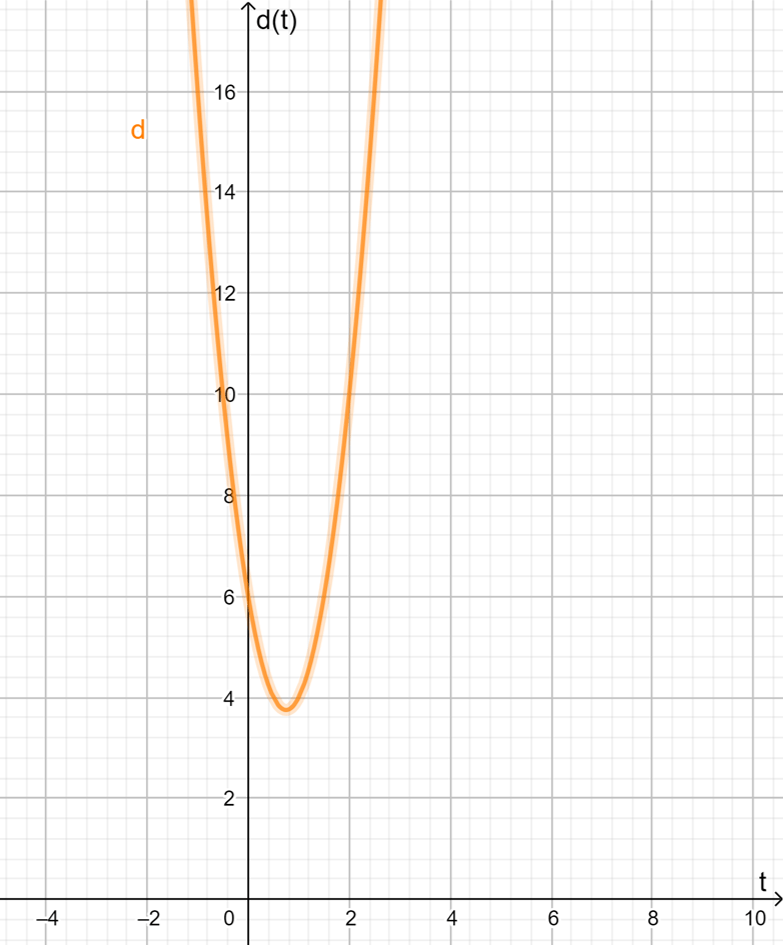Introducción
Para los problemas que veremos en esta entrada, será necesario recordar algunos conceptos de la Física relacionados con el Movimiento rectilíneo uniforme que posiblemente estudiaste en el bachillerato.
Recordemos que la velocidad se encuentra expresada por:
\begin{equation*}
v=\frac{d}{t}.
\end{equation*}
Esta igualdad modela el movimiento de un punto sobre una recta en una distancia $d$ en un tiempo $t$ con una velocidad uniforme $v$.
De la ecuación anterior podemos obtener que la distancia es:
\begin{equation}
d=v \cdot t.
\end{equation}
Ahora si consideramos a un par de puntos $(d_1,t_1)$ y $(d_2,t_2)$ tales que:
\begin{align*}
d_1&=vt_1 & d_2&=vt_2\\
\end{align*}
Así al sustituir en $(1)$ tendríamos que:
$$d_2-d_1=v(t_2-t_1) \Rightarrow v=\frac{d_2-d_1}{t_2-t_1}$$
que es justo la velocidad media.
Supongamos ahora que el movimiento ya no es de velocidad uniforme y que la función de distancia recorrida del punto $p$ en un tiempo $t$ está dada como:
$$d=d(t).$$
Por lo que ahora la función de velocidad media de $p$ en un intervalo $[t_1,t_2]$ se define como:
$$\frac{d_2-d_1}{t_2-t_1}=\frac{d(t_2)-d(t_1)}{t_2-t_1}.$$
Tomemos a $t_2-t_1=h$ por lo que tenemos las siguientes conclusiones:
- $t_2=t_1+h$ donde $h\neq 0$
- $d(t_2)= d(t_1+h)$
- $[t_1.t_2]=[t_1,t_1+h]$
En consecuencia la velocidad media queda:
$$\frac{d(t_1+h)-d(t_1)}{h}.$$
Aplicamos límite a la expresión anterior para obtener la velocidad instantánea (rapidez o sólo velocidad):
$$\lim_{h \to 0} \frac{d(t_1+h)-d(t_1)}{h}.$$
Generalizando al considerar cualquier tiempo $t$ observamos que:
$$\lim_{h \to 0} \frac{d(t+h)-d(t)}{h}=d'(t).$$
Concluyendo con la siguiente igualdad para la función velocidad de un punto $p$:
$$v(t)=d'(t).$$
Y a la aceleración media como:
$$a(t)=v'(t)=d^{‘ ‘}(t).$$
Problema 1
Supongamos que tenemos una partícula cuyo movimiento se encuentra modelado por la función:
$$d(t)=4t^{2}-6t+6$$
con la distancia expresada en metros y el tiempo en segundos.
Se nos pide encontrar:
- Su distancia recorrida cuando $t=0$.
- Su velocidad al iniciar su movimiento.
- La velocidad alcanzada transcurridos 3 segundos.
- La velocidad final a los 5 segundos.
- Su aceleración.
Solución:
- Veamos que la podemos obtener evaluando la función de movimiento cuando $t=0$:
$$d(0)= 4(0)^{2}-6(0)+6= 6m.$$ - Para la velocidad al iniciar basta derivar $d$ y evaluarla con $t=0$:
$$v(t)=d'(t)= 8t-6.$$
De este modo:
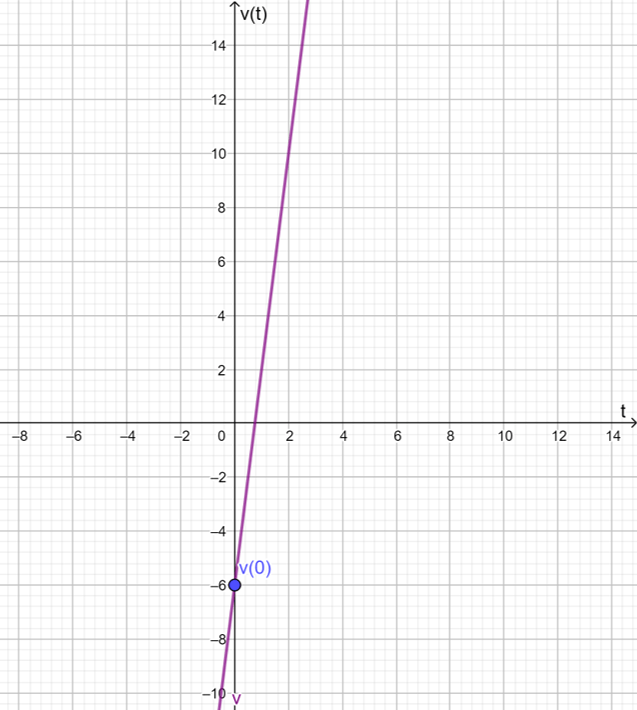
$$v(0)=-6 \frac{m}{s}.$$
Esto lo podemos ver en la gráfica de la función $v$:
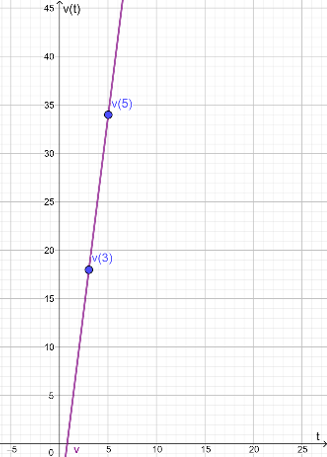
- Evaluemos la función $v$ con $t=3$:
\begin{align*}
v(3)&=8(3)-6\\
&=24-6\\
\therefore v(3)&=18 \frac{m}{s}.
\end{align*} - Ahora cuando $t=5$:
\begin{align*}
v(5)&=8(5)-6\\
&=40-6\\
\therefore v(5)&= 34\frac{m}{s}.
\end{align*}
Observamos con lo anterior que la velocidad es creciente.
- Debemos obtener la segunda derivada de la función $d$, que es equivalente a derivar la velocidad:
\begin{align*}
a(t)&=v^{‘ ‘}(t)\\
&= 8 \frac{m}{s^{2}}.
\end{align*}
Por lo que tenemos que su aceleración es constante.
Problema 2
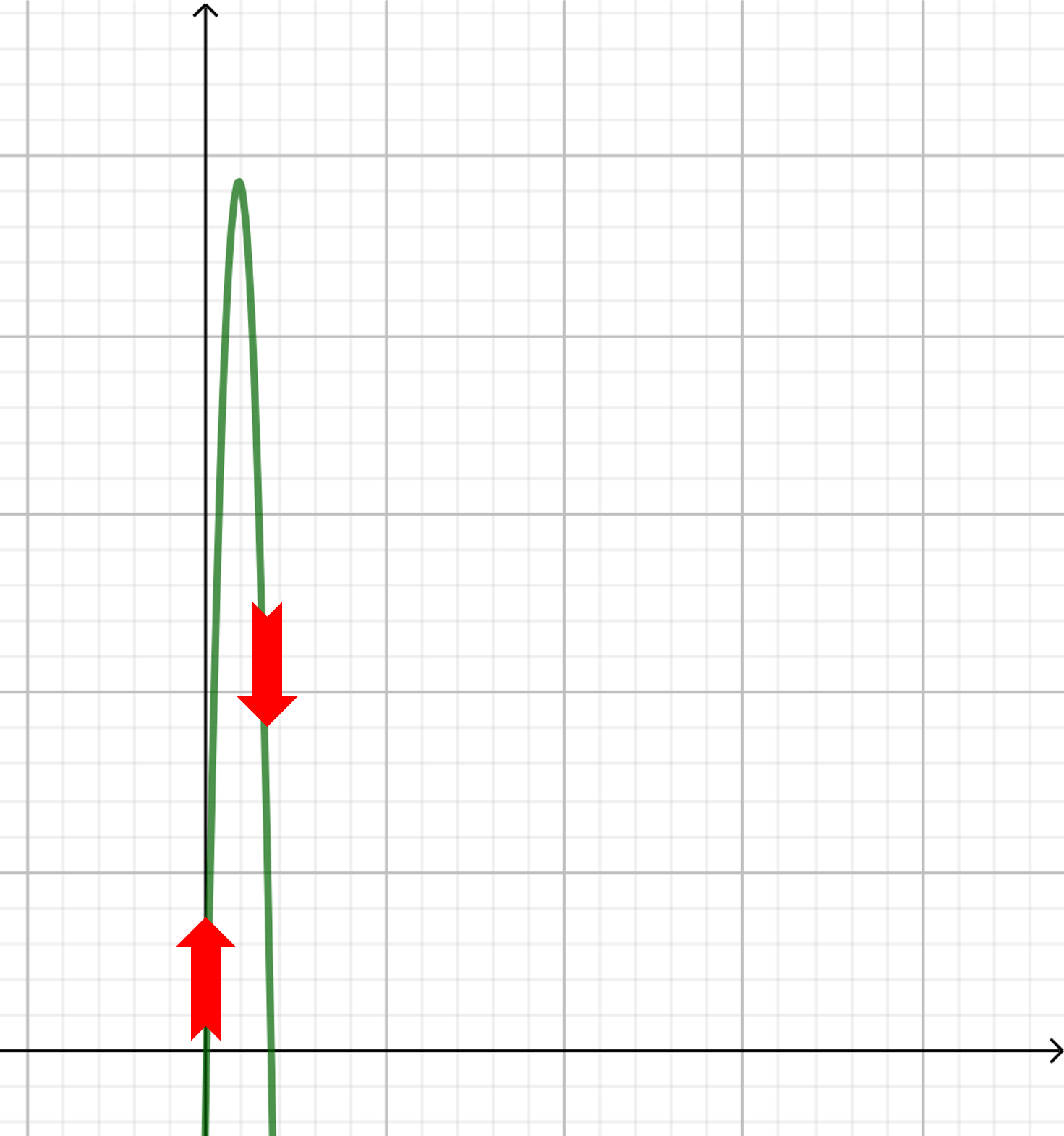
Un proyectil es lanzado, tenemos que la función que describe la altura alcanzada al tiempo $t$ es:
$$d(t)=-3t^{2}+54t$$
¿En qué instante alcanza su altura máxima y cuál es su valor?
Solución:
Comenzaremos derivando la función $d$:
$$d'(t)=-6t+54.$$
Igualamos a cero para encontrar el máximo:
\begin{align*}
d'(t)=0 &\Leftrightarrow -6t+54=0\\
&\Leftrightarrow -t+9=0\\
&\Leftrightarrow t=9
\end{align*}
Aplicando el Criterio de la segunda derivada comprobamos que se trata de un máximo cuando $t=9$:
$$d^{‘ ‘}(t)=-6 <0.$$
Así para obtener el valor de la altura basta sustituir $t=9$ en la función $d$:
\begin{align*}
d(9)&=-3(9)^{2}+54(9)\\
&=-3(81)+486\\
&=-243+486\\
&=243
\end{align*}
$\therefore$ La altura es de $243 m$.
Problema 3
Tenemos que la distancia recorrida por una partícula se expresa mediante la función:
$$d(t)=2t^{3}-5t^{2}+10t$$
donde consideramos a $d$ en metros y a $t$ en segundos.
¿Cuál es su velocidad cuando:
- $t=1$,
- $t=\frac{3}{2}$,
- $t=0$ ?
Solución:
Primero obtenemos la función velocidad derivando $d$:
$$v(t)=d'(t)=6t^{2}-10t+10.$$
Ahora evaluamos los valores que nos piden:
- Con $t=1$:
$$v(1)=6(1)^{2}-10(1)+10=6.$$
$$\therefore v(1)=6\frac{m}{s}.$$ - Con $t=\frac{3}{2}$:
$$v\left(\frac{3}{2}\right)=6\left(\frac{3}{2}\right)^{2}-10\left(\frac{3}{2}\right)+10=\frac{17}{2}.$$
$$\therefore v\left(\frac{3}{2}\right)=\frac{17}{2}\frac{m}{s}.$$ - Con $t=0$:
$$v(0)=6(0)^{2}-10(0)+10=10.$$
$$\therefore v(0)=10\frac{m}{s}.$$
Después de ver estos problemas, te dejamos a continuación una lista de ejercicios para que puedas practicar el tema visto en esta entrada.
Más adelante
En la próxima entrada, veremos que haciendo uso de la derivada podemos obtener la razón de cambio de dos o más variables relacionadas en un problema.
Tarea moral
- Una pelota es lanzada desde el suelo hacia arriba y su altura sigue la función:
$$d(t)=30t-5t^{2}.$$
Determina cuál es la altura máxima que alcanza la pelota. - La distancia recorrida por un automóvil se encuentra definida por la función:
$$m(t)=t^{2}-3t+1$$
donde estamos considerando a $m$ expresada en kilómetros y a $t$ en horas.
Se requiere obtener:- Su distancia recorrida cuando $t=0.$
- Su velocidad al iniciar su movimiento.
- La velocidad alcanzada transcurridas 2 horas.
- La velocidad final a las 6 horas.
- Su aceleración.
Entradas relacionadas
- Ir a: Cálculo Diferencial e Integral I
- Entrada anterior del curso: Cálculo Diferencial e Integral I: Problemas de optimización.
- Entrada siguiente del curso: Cálculo Diferencial e Integral I: Razón de cambio.
- Resto de cursos: Cursos
Agradecimientos
Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»