Archivo de la etiqueta: Aproximación polinómica

Cálculo Diferencial e Integral I: Polinomios de Taylor (Parte 1)

Por Karen González Cárdenas

Deja un comentario

Introducción

Recordemos que una función polinómica $p$ es de la forma:
$$p(x)=a_0+ a_1 x+ \ldots +a_n x^{n}$$
donde vemos que es fácil calcular el valor de $p$ para cualquier valor de $x$. Desafortunadamente, esto no es así con funciones como:
\begin{align*}
f(x)&= \sin(x) & g(x)&= \log(x) & h(x)&=e^{x}
\end{align*}

En esta entrada estudiaremos algunos resultados que nos ayudarán a encontrar polinomios que sean buenas aproximaciones a funciones como $f$, $g$ y $h$.

Revisitando a los polinomios

Si tenemos un polinomio:
$$p(x)=a_0+ a_1 x+ \ldots +a_n x^{n}$$
vemos que los coeficientes $a_i$ los podemos reescribir en términos de $p(x)$ y de sus derivadas en cero:
$$a_0=p(0).$$
Observación: Consideramos a la «derivada cero de $p$» como la función original.
$$p'(x)=a_1+2a_2 x+\ldots +n a_n x^{n-1} \Rightarrow a_1=p'(0)$$
\begin{align*}
p \dquote (x)=2a_2+ \ldots + n(n-1)a_nx^{n-2} &\Rightarrow 2a_2=p \dquote (0)\\
&\Rightarrow a_2=\frac{p \dquote (0)}{2}
\end{align*}

Si continuamos con este procedimiento vemos que para el k-ésimo coeficiente ocurre que:
$$p^{k}(x)=k! \cdot a_k \Rightarrow a_k=\frac{p^{(k)}(0)}{k!}$$

Observaciones:

  • Consideramos $0! =1$ y recordemos que k factorial se define como:
    $$k!= 1 \cdot 2 \cdot \ldots \cdot (k-1) \cdot k$$
    Así $6! = 1 \cdot 2 \cdot 3 \cdot 4 \cdot 5 \cdot 6 =720$.
  • Usaremos $p^{(k)}(0)$ para referirnos a la k-ésima derivada del polinomio en cero. Por lo que:
    $$p^{(0)}(0)=p(0)$$
  • $a_k$ está bien definido cuando $k=0$

Usando un desarrollo similar ahora para un polinomio de la forma:
$$p(x)=a_0+ a_1 (x-a)+a_2 (x-a)^{2}+ \ldots +a_n (x-a)^{n}$$
donde estamos reemplazando las potencias de $x$ por potencias de $x-a$.

Vemos que sus coeficientes $a_i$ en términos de $p$ en $a$ serían:
$$a_0=p(0)$$
$$p^{(1)}(x)=a_1+2a_2(x-a)+\ldots + n a_n (x-a)^{n-1} \Rightarrow a_1= p^{(1)} (a)$$
\begin{align*}
p^{(2)}(x)=2a_2+ \ldots +(n-1)(n) a_n (x-a)^{n-2} &\Rightarrow 2a_2 = p^{(2)}(a)\\
&\Rightarrow a_2 = \frac{p^{(2)}(a)}{2}
\end{align*}
\begin{align*}
p^{(3)}(x)= 6 a_3+ \ldots + (n-2)(n-1)(n)a_n(x-a)^{n-3} &\Rightarrow 6a_3 = p^{(3)}(a)\\
&\Rightarrow a_3 =\frac{ p^{(3)}(a)}{6}
\end{align*}
$$\vdots$$
Concluimos que:
$$a_k=\frac{p^{(k)}(a)}{k!}$$

Generalizando aún más…

Para generalizar más el planteamiento anterior, tomemos ahora una función $f$ que tiene sus $n$ derivadas en $a$:
$$f^{(1)}(a), \ldots , f^{(n)}(a).$$

Tenemos que los coeficientes $a_i$ en términos de $f(a)$ están dados por:
$$a_k=\frac{f^{(k)}(a)}{k!}$$
con $0 \leq k \leq n$.

Así definimos:
$$T_{n,a}(x)= a_0+a_1(x-a)+ \ldots + a_n(x-a)^{n}$$
al polinomio de Taylor de grado $n$ de la función $f$ en $a$.
Por lo que:
$$T_{n,a}^{(k)}(a)=f^{(k)}(a)\quad , 0\leq k \leq n.$$

Definición de polinomio de Taylor

Definición (Polinomio de Taylor): Sea $f: (x_0,y_0) \rightarrow \r$, $a \in (x_0,y_0)$ con $f$ n-veces derivable en $a$. El polinomio de Taylor para $f$ con centro en $a$ de grado $n$ se define como:
$$T_{n,a}(x)=\sum_{j=0}^{n} \frac{f^{(j)}(a)}{j!}(x-a)^{j}$$
donde $f^{(0)}(a)=f(a)$.

¿Es una buena aproximación?

Ya que hemos definido al polinomio de Taylor para una función $f$, queremos saber si éste es una buena aproximación. Para ello veamos la demostración del siguiente teorema:

Teorema: Sea $f: (x_0,y_0) \rightarrow \r$, $a \in (x_0,y_0)$ tal que $f$ es de clase $C^{(n)}$ en $a \Rightarrow$ existe el polinomio de Taylor $T_{n,a}$ con:
$$a_k=\frac{f^{k}(a)}{k!} \quad , 0 \leq k \leq n$$
que cumple con que:
$$\lim_{x \to a} \frac{f(x)-T_{n,a}(x)}{(x-a)^{n}}=0$$

Demostración: Iniciemos sustituyendo por definición a $T_{n,a}(x)$
\begin{align*}
\frac{f(x)-T_{n,a}(x)}{(x-a)^{n}} &= \frac{f(x)- \sum_{j=0}^{n} \frac{f^{(j)}(a)}{j!}(x-a)^{j}}{(x-a)^{n}}\\
&= \frac{f(x)- \sum_{j=0}^{n-1} \frac{f^{(j)}(a)}{j!}(x-a)^{j}}{(x-a)^{n}} – \frac{\frac{f^{(n)}(a)}{n!}(x-a)^{n}}{(x-a)^{n}}\\
&= \frac{f(x)- \sum_{j=0}^{n-1} \frac{f^{(j)}(a)}{j!}(x-a)^{j}}{(x-a)^{n}} – \frac{f^{(n)}(a)}{n!}
\end{align*}

Para facilitar un poco la redacción consideremos a:
\begin{align*}
S(x)&=\sum_{j=0}^{n-1} \frac{f^{(j)}(a)}{j!}(x-a)^{j}\\
h(x)&= (x-a)^{n}
\end{align*}

Por lo que tenemos:
$$\frac{f(x)-S(x)}{h(x)}- \frac{f^{(n)}(a)}{n!} .$$

Probemos que el límite cuando $x$ tiende a $a$ es cero:
$$\lim_{x \to a} \frac{f(x)-S(x)}{h(x)}- \frac{f^{(n)}(a)}{n!} =0.$$

Que es equivalente a probar que:
$$\lim_{x \to a} \frac{f(x)-S(x)}{h(x)}=\frac{f^{(n)}(a)}{n!}.$$
Observemos que para $h$ se tiene en sus derivadas los siguiente:
\begin{align*}
h^{(0)}(x)&= (x-a)^{n} = \frac{n! (x-a)^{n-0}}{(n-0)!}\\
h^{(1)}(x)&= n (x-a)^{n-1} = \frac{n! (x-a)^{n-1}}{(n-1)!}\\
h^{(2)}(x)&= n (n-1)(x-a)^{n-2} = \frac{n! (x-a)^{n-2}}{(n-2)!}\\
\end{align*}
$$\vdots$$
$$h^{(k)}(x)=\frac{n! (x-a)^{n-k}}{(n-k)!}$$

Y para $S(x)$ vemos que sus derivadas en $a$ son:
\begin{align*}
S(x)&=a_0+a_1 (x-a)+a_2(x-a)^{2}+ \ldots + a_{n-1}(x-a)^{n-1}\\
&\Rightarrow S(a)=a_0\\
S^{(1)}(x)&= a_1+2 a_2 (x-a)+ \ldots +(n-1)a_{n-1}(x-a)^{n-2}\\
&\Rightarrow S^{(1)}(a)=a_1\\
S^{(2)}(x)&= 2a_2+ \ldots + (n-1)(n-2)a_{n-1} (x-a)^{n-3}\\
&\Rightarrow S^{(2)}(a)=2 a_3
\end{align*}
$$\vdots$$

Reescribiendo los $a_i$ obtenemos:
\begin{align*}
S^{(0)}(a)&= \frac{f^{(0)}(a)}{0!}=f^{(0)}(a)\\
S^{(1)}(a)&= \frac{f^{(1)}(a)}{1!}=f^{(1)}(a)\\
S^{(2)}(a)&= \frac{f^{(2)}(a)}{2!}(2)=f^{(2)}(a)\\
\end{align*}

$$\vdots$$

\begin{align*}
S^{(k)}(a)&= \frac{f^{(k)}(a)}{k!}(k!)=f^{(k)}(a)
\end{align*}

De este modo al considerar los límites:
\begin{align*}
\lim_{x \to a}(f(x)-S(x)) &= f(a)- S(a)=0\\
\lim_{x \to a}(f^{(1)}(x)-S^{(1)}(x)) &= f^{(1)}(a)- S^{(1)}(a)=0\\
\end{align*}
$$\vdots$$
\begin{align*}
\lim_{x \to a}(f^{(n-2)}(x)-S^{(n-2)}(x)) &=0\\
\end{align*}

Y los límites para $h$:
\begin{align*}
\lim_{x \to a}h(x)&= g(a)= (a-a)^{n}=0\\
\lim_{x \to a} h^{(1)}(x)&=g^{(1)}(a)= \frac{n! (a-a)^{n-1}}{(n-1)!}=0\\
\end{align*}
$$\vdots$$
\begin{align*}
\lim_{x \to a} h^{(n-2)}(x)&=g^{( n-2 )}(a)= 0\\
\end{align*}
Del análisis anterior notamos que podemos aplicar la Regla de L’Hôpital que nos decía que teniendo que: $$\lim_{x \to a^+} f(x) = 0 = \lim_{x \to a^+} g(x).$$

Si $\lim\limits_{x \to a^+} \frac{f'(x)}{g'(x)} = L \in \RR$, entonces $\lim\limits_{x \to a^+} \frac{f(x)}{g(x)} = L$.

Así al hacerlo $n-1$ veces en el siguiente límite se da la igualdad:
\begin{align*}
\lim_{x \to a}\frac{f(x)-S(x)}{(x-a)^{n}}&=\lim_{x \to a}\frac{f^{(n-1)}(x)-S^{(n-1)}(x)}{\frac{n!(x-a)^{n-n+1}}{(n-n+1)!}}\\
&=\lim_{x \to a}\frac{f^{(n-1)}(x)-S^{(n-1)}(x)}{\frac{n!(x-a)}{(1)!}}\\
&=\lim_{x \to a}\frac{f^{(n-1)}(x)-S^{(n-1)}(x)}{n! (x-a)}\\
\end{align*}

Recordemos que $S(x)$ es un polinomio de grado $n-1$ por lo que al haberlo derivado $n-1$ veces lo que obtenemos para $S^{(n-1)}(x)$ es una constante que resulta ser:
$$ S^{(n-1)}(x) = f^{(n-1)}(a).$$

Sustituyendo en el límite:
\begin{align*}
\lim_ {x \to a}\frac{f^{(n-1)}(x)-S^{(n-1)}(x)}{n! (x-a)} &= \lim_{x \to a}\frac{ f^{(n-1)}(x)- f^{(n-1)}(a)}{n! (x-a) }\\
&= \frac{1}{n!}\left(\lim_{x \to a}\frac{ f^{(n-1)}(x)- f^{(n-1)}(a)}{x-a} \right )
\end{align*}

De este modo el límite resultante es por definición la n-ésima derivada de $f$ en $a$, es decir:
$$ \lim_{x \to a}\frac{ f^{(n-1)}(x)- f^{(n-1)}(a)}{x-a} = f^{(n)}(a).$$

Consecuentemente:
$$\lim_{x \to a}\frac{f(x)-S(x)}{(x-a)^{n}}=\frac{ f^{(n)}(a)}{n!}.$$

$\square$

Con la demostración terminada podemos afirmar que los polinomios de Taylor son una buena aproximación, ahora veamos algunos ejemplos.

Ejemplo 1

Comencemos por obtener el polinomio de Taylor para la función exponencial en $a=0$:
$$f(x)=e^{x}.$$
Veamos que todas las derivadas son de la forma:
$$f^{(k)}(x)=e^{x}.$$
Por lo que la k-ésima derivada valuada en $a=0$:
$$f^{(k)}(a)=e^{0}=1.$$
Sustituyendo en la definición de polinomio de Taylor tenemos:
$$T_{n,a}(x)=\sum_{j=0}^{n} \frac{1}{j!}x^{j}$$
Comencemos por ver cuáles serían los polinomios de Taylor de grado $0$,$1$ y $2$:
\begin{align*}
T_{0,0}(x)&=\frac{1}{0!}\\
T_{1,0}(x)&= \frac{1}{0!} + \frac{1}{1!}(x-0)\\
T_{2,0}(x)&= \frac{1}{0!} + \frac{1}{1!}(x-0) + \frac{1}{2!}(x-0)^{2}\\
\end{align*}

Al graficar dichos polinomios notamos que entre mayor es el grado del polinomio, mejor es la aproximación a la función:

Ejemplo 2

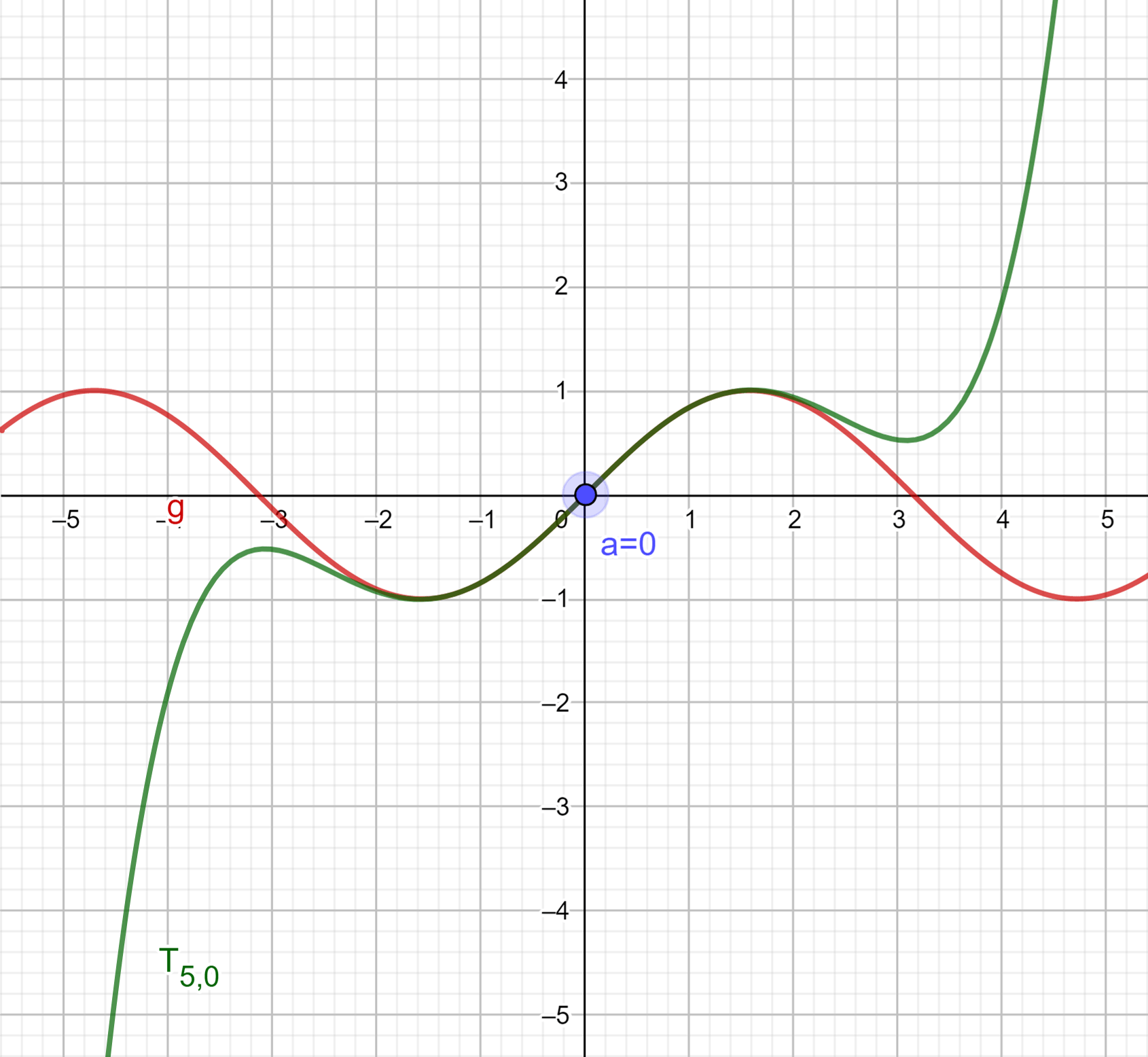
Ahora obtendremos el polinomio de Taylor de grado $5$ con centro en $a=0$ para:
$$g(x)=\sin(x).$$

Por lo que tenemos, calculamos las primeras cinco derivadas de $g$ y las evaluamos en cero:
\begin{align*}
g(x)&=\sin(0)=0\\
g^{(1)}(x)&=\cos(0)=1\\
g^{(2)}(x)&=-\sin(0)=0\\
g^{(3)}(x)&=-\cos(0)= -1\\
g^{(4)}(x)&=\sin(0)=0\\
g^{(5)}(x)&=\cos(0)=1\\
\end{align*}

Aplicando la definición de Taylor tenemos que su polinomio sería:
\begin{align*}
T_{5,0}&=\frac{0}{0!}(x-0)^{0}+\frac{1}{1!}(x-0)^{1}+\frac{0}{2!}(x-0)^{2}+\frac{(-1)}{3!}(x-0)^{3}+\frac{0}{4!}(x-0)^{4}+\frac{1}{5!}(x-0)^{5}\\
&=x-\frac{1}{3!}x^{3}+\frac{1}{5!}x^{5}
\end{align*}

Al graficar este polinomio $T_{5,0}=x-\frac{1}{3!}x^{3}+\frac{1}{5!}x^{5}$ vemos lo siguiente:

Ya que hemos revisado algunos ejemplos, en la siguiente sección te dejamos una lista de funciones de las que se te pide encontrar sus respectivos polinomios de Taylor siguiendo un procedimiento análogo.

Más adelante

Ahora que vimos la definición formal de los polinomios de Taylor, que resultan ser una buena aproximación para cualquier función $f$ con las características ya especificadas y algunos ejemplos, en la siguiente entrada veremos un resultado relacionado con su residuo.

Tarea moral

Obtener el polinomio de Taylor para las siguientes funciones:

  • $f(x)= \tan(x)$ de grado $3$ con $a=0$.
  • $g(x)= \sin(x)$ de grado $4$ con $a=\frac{\pi}{6}$.
  • $h(x)= e^{e^{x}}$ de grado $3$ con $a=0$.
  • $k(x)= \log(x+1)$ de grado $4$ con $a=0$.
  • $j(x)= \cos(x)$ de grado $m$ con $a=\frac{\pi}{2}$.

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»