Introducción

En esta entrada veremos cómo resolver, en $\mathbb{C}$, la ecuación $w^n=z$, en donde $z$ es un complejo y $n$ es un entero positivo. Puedes pensar esto como que aprenderemos a obtener raíces en los complejos, pero sólo para $n$ entero. Más adelante hablaremos de la función exponencial compleja que nos permitirá elevar a otro tipo de exponentes.

Nuestra herramienta principal será la fórmula de De Moivre, que ya demostramos en una entrada anterior. Encontrar raíces $n$-ésimas es una herramienta más en nuestra caja para trabajar con números complejos, que hasta el momento ya incluye resolver ecuaciones cuadráticas complejas y sistemas de ecuaciones lineales complejos.

Introducción a raíces en los complejos

Pensemos en un ejemplo sencillo. ¿Cuáles son los complejos $w$ tales que $w^4=1$? En $\mathbb{R}$ tenemos dos de ellos: $1$ y $-1$. Como $$(-i)^4=i^4=(-1)^2=1,$$ en $\mathbb{C}$ tenemos otras dos soluciones: $i$ y $-i$. Así que tenemos $4$ soluciones en $\mathbb{C}$: $1$, $-1$, $i$ y $-i$.

Para mostrar que son las únicas en este sencillo caso, podemos hacer lo siguiente. Expresamos $1$ en forma polar $1=\text{cis}(0)$ y también, en forma polar, una solución $w=s\text{cis}(\alpha)$, con $\theta$ en $[0,2\pi)$. Por el teorema de De Moivre, tenemos que $$1=w^4=s^4\text{cis}(4\alpha).$$

Así, la norma $s$ de $w$ debe satisfacer $s^4=1$, y además $\text{cis}(4\alpha)$ debe ser $1$, por lo que $4\alpha$ debe ser un múltiplo entero de $2\pi$. La norma es un real positivo, así que la única solución para $s$ es $1$. Ahora, ¿cuántos argumentos $\alpha$ en $[0,2\pi)$ hacen que $4\alpha$ sea un múltiplo entero de $2\pi$?

Para determinar esto, notemos que $4\alpha$ está en $[0,8\pi)$, y ahí hay exactamente cuatro múltiplos enteros de $2\pi$, que son $$0,2\pi, 4\pi, 6\pi.$$ Esto es justo lo que limita las soluciones a que sean a lo más $4$.

Podemos continuar para verificar que en efecto son las soluciones que ya encontramos. Las soluciones para $\alpha$ en cada caso son $$0,\frac{\pi}{2},\pi,\frac{3\pi}{2}.$$ Concluimos entonces que las soluciones complejas de $w^4=1$ son, en forma polar,
\begin{align*}
w_1&=\text{cis}(0)\\
w_2&=\text{cis}\left(\frac{\pi}{2}\right)\\
w_3&=\text{cis}\left(\pi\right)\\
w_4&=\text{cis}\left(\frac{3\pi}{2}\right),
\end{align*}

que son exactamente $1,i,-1,-i$.

$\square$

El teorema de raíces en los complejos

La discusión anterior funciona en general para cualquier entero positivo $n$ y para cualquier complejo $\mathbb{C}$. Siempre tenemos exactamente $n$ soluciones y sabemos cómo se ven en forma polar.

Teorema. Sea $z=r\text{cis}(\theta)$ un número complejo, distinto de cero, dado en forma polar y $n$ un entero positivo. Existen exactamente $n$ elementos distintos de $\mathbb{C}$ tales que $w^n = z$. Están dados en forma polar por $$w_j=r^{1/n} \text{cis}\left(\frac{\theta}{n} + j\frac{2\pi}{n}\right)$$ para $j=0,1,2\ldots,n-1$.

Demostración. Tomemos una solución $w$ y la escribimos en forma polar $w=s\text{cis}(\alpha)$, con $\alpha$ en $[0,2\pi)$. Usando que $w$ es solución y la fórmula de De Moivre, obtenemos que $$r\text{cis}(\theta)=s^n\text{cis}(n\alpha).$$ Como $s$ tiene que ser real positivo, obtenemos que $s=r^{1/n}$ (aquí estamos usando la raíz $n$-ésima en los reales).

El ángulo $n\alpha$ está en el intervalo $[0,2n\pi)$, y debe diferir en un múltiplo entero de $2\pi$ del ángulo $\theta$. Como $\theta$ está en $[0,2\pi)$, las únicas posibilidades para $n\alpha$ pueden ser los $n$ valores $$\theta, \theta+2\pi,\ldots, \theta+2(n-1)\pi,$$ de donde las soluciones para $\alpha$ son $$\frac{\theta}{n},\frac{\theta}{n}+\frac{2\pi}{n}, \ldots, \frac{\theta}{n} + (n-1)\frac{2\pi}{n},$$ respectivamente. Como son ángulos distintos en $[0,2\pi)$, obtenemos las posibles soluciones distintas $$r^{1/n} \text{cis}\left(\frac{\theta}{n} + j\frac{2\pi}{n}\right)\quad \text{para $j=0,\ldots,n-1$}.$$

Verificar que en efecto son soluciones es sencillo, ya sea revirtiendo los pasos que hicimos, o usando directamente la fórmula de De Moivre. Esta verificación queda como tarea moral.

$\square$

Observa que el teorema dice que para obtener una raíz podemos empezar del complejo de norma $r^{1/n}$ y argumento $\frac{\theta}{n}$, y de ahí obtener el resto de las raíces en los complejos «rotando repetidamente $\frac{2\pi}{n}$ en el plano complejo». Esto muestra que las raíces forman los vértices de un $n$-ágono regular.

Nos costó un poco de trabajo mostrar que teníamos a lo más $n$ soluciones. En realidad, cualquier ecuación polinomial de grado $n$, es decir, de la forma $$a_nx^n+a_{n-1}x^{n-1}+\ldots+a_1x+a_0=0$$ tiene a lo más $n$ soluciones. Esto lo veremos con toda generalidad en la última unidad, cuando hablemos de polinomios.

Ejemplos de obtener raíces en los complejos

Ejemplo. Encontremos todas las raíces séptimas del complejo $128\text{cis}\left(\frac{14\pi}{13}\right)$. Para empezar, notemos que $128^{1/7}=2$, de modo que todas las raíces tienen norma $2$.

Una de las raíces tiene argumento $\frac{14\pi}{7\cdot 13}=\frac{2\pi}{13}$ y el argumento del resto difiere en múltiplos enteros de $\frac{2\pi}{7}$. De esta forma, las raíces son

\begin{align*}
w_1&=2\text{cis}\left(\frac{2\pi}{13}\right)\\
w_2&=2\text{cis}\left(\frac{2\pi}{13}+\frac{2\pi}{7}\right)=2\text{cis}\left(\frac{40\pi}{91}\right)\\
w_3&=2\text{cis}\left(\frac{2\pi}{13}+\frac{4\pi}{7}\right)=2\text{cis}\left(\frac{66\pi}{91}\right)\\
w_4&=2\text{cis}\left(\frac{2\pi}{13}+\frac{6\pi}{7}\right)=2\text{cis}\left(\frac{92\pi}{91}\right)\\
w_5&=2\text{cis}\left(\frac{2\pi}{13}+\frac{8\pi}{7}\right)=2\text{cis}\left(\frac{118\pi}{91}\right)\\
w_6&=2\text{cis}\left(\frac{2\pi}{13}+\frac{10\pi}{7}\right)=2\text{cis}\left(\frac{144\pi}{91}\right)\\
w_7&=2\text{cis}\left(\frac{2\pi}{13}+\frac{12\pi}{7}\right)=2\text{cis}\left(\frac{170\pi}{91}\right).
\end{align*}

$\square$

Problema. Sabemos que $(2-3i)^4=-119+120i$. Encuentra las otras raíces cuartas de $-119+120i$.

Solución. Podríamos pasar $-119+120i$ a forma polar y usar el método anterior. Esto funciona y dará una solución. Pero veamos una solución alternativa más corta, que nos ayuda a entender mejor el teorema de raíces en los complejos.

De acuerdo con lo que probamos, las raíces varían únicamente en argumento, al que se le va sumando $\frac{\pi}{2}$. Es decir, si tenemos una raíz en el plano complejo, las demás se obtienen de ir rotando $\frac{\pi}{2}$ (recuerda que esto es $90^\circ$) desde el origen. Al ir rotando el punto $(2,-3)$ en el plano complejo en este ángulo, obtenemos los puntos $(-3,-2)$, $(-2,3)$ y $(3,2)$, de modo que las otras tres raíces son $-3-2i$, $-2+3i$ y $3+2i$.

Otra forma más de pensarlo es la siguiente. Si ya tenemos una raíz cuarta $w$ de un complejo $z$, entonces todas las raíces se obtienen multplicando por $1,i,-1, -i$. En efecto, por ejemplo, $$(iw)^4=i^4w^4=w^4=1.$$ Así, para el problema que nos interesa, las soluciones son

\begin{align*}w_1&=2-3i\\w_2&=i(2-3i)=3+2i\\w_3&=-(2-3i)=-2+3i\\w_4&=-i(2-3i)=-3-2i,\end{align*}
lo cual coincide con lo que habíamos encontrado antes.

$\square$

Raíces $n$-ésimas de la unidad

Un caso particular importante de la teoría desarrollada en la sección anterior es cuando $z$ es $1$. Sea $n$ un entero positivo y $w$ un complejo tal que $w^n=1$. A $w$ se le conoce como una raíz $n$-ésima de la unidad.

Teorema (de las raíces $n$-ésimas de la unidad). Sea $n$ un entero positivo. Existen exactamente $n$ raíces $n$-ésimas de la unidad distintas. Si $\omega$ es la que tiene el menor argumento positivo, entonces dichas raíces son $$1,\omega, \omega^2,\ldots, \omega^{n-1}.$$

La demostración se sigue fácilmente del teorema de raíces $n$-ésimas y queda como tarea moral. Cualquier raíz $n$-ésima $\omega$ tal que sus primeras potencias generen todas las raíces $n$-ésimas de la unidad se le conoce como una raíz primitiva.

Las raíces $n$-ésimas de la unidad tienen una interpretación geométrica bonita. Forman los vértices del $n$-ágono regular con $n$ vértices, sobre la circunferencia unitaria, donde uno de los vértices es $1$.

Ejemplo. Obtengamos las raíces quintas de la unidad. Primero, obtengamos la de menor argumento positivo, que por el teorema de raíces en los complejos, es $$\omega = \text{cis}\left(\frac{2\pi}{5}\right).$$ El resto de las raíces son entonces $\omega^2$, $\omega^3$, $\omega^4$ y $1$. Las podemos encontrar en el plano complejo como vértices del siguiente pentágono regular:

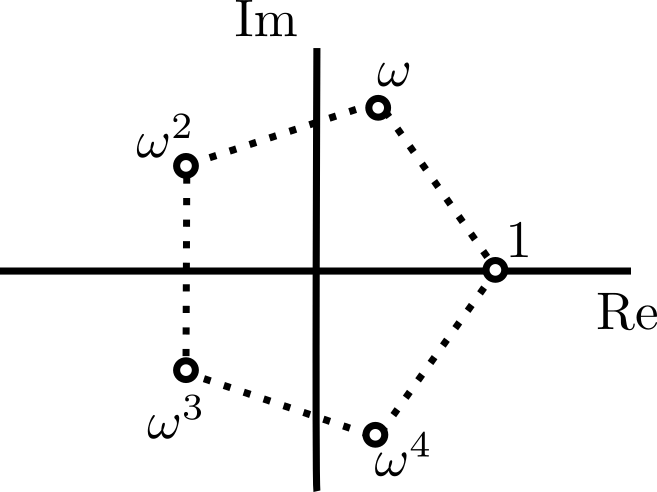
Cualquiera de $\omega$, $\omega^2$, $\omega^3$ y $\omega^4$ son raíces primitivas, pero $1$ no es raíz primitiva pues sus potentcias sólo son él mismo.

$\square$

Las raíces $n$-ésimas de la unidad se utilizan en muchos contextos. Aunque se puede trabajar con ellas de forma explícita, muchas veces se utilizan sólo las propiedades algebraicas que cumplen. A continuación enunciamos algunas.

Teorema. Sea $\omega$ una raíz primitva $n$-ésima de la unidad. Las raíces $n$-ésimas de la unidad $$\omega_i = \omega^i $$ para $i=0,\ldots,n-1$ satisfacen las siguientes propiedades:

• Para $n>1$, se tiene que $\omega_0+\ldots+\omega_{n-1}=0$.
• Para $k=0,1,\ldots,n-1$, se tiene que $$(\omega_k)^{-1}=\overline{\omega_k}=\omega_{n-k}.$$
• Se tiene que $\omega_0\cdot\ldots\cdot \omega_{n-1} = (-1)^{n+1}$.

Demostración. Empezamos con el primer inciso. Si $n>1$, tenemos que $1$ no es raíz primitiva, así que para el primer inciso sabemos que $\omega\neq 1$. Usamos la fórmula para suma de términos en una progresión geométrica:
\begin{align*}
\omega_0+\omega_1&+\ldots+\omega_{n-1}\\
&= 1+\omega+\ldots+\omega^{n-1}\\
&=\frac{1-\omega^n}{1-\omega}\\
&=\frac{1-1}{1-\omega}\\
&=0.
\end{align*}

Para la segunda parte, notemos que $$\omega_k\omega_{n-k}=\omega^k\omega^{n-k}=\omega^n=1,$$ lo cual prueba una de las igualdades. La otra igualdad se sigue del hecho general que el inverso de un complejo de norma $1$ es su conjugado, cuya demostración queda como tarea moral.

La tercera parte se sigue de la propiedad anterior. Al multiplicar todas las raíces de la unidad, podemos emparejar a cada raíz con su conjugado para obtener producto $1$. Las únicas excepciones es cuando emparejamos a un complejo consigo mismo, es decir, para cuando $\omega_k=\overline{\omega_k}$, lo cual sucede sólo cuando $\omega_k$ es real. Las únicas posibilidades son $1$ ó $-1$. El $1$ no tiene problema pues colabora con un factor $1$. Si $n$ es impar, $-1$ no es raíz $n$-ésima, así que no contribuye al producto. Si $n$ es par sí. Esto muestra lo que queremos pues $(-1)^{n+1}$ es $1$ si $n$ es impar y $-1$ si es par.

$\square$

Para un entero positivo $n$, llamemos $(U_n,\cdot)$ al conjunto de raíces $n$-ésimas de la unidad equipadas con el producto complejo.

Teorema. Para cada entero positivo $n$, se tiene que $(U_n,\cdot)$ es un grupo y es isomorfo a $(\mathbb{Z}_n,+)$.

Demostración. El producto de cualesquiera dos raíces $n$-ésimas es también una raíz $n$-ésima. Por el teorema anterior, los inversos multiplicativos de las raíces $n$-ésimas también son raíces $n$-ésimas. Esto basta para mostrar que se forma un grupo.

Para la segunda parte, notamos que ambos grupos son el grupo cíclico de $n$ elementos. Una correspondencia entre ellos está dada por mandar $[1]_n$ a cualquier raíz primitiva.

$\square$

Más adelante…

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

1. Encuentra las raíces cúbicas de $8-8i$ y dibújalas en el plano complejo.
2. Verifica que las soluciones obtenidas en el teorema de raíces $n$-ésimas en efecto son soluciones.
3. Muestra el teorema de las raíces $n$-ésimas de la unidad.
4. Prueba que si $z$ es un complejo de norma $1$, entonces su inverso es su conjugado.
5. Sea $\omega$ una raíz $n$-ésima primitiva de la unidad. Muestra que $w^k$ es una raíz primitiva si y sólo si $n$ y $k$ son primos relativos, es decir, $\MCD{n,k}=1$. Sugerencia: Usa lo que sabemos de soluciones a ecuaciones diofantinas lineales.
6. Encuentra de manera explícita la parte real y la parte imaginaria de todas las raíces quintas de la unidad.
   Sugerencia: La ecuación $w^5-1=0$ se puede factorizar como $$(w-1)(w^4+w^3+w^2+w+1)$$ y $w^4+w^3+w^2+w+1$ se puede factorizar como $$\left(w^2+\frac{1+\sqrt{5}}{2}w+1\right)\left(w^2+\frac{1-\sqrt{5}}{2}w+1\right).$$ Usa lo que sabemos de resolver ecuaciones cuadráticas cojmplejas.

Entradas relacionadas

• Ir a: Álgebra Superior II
• Entrada anterior del curso: Multiplicación en forma polar y fórmula de De Moivre
• Entrada siguiente del curso: Problemas de fórmula de De Moivre y raíces n-ésimas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»