Introducción

A continuación definiremos algunas de las operaciones que hay entre conjuntos como lo son la unión, intersección y diferencia. Retomaremos algunos axiomas como el de unión y el esquema de comprensión, para ver que estas operaciones definen nuevos conjuntos.

Unión

Recordemos la definición de la unión de dos conjuntos.

Definición. Si $A$ y $B$ son conjuntos, entonces definimos la unión de $A$ y $B$ como:

$A\cup B=\bigcup\set{A,B}$

o bien,

$A\cup B= \set{x: x\in A\ o\ x\in B}$.

Ejemplos.

1. Consideremos los conjuntos $A= \set{\emptyset}$ y $B= \set{\emptyset, \set{\emptyset}}$. Luego, $A\cup B=\bigcup\set{A,B} = \bigcup\set{\emptyset, \set{\emptyset, \set{\emptyset}}}=\set{\emptyset,\set{\emptyset}}=B$.
2. Ahora, consideremos $A=\set{\set{\emptyset}}$ y $B=\set{\set{\set{\emptyset}}}$. Tendremos que $A\cup B=\set{\set{\emptyset}}\cup \set{\set{\set{\emptyset}}}=\set{\set{\emptyset},\set{\set{\emptyset}}}$.

$\square$

Propiedades de la unión

Proposición. Para cualquier conjunto $A$ se tiene que $A\subseteq A\cup B$. Además, $A\cup B= B\cup A$.

Demostración.

Primero veamos que $A\subseteq A\cup B$. Supongamos que $x\in A$, entonces existe $A\in \set{A, B}$ tal que $x\in A$. Esto es, por definición de unión que $x\in \bigcup \set{A,B}=A\cup B$.

Para ver que $A\cup B=B\cup A$, notemos que $A\cup B=\bigcup\set{A,B}$ y $B\cup A=\bigcup \set{B, A}$. Sabemos que $\set{A, B}=\set{B, A}$ por axioma de extensión. Así, $A\cup B=B\cup A$.

$\square$

Intersección

Definición. Sean $A$ y $B$ conjuntos. La intersección de dos conjuntos estará definida como sigue:

$A\cap B=\set{x: x\in A\land x\in B}$.

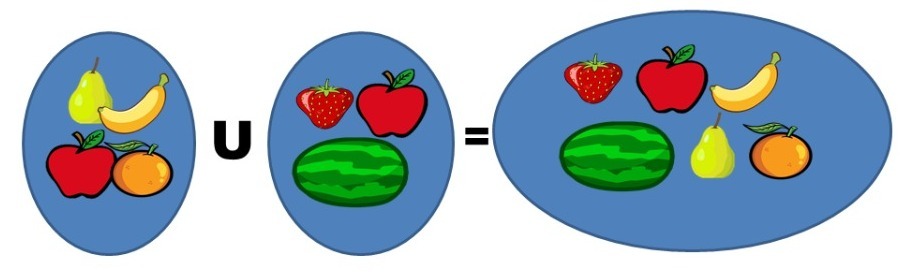
La intersección de dos conjuntos nos permite obtener un conjunto cuyos elementos son aquellos que se encuentran en ambos conjuntos. En la imagen que proporcionamos arriba podemos ver que la intersección nos deja solamente a la manzana y la pera, pues están en ambos conjuntos y descarta al plátano y la naranja pues solo viven en el primer conjunto. Lo mismo hace con la fresa y la sandía que solo viven en el segundo conjunto.

Proposición. $A\cap B$ es un conjunto.

Demostración. Sean $A$ y $B$ conjuntos.

Definamos la propiedad «$P(x): x\in B$». Por el esquema de comprensión se tiene que

$\set{x\in A:x\in B}$

es un conjunto.

Luego, $\set{x\in A:x\in B}=A\cap B$. En efecto, $z\in A\cap B$ si y sólo si $z\in A$ y $z\in B$ si y sólo si $z\in \set{x\in A:x\in B}$.

Por lo tanto, $A\cap B$ es conjunto.

$\square$

Ejemplos.

1. Consideremos $A=\set{\emptyset}$ y $B=\set{\set{\emptyset}}$, tenemos que $A\cap B=\emptyset$ esto último debido a que no existe ningún elemento $x$ tal que $x\in \set{\emptyset}$ y $x\in\set{\set{\emptyset}}$ al mismo tiempo. De ocurrir, tendriamos que $x=\emptyset$ y $x=\set{\emptyset}$ y por lo tanto, $\emptyset=\set{\emptyset}$ lo cual sabemos que no ocurre. Por lo tanto, $A\cap B=\emptyset$.
2. Sean $A=\set{\emptyset,\set{\emptyset}}$ y $B=\set{\emptyset}$ conjuntos. Notemos que en este ejemplo el único elemento que está tanto en el conjunto $A$ como en el conjunto $B$ es $x=\emptyset$. De este modo, $A\cap B=\set{\emptyset}$.

$\square$

También podemos definir intersecciones arbitrarias, no sólo de dos conjuntos.

Definición. Sea $A$ un conjunto no vacío, definimos a la intersección de $A$ como la colección:

$\set{x: \forall y\in A(x\in y)}$.

Ejemplo.

Sea $A=\set{\set{\emptyset}, \set{\set{\emptyset}}, \set{\emptyset, \set{\emptyset}}}$, tenemos que la intersección de $A$ es $\emptyset$. En efecto, esto pasa ya que no existe ningún elemento $x$ que pertenezca a todos los elementos de $A$.

$\square$

Ejemplo.

Sea $X=\set{A,B}$ con $A$ y $B$ conjuntos. Resulta que $\bigcap X= \bigcap \set{A, B}= A\cap B$. En efecto, $x\in \bigcap X$ si y sólo si para todo $y\in X$, $x\in y$ si y sólo si $x\in A$ y $x\in B$.

$\square$

El hecho de que la unión arbitraria es conjunto es resultado del axioma de la unión. No hay un axioma de la intersección, por lo que demostraremos que la intersección de un conjunto $A$ es un conjunto, siempre que $A$ no sea vacío.

Proposición. Para todo $A\not=\emptyset$, la intersección de $A$ es un conjunto.¹

Demostración:

Sea $A$ conjunto no vacío, entonces $A$ tiene al menos un elemento. Sea $z\in A$, tenemos que $\set{x\in z: \forall y\in A(x\in y)}$ es conjunto por esquema de comprensión.

Resulta que $a\in \set{x\in z: \forall y\in A(x\in y)}$ si y sólo si $a\in y$ para todo $y\in A$. En efecto, si $a\in \set{x\in z: \forall y\in A(x\in y)}$, entonces $a\in z$ y $\forall y\in A$, $a\in y$. Entonces $a\in y$ para todo $y\in A$.

Ahora, si $a\in y$ para todo $y\in A$, en particular $a\in z$ pues $z\in A$. Por tanto, $a\in \set{x\in z: \forall y\in A(x\in y)}$.

$\square$

Si observamos, para realizar la demostración anterior usamos el hecho de que $A\not=\emptyset$, por lo que podríamos preguntarnos qué pasa si $A$ es vacío. Veremos esto con detalle en la siguiente entrada.

Ahora que hemos probado que la intersección de $A$ es un conjunto cuando $A$ es no vacío, le asignaremos una notación la cual estará dada por $\bigcap A$.

Propiedades de la intersección

Teorema. Para cualesquiera $A$, $B$ conjuntos, tenemos que:

1. $A\cap B\subseteq A$,
2. $A\cap A=A$,
3. $A\cap B=B\cap A$.

Demostración.

1. Sea $x\in A\cap B$. Veamos que $x\in A$.
   Como $x\in A\cap B$ tenemos por definición de intersección que $x\in A$ y $x\in B$. En particular, $x\in A$. Por lo tanto, $A\cap B\subseteq A$.
2. Tomemos $x\in A\cap A$. Veamos que $x\in A$.
   Que $x\in A\cap A$ es equivalente a decir que $x\in A$ y $x\in A$, lo cual pasa si y sólo si $x\in A$. Por lo tanto, $A\cap A=A$.
3. $A\cap B=B\cap A$ pues $x\in A\cap B$ arbitrario si y sólo si $x\in A$ y $x\in B$, si y sólo si $x\in B$ y $x\in A$, si y sólo si $x\in B\cap A$.

$\square$

Diferencia

Definición. Sean $A$ y $B$ conjuntos. La diferencia de $A$ con $B$ estará definida como sigue:

$A\setminus B=\set{x\in A: x\notin B}$.

Por esquema de comprensión $A\setminus B$ es conjunto.

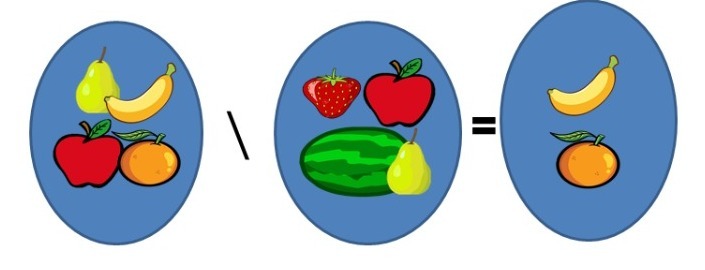
La diferencia entre dos conjuntos nos permite obtener un conjunto cuyos elementos se encuentra en el primero pero no el segundo conjunto. En la imagen anterior podemos ver que la diferencia nos deja solamente al plátano y la naranja, pues el plátano y la naranja se encuentran en el primer conjunto, pero no en el segundo. La manzana y la pera no forma parte del conjunto final pues vive en ambos conjuntos. La fresa no es elemento de la diferencia pues ni siquiera es elemento del primer conjunto.

Ejemplos.

1. Consideremos $A=\set{\emptyset}$ y $B=\set{\set{\emptyset}}$, tenemos que $A\setminus B=\set{\emptyset}$ pues el único elemento que cumple estar en $A$ y no pertenecer al conjunto $B$ es $\emptyset$.
2. Sea $A=\set{\emptyset, \set{\emptyset}}$ y $B=\set{\emptyset}$. Luego,
   $A\setminus B=\set{x\in A:x\notin B}=\set{x\in \set{\emptyset, \set{\emptyset}}: x\notin\set{\emptyset}}= \{\set{\emptyset}\}$.

Propiedades de la diferencia

Teorema. Para cualesquiera $A$, $B$ conjuntos, tenemos que:

1. $A\setminus \emptyset= A$,
2. $A\setminus A=\emptyset$,
3. $A\setminus B=A\setminus (A \cap B)$.

Demostración.

1. Sea $x\in A\setminus \emptyset$. Entonces $x\in A$ y $x\notin \emptyset$. En particular $x\in A$, por lo tanto $A\setminus \emptyset\subseteq A$.
   Luego, supongamos que $x\in A$. Como $x\notin \emptyset$ es verdadero para cualquier conjunto $x$, tenemos que $x\in A$ y $x\notin \emptyset$ es verdadero. Por lo tanto, $x\in A\setminus \emptyset$ y así $A\subseteq A\setminus \emptyset$.
   De lo anterior tenemos que $A=A\setminus \emptyset$.
2. Supongamos que $A\setminus A\not=\emptyset$, es decir, existe al menos un elemento $x\in A\setminus A$. Entonces $x\in A$ y $x\notin A$, lo cual no puede ocurrir. Dado que la contradicción provino de suponer que $A\setminus A\not=\emptyset$, concluimos que $A\setminus A=\emptyset$.
3. Veamos que $A\setminus B=A\setminus (A \cap B)$.
   $\subseteq$] Sea $x\in A\setminus B$, entonces $x\in A$ y $x\notin B$. Luego, como $x\notin B$ entonces $x\notin A$ o $x\notin B$ es verdadero. Lo que equivale a decir que $x\notin (A\cap B)$. Por lo tanto, $x\in A$ y $x\notin (A \cap B)$ y así, $A\setminus B\subseteq A\setminus(A\cap B)$.
   $\supseteq$] Sea $x\in A\setminus (A\cap B)$, entonces $x\in A$ y $x\notin (A\cap B)$. Lo que equivale a decir que $x\in A$ y ($x\notin A$ o $x\notin B$). Dado que $x\notin A$ no puede ocurrir pues $x\in A$, entonces $x\notin B$. Por lo tanto, $x\in A$ y $x\notin B$ y así, $A\setminus(A\cap B)\subseteq A\setminus B$.
   Por lo tanto, $A\setminus(A\cap B)= A\setminus B$.

$\square$

Proposición. $A\setminus B=\emptyset$ si y sólo si $A\subseteq B$.

Demostración.

Supongamos que $A\setminus B=\emptyset$ y supongamos que $A\nsubseteq B$ en busca de una contradicción. Como $A\nsubseteq B$, existe $x\in A$ tal que $x\notin B$, y por lo tanto, $x\in A\setminus B$, lo que contradice que $A\setminus B=\emptyset$.
Por lo tanto, $A\subseteq B$.

Ahora, si $A\subseteq B$, entonces para cualquier $x\in A$, $x\in B$, por lo que no es posible que $A\setminus B$ sea no vacío.

$\square$

Tarea moral

Los siguientes ejercicios te servirán para poner en práctica los conocimientos que has adquirido en este sección, en la siguiente lista podrás probar las siguientes propiedades de la unión, intersección y diferencia de conjuntos:

1. Prueba que $A\cap \emptyset=\emptyset$ para todo conjunto $A$.
2. Prueba que para cualesquiera $A$, $B$ y $C$ conjuntos:
   – $A\cup(B\cup C)=(A\cup B)\cup C$.
   – $A\cap (B\cap C)= (A\cap B)\cap C$.
3. Prueba que para cualesquiera $A$, $B$ y $C$ conjuntos:
   – $A\cup (B\cap C)= (A\cup B)\cap(A\cup C)$,
   – $A\cap (B\cup C)= (A\cap B)\cup(A\cap C)$.
4. Si $A\subseteq C$ y $B\subseteq D$ entonces $A\cap B\subseteq C\cap D$.
5. Demuestra que $A\setminus B=A$ si y sólo si $A\cap B=\emptyset$.
6. Demuestra a partir de los axiomas que en efecto si $A$ es un conjunto no vacío, entonces $\cap A$ es conjunto.

Más adelante…

En la siguiente entrada retomaremos la definición de intersección de conjuntos y mencionaremos el axioma de buena fundación. Además abordaremos el tema de la colección de todos los conjuntos apoyados de este último axioma. Finalmente, veremos que la intersección del conjunto vacío resulta ser la colección de todos los conjuntos.

Entradas relacionadas

• Entradas relacionadas: Álgebra Superior I: Intersecciones, uniones y complementos de conjuntos
• Álgebra Superior I: Leyes de De Morgan y diferencia simétrica de conjuntos
• Ir a Teoría de los Conjuntos I
• Entrada anterior: Teoría de los Conjuntos I: Axioma de conjunto potencia
• Siguiente entrada: Teoría de los Conjuntos I: El axioma de buena fundación

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE109323 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 3»

1. También puedes consultar la demostración de este resultado en: Amor, J. A., Teoría de Conjuntos para Estudiantes de Ciencias, México: Serv. Editoriales Fac. Ciencias, UNAM, 1997, p. 17. ↩︎