Introducción
Esta sección estará dedicada a un tipo de relaciones a las que llamaremos funciones. Este tema será de gran importancia pues utilizaremos funciones con mucha frecuencia a partir de ahora, es por ello que dedicaremos una serie de entradas para tratarlas. En esta primera parte abordaremos la definición de función, algunas de sus propiedades y ejemplos.
¿Qué es una función?
La motivación de la definición de función es la siguiente. Tomemos $A$ y $B$ conjuntos. Queremos poder asignar a cualquier elemento de $A$ uno y sólo un elemento de $B$, de manera que inequívocamente para cada $a\in A$ podamos hablar del elemento que se le asignó en $B$. Las relaciones ayudan a emparejar elementos de $A$ y $B$, pero podemos tener dos problemas 1) Que no todo elemento de $A$ esté en alguna pareja de la relación o 2) Que algún elemento de $A$ quede emparejado con más de un elemento de $B$. Por ello, la definición de función queda establecida de la siguiente manera.
Definición. Sean $A$ y $B$ conjuntos. Una función $f$ de $A$ en $B$ es una relación $f\subseteq A\times B$ que satisface:
- Para cualquier $x\in A$, existe $y\in B$ tal que $(x,y)\in f$.
- Para cualesquiera $a\in A$ y $b,c\in B$, si $(a,b)\in f$ y $(a,c)\in f$, entonces $b=c$.
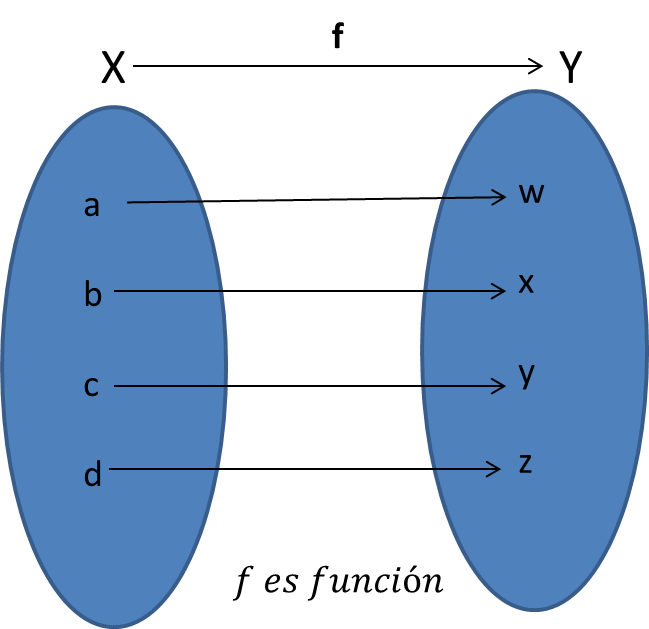
La definición anterior nos dice que dados dos conjuntos y una relación $R$ de $A$ en $B$, esta es una función si y sólo si cada elemento del $dom(R)$ esta relacionado con uno y sólo uno de $B$. Como se muestra en la siguiente imagen:
Para abordar la definición desde otra perspectiva revisaremos el siguiente ejemplo que nos muestra que no toda relación es función.
Ejemplo.
Sea $A=\set{1,2}$ y $B=\set{1,2,3}$. Sea $R$ una relación de $A$ en $B$ dada por $R=\set{(1,1), (1,2), (2,1)}$.
Resulta que $R$ no es función pues $(1,1)\in R$ y $(1,2)\in R$, sin embargo no es cierto que $1=2$.
$\square$
Ahora veamos el ejemplo de una relación que si es función.
Ejemplo.
Sea $A=\set{1,2,3}$ y $B=\set{1,2}$. Sea $f$ una relación de $A$ en $B$ dada por $f=\set{(1,1), (2,1), (3,1)}$.
En este ejemplo tenemos que $f$ es función pues cada elemento de $A$ está relacionado con uno y sólo uno de $B$, es decir, para cualesquiera $(a,b)\in f$ y $(a,c)\in f$ se cumple que $b=c$.
$\square$
Después de revisar estos ejemplos es importante mencionar que aunque no toda relación es función, siempre ocurrirá que una función es una relación, este último hecho se sigue de la definición de función.
Función vacía
Observa que si $X=\emptyset$ y $Y$ es un conjunto cualquiera, entonces el conjunto vacío es una función de $X$ en $Y$. En la sección de relaciones vimos que el conjunto vacío en efecto es una relación, nos resta ver que para cualesquiera $(a,b)\in f$ y $(a,c)\in f$ se cumple que $b=c$, sin embargo este enunciado se cumple por un argumento por vacuidad.
Por lo tanto, la relación vacía es función.
Función constante
Sean $X$, $Y$ conjuntos y $c\in Y$. Definimos la función $f_c$ de $X$ en $Y$ como $f_c=X\times \{c\}$. Nuestra función se verá de la siguiente forma:
Función identidad
Sea $X$ un conjunto, la relación identidad es función. Recordemos que la relación identidad $Id_X$ esta definida como sigue:
$Id_X=\set{(x,y)\in X\times Y: x=y}$
Dado que para cualesquiera $(x,y)\in Id_X$ y $(x,w)\in Id_X$ tenemos que $x=y$ y $x=w$ por definición de la relación $Id_X$, por lo tanto, $y=w$ y así concluimos que $Id_X$ es función.
Función característica
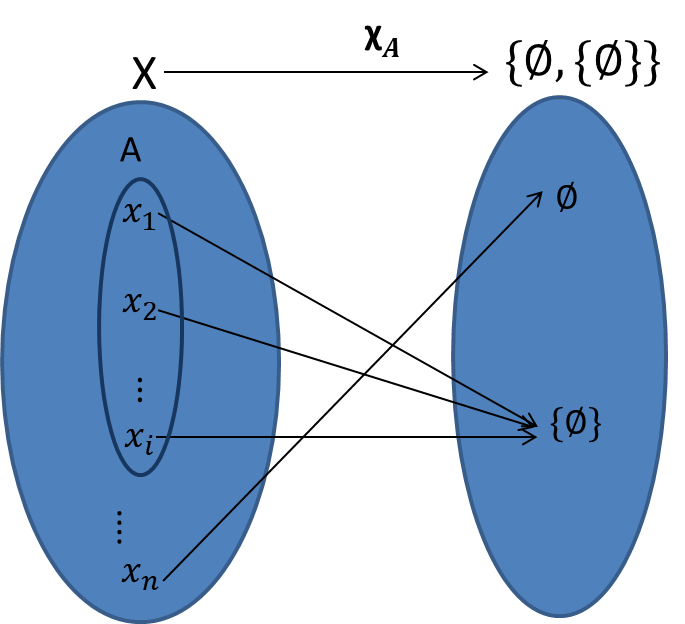
Sean $A$ y $X$ conjuntos tales que $A\subseteq X$, definimos a la función característica $\chi_A$ de $A$ en $\set{\emptyset, \set{\emptyset}}$ como $\chi_A=\{(x, \{\emptyset\}):x\in A \}\cup \{(x, \emptyset):x\in X\setminus A\}$.
Función inclusión
Sea $X$ un conjunto cualquiera, definimos a la función inclusión como el siguiente conjunto:
$\iota_A= \set{(x,x):x\in A}$.
Debido a que las funciones serán recurrentes en las entradas subsecuentes, es necesario adoptar alguna notación para estos conceptos. Dada una relación $f$ de $A$ en $B$ utilizaremos la notación $f:A\to B$ para indicar que $f$ es una función. Ahora bien, si $f:A\to B$ y $x\in A$ y $y\in B$, escribiremos $f(x)=y$ si $(x,y)\in f$.
Dominio e imagen
De manera similar que con las relaciones trataremos las definiciones de dominio, imagen e imagen inversa, sin embargo ahora lo haremos para funciones.
Definición. Sea $f$ una función de A en B, definimos el dominio de la $f$ como:
$dom(f)=\set{x\in A:\exists y\in B(f(x)=y)}$.
Ejemplo.
Sea $A=\set{1,2,3,4}$ y $B=\set{1,2,3,4}$. Sea $f:A\to B$ una función dada por el conjunto $f=\set{(1,1), (2,2), (3,3), (4,4)}$.
Tenemos que,
$dom(f)=\set{x\in \set{1,2,3,4}:\exists y\in \set{1,2,3,4}(f(x)=y)}=\set{1,2,3,4}$.
$\square$
Definición. Sea $f$ una función de A en B, definimos la imagen de la función $r$ como:
$im(f)=\set{y\in B:\exists x\in A(f(x)=y)}$.
Ejemplo.
Sea $A=\set{1,2,3,4}$ y $B=\set{1}$. Sea $f:A\to B$ una función dada por $f(x)=1$ para todo $x\in A$.
Tenemos que,
$im(f)=\set{y\in B: \exists x(f(x)=y)}=\set{1}$.
$\square$
Definición. Sea $f$ una función de $A$ en $B$ y sea $D\subseteq A$. Definimos la imagen de $D$ bajo la función $f$ como el conjunto:
$f[D]=\set{f(x)\in B: \exists x\in D(f(x)=y)}$.
Ejemplo.
Sea $A=\set{1,2,3,4}$ y $B=\set{2,4,6,8}$. Sea $f:A\to B$ una función dada por $f(x)=2x$ para todo $x\in A$. Sea $A’=\set{2,4}\subseteq A$.
Tenemos que,
$f[A’]=\set{f(x)\in B: \exists x\in A'(f(x)=y)}=\set{4,8}$.
$\square$
Definición. Sea $f$ una función de $A$ en $B$ y sea $B’\subseteq B$. Definimos la imagen inversa de $B’$ bajo la función $f$ como el conjunto:
$f^{-1}[B’]=\set{x\in A: \exists y\in B'(f(x)=y)}$.
Ejemplo.
Sea $A=\set{1,2,3,4}$ y $B=\set{2,4,6,8}$. Sea $f:A\to B$ una función dada por $f(x)=2x$ para todo $x\in A$. Sea $B’=\set{2,4}\subseteq B$.
Tenemos que,
$f^{-1}[B’]=\set{x\in A: \exists y\in B'(f(x)=y)}=\set{1,2}$.
$\square$
Tarea moral
Los siguientes ejercicios te ayudarán a reforzar los conceptos de función, dominio e imagen.
- Sea $f$ una función de $\set{1,2}$ en $\set{2,4,5}$ dada por $f=\set{(1,2), (2,4)}$. Describe al dominio y la imagen de $f$.
- Sean $A=\set{1,2,3,4,5,6,7,8,9}$ y $B=\set{1,2,3,4,5,6,7}$ conjuntos. Responde si las siguientes relaciones son o no funciones:
1. $f_1=\set{(1,1), (1,2), (2,1), (3,4)}$,
2. $f_2=\set{(1,1), (2,2), (3,3), (4,4) (5,5)}$,
3. $f_3=\set{(1,1), (2,1), (3,1), (4,1), (5,1)}$.
Más adelante…
La siguiente sección estará dedicada a hablar acerca de algunas de las propiedades que tiene la imagen de un conjunto bajo una función respecto a la unión, la intersección y la diferencia. Además hablaremos acerca de la composición de funciones, en esta parte retomaremos el concepto de composición de relaciones.
Entradas relacionadas
- Entrada relacionada: Álgebra Superior I: Introducción a funciones
- Ir a Teoría de los Conjuntos I
- Entrada anterior: Teoría de los Conjuntos I: Composición de relaciones
- Siguiente entrada: Teoría de los conjuntos I: Funciones (parte II)