Introducción
En la entrada puntos nobles del triangulo, vimos que las medianas de un triangulo concurren en un punto, al que llamamos centroide, y que este punto tiene la propiedad de trisecar a las medianas. En esta entrada estudiaremos algunas propiedades más de las medinas y el centroide.
Medianas como los lados de un triángulo
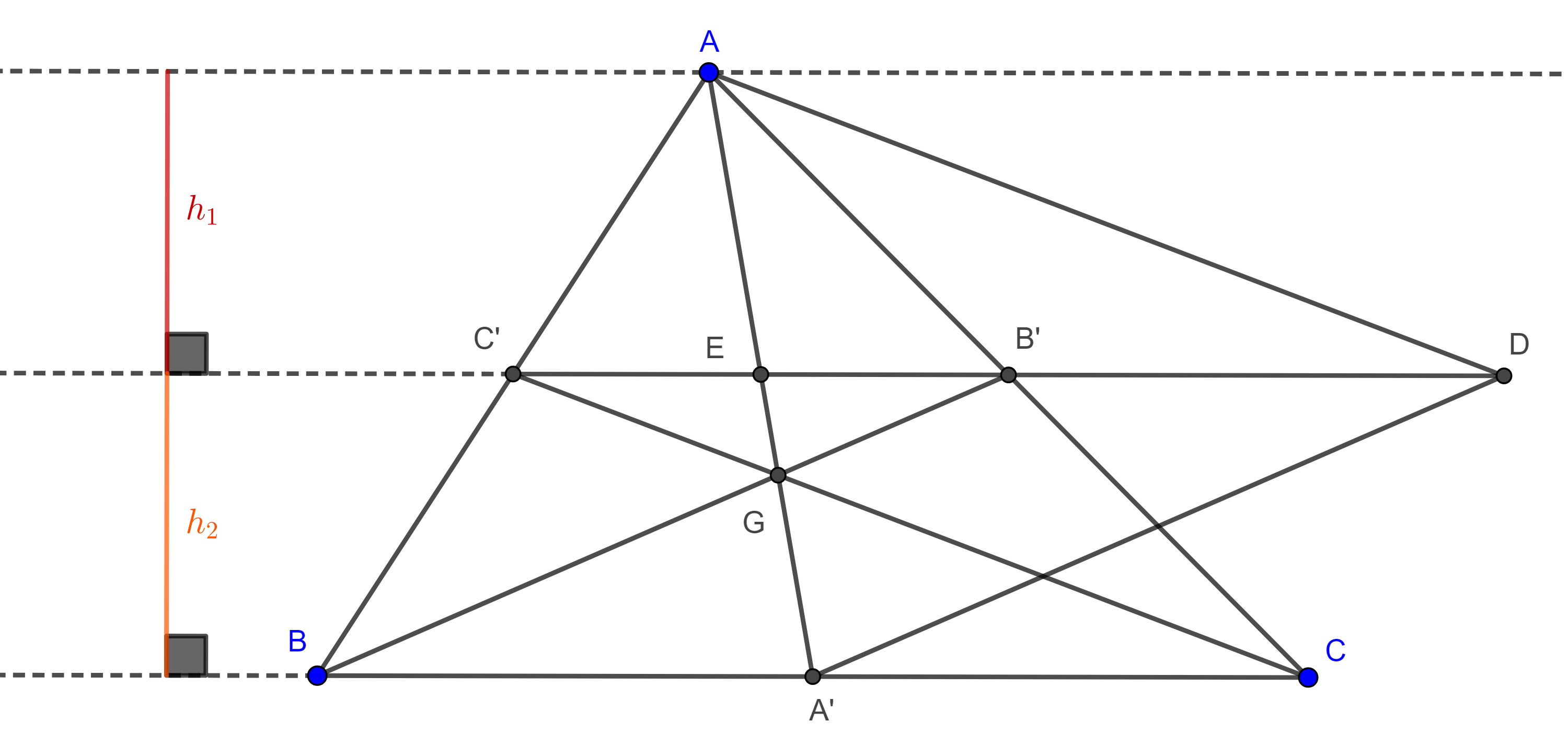
Teorema 1. Si con las medianas de un triángulo dado construimos otro triangulo, entonces cada mediana del triángulo construido es igual a tres cuartos uno de los lados del triángulo dado.
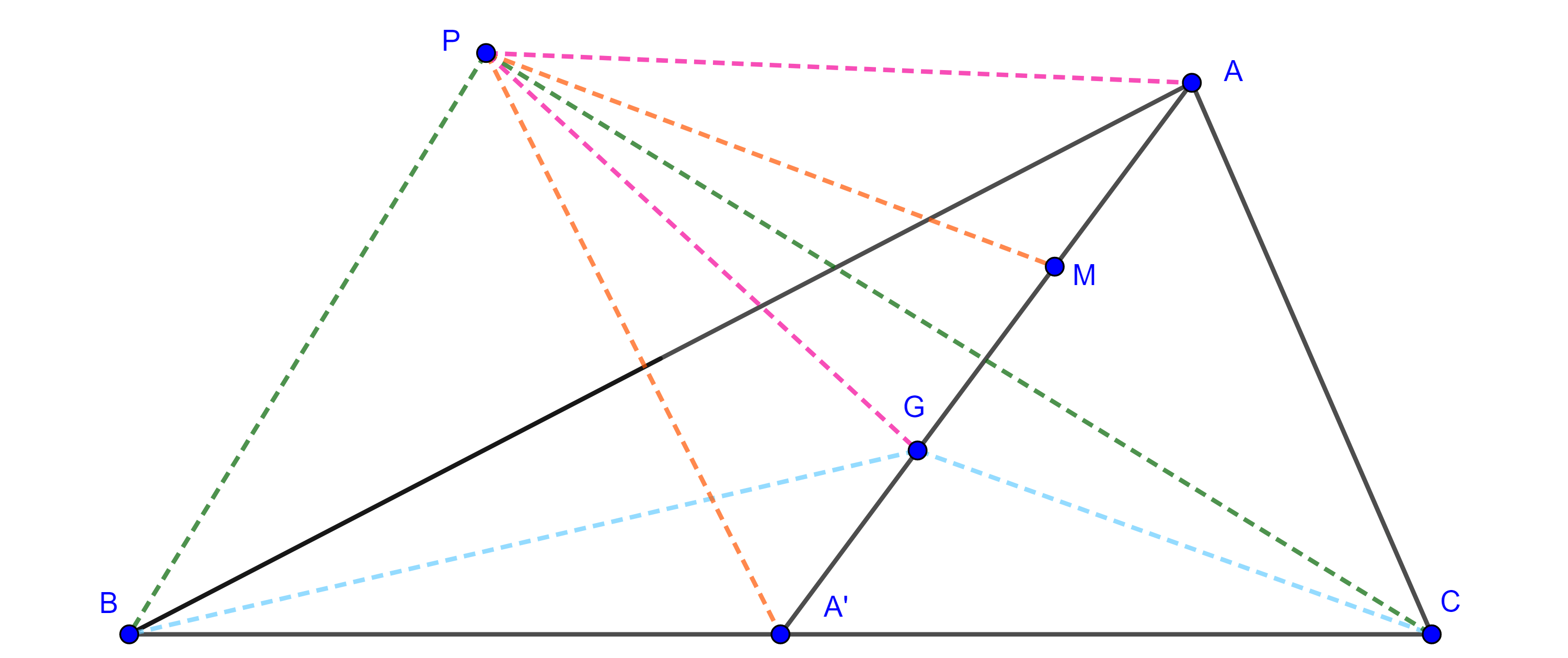
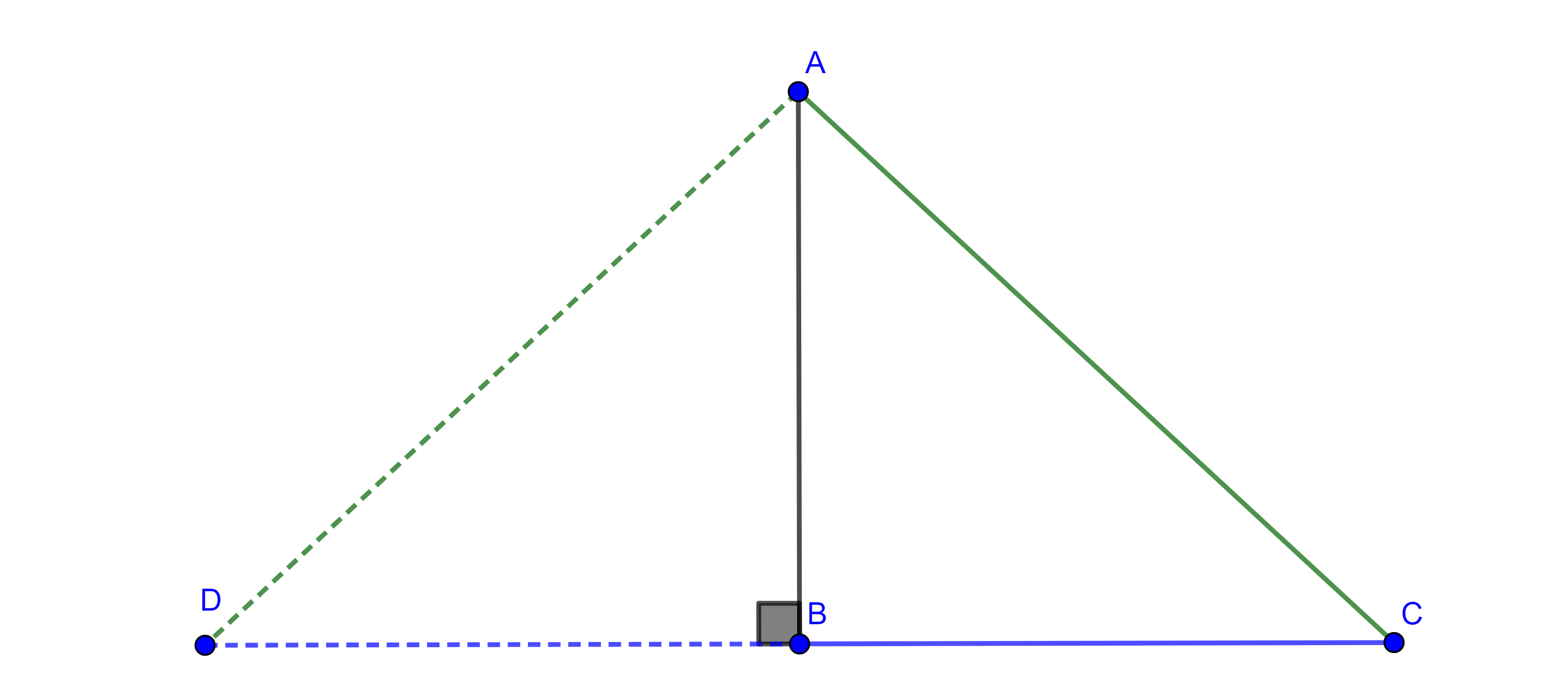
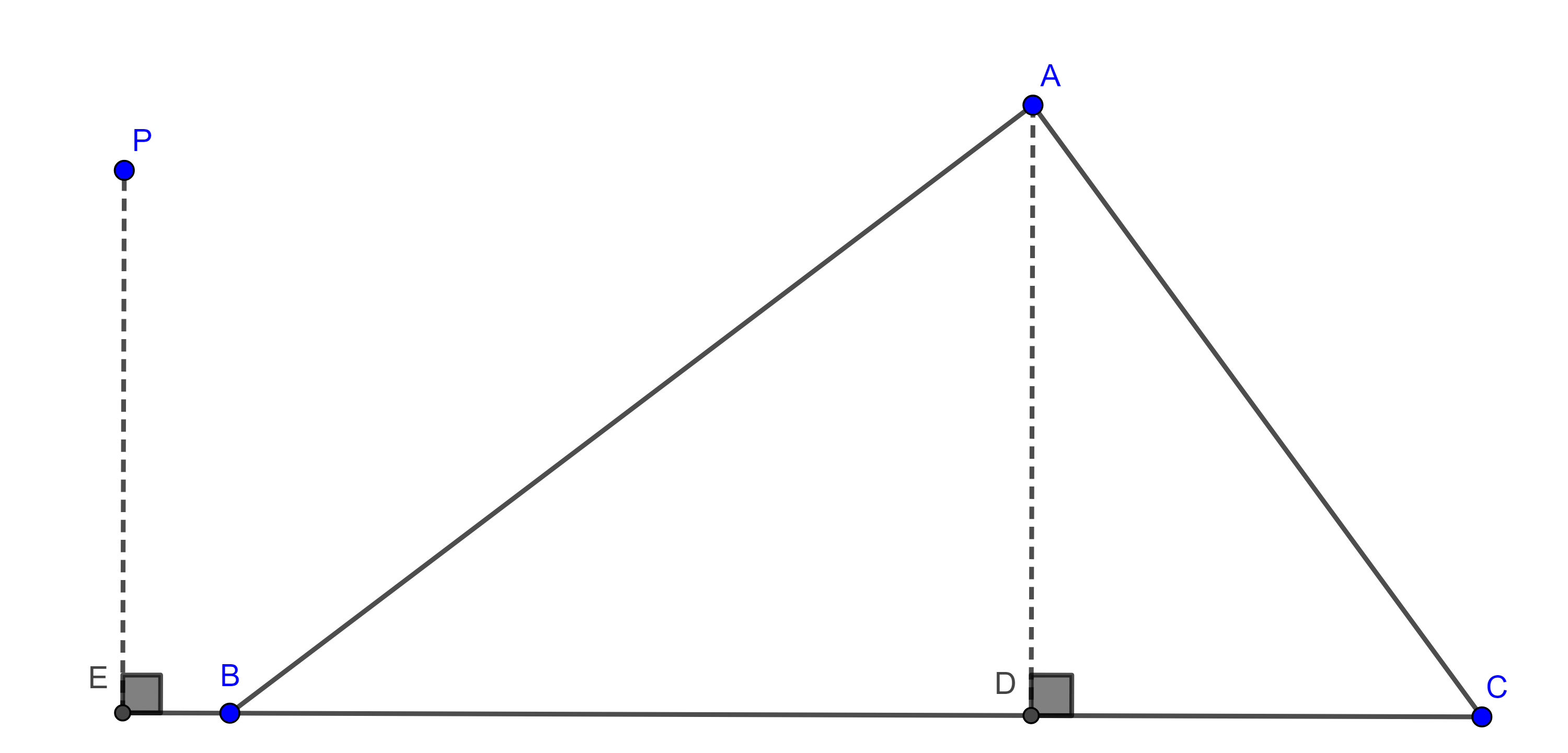
Demostración. Sean $\triangle ABC$ y $AA´$, $BB’$ y $CC’$ las medianas del triángulo.
Construimos $D \in C’B’$ tal que $C’B’ = B’D$, como $C´B´$ es un segmento medio de $\triangle ABC$ entonces $C’B’ \parallel BC$ y $2C’B’ = BC$.
Lo anterior implica que $\square B’BA’D$ es un paralelogramo y por lo tanto $BB’ = A’D$.
Como las diagonales de $\square AC’CD$ se cortan en su punto medio entonces $\square AC’CD$ es un paralelogramo, por lo tanto, $CC’ = AD$, entonces los lados de $\triangle AA’D$ son las medianas de $\triangle ABC$, por criterio LLL, cualquier otro triangulo con los mismos lados será congruente con $\triangle AA’D$.
Sea $E = AA’ \cap C’B’$, como $A’C’$ es un segmento medio de $\triangle ABC$ entonces $\square AC’A’B’$ es un paralelogramo, por lo tanto, $E$ es el punto medio de $AA’$ y de $C’B’$.
Por lo anterior tenemos que $DE$ es mediana de $\triangle ADA’$ y que $DE = \dfrac{3}{4}$, pues por construcción $C’B’ = B’D$.
Dado que $C’D = BC$ $\Rightarrow DE = \dfrac{3}{4}BC$.
Con una construcción similar podemos ver que las otras medianas de $\triangle ADA’$ son iguales a $\dfrac{3}{4}AC$ y $\dfrac{3}{4}AB$.
Observación. Notemos que si seguimos este proceso de construir triángulos con las medianas del triángulo anterior obtenemos dos grupos de triángulos semejantes, un grupo conformado por el primer, el tercer, el quinto triángulo etc. En el otro grupo estarían el segundo, el cuarto triángulo … ambos con razón de semejanza $\dfrac{3}{4}$.
$\blacksquare$
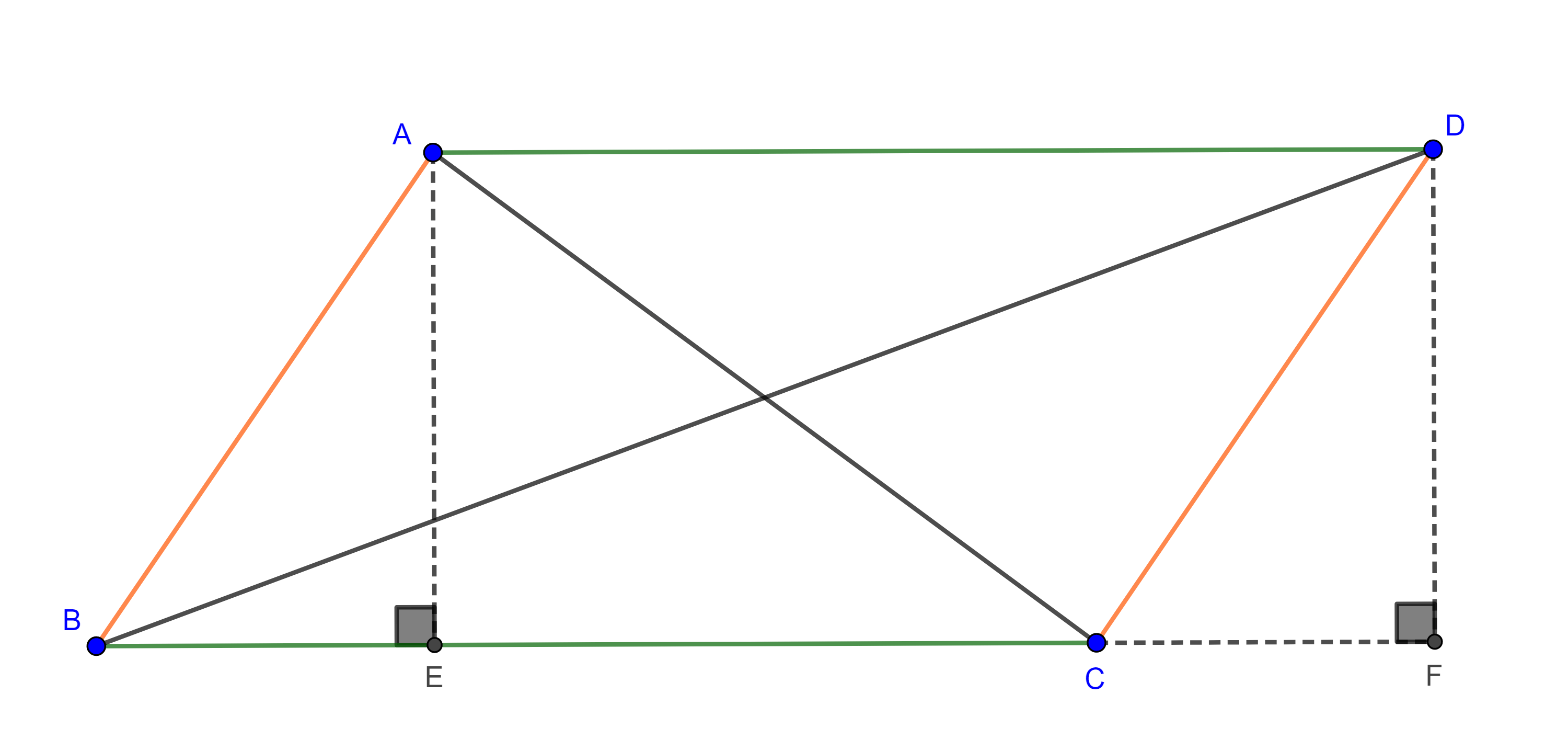
Corolario 1. El área de un triángulo construido con las medianas de un triángulo dado, es igual a tres cuartos el área del triángulo dado.
Demostración. El área de $\triangle ADA’$ (figura 1) es igual a la suma de las áreas de $\triangle EDA$ y $\triangle EDA’$ que tienen la misma base $ED$ y la suma de sus alturas es igual a la altura de $\triangle ABC$ y por el teorema 1, $DE = \dfrac{3}{4}BC$.
Por lo tanto,
$(\triangle ADA’) = (\triangle EDA) + (\triangle EDA’) = \dfrac{ED \times h_1}{2} + \dfrac{ED \times h_2}{2}$
$= \dfrac{3}{4}\dfrac{BC(h_1 + h_2)}{2} = \dfrac{3}{4}(\triangle ABC)$.
$\blacksquare$
Construcciones
Problema 1. Construir un triángulo dadas las longitudes de sus medianas $m_a$, $m_b$ y $m_c$.
Por el teorema 1, sabemos que las medianas del triángulo cuyos lados son $m_a$, $m_b$ y $m_c$, están en proporción $\dfrac{3}{4}$ a los lados del triángulo buscado.
Para encontrar las medianas del triángulo con lados $m_a$, $m_b$ y $m_c$, podemos construir este triangulo y luego sus medianas o podemos calcular sus longitudes con el teorema de Apolonio.
Después, multiplicamos cada valor obtenido por $\dfrac{4}{3}$ y así obtendremos los lados del triangulo requerido.
$\blacksquare$
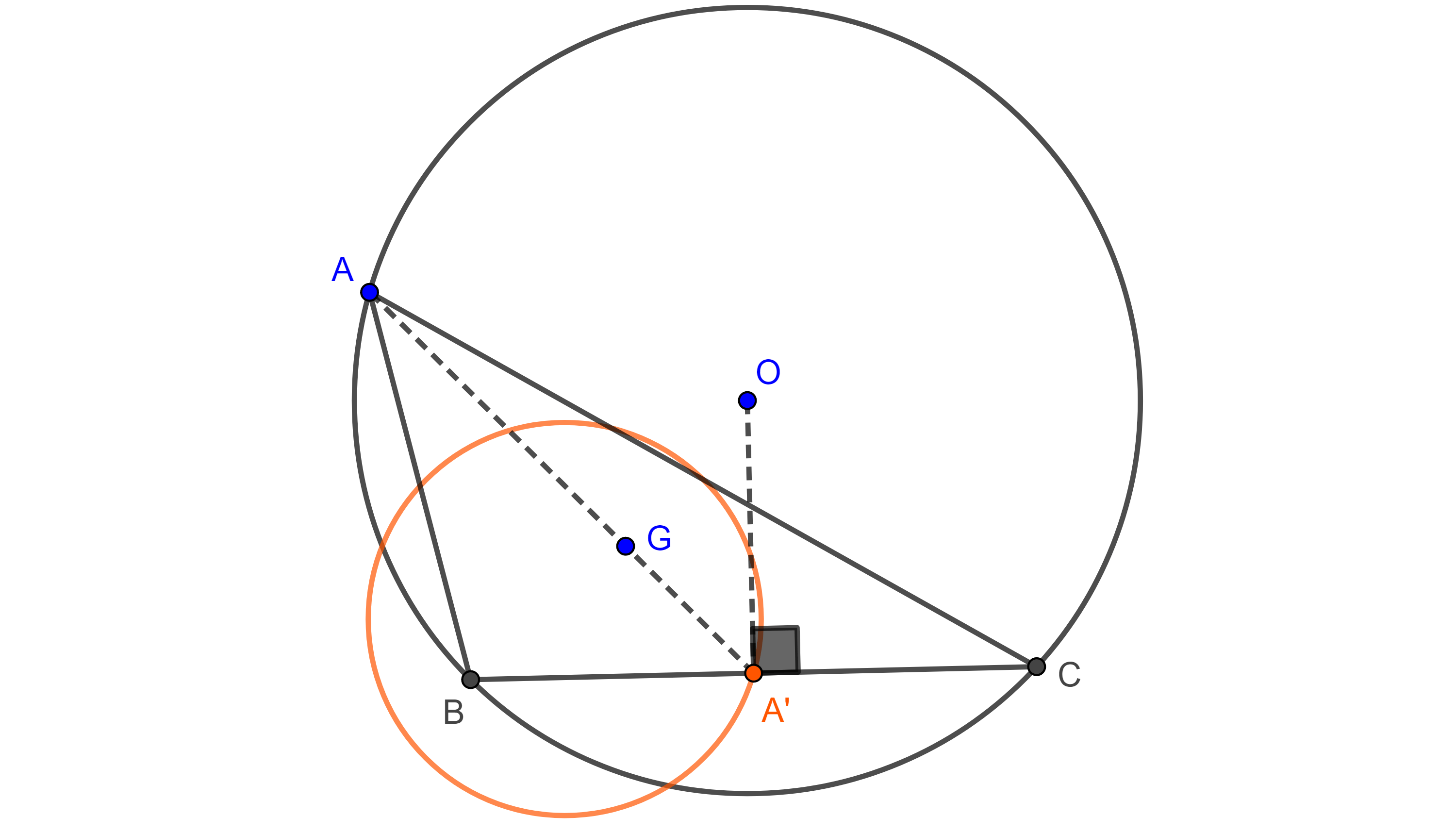
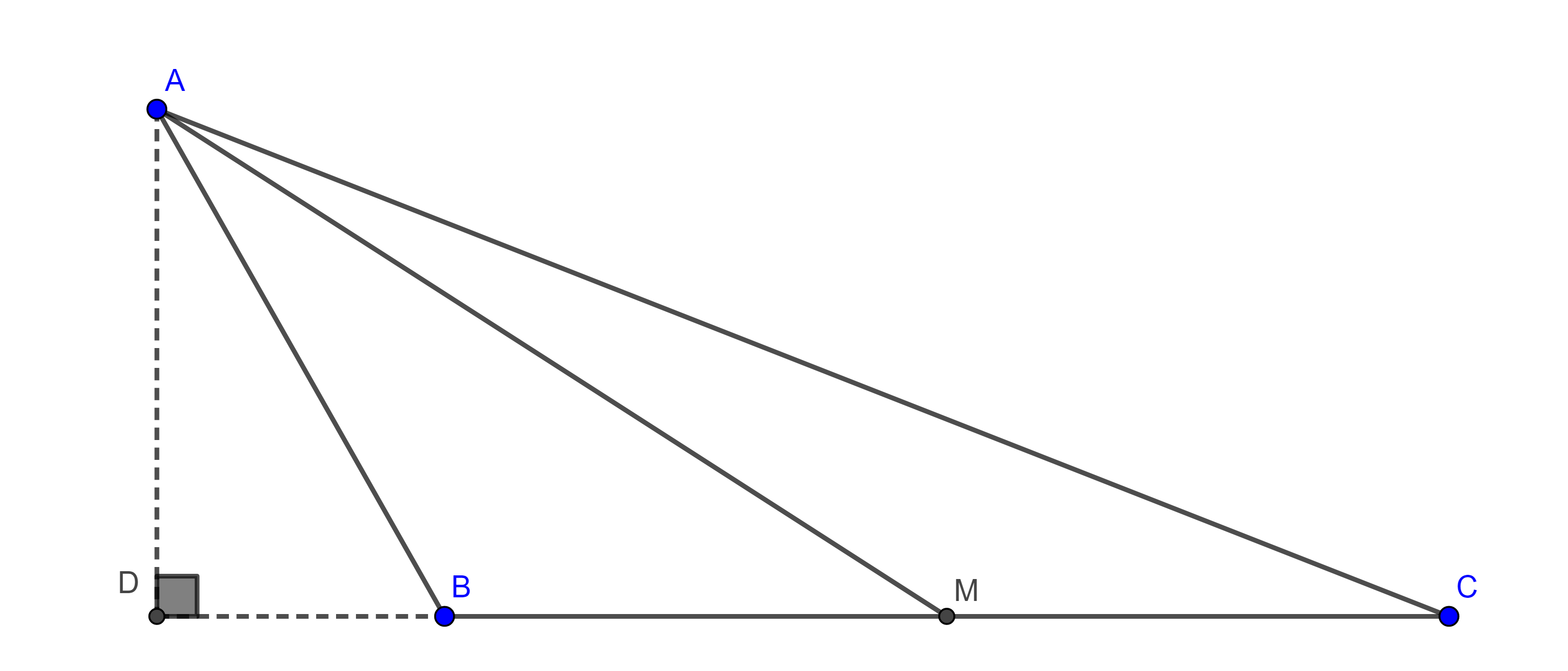
Problema 2. Dados una circunferencia y un punto dentro de esta, es posible inscribir en la circunferencia una infinidad de triángulos que tienen como centroide el punto dado.
Demostración. Sean $\Gamma(O)$ y $G$ la circunferencia y el punto dado, tomamos $A \in \Gamma(O)$, sobre la recta $AG$ construimos $A’$ tal que $GA’ = \dfrac{AG}{2}$.
Si $A’$ cae dentro de $\Gamma(O)$ por $A’$ trazamos una perpendicular a $OA’$ que interseca a $\Gamma(O)$ en $B$ en $C$, como $\triangle BOC$ es isósceles y $OA’$ es la altura por $O$, entonces $A’$ es el punto medio de $BC$.
En $\triangle ABC$ se cumple que $AA’$ es mediana y $G$ triseca a $AA’$, como el centroide de un triángulo es el único que tienen esa propiedad, entonces $G$ es el centroide de $\triangle ABC$.
Notemos que $A$ y $A’$ están en homotecia con centro en $G$ y razón $\dfrac{-1}{2}$, como $A$ describe una circunferencia, $A’$ describe una circunferencia.
Entonces hay dos posibilidades, que la homotecia de $\Gamma(O)$ este totalmente contenida dentro de ella, con lo que con cualquier punto $A$ de $\Gamma(O)$ será posible hacer la construcción previa, o la homotecia de $\Gamma(O)$ este parcialmente contenida dentro de $\Gamma(O)$ y solo con un arco de $\Gamma(O)$ será posible hacer la construcción.
Finalmente, notemos que no es posible que la homotecia de $\Gamma$ se encuentre completamente fuera de esta pues $G$ es un punto interior de $\Gamma$.
$\blacksquare$
Una propiedad del centroide
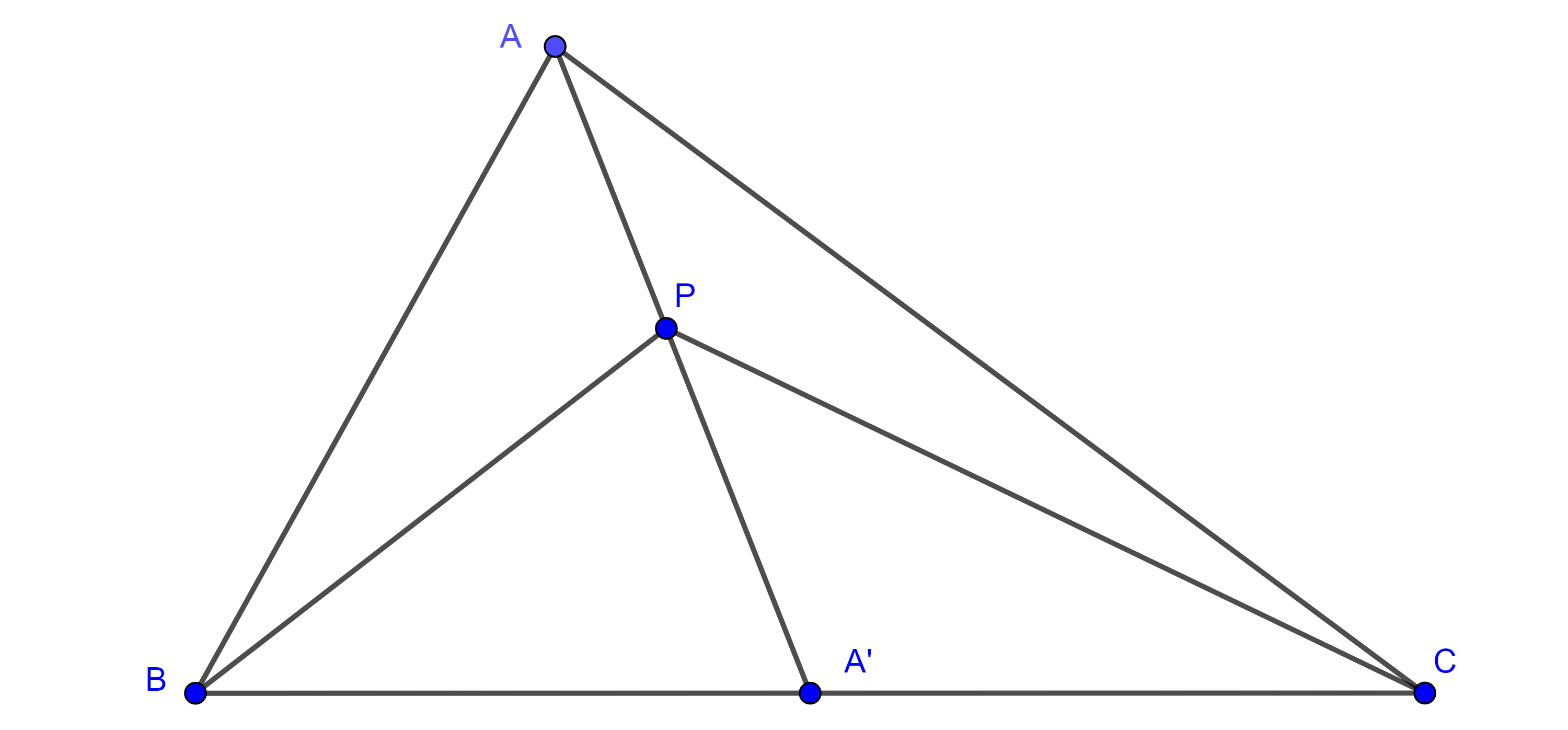
Lema. Sea $P$ un punto dentro de un triángulo $\triangle ABC$, entonces las áreas $(\triangle APB) = (\triangle APC)$ si y solo si $P$ se encuentra en la mediana $AA’$.
Demostración. Supongamos que $(\triangle APB) = (\triangle APC)$. Como $\triangle APB$ y $\triangle APC$ tienen la misma base $AP$ entonces sus alturas son iguales es decir la distancia de $B$ a $AP$ es igual a la distancia de $C$ a $AP$.
Ahora consideremos $A’ = AP \cap BC$, los triángulos $\triangle A’PB$ y $\triangle A’CP$ tienen la misma base $PA’$, por lo anterior sus alturas por B y C respectivamente también son iguales y así sus áreas son iguales $(\triangle A’PB) = (\triangle A’CP)$.
Por otro lado, para ambos triángulos, $\triangle A’PB$ y $\triangle A’CP$, la altura trazada por $P$ es la misma, esto implica que las respectivas bases son iguales, es decir $BA’ = A’C$.
Por lo tanto, $P$ está en la mediana trazada por $A$.
Recíprocamente supongamos que $P$ es un punto en la mediana $AA’$, como los pares de triángulos $\triangle BA’A$, $\triangle A’CA$ y $\triangle BA’P$, $\triangle A’CP$ tienen la misma altura desde $A$ y $P$ respectivamente, entonces
$(\triangle BA’A) = (\triangle A’CA)$ y $(\triangle BA’P) = (\triangle A’CP)$,
Por lo tanto,
$(\triangle BA’A) – (\triangle BA’P) = (\triangle A’CA) – (\triangle A’CP)$
$\Rightarrow (\triangle APB) = (\triangle APC)$.
$\blacksquare$
Teorema 2. Sea $G$ un punto dentro de un triángulo $\triangle ABC$, entonces $(\triangle AGB) = (\triangle AGC) = (\triangle BGC)$ si y solo si $G$ es el centroide de $\triangle ABC$.
Demostración. Supongamos que $(\triangle AGB) = (\triangle AGC) = (\triangle BGC)$, por el teorema anterior esto ocurre si y solo si $G$ está en la intersección de las medianas, si y solo si $G$ es el centroide de $\triangle ABC$.
$\blacksquare$
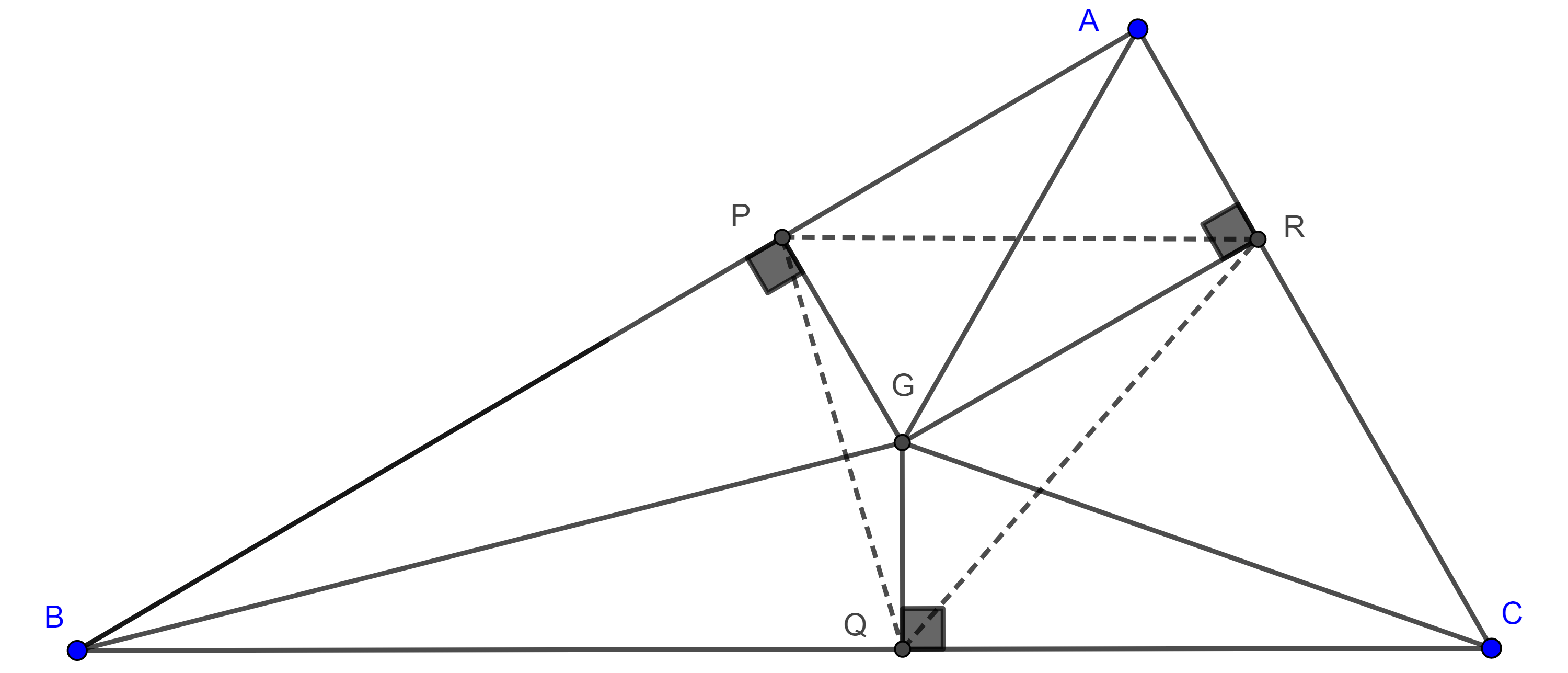
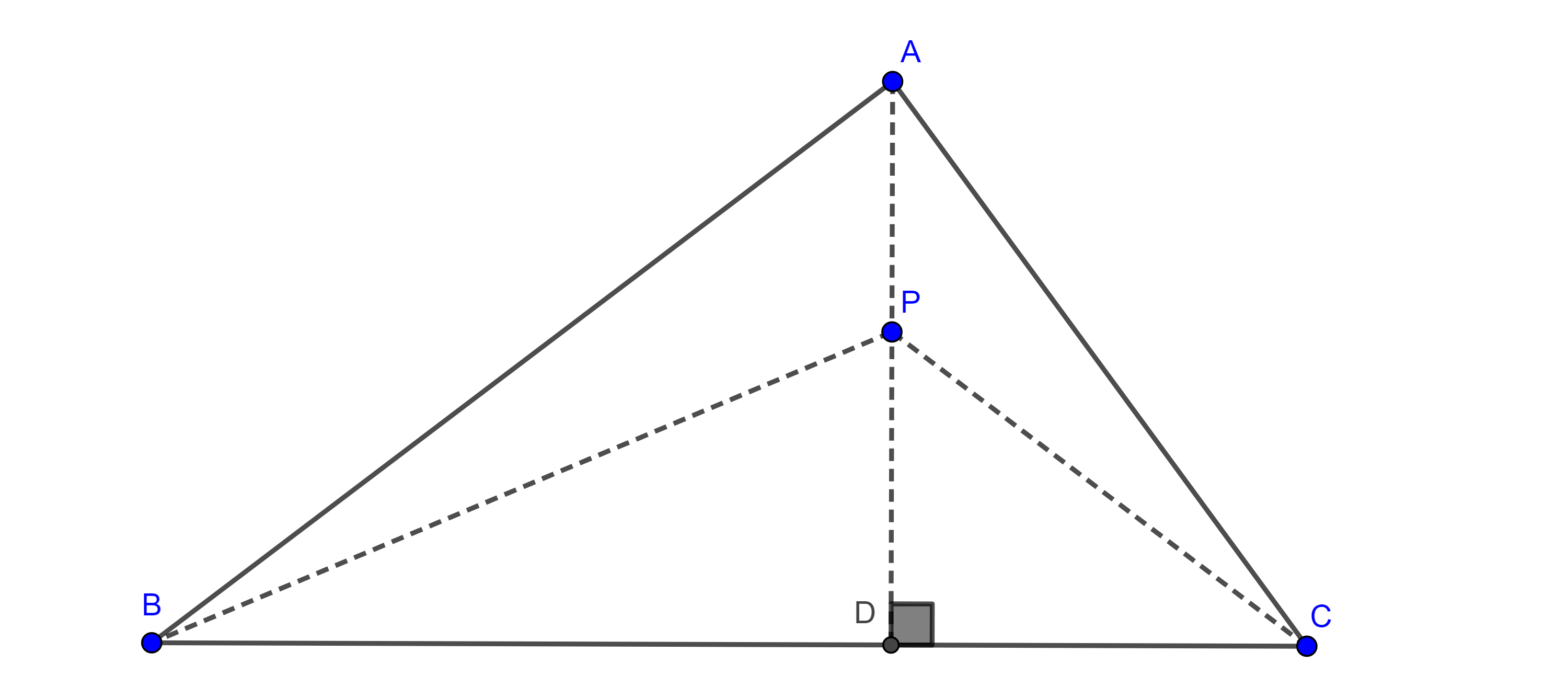
Proposición 1. Sean $\triangle ABC$ con $BC = a$, $AC = b$ y $AB = c$. Sean $G$ el centroide y $P$, $Q$, $R$ los pies de las perpendiculares desde $G$ a los lados $AB$, $BC$ y $AC$ respectivamente, entonces
$(\triangle PQR) = \dfrac{4}{9}(\triangle ABC)^3(\dfrac{a^2 + b^2 + c^2}{a^2b^2c^2})$.
Demostración. Por el teorema 3, $\triangle AGB$, $\triangle AGC$ y $\triangle BGC$ tienen la misma área, entonces
$(\triangle BGC) = \dfrac{BC \times GQ}{2}$
$\Rightarrow GQ = \dfrac{2(\triangle BGC)}{a} = \dfrac{2(\triangle ABC)}{3a}$.
De manera análoga tenemos que
$GP = \dfrac{2(\triangle ABC)}{3c}$ y $GR = \dfrac{2(\triangle ABC)}{3b}$.
Notemos que en $\square PBQG$, $\angle P + \angle Q = \pi$, en consecuencia tenemos que
$\angle G + \angle B = \pi$
$\Rightarrow \sin \angle PGQ = \sin \angle B$
Recordemos que podemos calcular el área de $\triangle ABC$ con la formula $\dfrac{ac \sin \angle B}{2}$.
Ahora calculamos
$(\triangle PGQ) = \dfrac{GP \times GQ \sin \angle B}{2}$
$= \dfrac{4(\triangle ABC)^2}{9ac} \dfrac{(\triangle ABC)}{ac}$
$= \dfrac{4(\triangle ABC)^3}{9a^2c^2}$.
De lo anterior se sigue que
$(\triangle PQR) = (\triangle PGQ) + (\triangle QGR) + (\triangle RGP)$
$= \dfrac{4(\triangle ABC)^3}{9a^2c^2} + \dfrac{4(\triangle ABC)^3}{9a^2b^2} + \dfrac{4(\triangle ABC)^3}{9b^2c^2}$
$= \dfrac{4}{9}(\triangle ABC)^3(\dfrac{a^2 + b^2 + c^2}{a^2b^2c^2})$.
$\blacksquare$
Distancia entre el centroide y el circuncentro
Teorema 3. Sean $\triangle ABC$, $G$ su centroide y $P$ un punto en el plano, entonces tenemos la siguiente igualdad
$PA^2 + PB^2 + PC^2 = GA^2 + GB^2 + GC^2 + 3PG^2$.
Demostración. Consideremos $A’$ y $M$ puntos medios de $BC$ y $AG$ respectivamente, con el teorema de Apolonio podemos calcular las medianas de los triángulos $\triangle BPC$, $\triangle A’PM$ y $\triangle GPA$ y tomemos en cuenta que $GA = MA’$.
Por lo tanto,
$PB^2 + PC^2 = 2PA’^2 + \dfrac{BC^2}{2}$,
$PG^2 + PA^2 = 2PM^2 + \dfrac{GA^2}{2}$,
$PA’^2 + PM^2 = 2PG^2 + \dfrac{MA’^2}{2} = 2PG^2 + \dfrac{GA^2}{2}$.
Sumando las tres expresiones y recordando que $GA = 2GA’$, obtenemos
$PA^2 + PB^2 + PC^2 = (PA’^2 + PM^2) + PG^2 + GA^2 + \dfrac{BC^2}{2}$
$= 2PG^2 + \dfrac{GA^2}{2} + PG^2 + GA^2 + \dfrac{BC^2}{2}$
$= 3PG^2 + GA^2 + 2GA’^2 + \dfrac{BC^2}{2}$.
Ahora aplicamos el teorema de Apolonio a $\triangle BGC$ y obtenemos
$GB^2 + GC^2 = 2GA’^2 + \dfrac{BC^2}{2}$.
Por lo tanto,
$PA^2 + PB^2 + PC^2 = 3PG^2 + GA^2 + GB^2 + GC^2$.
$\blacksquare$
Proposición 2. La suma de los cuadrados de las distancias del centroide de un triángulo a sus vértices es igual a un tercio la suma de los cuadrados de los lados del triángulo.
Demostración. Sea $\triangle ABC$ con $a = BC$, $b = AC$ y $c = AB$, con la formula para las medianas obtenemos:
$GA^2 = \dfrac{4}{9}AA’^2 = \dfrac{4}{9} (\dfrac{b^2 + c^2}{2} – \dfrac{a^2}{4})$,
$GB^2 = \dfrac{4}{9}BB’^2 = \dfrac{4}{9} (\dfrac{a^2 + c^2}{2} – \dfrac{b^2}{4})$,
$GC^2 = \dfrac{4}{9}CC’^2 = \dfrac{4}{9} (\dfrac{a^2 + b^2}{2} – \dfrac{c^2}{4})$.
Por lo tanto,
$GA^2 + GB^2 + GC^2 = \dfrac{a^2 + b^2 + c^2}{3}$.
$\blacksquare$
Corolario 2. La distancia entre el centroide $G$ y el circuncentro $O$ de un triángulo $\triangle ABC$ con circunradio $R$ se puede expresar de la siguiente forma:
$OG^2 = R^2 – (\dfrac{a^2 + b^2 + c^2}{9})$.
Demostración. Por el teorema 3 y la proposición 2 tenemos lo siguiente
$3R^2 = OA^2 + OB^2 + OC^2 = 3OG^2 + GA^2 + GB^2 + GC^2$
$= 3OG^2 + \dfrac{a^2 + b^2 + c^2}{3}$.
Despejando $OG^2$ obtenemos el resultado
$OG^2 = R^2 – (\dfrac{a^2 + b^2 + c^2}{9})$.
$\blacksquare$
Más adelante…
En la siguiente entrada estudiaremos algunas propiedades de un triangulo especial asociado a un triangulo dado, aquel que tiene como vértices los puntos medios del triangulo dado. Esto nos permitirá mostrar que el ortocentro, el centroide y el circuncentro de un triángulo siempre son colineales.
Tarea moral
A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.
- Construye un triángulo dados dos vértices y el centroide.
- Prueba que en un triángulo la recta que une el punto medio de una de sus medianas con uno de los vértices del triángulo triseca el lado opuesto al vértice considerado.
- Muestra que las medianas de un triángulo dividen al triangulo en seis triángulos que tienen la misma área.
- Demuestra que en un triangulo,
$i)$ entre cualesquiera dos de sus medianas la menor de ellas biseca al lado mas grande,
$ii)$ si dos de sus medianas son iguales entonces el triangulo es isósceles. - Sean $\triangle ABC$ y $AA’$, $BB’$, $CC’$ sus medianas, muestra que $\frac{3}{4}(AB^2 + BC^2 + AC^2) = AA’^2 +BB’^2 + CC’^2$.
- Sea $\triangle ABC$ con medianas $AA’$, $BB’$ y $CC’$, sean $m = AA’ + BB’ + CC’$ y $s = AB + BC + CA$, muestra que $\frac{3}{2}s > m > \frac{3}{4}s$.
Entradas relacionadas
- Ir a Geometría Moderna I.
- Entrada anterior del curso: Desigualdades geométricas.
- Siguiente entrada del curco: Triángulo medial y recta de Euler.
- Otros cursos.
Fuentes
- Altshiller, N., College Geometry. New York: Dover, 2007, pp 65-71.
- Gomez, A. y Bulajich, R., Geometría. México: Instituto de Matemáticas, 2002, pp 80-84.
- Posamentier, A. y Salkind, C; Challenging Problems in Geometry. New York: Dover, 1996, pp 14.
Agradecimientos
Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»