Introducción
En la entrada anterior se revisó el concepto de continuidad en un punto, así como algunas de sus propiedades. Además, se definió la continuidad en un intervalo, concepto que se empleará en esta entrada para probar uno de los resultados más relevantes para las funciones continuas: el teorema del valor intermedio.
Idea intuitiva
Este teorema nos dice que para una función continua en determinado intervalo $[a,b]$, si el valor de $f$ al evaluarla en $a$ cambia de signo con respecto al valor que se obtiene al evaluarla en $b$, entonces existe algún punto $x$ tal que al evaluar la función en dicho punto, toma el valor de cero.
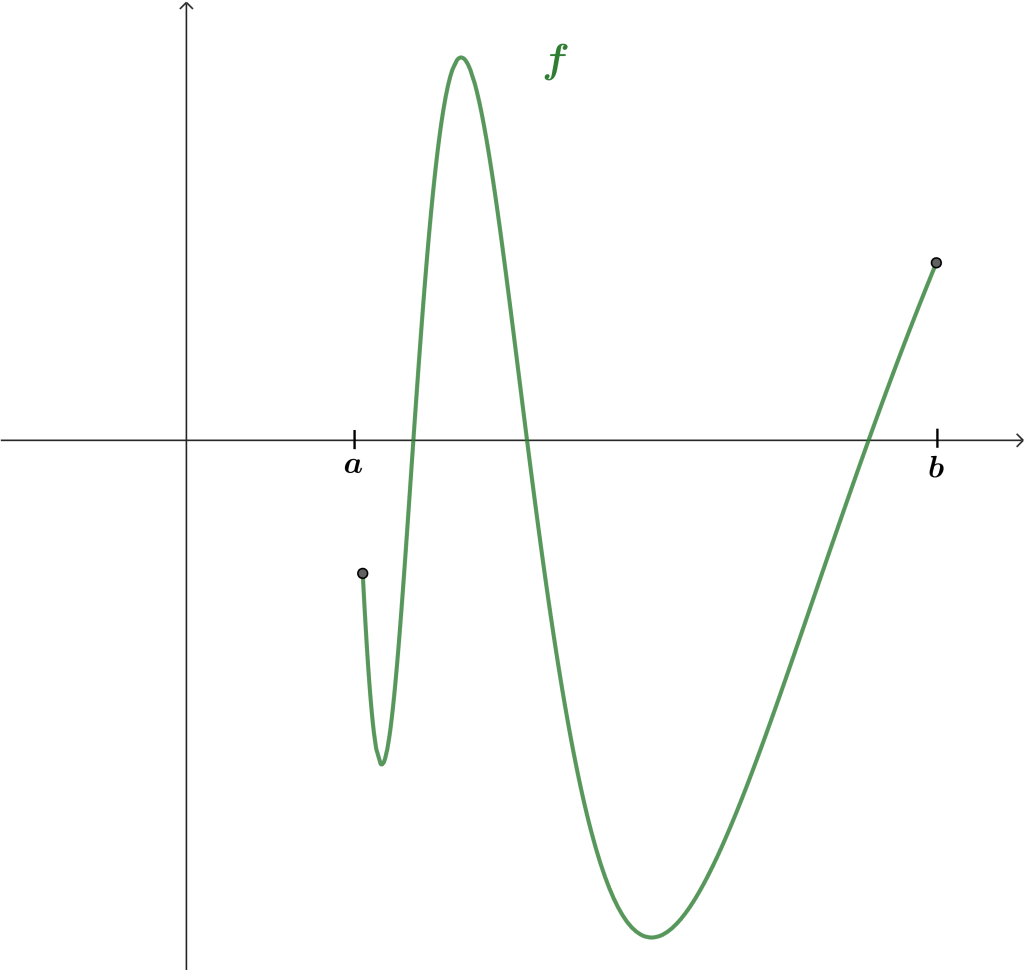
Recordemos la idea intuitiva de continuidad, una función es continua si puedes dibujarla sin soltar el lápiz; pensemos en el caso particular que $f(a) < 0$ y $f(b) > 0$. En la siguiente imagen se muestra una función continua que pasa por ambos.
¿Podrías dibujar una función continua que pase por ambos puntos sin pasar por $0$ en el eje horizontal? Probaremos que esto no es posible en el siguiente teorema; pero antes desarrollemos la intuición de lo que debe suceder. Para ello, recordemos el último teorema revisado en la entrada anterior.
Teorema. Supongamos que $f$ es continua en $x_0$ y $f(x_0)>0$. Entonces $f(x) >0$ para todo $x$ en un intervalo que contiene a $x_0$, es decir, existe $\delta > 0$ tal que $f(x) >0$ para todo $x$ tal que $|x-x_0|< \delta$.
De forma análoga, si $f(x_0) <0$, entonces existe $\delta > 0$ tal que $f(x) < 0$ para todo $x$ tal que $|x-x_0|< \delta$.
Es decir, si una función continua toma un valor positivo en un punto $x_0$, entonces debe suceder que es positiva en todo un intervalo: $(x_0-\delta, x_0+\delta)$. Análogamente, si la función es negativa en determinado punto, entonces debe suceder que es negativa en todo un intervalo. Así, podemos pensar en el intervalo más grande que captura el comportamiento negativo (o positivo), ¿en qué punto se termina? Para responder esta pregunta, haremos uso de un concepto revisado anteriormente, el supremo.
Teorema del valor intermedio
Teorema del valor intermedio. Sea $f:[a,b] \to \mathbb{R}$ continua en todo el intervalo $[a,b]$. Si $f(a) < 0$ y $f(b) > 0,$ entonces existe $c$, $a<c<b,$ tal que $f(c) = 0$.
Demostración.
Como $f(a) < 0$, sabemos que existe $\delta_1$ tal que para todo $x \in (a – \delta_1, a + \delta_1) \cap [a,b]$ se tiene que $f(x) < 0$. Es decir,
$$\forall x \in [a, a+\delta_1), \quad f(x) <0. \tag{1}$$
Como $f(b) > 0$, sabemos que existe $\delta_2$ tal que para todo $x \in (b – \delta_2, b + \delta_2) \cap [a,b]$ se tiene que $f(x) > 0$. Es decir,
$$\forall x \in (b-\delta_2,b], \quad f(x) > 0. \tag{2}$$
Definamos ahora el siguiente conjunto:
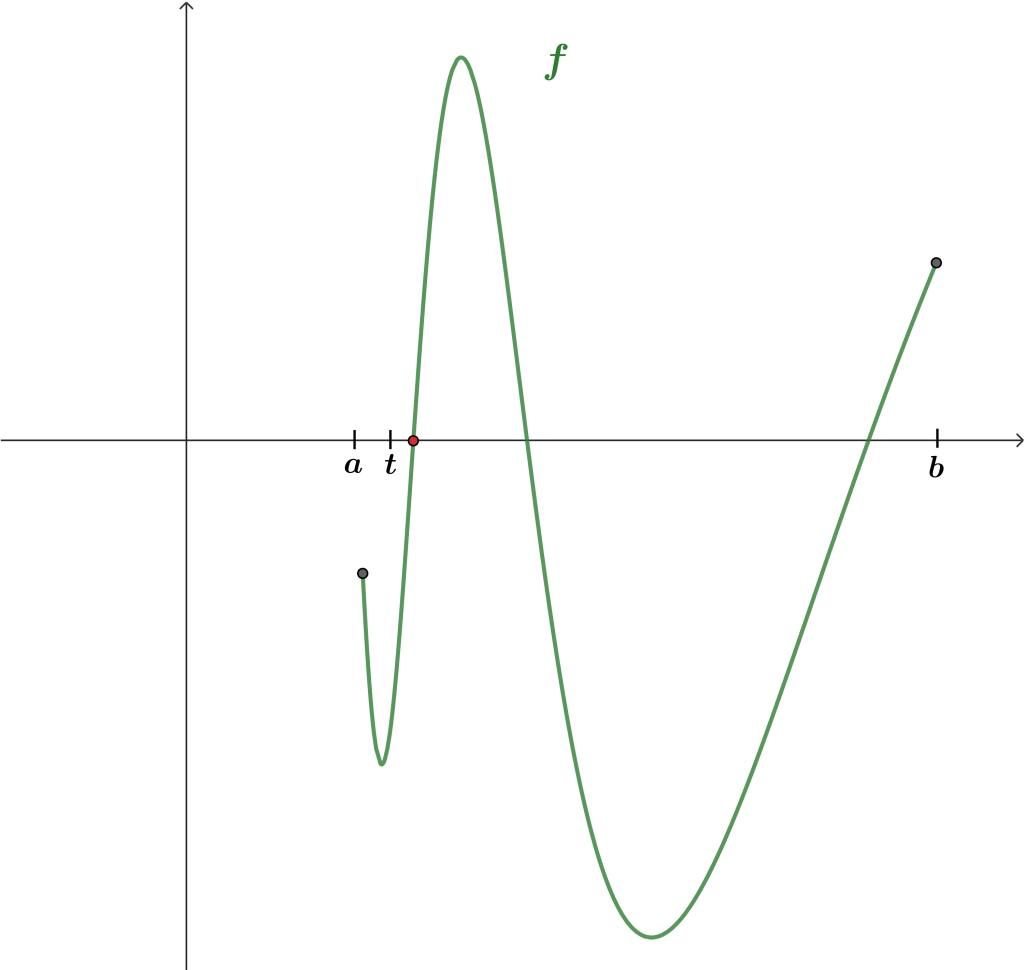
$$A = \{ t \in [a,b] \quad | \quad \forall x \in [a, t], f(x) < 0 \}.$$
Es decir, el conjunto $A$ está formado por todos los números reales que forman un intervalo $[a, t]$ donde $f$ toma valores negativos. Utilizando la ilustración del inicio, se puede ejemplificar cómo se ve $t$, que estará en el eje $x$ entre $a$ y el punto rojo marcado.
Primero veamos que $A \neq \varnothing$.
Consideremos $t_0 = a + \frac{\delta_1}{2}$. Es inmediato que $a< a + \frac{\delta_1}{2} < a +\delta_1 $ y como $[a, a + \frac{\delta_1}{2}] \subset [a, a+\delta_1)$, por $(1)$ se tiene que, para todo $x \in [a, a + \frac{\delta_1}{2}]$, $f(x) < 0$.
$$\therefore t_0 \in A \Rightarrow A \neq \emptyset.$$
Notemos que el conjunto $A$ está acotado. Por definición si $t \in A$, entonces $t \in [a,b]$, es decir, $t \leq b$. Ahora, como nuestro conjunto $A$ es no vacío y está acotado, sí tiene supremo. Sea $\alpha = supA$.
Adicionalmente, notemos que
- $t_0 = a+\frac{\delta_1}{2} \in A$ y $a+\frac{\delta_1}{2} \leq \alpha \leq b$.
- Por $(2)$, para todo $x \in (b-\delta_2, b]$ se tiene que $f(x) >0$, entonces $\alpha \leq b-\delta_2$.
Por lo anterior, se tiene
\begin{gather*}
& a< a+\frac{\delta_1}{2} \leq \alpha \leq b-\delta_2 < b.
\end{gather*}
Se sigue que $a<\alpha<b.$
Para finalizar con la prueba, demostraremos que $f(\alpha) = 0$.
Para demostrarlo procederemos por contracción, es decir, supongamos que $f(\alpha) \neq 0$, entonces existen dos casos, $f(\alpha) > 0$ ó $f(\alpha) < 0$.
- Caso 1: $f(\alpha) < 0$.
Se tiene que $f(\alpha) < 0$, entonces existe $\delta_3$ tal que para todo $x \in (\alpha – \delta_3, \alpha + \delta_3) \cap [a,b]$ se cumple que $f(x) < 0$.
Dado que $\alpha = supA \quad$ y $\quad \alpha – \delta_3 < \alpha$, entonces existe $t \in A$ tal que $\alpha-\delta_3 < t \leq \alpha$. Adicionalmente, consideremos $s$ tal que $\alpha < s < \alpha + \delta_3$ y $s <b$.
Como $[t, s] \subset (\alpha – \delta_3, \alpha + \delta_3)$, entonces
$$\forall x \in [a,s], \quad f(x) < 0.$$
Además, por definición del conjunto A, para todo $x \in [a,t]$ se tiene $f(x) < 0$. Entonces
$$\forall x \in [a,s] = [a,t] \cup [t,s], \quad f(x) < 0.$$
Entonces $s \in A$ y $\alpha < s$, lo cual es una contradicción pues $\alpha$ es el supremo de $A$.
$$\therefore f(\alpha) \geq 0.$$
- Caso 2: $f(\alpha) > 0$.
Dado que $f$ es continua en $\alpha$, entonces existe $\delta_4 > 0$ tal que para todo $x \in (\alpha – \delta_4, \alpha + \delta_4)$, $f(x) > 0$.
Como $\alpha – \delta_4 < \alpha$, entonces existe $t \in A$ tal que $\alpha – \delta_4 < t \leq \alpha$. Como $t \in A$, entonces $f(t) < 0$ y como $\alpha – \delta_4<t \leq \alpha < \alpha + \delta$, $f(t) >0$, lo cual es una contradicción.
Por tanto, $f(\alpha) = 0$.
Así, consideremos $c = \alpha$, $a<c<b$ y $f(c) = 0.$
$\square$
Podemos notar que el teorema no solo vale cuando la función va de negativo ($f(a) < 0$) a positivo ($f(b) > 0$), sino también en el caso inverso ($f(a) > 0$ y $f(b) < 0$) y lo probaremos en el siguiente corolario.
Corolario. Sea $f: [a, b] \to \mathbb{R}$, continua en $[a, b]$. Si $f(a) > 0$ y $f(b) < 0$, entonces existe $c$, $a<c<b$, tal que $f(x) = c$.
Demostración.
Consideremos la función $h: [a, b] \to \mathbb{R}$, $h(x) = -f(x).$
Notemos que $h$ es continua pues $f$ lo es. Además $h(a) = -f(a) <0$ y $h(b) = -f(b) >0$. Aplicando el teorema del valor intermedio, existe $c$ que cumple $a<c<b$ tal que
\begin{gather*}
h(c) = 0.
\end{gather*}
Se sigue que
\begin{gather*}
& -f(c) = 0. \\
\therefore & f(c) = 0.
\end{gather*}
$\square$
Más aún, si en un intervalo $[a, b]$ se cumple que $f(a) < M$ y $f(b) > M$, entonces también existe un punto $c$ tal que $f(c) = M$.
Corolario. Sea $M \in \mathbb{R}$, si $f(a) < M$ y $f(b) > M$. Entonces existe $c$, $a<c<b$, tal que $f(c) = M$.
Demostración.
Consideremos la función $h:[a,b] \to \mathbb{R}$, con $h(x) = f(x)-M$.
Notemos que $h$ es continua. Además $h(a) = f(a)-M < 0$ y $h(b) = f(b)-M > 0$. Por el teorema del valor intermedio, existe $c$, $a<c<b$, tal que $h(c) = 0$. Entonces $f(c)-M = 0$.
$$\therefore f(c) = M.$$
$\square$
Análogamente, tenemos el siguiente resultado.
Corolario. Sea $M \in \mathbb{R}$, si $f(a) >M$ y $f(b) < M$. Entonces existe $c$, $a<c<b$, tal que $f(c) = M$.
Más adelante…
En la siguiente entrada demostraremos otra propiedad fuerte respecto a las funciones continuas: si una función es continua en un intervalo, entonces está acotada. Más aún, existe un valor $x_0$ en el intervalo tal que la función alcanza su máximo en dicho punto. De forma análoga, existe un punto en el que la función alcanza su mínimo.
Tarea moral
A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.
- Sea $f$ continua en el intervalo $[0,1]$ y tal que $f(0) = f(1)$. Demostrar que existe un punto $c \in [0, \frac{1}{2}]$ tal que $f(c) = f(c + \frac{1}{2}).$
- Sea $M \in \mathbb{R}$, si $f(a) >M$ y $f(b) < M$. Prueba que existe $c$, $a<c<b$ tal que $f(c) = M.$
- Dado $f(x) = x^2 + 2x – 7$, demuestra que existe $c$ tal que $f(c) = 50.$
- Para la ecuación $2x^7= x-1$, encuentra una solución en $[0,1].$
Entradas relacionadas
- Ir a Cálculo Diferencial e Integral I
- Entrada anterior del curso: Definición de continuidad y sus propiedades
- Siguiente entrada del curso: Funciones acotadas y teorema del máximo-mínimo
- Resto de cursos: Cursos
Agradecimientos
Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»