Introducción
Continuando ahora con las funciones crecientes y decrecientes, veremos qué condiciones se deben cumplir para determinar si una función crece o decrece en un intervalo. De igual manera, veremos cuándo una función es no creciente o no decreciente para finalizar con la definición de función acotada.
Definición de función creciente y decreciente
Definición: Sea $f: A \rightarrow B$ una función con $A , B \subseteq \RR$.
- Decimos que $f$ es una función creciente si y sólo si para cualesquiera $x_{1}, x_{2} \in A$ tales que
$$x_{1}< x_{2} \Rightarrow f(x_{1})<f(x_{2})\quad\text{.}$$ - Decimos que $f$ es una función decreciente si y sólo si para cualesquiera $x_{1}, x_{2} \in A$ tales que
$$x_{1}< x_{2} \Rightarrow f(x_{2})<f(x_{1})\quad\text{.}$$
Definición de función no creciente y no decreciente
Definición: Consideremos a la función $f: A \rightarrow B$.
- Llamamos a $f$ una función no creciente (que decrece o permanece igual) si y sólo si para cualesquiera $x_{1}, x_{2} \in A$ que cumplen
$$x_{1}< x_{2} \Rightarrow f(x_{2})\leq f(x_{1})\quad\text{.}$$ - Llamamos a $f$ una función no decreciente (que crece o permanece igual) si y sólo si para cualesquiera $x_{1}, x_{2} \in A$ que cumplen
$$x_{1}< x_{2} \Rightarrow f(x_{1})\leq f(x_{2})\quad\text{.}$$
Ejemplo 1
Veamos que para la función definida como:
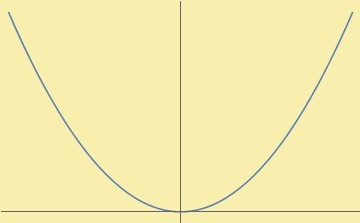
$$f(x)=x^{2}$$
Tenemos las siguientes observaciones:
- Es creciente en el intervalo $[0, \infty)$.
- Es decreciente en el intervalo $(- \infty,0)$.
Demostración:
- Sea $0 \leq x_{1} < x_{2}$ así se sigue que:
\begin{align*}
&\Rightarrow x_{1}^{2} < x_{2}^{2}\\
&\Rightarrow f(x_{1}) < f(x_{2})
\end{align*}
$\therefore f$ es creciente en $[0, \infty)$. - Ahora tomemos $x_{1} < x_{2} < 0$
\begin{align*}
&\Rightarrow 0< -x_{2} <-x_{1}\tag{ Multiplicando por $-1$}\\
&\Rightarrow f(-x_{2})<f(-x_{1})\tag{por 1.}\\
&\Rightarrow (-x_{2})^{2} <(-x_{1})^{2}\\
&\Rightarrow x_{2}^{2} < x_{1}^{2}\\
&\Rightarrow f(x_{2})<f(x_{1})
\end{align*}
$\therefore f$ es decreciente en $(- \infty,0)$.
$\square$
Ejemplo 2
Para la función $g(x)= x^{2}-5x+2$ probaremos que es creciente en el intervalo $[0,\infty)$.
Tomemos $x_{1}, x_{2} \in [0,\infty)$ tales que $x_{1} < x_{2}$. Queremos demostrar que $g(x_{1})<g(x_{2})$ por lo que desarrollamos lo siguiente:
\begin{align*}
x_{1} < x_{2} &\Rightarrow x_{1} – 5 < x_{2}-5 \tag{restando $-5$}\\
&\Rightarrow x_{1}(x_{1} – 5) <x_{2}( x_{2}-5) \tag{multiplicando por $x_{1}$ y $x_{2}$}\\
&\Rightarrow x_{1}^{2} – 5x_{1} < x_{2}^{2}-5x_{2}\\
&\Rightarrow x_{1}^{2} – 5x_{1}+2 < x_{2}^{2}-5x_{2}+2 \tag{sumado $2$}\\
&\Rightarrow g(x_{1})<g(x_{2})
\end{align*}
Así concluimos que $g$ es creciente en el intervalo $[0,\infty)$.
$\square$
Algunos teoremas
Teorema: Sean $f,g: D \subseteq \r \rightarrow \r$ si $f$ y $g$ son crecientes en $D$ tales que
$f(x)>0$ y $g(x) >0$ para todo $x \in D \Rightarrow fg$ es creciente en D.
Demostración:
Tomemos $x_{1}, x_{2} \in D$ tales que $x_{1}<x_{2}$. Queremos probar que:
$$(fg)(x_{1})< (fg)(x_{2})\quad\text{.}$$
Es decir, queremos ver que se cumple la siguiente desigualdad:
$$f(x_{1})g(x_{1})< f(x_{2})g(x_{2})\quad\text{.}$$
Observemos que por hipótesis tenemos que se cumplen para todo $x \in D$ las siguientes desigualdades:
- $f(x)>0 \quad$ y $\quad g(x)>0$.
- $f(x_{1}) < f(x_{2})$ ya que $f$ es creciente.
- $g(x_{1}) < g(x_{2})$ ya que $g$ es creciente.
De los puntos 2 y 3 al realizar el producto obtenemos:
$$f(x_{1})g(x_{1})< f(x_{2})g(x_{2})\quad\text{.}$$
$\square$
Teorema: Si tenemos una función $f$ tal que:
- $f$ par y creciente en el intervalo $[0, \infty) \Rightarrow f$ es decreciente en $(-\infty, 0)$.
- $f$ par y decreciente en el intervalo $[0, \infty) \Rightarrow f$ es creciente en $(-\infty, 0)$.
- $f$ impar y creciente en el intervalo $[0, \infty) \Rightarrow f$ es creciente en $(-\infty, 0)$.
- $f$ impar y decreciente en el intervalo $[0, \infty) \Rightarrow f$ es decreciente en $(-\infty, 0)$.
La demostración de los puntos 1,2 y 3 se dejarán como ejercicios para el lector en la Tarea moral de esta entrada.
Demostración del punto 4:
Queremos probar que $f$ es decreciente en $(-\infty, 0)$.
Tenemos por hipótesis que $f$ es una función impar, así por definición:
$$f(-x)=-f(x)\quad\text{.}$$
Ahora si tomamos $0< x_{1}<x_{2}$ ocurre que:
\begin{align*}
f(-x_{1})&= -f(x_{1}) & f(-x_{2})&= -f(x_{2})\\
\end{align*}
Vemos que si multiplicamos por $-1$ las igualdades anteriores tenemos la siguiente equivalencia:
\begin{align}
-f(-x_{1})&= f(x_{1}) & -f(-x_{2})&= f(x_{2})\\
\end{align}
Como $f$ es una función decreciente en $[0, \infty)$ para $x_{1}$ y $x_{2}$ se sigue:
$$f(x_{2})< f(x_{1})\quad\text{.}$$
Aplicando $(1)$ tendríamos la siguiente desigualdad:
$$-f(-x_{2})< -f(-x_{1})\quad\text{.}$$
donde $-x_{1},-x_{2} \in (-\infty,0)$.
$\square$
Definición de función acotada
Definición: Sea $f: A \rightarrow B$. Decimos que:
- $f$ está acotada superiormente $\Leftrightarrow$ existe $M \in \r$ tal que $f(x) \leq M$ para todo $x \in A$.
- $f$ está acotada inferiormente $\Leftrightarrow$ existe $m \in \r$ tal que $m \leq f(x)$ para todo $x \in A$.
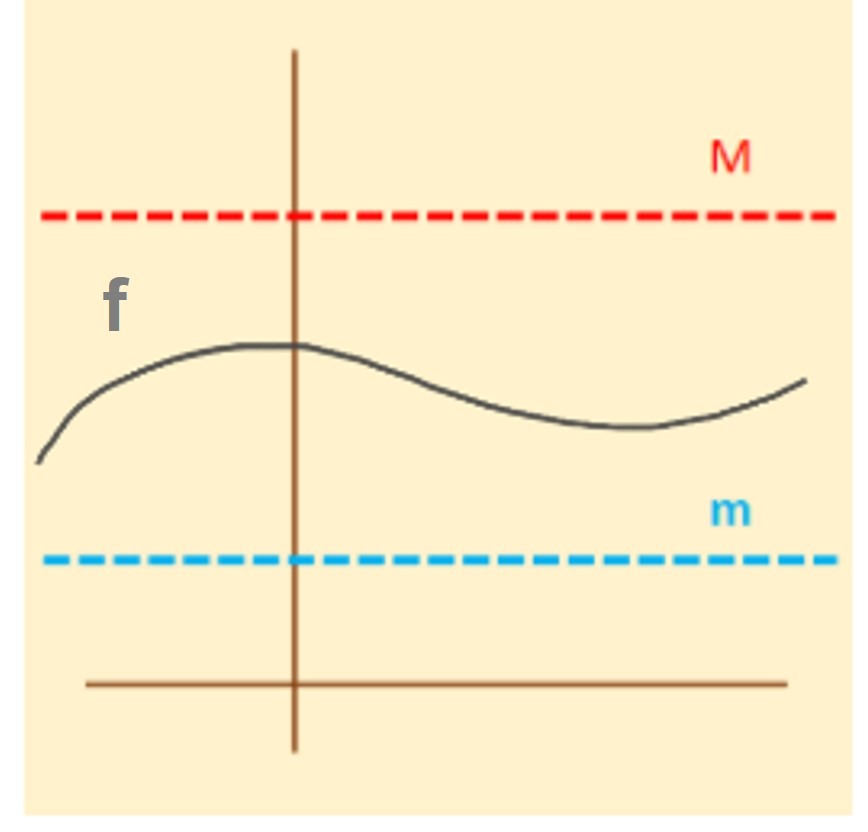
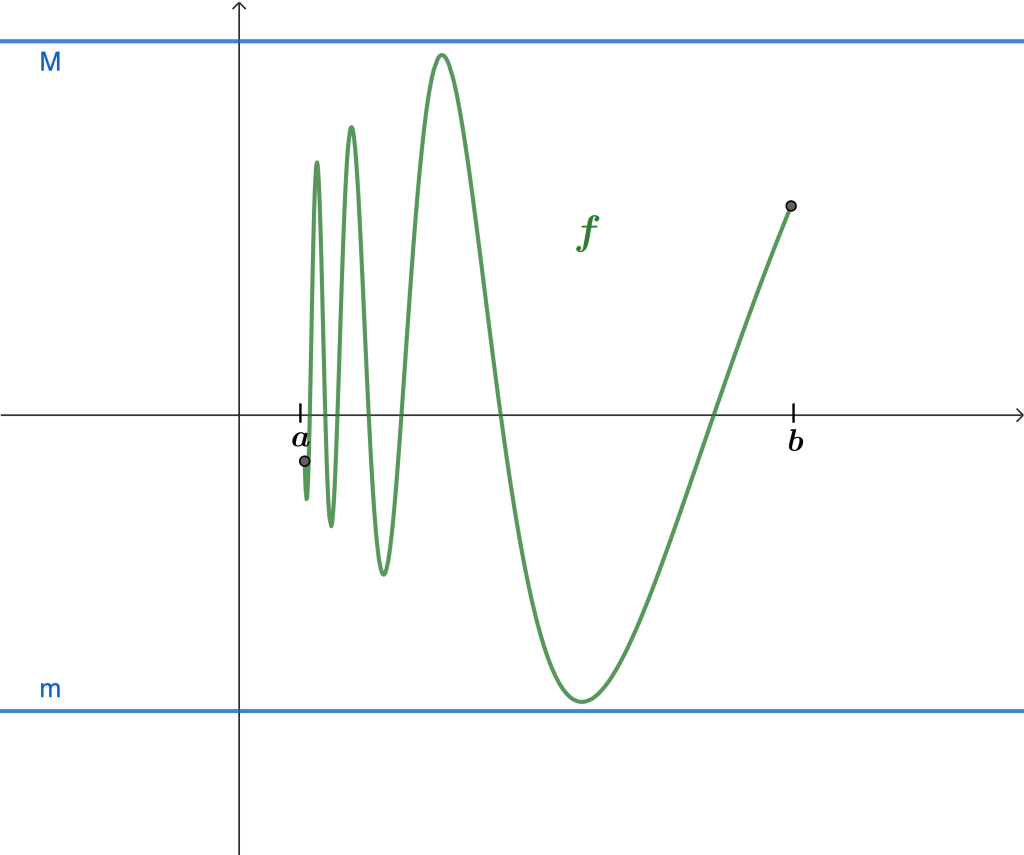
- $f$ está acotada $\Leftrightarrow$ existe $m, M \in \r$ tal que $m \leq f(x) \leq M$ para todo $x \in A$.
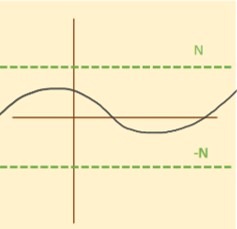
- Una equivalencia para la última definición sería:
$f$ está acotada $\Leftrightarrow$ existe $N \in \r$ tal que $|f(x)| \leq N$ para todo $x \in A$.
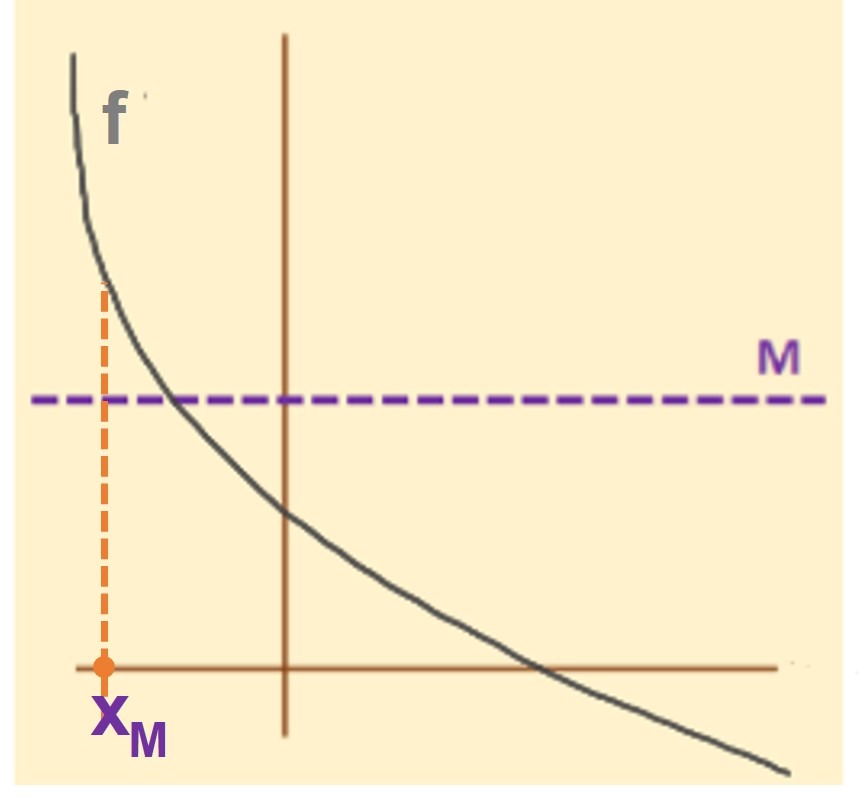
- $f$ no está acotada $\Leftrightarrow$ para toda $M >0$ existe $x_{M} \in A$ tal que $|f(x_{M})|>M$.
Ejemplo 1
Si tenemos la función $f: \r^{+} \rightarrow \r$ definida como:
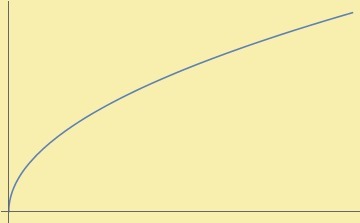
$$f(x)=\sqrt{x}\quad\text{.}$$
Probaremos que $f$ no es acotada en su dominio.
Demostración: Consideremos a $M>0$ y a $x_{M}=(M+1)^{2}$ donde $x_{M} \in D_{f}$. Así al evaluar la función en $x_{M}$ tenemos:
\begin{align*}
f(x_{M})&=f((M+1)^{2})\\
&=\sqrt{(M+1)^{2}}\\
&= M+1
\end{align*}
aquí observamos siempre ocurre que: $M+1>M$
$\therefore f$ es no acotada en su dominio.
$\square$
Ejemplo 2
Ahora si consideramos la función $g: (0, \infty) \rightarrow \r^{+}$ definida como:
\begin{equation*}
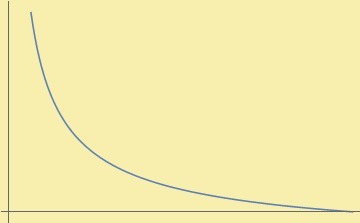
g(x)=\frac{1}{\sqrt[3]{x^{2}}} \quad\text{.}
\end{equation*}
Veremos ahora que $g$ no es acotada en su dominio.
Demostración: Sea $N>0$ y a $x_{N} \in D_{g}$ definida como:
\begin{equation*}
x_{N}= \frac{1}{(N+1)^{\frac{3}{2}}}\quad\text{.}
\end{equation*}
Al tomar $g(x_{N})$ tenemos:
\begin{align*}
g(x_{N})&=g\left(\frac{1}{(N+1)^{\frac{3}{2}}}\right)\\
&=\frac{1}{\left(\frac{1}{(N+1)^{\frac{3}{2}}}\right)^{\frac{2}{3}}}\\
&=\frac{1}{\frac{1}{N+1}}\\
&=N+1
\end{align*}
donde $N+1>N$ por lo que conluimos que $g$ es no acotada en su dominio.
$\square$
Más adelante
En la siguiente entrada, veremos un conjunto de funciones muy particular: las funciones polinomiales. Adicionalmente, revisaremos las funciones racionales. Para ambos tipos de funciones, examinaremos su definición y algunos ejemplos.
Tarea moral
- Dada la función $f(x)=x^{3}$. Demuestra que:
- $f$ es creciente en $[0, \infty)$.
- $f$ es creciente en $(-\infty,0)$.
- Demuestra los puntos 1, 2 y 3 del Teorema:
- $f$ par y creciente en el intervalo $[0, \infty) \Rightarrow f$ es decreciente en $(-\infty, 0)$.
- $f$ par y decreciente en el intervalo $[0, \infty) \Rightarrow f$ es creciente en $(-\infty, 0)$.
- $f$ impar y creciente en el intervalo $[0, \infty) \Rightarrow f$ es creciente en $(-\infty, 0)$.
- Demuestra que la función $h: (0,1) \rightarrow \r$ definida como:
$$h(x)=\frac{1}{x^{3}}$$
no es acotada en su dominio.
Entradas relacionadas
- Ir a: Cálculo Diferencial e Integral I
- Entrada anterior del curso: Cálculo Diferencial e Integral I: Funciones pares e impares.
- Entrada siguiente del curso: Cálculo Diferencial e Integral I: Funciones polinomiales y racionales. Análisis geométrico de funciones.
- Resto de cursos: Cursos
Agradecimientos
Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»