Archivo de la etiqueta: combinación lineal

Álgebra Lineal I: Proyecciones, simetrías y subespacios estables

Por Blanca Radillo

9 respuestas

Introducción

Anteriormente introdujimos el concepto de transformaciones lineales entre dos espacios vectoriales. Vimos diversas propiedades que toda transformación lineal debe satisfacer. Finalmente, se presentaron las definiciones de kernel e imagen. Lo que haremos ahora es hablar de algunos tipos especiales de transformaciones lineales: las proyecciones y las simetrías. Para ello, aprovecharemos lo que ya estudiamos de suma y suma directas de subespacios.

Además, hablaremos del concepto de subespacios estables. Intuitivamente, un subespacio es estable para una transformación lineal si al aplicarla en elementos del subespacio, «no nos salimos del subespacio».

Proyecciones

Hablemos de una clase fundamental de transformaciones lineales: las proyecciones sobre subespacios. Para ellas, se comienza expresando a un espacio vectorial como una suma directa $V=W_1\oplus W_2$. Recuerda que, a grandes rasgos, esto quiere decir que cada vector $v$ de $V$ se puede expresar de manera única como $v=w_1+w_2$, donde $w_1$ está en $W_1$ y $w_2$ está en $W_2$.

Definición. Sea $V$ un espacio vectorial y sean $W_1$ y $W_2$ dos subespacios de $V$ tales que $V=W_1\oplus W_2$. La proyección sobre $W_1$ es la función $\pi_1:V\rightarrow W_1$ definido como: para cada $v\in V$, se tiene que $\pi_1(v)$ es el único vector en $W_1$ tal que $v-\pi_1(v)$ está en $W_2$.

De manera similar podemos definir la proyección sobre $W_2$, llamada $\pi_2:V\rightarrow W_2$.

Hay otra forma de decir esto. Dado que $V=W_1\oplus W_2$, para todo $v\in V$ existen únicos vectores $v_1\in W_1$ y $v_2\in W_2$ tales que $v=v_1+v_2$. Entonces $\pi_1(v)=v_1$ y $\pi_2(v)=v_2$.

Ejemplo. Sea $V=\mathbb{R}^2$, y sean $W_1=\{(a,0): a\in\mathbb{R}\}$ y $W_2=\{(0,b):b\in\mathbb{R}\}$. Sabemos que $W_1$ y $W_2$ son subespacios y que $V=W_1\oplus W_2$. Entonces, si $(a,b)\in V$, se tiene que $\pi_1((a,b))=(a,0)$ y $\pi_2((a,b))=(0,b)$.

$\triangle$

Cuando hablamos de una proyección $\pi$ de un espacio vectorial $V$, sin indicar el subespacio, de manera implícita nos referimos a una función para la cual existe una descomposición $V=W_1\oplus W_2$ tal que $\pi$ es la proyección sobre $W_1$.

Problema. Muestra que la transformación lineal $\pi:M_2(\mathbb{R})\to M_2(\mathbb{R})$ tal que $$\pi\begin{pmatrix} a & b \\ c & d \end{pmatrix} = \begin{pmatrix} a + b & 0 \\ c & 0 \end{pmatrix}$$ es una proyección.

Solución. Para resolver el problema, tenemos que mostrar que se puede escribir $M_2(\mathbb{R})=W_1\oplus W_2$, de modo que $\pi$ sea una proyección sobre $W_1$.

Proponemos $$W_1=\left\{\begin{pmatrix} r & 0 \\ s & 0\end{pmatrix}: r,s, \in \mathbb{R}\right\}$$ y $W_2$ como $$W_2=\left\{\begin{pmatrix} -r & r \\ 0 & s\end{pmatrix}: r,s, \in \mathbb{R}\right\}.$$

Si una matriz está simultánteamente en $W_1$ y $W_2$, es sencillo mostrar que únicamente puede ser la matriz cero, es decir $O_2$. Esto lo puedes verificar por tu cuenta. Además, cualquier matriz en $M_2(\mathbb{R})$ se puede escribir como suma de elementos en $W_1$ y $W_2$ como sigue: $$\begin{pmatrix} a & b \\ c & d \end{pmatrix} = \begin{pmatrix} a +b & 0 \\ c & 0 \end{pmatrix} + \begin{pmatrix} -b & b \\ 0 & d \end{pmatrix}.$$

Justo $\pi$ es la primer matriz. Esto muestra que $\pi$ es una proyección, pues es la proyección sobre $W_1$ en la descomposición $V=W_1\oplus W_2$.

$\square$

Aún no hemos mostrado que las proyecciones son transformaciones lineales. Hacemos esto a continuación.

Proposición. Sean $V$ un espacio vectorial, $W_1$ un subespacio vectorial de $V$ y $\pi:V\to W_1$ una proyección de $V$ sobre $W_1$. Entonces $\pi$ es una transformación lineal.

Demostración. Si $v,v’ \in V$ entonces $v+v’\in V$ y por definición de proyección tenemos que $\pi(v+v’)$ es el único vector en $W_{1}$ tal que:

$$(v+v’)-\pi(v+v’)\in W_{2},$$ por otra parte como $\pi(v)$ es el únco vector en $W_{1}$ tal que $v-\pi(v)\in W_{2}$ y $\pi(v’)$ es el único vector en $W_{1}$ tal que $v’-\pi(v’)\in W_{2}$ entonces $v-\pi(v)+v’-\pi(v’)\in W_{2}$ ya que $W_{2}$ es subespacio de $V$, es decir que $$(v+v’)-(\pi(v)+\pi(v’))\in W_{2}$$ y debido a que $\pi(v)+\pi(v’)\in W_{1}$, entonces tenemos la situación en la que existe un vector $\pi(v)+\pi(v’)\in W_{1}$ tal que $$(v+v’)-(\pi(v)+\pi(v’))\in W_{2},$$ pero $\pi(v+v’)$ es el único vector en $W_{1}$ tal que $(v+v’)-\pi(v+v’)\in W_{2}$, esto implica que $$\pi(v+v’)=\pi(v)+\pi(v’).$$ Así concluimos que $\pi$ abre sumas.

Para comprobar que $\pi$ saca escalares consideremos cualquier $v\in V$ y cualquier $c\in F$, tenemos que $cv\in V$ (pues $V$ es espacio vectorial), por definición de proyección tenemos que $\pi(cv)$ es el único vector en $W_{1}$ tal que $$cv-\pi(cv)\in W_{2},$$ por otra parte $\pi(v)$ es el único vector de $W_{1}$ tal que $v-\pi(v)\in W_{2}$ entonces $c(v-\pi(v))=cv-c\pi(v)\in W_{2}$. Como $c\pi(v)\in W_{1}$ tal que $cv-c\pi(v)\in W_{2}$ entonces $$\pi(cv)=c\pi(v)$$ debido a la unicidad de $\pi(cv)$, por lo que $\pi$ saca escalares. Como $\pi$ abre sumas y saca escalares concluimos que $\pi$ es una transformación lineal.

$\square$

Finalmente, notemos que $\pi(v)=v$ para todo $v\in W_1$ pero $\pi(v)=0$ si $v\in W_2$.

Simetrías

Una segunda clase importante de trasnformaciones lineales son las simetrías.

Definición. Sea una descomposición $V=W_1\oplus W_2$, con $W_1, W_2$ dos subespacios de $V$. Decimos que $s:V\rightarrow V$ es una simetría con respecto a $W_1$ a lo largo de $W_2$ si para todo $v\in V$, escrito como $v=v_1+v_2$ con $v_1\in W_1$ y $v_2 \in W_2$, tenemos que $$s(v)=v_1-v_2.$$

Al igual que con las proyecciones, no es dificil ver que las simetrías son transformaciones lineales.

Proposición. Sea $s:V\rightarrow V$ una simetría con respecto a $W_1$ a lo largo de $W_2$. Entonces, $s$ es una transformación lineal.

Demostración. Sean $v,v’ \in V$. Sean $v_1,v’_1\in W_1$ y $v_2,v’_2 \in W_2$ tales que $v=v_1+v_2$ y $v’=v’_1+v’_2$. Eso implica que $v+v’=(v_1+v’_1)+(v_2+v’_2)$ con $v_1+v’_1 \in W_1$ y $v_2+v’_2 \in W_2$. Entonces
$$s(v)+s(v’)=(v_1-v_2)+(v’_1-v’_2) =(v_1+v’_1)-(v_2+v’_2)= s(v+v’).$$
Ahora sea $a\in F$, entonces $as(v)=a(v_1-v_2)=av_1-av_2=s(av_1+av_2)=s(av)$. Por lo tanto, $s$ es una transformación lineal.

$\square$

Notemos que si $v\in W_1$, entonces $s(v)=v-0=v$, y si $v\in W_2$, entonces $s(v)=0-v=-v$.

Subespacios estables

Observemos que las proyecciones y las simetrías satisfacen que $\pi(W_1)=W_1$ y $s(W_1)=W_1$. Esta es una propiedad muy linda, pero en general, si $T:V\rightarrow V$ es una transformación lineal cualquiera y $W$ un subespacio de $V$, no siempre tenemos que $T(W)=W$, o ni siquiera que $T(W)\subset W$. Es decir, aunque tomemos un vector $w$ en $W$, puede pasar que $T(w)$ ya «esté fuera» de $W$.

Los subespacios $W$ que sí satisfacen esta última propiedad son cruciales en el estudio de este curso, y por ello, merecen un nombre especial.

Definición. Sea $V$ un espacio vectorial y $T:V\rightarrow V$ una transformación lineal. Si $W$ es un subespacio de $V$ tal que $T(W)\subset W$, decimos que $W$ es un subespacio estable bajo $T$.

En otras palabras, $W$ es estable bajo $T$ si para todo $v$ en $W$ se tiene que $T(v)$ también está en $W$. Un ejemplo trivial es la transformación identidad con cualquier subespacio $W$. Otro ejemplo trivial es que $V$ y $\{0\}$ son dos subespacios estables bajo cualquier transformación lineal $T:V\rightarrow V$. Otros ejemplos son los ya mencionados: las proyecciones y las simetrías.

En el siguiente ejemplo encontraremos todos los subespacios estables para una cierta transformación.

Ejemplo. Consideremos el mapeo $T:\mathbb{R}^2\rightarrow \mathbb{R}^2$ con $T(x,y)=(y,-x)$. Claramente $T$ es lineal. Sea $W$ un subespacio estable de $\mathbb{R}^2$ bajo $T$. Supongamos que $W$ no es ni $\mathbb{R}^2$, ni el subespacio trivial $\{ (0,0) \}$.

Veremos que no hay ningún otro subespacio estable. Procedamos por contradicción. Suponiendo que hay otro subespacio estable $W$, su dimensión tendría que ser exactamente $1$. Eso implica que $W$ está generado por un vector no cero, digamos $v=(x,y)$. Es decir, cada $w\in W$ lo podemos escribir como $w=av$ donde $a$ es un escalar. En particular $v\in W$.

Como $W$ es estable bajo $T$, entonces $T(v)\in W$, esto es $T(v)=cv$ para algún $c$. Así,
\begin{align*}
(y,-x)&=T((x,y))\\&=T(v)\\&=cv\\&=c(x,y)\\&=(cx,cy).
\end{align*} Igualando ambos extremos, obtenemos que$y=cx$ y $-x=cy$, lo cual implica que $(c^2+1)x=0$. Como $c$ es real, esto implica $x=0$ y por lo tanto $y=0$. Concluimos que $v=(0,0)$, lo cual es una contradicción.

Esto demuestra que los únicos subespacios estables bajo $T$ son $\mathbb{R}^2$ y $\{(0,0)\}$.

$\square$

El siguiente problema estudia un problema inverso. En ella se encuentran todas las transformaciones lineales que dejan fijas «todas las rectas por el vector $0$».

Problema. Sea $V$ un espacio vectorial y $T:V\rightarrow V$ una transformación lineal tal que, para todo $v\in V$, se tiene que $\text{span}(v)$ es un subespacio estable bajo $T$. Entonces existe un escalar $c\in F$ tal que $T(x)=cx$ para todo $x\in V$.

Demostración. Sea $x\in V$ un vector distinto de $0$. Si $L=\text{span}(x)$, tenemos que $T(L)\subset L$ por hipótesis. En particular $T(x)\in L$ y por lo tanto existe $c_x$ tal que $T(x)=c_x x$. Queremos probar que esa constante realmente no depende de $x$.

Sea $y\in V$. Hay dos opciones: $x,y$ son linealmente independientes o no. Supongamos primero que $x,y$ son linealmente independientes. Entonces $x+y \neq 0$ y la igualdad $T(x+y)=T(x)+T(y)$ puede ser escrita como $c_{x+y} (x+y)=c_x x+c_y y$, esto es equivalente a $(c_{x+y}-c_x)x+(c_{x+y}-c_y) y=0.$ Por independencia lineal, $c_{x+y}-c_x=c_{x+y}-c_y=0$ y por lo tanto. $c_x=c_{x+y}=c_y$.

Ahora si $x,y$ no son linealmente independientes, es porque $y=0$ (en cuyo caso cualquier $c_y$ funciona, en particular $c_x$) o bien porque $y=ax$ para algún escalar $a$ no cero. Entonces la igualdad $T(y)=T(ax)=aT(x)$ puede ser escrita como $c_y y=ac_x x=c_x y$, y esto implica que $c_y=c_x$.

En cualquier caso, hemos mostrado que para todo $y\in V$, se tiene que $c_x=c_y$. Definiendo $c=c_x$, se satisface la afirmación de la proposición.

$\square$

Las imágenes y kernels son estables

Otros ejemplos importantes de subespacios estables son las imágenes y los kernels. Esto únicamente funciona para cuando tenemos una transformación lineal de un espacio vectorial a sí mismo.

Proposición. Sea $T:V\to V$ una transformación lineal. Entonces $\ker(T)$ e $\Ima(T)$ son subespacios estables bajo $T$.

Demostración. En la entrada anterior ya vimos que $\ker(T)$ e $\Ima(T)$ son subespacios de $V$. Veamos que son estables bajo $T$.

Tomemos $v\in \ker(T)$. Tenemos que mostrar que $T(v)\in \ker(T)$. Pero esto es cierto pues $$T(T(v))=T(0)=0.$$ Así $T(\ker(T))\subset \ker(T)$ y por lo tanto $\ker(T)$ es estable bajo $T$.

Ahora tomemos $v\in \Ima(T)$. De manera inmediata, $T(v)\in \Ima(T)$. Así, $\Ima(T)$ es estable bajo $T$.

$\square$

Más adelante…

Las proyecciones y simetrías son dos ejemplos de transformaciones lineales que tienen propiedades específicas. Más adelante, cuando hablemos de geometría de espacios vectoriales y del proceso de Gram-Schmidt, veremos que las proyecciones satisfacen propiedades interesantes en términos de ciertas distancias.

La teoría de subespacios estables es muy útil a la hora de construir bases de subespacios vectoriales de manera inductiva. De hecho, los resultados en esta dirección son uno de los ingredientes que usaremos en la demostración del teorema estelar del curso: el teorema espectral.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  • Sea $Y$ es el subespacio $Y=\{(0,r,0): r\in \mathbb{R}\}$ de $\mathbb{R}^3$. Argumenta por qué la transformación $\pi:\mathbb{R}^3\to Y$ dada por $\pi(x,y,z)=(0,y,0)$ es una proyección sobre $Y$. Para ello tendrás que encontrar un subespacio $W$ de $\mathbb{R}^3$ tal que $\mathbb{R}^3=Y\oplus W$ y con el cual $\pi(x,y,z)$ satisface la definición.
  • Sea $X$ el subespacio $X=\{(r,0,0): r\in \mathbb{R} \}$. ¿Es posible ver a la transformación $T:\mathbb{R}^3 \to X$ dada por $T(x,y,z)=(x+y+z,0,0)$ como una proyección sobre $X$? Si tu respuesta es sí, tendrás que dar un espacio $W$ bajo el cual se satisfaga la definición. Si tu respuesta es no, tendrás que mostrar que ningún subespacio $W$ funciona.
  • En el ejemplo de la sección de subespacios estables, ¿qué sucede si trabajamos en $\mathbb{C}^2$ en vez de en $\mathbb{R}^2$? ¿Quienes serían todos los subespacios estables?
  • Sea $B=\{v_1,v_2,\ldots,v_n\}$ una base para un espacio vectorial $V$ sobre un campo $F$. Sea $V_i$ el espacio vectorial generado por $v_i$, es decir, el conjunto de vectores de la forma $cv_i$ con $c\in F$. Como $B$ es base, cada vector $v\in V$ puede escribirse de la forma $$a_1v_1+a_2v_2+\ldots+a_nv_n$$ de manera única. Muestra que para toda $i\in\{1,2,\ldots,n\}$ la función $\pi_i(v)=a_iv_i$ es una proyección sobre $V_i$.
  • Para cada entero $n$, muestra que $\mathbb{R}_n[x]$ es un subespacio de $\mathbb{R}[x]$ que es estable bajo la transformación lineal $T$ que manda a cada polinomio $p(x)$ a su derivada $T(p(x))=p'(x)$.

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104721 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM»

Seminario de Resolución de Problemas: Introducción a principio de inducción

Por Leonardo Ignacio Martínez Sandoval

Deja un comentario

Introducción

El principio de inducción es una de las piedras angulares de las matemáticas y de la resolución de problemas. Es altamente probable que ya lo hayas utilizado previamente, en cursos como Álgebra Superior I y II, en Álgebra Lineal, en Cálculo y varios otros.

En esta entrada y las siguientes repasaremos la idea general del principio de inducción, pero además veremos lo flexible que puede ser en la resolución de problemas.

La idea general que debes tener cuando hagas inducción es pensar en Tlaloc (dios de la lluvia). Imagina que Tlaloc decide que llueva hoy, y además decide que si llueve un día, entonces lloverá también al día siguiente. Como llueve hoy, entonces lloverá mañana, pero como llueve mañana entonces lloverá pasado mañana. De hecho, ¡va a llover todos los días a partir de hoy!

De manera general, el principio de inducción sirve para cuando se quieren probar afirmaciones «para todo número natural $n$» y en donde para probar la afirmación para un valor $n$ es útil tener la validez de la afirmación para los valores anteriores. Sin embargo, se puede también utilizar para probar afirmaciones «a partir de cierto natural». Enunciamos esta versión a continuación.

Principio de inducción. Sea $P(n)$ una afirmación (o proposición o propiedad) que depende del número natural $n$. Si

  • la afirmación $P(a)$ es cierta y
  • la veracidad de la afirmación $P(n)$ implica la veracidad de la afirmación $P(n+1)$,

entonces la afirmación $P(n)$ es cierta para toda $n \geq a$.

En estos términos, a probar la afirmación para $a$ se le conoce como probar la base de inducción. Suponer la veracidad de $P(n)$ para una $n$ se conoce como suponer la hipótesis inductiva, y a probar la veracidad de $P(n+1)$ se le conoce como hacer el paso inductivo. Así, para hacer una prueba por inducción se tienen que hacer los siguientes pasos:

  • Probar la base de inducción, osea, mostrar que $P(a)$ es válido.
  • Suponer, libremente, la hipótesis inductiva, es decir, suponer que $P(n)$ cierto.
  • A partir de la hipótesis inductiva, y el resto de las hipótesis del problema, hacer el paso inductivo, es decir, demostrar $P(n+1)$.

Es muy importante hacer estos tres pasos. Si no se prueba la base de inducción, es como si Tlaloc no decidiera que lloviera hoy: no hay forma de saber qué pasara. Si no se hace el paso inductivo, es como si Tlaloc no dijera nada de la lluvia de un día a partir del anterior.

La creatividad en el uso de la inducción en la resolución de problemas reside en varios aspectos. A veces:

  • Se requiere ingenio para probar el caso base.
  • Se requiere ingenio para saber exactamente cómo usar la hipótesis inductiva para hacer el paso inductivo.
  • Se requiere crear una afirmación auxiliar $Q(n)$ más fuerte que implique a $P(n)$, tal qué $Q(n)$ sí se pueda probar por inducción, pero $P(n)$ no, de lo cual veremos ejemplos en siguientes entradas.

Problemas con solución

Veamos algunos ejemplos de problemas que se pueden resolver utilizando induccicón. En el primer problema vamos a ser muy explícitos en cómo estamos ejecutando la inducción. Esto te puede ayudar cuando estas haciendo tus primeras pruebas de inducción: te ayudará a ser explícito en demostrar la base, en suponer la hipótesis inductiva y en hacer el paso inductivo.

En algunas otras de las demostraciones, vamos a ser un poco más flexibles con cómo se escribe la demostración. No hay que ser totalmente explícitos en qué parte de demostración por inducción se está haciendo. Esto te puede ayudar para cuando ya estas escribiendo una prueba más larga y la parte inductiva sólo es un pequeño fragmento del argumento.

Problema. Sea $n\geq 1$ un número entero y $a_n>a_{n-1}>\ldots>a_1>0$ números reales. Considera todas las expresiones que puedes hacer de la forma $$e_1a_1+e_2a_2+\ldots+e_na_n$$ donde cada $e_i$ es $1$ o $0$. Demuestra que al pasar por todas las $2^n$ posibilidades para las $e_i$ se forman por lo menos $\binom{n+1}{2}$ números diferentes.

Solución. Vamos a proceder por inducción sobre $n$. Hagamos primero la base de inducción. Como queremos demostrar la afirmación para toda $n\geq 1$, el caso base es $n=1$. Cuando $n=1$, tenemos un sólo número real $a_1>0$ y lo que tenemos que demostrar es que hay al menos $\binom{2}{2}=1$ valor en las expresiones que se pueden formar. Si $e_1=0$ o $1$, obtenemos las expresiones $0$ y $a_1$ respectivamente, que son al menos dos. Esto prueba el caso base.

Ahora supongamos la hipótesis inductiva. Es decir, suponemos libremente que para cierta $n$, cada que tomamos $n$ números reales se cumple la afirmación del problema, es decir, que al pasar por las $2^n$ posibilidades de $e_i$, se obtienen al menos $\binom{n+1}{2}$ expresiones diferentes.

La parte final es hacer el paso inductivo. Es decir, a partir de todas las hipótesis del problema, de la hipótesis inductiva, y de otras ideas, tenemos que probar la afirmación para $n+1$. Así, tomemos $n+1$ números reales $$a_{n+1}>a_n>\ldots>a_1>0.$$ Tenemos que mostrar que usando coeficientes $0$ y $1$ podemos formar al menos $\binom{n+2}{2}$ números distintos.

Una buena idea es aprovechar que ya sabemos que los números
$$a_n>\ldots>a_1>0$$ ya hacen varias expresiones. Podemos aplicar la hipótesis inductiva a estos números, y con ello logramos conseguir al menos $\binom{n+1}{2}$ expresiones diferentes. Notemos que estas expresiones también sirven para cuando tenemos a $a_{n+1}$ y le ponemos coeficiente $e_{n+1}=0$. Lo que tenemos que hacer ahora es conseguir $\binom{n+2}{2}-\binom{n+1}{2}=n+1$ expresiones nuevas.

Consideremos la expresión $S=a_1+a_2+\ldots+a_n$ en la que todos los coeficientes son $1$. Esta es claramente mayor que cualquiera de las otras que ya tenemos. Además, todas las expresiones $S+a_{n+1}$, $S+a_{n+1}-a_1$, $S+a_{n+1}-a_2$, $\ldots$, $S+a_{n+1}-a_n$ son mayores que $S$ (pues $a_{n+1}$ es el más grande de los $a_i$’s), son todas diferentes, y son de la forma deseada (pues cada $a_i$ con $1\leq i \leq n$ está en $S$).

De esta forma, conseguimos $n+1$ expresiones distintas y todas ellas mayores que $S$, así que distintas de todas las dadas por la hipótesis inductiva. Con esto completamos la demostración.

$\square$

La inducción sirve para probar afirmaciones que dependen de un número natural. Sin embargo, no siempre es inmediato de dónde sale este natural. A veces ese natural aparece simplemente como el tamaño de algún conjunto involucrado. A veces hay que hacer una demostración para «todos los polinomios» y entonces podríamos intentar hacer inducción sobre el grado del polinomio. En otro problema puede que se tenga que mostrar algo «para todas las matrices» y entonces tal vez tengamos que demostrarlo por inducción sobre las dimensiones de la matriz.

Problema. Se dibuja una cantidad finita de lineas en el espacio de modo que no haya tres de ellas que pasan por un mismo punto. Estas líneas definen regiones en el plano. Muestra que se pueden colorear estas regiones de blanco o negro de modo que no haya dos regiones del mismo color que tengan un lado en común.

El problema no tiene ningún número natural explícitamente en el enunciado. Sin embargo, se pide demostrar algo para una cantidad finita de cosas, así que basta probar la afirmación para $n$ cosas, para todo entero $n\geq 0$. De esta forma, la variable «cantidad de líneas que tenemos» ya es una variable sobre la cual podemos hacer inducción. Hagamos la demostración así.

Solución. Procedamos por inducción sobre el número de líneas. Si tenemos $0$ líneas, sólo hay una región en el plano. La pintamos de blanco.

Ahora, supongamos que cada que tenemos $n$ líneas, no tres de ellas por un punto, podemos hacer una coloración de su conjunto de regiones $R$ de modo que no haya dos adyacentes del mismo color.

Tomemos cualquier conjunto de $n+1$ líneas. Tomemos una de ellas $L$ e ignorémosla por el momento. Por hipótesis inductiva, podemos hacer una coloración para las $n$ líneas que quedan. Al regresar $L$ se hacen nuevas regiones. A las regiones que quedan de un lado de $L$, las dejamos del color que ya tenían. A las que están del otro lado de $L$, les intercambiamos el color (blanco a negro y viceversa).

El nuevo acomodo funciona pues todas las regiones de $R$ totalmente contenidas en alguno de los lados de $L$ siguen sin problemas. Y aquellas regiones de $R$ cortadas por $L$ sólo pueden tener problemas con un lado que caiga sobre $L$. Pero de estos problemas tampoco hay pues de un lado quedaron de un color, y del otro del otro.

$\square$

Observa que en el problema anterior ya no estamos haciendo los pasos de la inducción tan «explícitos».

A veces hay problemas en los que hay una variable entera, pero no necesariamente hay que aplicar inducción para esa variable, sino para otro parámetro que introduzcamos.

Problema. Dado un entero positivo $n$ y un real $x\geq 0$, muestra que $$\floor{x}+\floor{x+\frac{1}{n}}+\floor{x+\frac{2}{n}}+\cdots+\floor{x+\frac{n-1}{n}}=\floor{nx}.$$

Recuerda que $\floor{y}$ es el mayor entero que sea menor o igual a $y$.

Solución. El problema con hacer inducción en $n$ es que no hay una forma sencilla de relacionar el resultado para $n$ y el resultado para $n+1$. Tampoco podemos hacer «inducción sobre $x$» porque $x$ es un número real.

El truco para el problema es probar el resultado para todas las $x$ en el intervalo $[\frac{k}{n},\frac{k+1}{n})$ para todo entero $k\geq 0$. Con esos intervalos cubrimos a todos los reales positivos, y por lo tanto cubrimos todas las posibilidades para $x$. Para probar que se vale en esos intervalos, vamos a proceder por inducción sobre $k$.

Si $k=0$, entonces queremos mostrar el resultado para el intervalo $[0,\frac{1}{n})$. Para las $x$ en este intervalo, cada uno de los términos $x+\frac{i}{n}$ (para $i-0,1,\ldots,n-1$) es menor que $1$ y por lo tanto el lado izquierdo de la igualdad que queremos mostrar tiene puros sumandos $0$ y entonces es igual a $0$. También para las $x$ en este intervalo tenemos $nx<1$, y así el lado derecho también es $0$. Esto prueba la base inductiva.

Supongamos ahora que el resultado es cierto para $x$ en el intervalo $[\frac{k-1}{n},\frac{k}{n})$ para cierto entero $k$. Esto quiere decir que

$$\floor{x}+\floor{x+\frac{1}{n}}+\floor{x+\frac{2}{n}}+\cdots+\floor{x+\frac{n-1}{n}}=\floor{nx}.$$

Tomemos ahora un entero $y$ en el intervalo $[\frac{k}{n},\frac{k+1}{n})$. Notemos que $x=y-\frac{1}{n}$ está en el intervalo anterior, de modo que cumple la igualdad de la hipótesis inductiva. Notemos además que si en

$$\floor{y}+\floor{y+\frac{1}{n}}+\floor{y+\frac{2}{n}}+\cdots+\floor{y+\frac{n-1}{n}}$$

substituimos $y=x+\frac{1}{n}$, obtenemos

$$\floor{x+\frac{1}{n}}+\floor{x+\frac{2}{n}}+\floor{x+\frac{3}{n}}+\cdots+\floor{x+\frac{n}{n}}.$$

El último sumando es $\floor{x+1}=\floor{x}+1$, de modo que en el lado izquierdo tenemos todos los sumandos del lado izquierdo de la hipótesis inductiva y un $1$. Así, el lado izquierdo es igual a $$\floor{nx}+1=\floor{nx+1}=\floor{ny},$$ como queríamos mostrar.

$\square$

Más ejemplos

Puedes encontrar más ejemplos en la Sección 2.1 del Problem Solving through Problems de Loren Larson. Otro libro con muchos ejemplos interesantes es el Putnam and Beyond, de Gelca y Andreescu. Así mismo, aquí en el blog hay otras entradas en las que se hacen pruebas por inducción.

El lema de intercambio de Steinitz

Por Leonardo Ignacio Martínez Sandoval

7 respuestas

Introducción

En esta entrada platicaré de un lema muy útil en álgebra lineal, sobre todo cuando se están definiendo las nociones de base y de dimensión para espacios vectoriales de dimensión finita. Se trata del lema de intercambio de Steinitz.

Supondré que el lector ya sabe un poco de álgebra lineal, pero muy poquito. Basta con saber la definición de espacio vectorial. Lo demás lo definiremos sobre el camino.

El nombre del lema es en honor al matemático alemán Ernst Steinitz. Sin embargo, personalmente a mi me gusta pensarlo como el lema del «regalo de vectores», por razones que ahorita platicaremos. El enunciado es el siguiente:

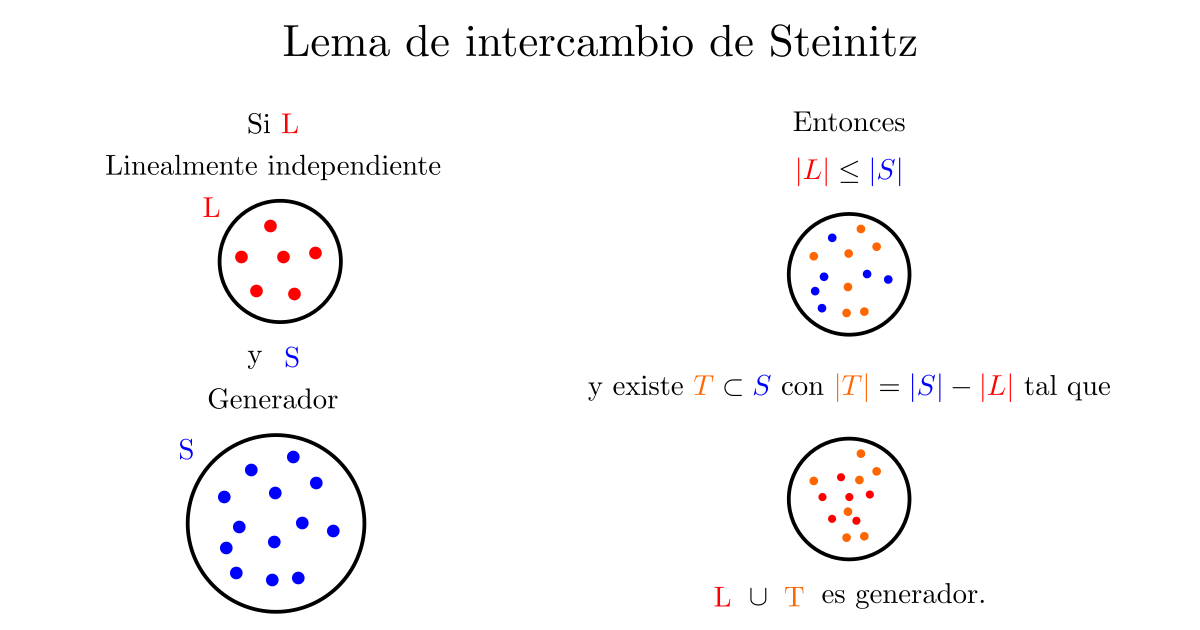
Teorema (Lema de intercambio de Steinitz). Sea $V$ un espacio vectorial. Tomemos un conjunto finito y linealmente independiente $L$ de $V$, y un conjunto finito y generador $S$ de $V$. Supongamos que $L$ tiene $m$ elementos y que $S$ tiene $n$ elementos. Entonces:

  • $m\leq n$
  • Se puede tomar un subconjunto $T$ de $S$ de tamaño $n-m$ tal que $L\cup T$ sea generador de $V$.

En pocas palabras, «cualquier conjunto linealmente independiente tiene a lo mucho tantos elementos como cualquier conjunto generador y, además, cualquier generador le puede regalar vectores al linealmente independiente para volverlo generador».

De manera esquemática, está pasando lo siguiente:

Diagrama del lema de intercambio de Steinitz
Diagrama del lema de intercambio de Steinitz

Lo que haremos es hablar de las definiciones necesarias para entender el lema, hablar de la intuición detrás, dar un par de ejemplos y luego dar la demostración. La presentación está ligeramente basada en el libro de álgebra lineal de Titu Andreescu.

Definiciones e intuición

Sea $V$ un espacio vectorial sobre un campo $F$.

Si tenemos vectores $v_1,\ldots,v_n$ de $V$ y escalares $a_1,\ldots,a_n$ en $F$, podemos considerar al vector formado por multiplicar los vectores por los escalares correspondientes y sumarlos todos, es decir al vector $v$ dado por la expresión $a_1v_1+\cdots+a_nv_n$ . En este caso, decimos que $v$ es una combinación lineal de $v_1,\ldots,v_n$, o a veces que $v_1,\ldots,v_n$ generan a $v$.

Un conjunto $S=\{v_1,v_2,\ldots,v_n\}$ de vectores de $V$ es generador si para cualquier $v$ de $V$ existen escalares $a_1,\ldots,a_n$ en $F$ para los cuales $v=a_1v_1+\cdots+a_nv_n$. Dicho de otra forma, «$S$ es generador si cualquier vector del espacio vectorial es combinación lineal de vectores de $S$».

De esta definición es fácil ver que si $S$ es un conjunto generador y $T$ es un conjunto que contiene a $S$ (es decir, $T\supset S$), entonces $T$ también es generador: simplemente para cualquier $v$ usamos la combinación lineal que tenemos en $S$ y al resto de los vectores (los de $T\setminus S$) les ponemos coeficientes cero.

Un conjunto $L=\{w_1,w_2,\ldots,w_m\}$ de vectores de $V$ es linealmente independiente si la única combinación lineal de vectores de $L$ que da $0$ es aquella en la que todos los escalares son $0$. Dicho de otra forma, «$L$ es linealmente independiente si $a_1w_1+\ldots+a_mw_m=0$ implica que $a_1=a_2=\ldots=a_m=0$.»

Con los conjuntos linealmente independientes pasa lo contrario a lo de los generadores. Si $L$ es un conjunto linealmente independiente y $M$ está contenido en $L$ (es decir, ahora $M\subset L$), entonces $M$ es linealmente independiente. Esto sucede pues cualquier combinación lineal de $M$ también es una combinación lineal de $L$. Como no hay ninguna combinación lineal no trivial de elementos de $L$ que sea igual a cero, entonces tampoco la hay para $M$.

Los párrafos anteriores dejan la idea de que «los conjuntos generadores tienen que ser grandes» y que «los conjuntos linealmente independientes tienen que ser chiquitos». El lema de intercambio de Steinitz es una manera en la que podemos formalizar esta intuición.

Como los conjuntos generadores son «grandes», entonces son bien buena onda y bien generosos. Tienen muchos elementos. Como los conjuntos linealmente independientes son «chiquitos», entonces necesitan elementos. Lo que dice el lema de intercambio de Steinitz es que si tenemos a un generador $S$ y a un linealmente independiente $L$, entonces $S$ tiene más elementos y que puede regalar al linealmente independiente $L$ algunos elementos $T$ para que ahora $L\cup T$ tenga tantos elementos como tenía $S$ y además se vuelva generador. Una cosa importante es que no cualquier subconjunto $T$ funciona. Este tiene que estar bien elegido.

Ejemplo concreto del lema de intercamio de Steinitz

Veamos un ejemplo muy concreto. Supongamos que nuestro espacio vectorial es $\mathbb{R}^3$, osea, los vectores con $3$ entradas reales. Tomemos a los siguientes conjuntos de vectores:

  • $L=\{(1,2,3), (0,3,0)\}$
  • $S=\{(0,1,0), (1,0,0), (0,0,-1), (2,4,6)\}$

Por un lado, el conjunto $L$ es linealmente idependiente. Una combinación lineal $a(1,2,3)+b(0,3,0)=(0,0,0)$ implica de manera directa que $a=0$ (por la primer o tercer coordenadas) y de ahí $b=0$ (por la segunda coordenada).

Por otro lado, el conjunto $S$ es generador, pues con $(0,0,-1)$ podemos obtener a $(0,0,1)$ como combinación lineal, de modo que $S$ genera a los tres de la base canónica y por tanto genera a todo $\mathbb{R}^3$.

Notemos que en efecto $L$ tiene menos elementos que $S$. Además, el lema de intercambio de Steinitz garantiza que $S$ puede pasarle $|S|-|L|=4-2=2$ elementos a $L$ para volverlo generador. Pero hay que ser cuidadosos. Si le regala los elementos $(0,1,0)$ y $(2,4,6)$, entonces no funciona (se puede verificar que este conjunto no genera a $\mathbb{R}^3$). Pero si le regala, por ejemplo, los elementos $(1,0,0)$ y $(0,0,-1)$ entonces ahora sí generará (se puede argumentar viendo que entonces ahora genera a los tres de la base canónica).

Demostración del lema de intercambio de Steinitz

Pasemos ahora a la demostración del lema de Steinitz. Lo demostraremos por inducción en la cantidad de elementos que tiene $L$, el linealmente independiente. Si $|L|=m=0$, entonces claramente $m=0\leq n$, y además $S$ le puede pasar $n-0=n$ elementos (todos) a $L$ y volverlo generador.

Supongamos entonces que es cierta la siguiente afirmación.

Hipótesis inductiva Sea $V$ un espacio vectorial. Tomemos un conjunto finito y linealmente independiente $L$ de $V$, y un conjunto finito y generador $S$ de $V$. Supongamos que $L$ tiene $m$ elementos y que $S$ tiene $n$ elementos. Entonces:

  • $m\leq n$
  • Se puede tomar un subconjunto $T$ de $S$ de tamaño $n-m$ tal que $L\cup T$ sea generador de $V$.

Para el paso inductivo, tomemos $L=\{w_1,w_2,\ldots,w_m,w_{m+1}\}$ un linealmente independiente de $V$ y $S=\{v_1,v_2,\ldots,v_n\}$ un generador de $V$. Aplicándole la hipótesis inductiva al linealmente independiente $L’=L\setminus \{w_{m+1}\}=\{w_1,\ldots,w_m\}$ y al generador $S$, tenemos que:

  • $m\leq n$
  • Se puede tomar un subconjunto $T’=\{s_1,s_2,\ldots,s_{n-m}\}$ de $S$ tal que $L’\cup T’= \{w_1,w_2,\ldots,w_m,s_1,\ldots,s_{n-m}\}$ sea generador de $V$.

Como $L’\cup T’$ es generador, entonces podemos poner a $w_{m+1}$ como combinación lineal de elementos de $L’\cup T’$, es decir, existen $a_1,\ldots, a_m, b_1,\ldots,b_{n-m}$ tales que $$w_{m+1}=a_1w_1+\ldots+a_mw_m+b_1s_1+\ldots+b_{n-m}s_{n-m}.$$

Ya sabemos que $m\leq n$. Si $m=n$, la combinación lineal anterior no tendría ningún $s_i$, y entonces sería una combinación lineal no trivial para los elementos de $L$, lo cual es una contradicción pues $L$ es linealmente independiente. Entonces $m\neq n$ y $m\leq n$, así que $m+1\leq n$, que era el primer punto que queríamos probar.

También, como $L$ es linealmente independiente, no se vale que todos los $b_i$ sean iguales a cero. Sin perder generalidad, podemos suponer que $b_1\neq 0$. Así, $s_1$ se puede despejar como combinación lineal en términos de $w_1,\ldots,w_n,w_{n+1}, s_2,\ldots,s_{n-m}$ y por lo tanto $L\cup (T’\setminus \{s_1\})$ genera lo mismo que $L’\cup T’$, que era todo $V$. Así, $T:=T’\setminus \{s_1\}$ es el subconjunto de $S$ de tamaño $n-(m+1)$ tal que $L\cup T$ es generador. Esto termina la prueba del lema.

Algunas aplicaciones

El lema de intercambio de Steinitz se puede utilizar para probar varias afirmaciones con respecto a bases de un espacio vectorial de dimensión finita.

Un espacio vectorial es de dimensión finita si tiene un conjunto generador con una cantidad finita de elementos. Una base de un espacio vectorial es un conjunto que sea simultáneamente generador y linealmente independiente.

Las siguientes afirmaciones se siguen directamente del lema de Steinitz.

  1. Todas las bases de un espacio vectorial finito tienen la misma cantidad de elementos.
  2. En un espacio vectorial de dimensión $d$:
    • Todo conjunto linealmente independiente tiene a lo más $d$ elementos.
    • Todo conjunto generador tiene al menos $d$ elementos.
  3. Si $S$ es un conjunto con $n$ vectores de un espacio vectorial de dimensión $n$, entonces las siguientes tres afirmaciones son equivalentes:
    • El conjunto $S$ es base.
    • $S$ es linealmente independiente.
    • $S$ es generador.

Como primer ejemplo, haremos (1). Tomemos $B_1$ y $B_2$ bases de un espacio vectorial de dimensión finita $B$. Pensando a $B_1$ como linealmente independiente y a $B_2$ como generador, tenemos $|B_1|\leq |B_2|$. Pensando a $B_2$ como linealmente independiente y a $B_1$ como generador, tenemos $|B_2|\leq |B_1|$. Así, $|B_1|=|B_2|$.

Como segundo ejemplo, haremos una parte de (3). Suponiendo que $S$ es un conjunto de $n$ vectores de un espacio vectorial de dimensión $n$, veremos que su independencia lineal implica $S$ es base. Sea $B$ una base de $V$. Por el lema de Steinitz, podemos pasar $|B|-|S|=n-n=0$ elementos de $B$ a $S$ para volverlo generador. Es decir, $S$ ya es generador. Como además es linealmente independiente, entonces es base.

El resto de las demostraciones son igual de sencillas, como puedes verificar.

Más adelante…

El lema de Steinitz es la herramienta clave para definir dar la definición de dimensión de espacios vectoriales en el caso de dimensión finita. Lo usaremos una y otra vez. Por esta razón, es muy recomendable repasar su demostración y entender a profundidad qué dice.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  • Replica por tu cuenta la demostración del lema de Steinitz hasta que te sientas cómodo con los argumentos.
  • En el ejemplo que se dio de la aplicación del lema de Steinitz, ¿cuáles son todas las posibilidades de $2$ elementos que se pueden pasar para que $L$ se convierta en generador?
  • Usa el lema de Steinitz para demostrar el resto de consecuencias que mencionamos.
  • ¿Qué te dice el lema de Steinitz cuando $L$ y $S$ son inicialmente del mismo tamaño?
  • Muestra que en el lema de Steinitz la hipótesis de que $L$ sea finito no es necesaria, es decir, que incluso sin esta hipótesis se pueden mostrar todas las conclusiones.

Entradas relacionadas

¿Ahora qué?

Si te gustó esta entrada, puedes compartirla o revisar otras relacionadas con matemáticas a nivel universitario:

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104721 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM»

Busca una contradicción

Por Leonardo Ignacio Martínez Sandoval

Deja un comentario

HeuristicasTerminamos esta serie de técnicas de resolución de problemas con una de las técnicas más finas y más usadas en las matemáticas: las pruebas por contradicción.

La idea es la siguiente. Por un momento suponemos que lo que queremos demostrar es falso. Después trabajaremos haciendo todo lo demás correctamente. La idea es llegar a una contradicción con las hipótesis del problema, o bien a algo que sabemos que es imposible. De esta forma, sabemos que debe haber un error en la demostración de eso imposible. Y como lo único que hicimos mal fue suponer que lo original era falso, debemos tener que en realidad es verdadero.

En estos videos veremos varios ejemplos de este argumento para acostumbrarnos. Es súper útil pensar en estos argumentos casi automáticamente.

Ir a los videos…