Introducción
En las entradas anteriores comenzamos a hablar acerca de cómo resolver algunas ecuaciones en $\mathbb{C}$. Platicamos de ecuaciones cuadráticas y la fórmula general. Luego, vimos sistemas de ecuaciones lineales y varios métodos para resolverlos. Lo siguiente que haremos será resolver ecuaciones de la forma $z^n=w$, en donde $w$ en $\mathbb{C}$ y $n$ en $\mathbb{N}$ están dados y $z$ es la variable a determinar. Antes de resolver esta ecuación, necesitamos entender mejor la multiplicación en $\mathbb{C}$, y para ello vamos a estudiar la forma polar de un complejo.
En esta entrada comenzaremos recordando las coordenadas rectangulares de un número complejo, además definiremos sus coordenadas polares. Veremos cómo pasar de coordenadas rectangulares a polares de manera biyectiva, con lo cual podremos definir qué es la forma polar.
Más adelante, la forma polar nos ayudará a entender mejor la geometría de la multiplicación y exponenciación en $\mathbb{C}$. Esto será muy útil cuando queramos «sacar raíces $n$-ésimas», lo cual necesitaremos para resolver ecuaciones del estilo $z^n=w$.
De coordenadas rectangulares a coordenadas polares
Tomemos un número complejo $z=x+yi$ y pensémoslo como un punto del plano complejo, es decir, como el punto $(x,y)$ . Diremos que $(x,y)$ son las coordenadas rectangulares de $z$. Es recomendable recordar la siguiente figura, y regresar a ella frecuentemente.
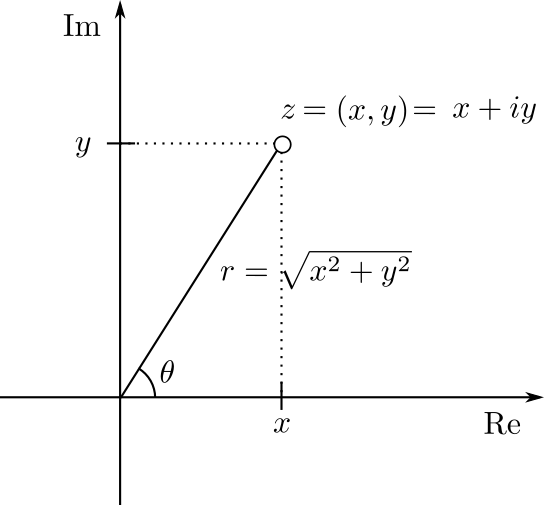
El número complejo $z$ tiene norma $r=\sqrt{x^2+y^2}$. Además, si $z\neq 0$, tenemos que $z$ define un ángulo $\theta$ con el eje real positivo, medido en el sentido contrario al avance de las manecillas del reloj a partir del eje real positivo, al cual le llamaremos el argumento de $z$ y lo denotaremos por $\text{arg}(z)$. Todos los ángulos que manejamos están en radianes.
Sin embargo, este ángulo no es único. El complejo $z$ define al ángulo $\theta$ pero, por ejemplo, también define al ángulo $\theta+2\pi$, pues la suma de $2\pi$ corresponde a dar una vuelta completa alrededor del origen. Por ello, pensaremos que el argumento de $z$ toma todos los valores $$\{\theta+2k\pi:k\in \mathbb{Z}\}.$$ Así, $\text{arg}(z)$ es una multifunción, algo así como una función, pero que toma varios valores. Cuando digamos que un complejo tiene argumento $\theta$, nos referiremos a $\theta$ o cualquier otro ángulo que difiera un múltiplo entero de $2\pi$ Más adelante hablaremos de esto con detalle.
Aunque haya varios ángulos que le correspondan a $z$, hay uno único en el intervalo $[0,2\pi)$.
Definición. Definimos las coordenadas polares de un número complejo $z=x+yi$ como sigue:
- Si $z=0$, sus coordenadas polares son $(0,0)$.
- Si $z\neq 0$, entonces tomamos $r=\Vert z \Vert = \sqrt{x^2+y^2}$ y $\theta$ el único ángulo en $[0,2\pi)$ que hace $z$ con el eje real positivo. Las coordenadas polares de $z$ son $(r,\theta)$.
Observa que $r$ siempre es no negativo y es cero si y sólo si $z=0$. Además por trigonometría para el ángulo $\theta$ se cumple que \begin{align*}\sin \theta &= \frac{y}{r}\\ \cos \theta &= \frac{x}{r},\end{align*} lo cual nos da la siguiente forma práctica para encontrar $\theta$:
- Calculamos $\frac{y}{r}$ o $\frac{x}{r}$ (el que parezca más sencillo).
- Aplicamos una función trigonométrica inversa para reducir el problema a dos opciones.
- Elegimos la opción correcta de acuerdo al signo de $x$ o $y$.
Ejemplo. Tomemos al complejo $z=3-3\sqrt{3}i$. Vamos a pasarlo a forma polar. Su norma es $\sqrt{9+27}=\sqrt{36}=6$. Para determinar el ángulo $\theta$ que define con el eje real, podemos notar que $$\cos{\theta}=\frac{3}{6}=\frac{1}{2},$$ así que $\theta = \frac{\pi}{3}$ ó $\theta= 2\pi-\frac{\pi}{3}=\frac{5\pi}{3}$, pues son los únicos ángulos en $[0,2\pi)$ con ese coseno. Como la parte imaginaria es negativa, se da el segundo caso. Por lo tanto, las coordenadas polares de $z$ son $\left(6,\frac{5\pi}{3}\right)$.
$\triangle$
De coordenadas polares a coordenadas rectangulares
También hay una forma de pasar de coordenadas polares a coordenadas rectangulares. En efecto, tomemos un real no negativo $r$ y consideremos la pregunta ¿quienes son los números complejos de norma $r$?
Por un lado, si $r=0$, necesitamos que $x^2+y^2=0^2=0$, de donde $x=y=0$, así que las coordenadas rectangulares deben ser $(0,0)$. Por otro lado, si $r>0$, se necesita que $$x^2+y^2=r^2,$$ lo cual, por el teorema de Pitágoras, define una circunferencia de radio $r$ con centro en el origen.
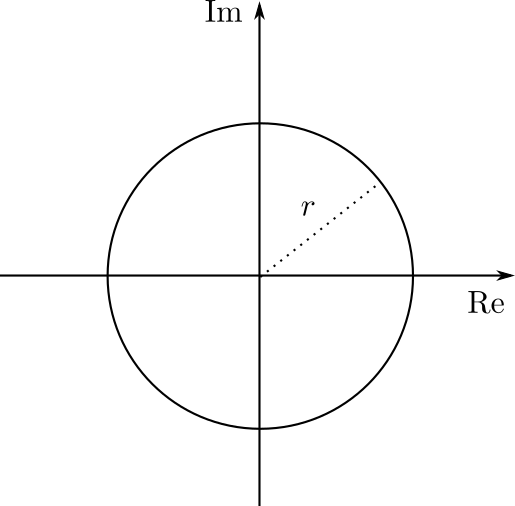
Si además elegimos un ángulo, $\theta$ en $[0,2\pi)$, que el complejo haga con el eje real, entonces queda determinado de manera única. Supongamos que este complejo es $z=x+yi$
Por trigonometría, tenemos que
\begin{align*}x&=r\cos \theta\\ y &= r\sin \theta.\end{align*}
Problema. Determina en la forma $x+yi$ al número complejo cuyas coordenadas polares son $\left(7,\frac{3\pi}{4}\right)$.
Solución. Usamos las fórmulas obtenidas arriba. Tenemos que
\begin{align*}\\
x&=7\cos \frac{3\pi}{4}=7\cdot \left(-\frac{1}{\sqrt{2}}\right)=-\frac{7}{\sqrt{2}}\\
y &= 7\sin \frac{3\pi}{4}= 7\cdot \frac{1}{\sqrt{2}}=\frac{7}{\sqrt{2}}.
\end{align*}
De este modo, el complejo buscado es el $$-\frac{7}{\sqrt{2}}+\frac{7}{\sqrt{2}}.$$
$\square$
Los cambios de coordenadas son inversos entre sí
La primer sección explica cómo de coordenadas rectangulares podemos pasar a coordenadas polares. La anterior dice cómo pasar de coordenadas polares a rectangulares. Resulta que estas operaciones son inversas la una de la otra como veremos en la siguiente:
Proposición. Si tomamos coordenadas polares $(r,\theta)$ de un complejo, las pasamos a coordenadas rectangulares $(x,y)$ y luego éstas las pasamos a coordenadas polares $(r’,\theta’)$ de nuevo, tenemos que $$(r,\theta)=(r’,\theta’).$$
Demostración. En el caso $r=0$, sólo definimos coordenadas polares con $\theta=0$. Al ir a coordenadas rectangulares vamos al punto $(0,0)$, que de nuevo regresa a polares $(0,0)$. Podemos suponer entonces que $r>0$.
Como mencionamos en la segunda sección, las coordenadas rectangulares correspondientes a $(r,\theta)$ son exactamente $$(x,y)=(r\cos \theta,r\sin \theta).$$ Pasemos este complejo a coordenadas polares $(r’,\theta’)$. Usando la identidad pitagórica $\cos ^2\theta + \sin^2 \theta = 1$, la norma de este complejo es
\begin{align*}
\sqrt{r^2\cos^2\theta+r^2\sin^2 \theta} &= r\sqrt{\cos ^2\theta +\sin^2 \theta}\\
&=r\sqrt{1}\\
&=r,
\end{align*}
lo que prueba $r=r’$. Además, como discutimos en la primer sección, tenemos que
\begin{align*}
\sin \theta’ = \frac{r\sin \theta}{r} = \sin \theta\\
\cos \theta’ = \frac{r\cos \theta}{r}=\cos \theta.
\end{align*}
De esta forma, $\theta$ y $\theta’$ son ángulos en $[0,2\pi)$ con el mismo seno y coseno, lo cual implica $\theta=\theta’$.
$\square$
Corolario. El cambio de coordenadas rectangulares a polares , visto como una función de $$\mathbb{R}\times \mathbb{R}$$ a $$(\mathbb{R}^+\times [0,2\pi))\cup \{(0,0)\}$$ es biyectivo.
La forma polar de un número complejo
En las secciones anteriores pensamos a los complejos como parejas ordenadas. Podemos regresar los resultados obtenidos a la forma $x+yi$ de los complejos para justificar la siguiente definición.
Definición. La forma polar de un número complejo $z=x+yi$ es $z=r(\cos \theta + i\sin \theta)$, donde $(r,\theta)$ son las coordenadas polares de $(x,y)$.
Por costumbre, en la forma polar se pone $i$ antes de $\sin \theta$, a diferencia de la forma rectangular, en donde se pone $i$ después de $y$. A veces en expresiones como las de la forma polar aparecen ángulos $\theta$ fuera del rango $[0,2\pi)$. Podemos hacer las cuentas que necesitemos fuera de este rango sin problema. Al final podemos sumar o restar un múltiplo entero de $2\pi$ para caer en el rango $[0,2\pi)$. Esto no cambia el seno ni coseno del ángulo, por lo que no cambia al número complejo.
Como la expresión $ \cos \theta + i\sin \theta$ se usa mucho, usualmente se abrevia.
Definición. Para un ángulo $\theta$ definimos $\text{cis}(\theta) = \cos \theta + i \sin \theta$.
Problema. Determina la forma polar de los complejos $1$, $-1$, $i$ y $-i$.
Solución. Todos estos números tienen norma $1$. Además, hacen ángulos $0, \pi, \frac{\pi}{2}, \frac{3\pi}{2}$ con el eje real positivo, respectivamente. De esta forma, sus coordenadas polares son
\begin{align*}
(1,0)\quad (1,\pi)\quad\left(1,\frac{\pi}{2}\right)\quad \left(1,\frac{3\pi}{2}\right),
\end{align*}
respectivamente.
De esta forma, la forma polar de cada uno es:
\begin{align*}
1&=\cos 0+i \sin 0=\text{cis} (0)\\
-1&=\cos \pi + i \sin \pi = \text{cis} (\pi) \\
i&=\cos \frac{\pi}{2} + i \sin \frac{\pi}{2} = \text{cis} \left(\frac{\pi}{2}\right)\\
-i&= \cos \frac{3\pi}{2} + i \sin \frac{3\pi}{2} = \text{cis} \left( \frac{3\pi}{2}\right).
\end{align*}
$\triangle$
Una aclaración muy importante es que la forma polar de $z=x+yi$ no es $r+\theta i$. La forma polar es exactamente el mismo número complejo que el original, simplemente escrito de manera diferente.
Si la forma polar de un complejo es exactamente el mismo número que el original, ¿de qué nos sirve tenerlo en coordenadas polares? Resulta que la multiplicación compleja se entiende mucho mejor en términos de la forma polar. En la siguiente entrada veremos esto y cómo lo podemos usar para encontrar potencias de números complejos fácilmente.
Más adelante…
Tarea moral
A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.
- Determina la forma polar de los siguientes complejos: $7-7i$ y $-2+2\sqrt{3}i$.
- Determina la forma rectangular de los complejos con coordenadas polares $\left(2,\frac{\pi}{3}\right)$ y $\left(1, \frac{11\pi}{6}\right)$.
- Si la forma polar del complejo $z$ es $r\text{cis} \theta$, ¿quién es la forma polar del conjugado?
- ¿Cuáles son aquellos números complejos que se obtienen al variar $\theta$ en la forma polar $3\text{cis}(\theta)$?
- ¿Qué figura en el plano definen aquellos números complejos que se obtienen al variar $r$ en la forma polar $r\text{cis}(\pi)$?
Puedes practicar más estos temas viendo los videos y haciendo los ejercicios de la página de Khan Academy, de su sección de números complejos.
Entradas relacionadas
- Ir a: Álgebra Superior II
- Entrada anterior del curso: Sistemas de ecuaciones lineales complejos
- Entrada siguiente del curso: Problemas de sistemas de ecuaciones complejos y forma polar
Agradecimientos
Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»
