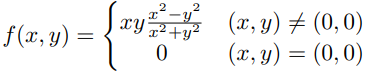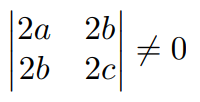Diferenciabilidad de Funciones de $\mathbb{R}^{2}\rightarrow \mathbb{R}$
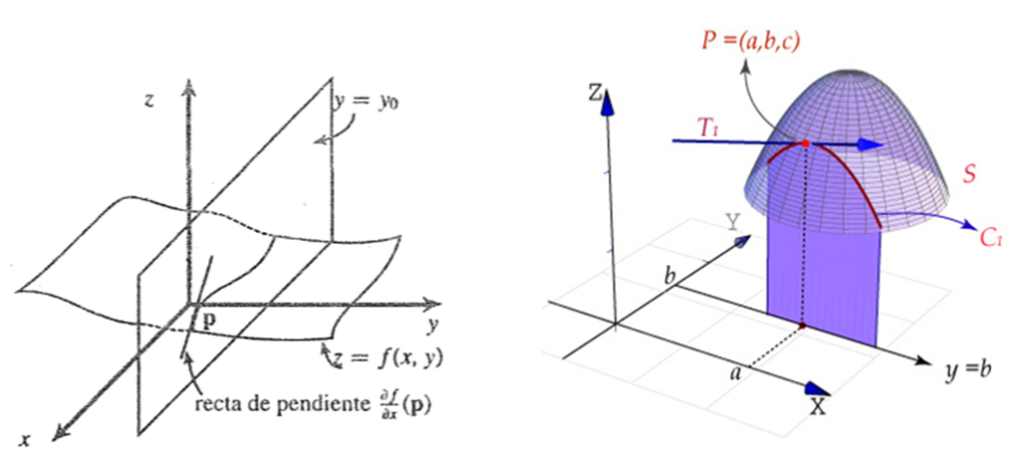
Definición. Sea $A\subset\mathbb{R}^{2}$, un abierto, $f:A\rightarrow\mathbb{R}$ y $(x_{0},y_{0})\in A$. Se dice que f es diferenciable en $(x_{0},y_{0})$ si existen las derivadas parciales $\displaystyle{\frac{\partial f}{\partial x}(x_{0},y_{0}),~~\frac{\partial f}{\partial y}}(x_{0},y_{0})$ tal que
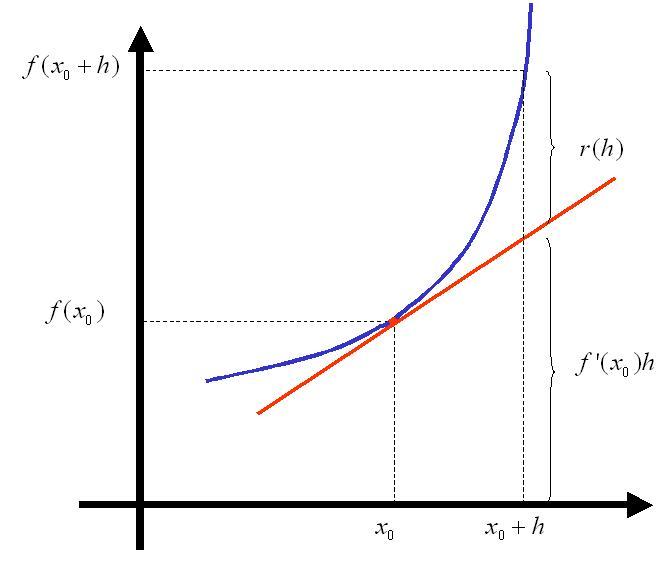
$$f((x_{0},y_{0})+(h_{1},h_{2}))=f(x_{0},y_{0})+\frac{\partial f}{\partial x}(x_{0},y_{0})h_{1}+\frac{\partial f}{\partial y}(x_{0},y_{0})h_{2}+r(h_{1},h_{2})$$donde
$$\lim_{(h_{1},h_{2})\rightarrow(0,0)}\frac{r(h_{1},h_{2})}{|(h_{1},h_{2})|}=0$$
Diferenciabilidad implica continuidad de Funciones de $\mathbb{R}^{2}\rightarrow \mathbb{R}$
Teorema 1. Si la función $f:A\subset\mathbb{R}^{2}\rightarrow \mathbb{R}$ definida en $A$ de $\mathbb{R}^{2}$, es diferenciable en el ´punto $p=(x_{0},y_{0})\in A$, entonces es continua en ese punto.
Demostración. Si f es diferenciable en el ´punto $p=(x_{0},y_{0})\in A$ se tiene
$$f((x_{0},y_{0})+(h_{1},h_{2}))=f(x_{0},y_{0})+\frac{\partial f}{\partial x}(x_{0},y_{0})h_{1}+\frac{\partial f}{\partial y}(x_{0},y_{0})h_{2}+r(h_{1},h_{2})$$
tomando limite se tiene
$$\lim_{(h_{1},h_{2})\rightarrow(0,0)}f((x_{0},y_{0})+(h_{1},h_{2}))=\lim_{(h_{1},h_{2})\rightarrow(0,0)}f(x_{0},y_{0})+\cancel{\frac{\partial f}{\partial x}(x_{0},y_{0})h_{1}}+\cancel{\frac{\partial f}{\partial y}(x_{0},y_{0})h_{2}}+\cancel{r(h_{1},h_{2})}$$
se tiene entonces que
$$\lim_{(h_{1},h_{2})\rightarrow(0,0)}f((x_{0},y_{0})+(h_{1},h_{2}))=f(x_{0},y_{0})$$
por lo que f es continua en $(x_{0},y_{0})$
Aplicacion del Teorema del Valor Medio de Funciones de $\mathbb{R}^{2}\rightarrow \mathbb{R}$}
Teorema 2. Suponga que $f:A\subset\mathbb{R}^{2}\rightarrow\mathbb{R}$ es tal que
$$\left|\frac{\partial f}{\partial x}(x_{0},y_{0})\right|\leq M$$ y $$\left|\frac{\partial f}{\partial x}(x_{0},y_{0})\right|\leq M$$
donde $M$ no depende de $x,y$ entonces $f$ es continua en $A$.
Demostración. Sean $(x_{0},y_{0}),(x_{0}+h_{1},y_{0}+h_{2})\in A$ tenemos entonces que $$f(x_{0}+h_{1},y_{0}+h_{2})-f(x_{0},y_{0})=f(x_{0}+h_{1},y_{0}+h_{2})\textcolor{Red}{-f(x_{0}+h_{1},y_{0})+f(x_{0}+h_{1},y_{0})}-f(x_{0},y_{0})$$ Aplicando teorema del valor medio se tiene que existen $\xi_{1},\in\ (x_{0},x_{0}+h_{1})$,$\xi_{2}\in(y_{0},y_{0}+h_{2})$ tal que $$f(x_{0}+h_{1},y_{0}+h_{2})\textcolor{Red}{-f(x_{0}+h_{1},y_{0})}=\frac{\partial f}{\partial y}(x_{0}+h_{1},\xi_{2})h_{2}$$ $$\textcolor{Red}{f(x_{0}+h_{1},y_{0})}-f(x_{0},y_{0})=\frac{\partial f}{\partial x}(\xi_{1},y_{0}+h_{2})h_{1}$$ por lo tanto $$\left|f(x_{0}+h_{1},y_{0}+h_{2})-f(x_{0},y_{0})\right|=\left|\left(\frac{\partial f}{\partial y}(x_{0}+h_{1},\xi_{2})h_{2}\right)+\left(\frac{\partial f}{\partial x}(\xi_{1},y_{0}+h_{2})h_{1}\right)\right|\leq $$ $$\left|\left(\frac{\partial f}{\partial y}(x_{0}+h_{1},\xi_{2})\right)\right||h_{2}|+\left|\left(\frac{\partial f}{\partial x}(\xi_{1},y_{0}+h_{2}\right)\right|)|h_{1}|\leq M(|h_{2}|+|h_{1}|)$$ si tenemos que $\displaystyle{|(h_{1},h_{2})|}<\delta$ entonces $$M(|h_{2}|+|h_{1}|)<2M\delta~\therefore~~~\epsilon=2M\delta\Rightarrow \delta=\frac{\epsilon}{2M}$$
Diferenciabilidad y Derivadas Direccionales
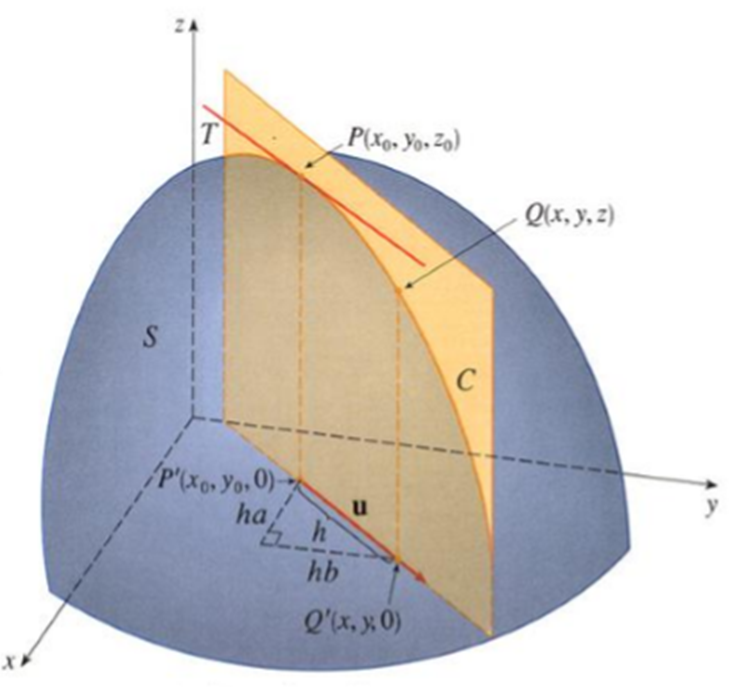
Teorema 3. Si $f:\mathbb{R}^{n}\rightarrow \mathbb{R}$ es una función diferenciable en $x_{0}$ en la dirección del vector unitario u entonces
$$\frac{\partial f}{\partial u}(x_{0})=\sum_{i=1}^{n}\frac{\partial~f}{\partial x_{i}}\cdot u_{i}$$
Demostración. Sea $u\in\mathbb{R}^{n}$ tal que $u\neq0$ y $|u|=1$ como $f$ es diferenciable en $x_{0}$, se tiene que
$$f(x_{0}+h)-f(x_{0})=\sum_{i=1}^{n}\frac{\partial f}{\partial x_{i}}(x_{0})h_{i}+r(h)$$satisface
$$\lim_{(h)\rightarrow 0}\frac{r(h)}{|(h)|}=0$$
tomando $h=tu$ se tiene $|h|=|tu|=|t||u|=|t|$\
se tiene entonces
$$f(x_{0}+t(u))-f(x_{0})=\sum_{i=1}^{n}\frac{\partial f}{\partial x_{i}}(x_{0})tu_{i}+r(tu)$$
tenemos entonces
$$\lim_{t\rightarrow0}\frac{f(x_{0}+t(u))-f(x_{0})}{t}=\sum_{i=1}^{n}\frac{\partial f}{\partial x_{i}}(x_{0})u_{i}+\cancel{\lim_{t\rightarrow0}r(tu)}$$
es decir
$$\frac{\partial f}{\partial u}(x_{0})=\sum_{i=1}^{n}\frac{\partial f}{\partial x_{i}}(x_{0})u_{i}$$ $\square$
Ejemplo. Halle la derivada direccional de $f(x,y)=\ln(x^{2}+y^{3})$ en el punto $(1,-3)$ en la dirección $(2,-3)$
Solución. En este caso
$$u=(2,-3)~\Rightarrow~|u|=\sqrt{13}~\rightarrow~\frac{u}{|u|}=\left(\frac{2}{\sqrt{13}},\frac{-3}{\sqrt{13}}\right)$$
$$\frac{\partial f}{\partial x}(1,-3)=\frac{2x}{x^{2}+y^{3}}\left|_{(1,-3)}\right.=\frac{-2}{26}$$
$$\frac{\partial f}{\partial y}(1,-3)=\frac{3y^{2}}{x^{2}+y^{3}}\left|_{(1,-3)}\right.=\frac{-27}{26}$$
por lo tanto
$$D_{\left(\frac{2}{\sqrt{13}},\frac{-3}{\sqrt{13}}\right)}f\left(1,-3\right)=\left(\frac{-2}{26}\right)\cdot\left(\frac{2}{\sqrt{13}}\right)+\left(\frac{-27}{26}\right)\cdot \left(\frac{-3}{\sqrt{13}}\right)=\frac{77\sqrt{13}}{338}$$
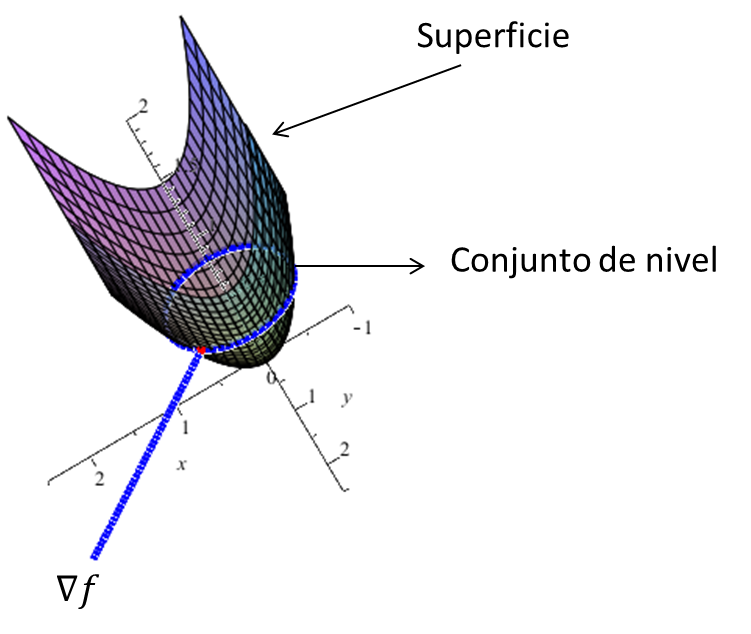
El Gradiente
Sea $f:A\subset \mathbb{R}^{n}\rightarrow \mathbb{R}$ una función diferenciable en $x_{0}\in A$. Entonces el vector cuyas componentes
son las derivadas parciales de f en $x_{0}$ se le denomina Vector Gradiente
$$\left(\frac{\partial f}{\partial x_{1}}(x_{0}),\frac{\partial f}{\partial x_{2}}(x_{0}),…,\frac{\partial f}{\partial x_{n}}(x_{0}),\right)$$
y se le denota por $\nabla f$.
En el caso particular $n=2$ se tiene
$$\nabla f(x_{0})=\left(\frac{\partial f}{\partial x}(x_{0}),\frac{\partial f}{\partial y}(x_{0})\right)$$
En el caso particular $n=3$ se tiene
$$\nabla f(x_{0})=\left(\frac{\partial f}{\partial x}(x_{0}),\frac{\partial f}{\partial y}(x_{0}),\frac{\partial f}{\partial z}(x_{0})\right)$$
Ejemplo. Calcular $\nabla f$ para $f(x,y)=x^{2}y+y^{3}$
Solución. En este caso
$$\nabla f(x,y)=\left(2xy,x^{2}+3y^{2}\right)$$
Teorema 4. Si $f:\mathbb{R}^{2}\rightarrow \mathbb{R}$ es una función diferenciable en $(x_{0},y_{0})$ en la dirección del vector unitario u entonces
$$\frac{\partial f}{\partial u}(x_{0},y_{0})=\nabla f(x_{0},y_{0})\cdot u$$
Sea $u\in\mathbb{R}^{n}$ tal que $u\neq0$ y $|u|=1$ como $f$ es diferenciable en
$(x_{0},y_{0})$, se tiene que
$$f((x_{0},y_{0})+(h_{1},h_{2}))=f(x_{0},y_{0})+\frac{\partial f}{\partial x}(x_{0},y_{0})h_{1}+\frac{\partial f}{\partial y}(x_{0},y_{0})h_{2}+r(h_{1},h_{2})$$
satisface
$$\lim_{(h_{1},h_{2})\rightarrow(0,0)}\frac{r(h_{1},h_{2})}{|(h_{1},h_{2})|}=0$$
tomando $h=tu$ se tiene $|h|=|(h_{1},h_{2})|=|tu|=|t||u|=|t|$
se tiene entonces
$$f((x_{0},y_{0})+t(u))=f(x_{0},y_{0})+\frac{\partial f}{\partial x}(x_{0},y_{0})tu_{1}+\frac{\partial f}{\partial y}(x_{0},y_{0})tu_{2}+r(tu_{1},ru_{2})$$
y también
$$\frac{r(h_{1},h_{2})}{|(h_{1},h_{2})|}=\frac{r(tu_{1},ru_{2})}{|tu|}=\frac{r(tu_{1},ru_{2})}{|t||u|}=\frac{r(tu_{1},ru_{2})}{|t|}$$
tenemos entonces
$$\lim_{t\rightarrow0}\frac{r(tu_{1},ru_{2})}{|t|}=\lim_{t\rightarrow0}\frac{f((x_{0},y_{0})+t(u))-f(x_{0},y_{0})}{|t|}-\frac{\frac{\partial f}{\partial x}(x_{0},y_{0})tu_{1}}{|t|}-\frac{\frac{\partial f}{\partial y}(x_{0},y_{0})tu_{2}}{|t|}$$
es decir
$$0=\frac{\partial f}{\partial u}(x_{0},y_{0})-\frac{\partial f}{\partial x}(x_{0},y_{0})u_{1}-\frac{\partial f}{\partial y}(x_{0},y_{0})u_{2}$$
y en consecuencia
$$\frac{\partial f}{\partial u}(x_{0},y_{0})=\frac{\partial f}{\partial x}(x_{0},y_{0})u_{1}+\frac{\partial f}{\partial y}(x_{0},y_{0})u_{2}=\left(\frac{\partial f}{\partial x}(x_{0},y_{0},\frac{\partial f}{\partial y}(x_{0},y_{0}\right)\cdot\left(u_{1},u_{2}\right)=\nabla f(x_{0},y_{0})\cdot u$$ $\square$
Ejemplo. Halle la derivada direccional de $f(x,y)=\ln(x^{2}+y^{3})$ en el punto $(1,-3)$ en la dirección $(2,-3)$
Solución. En este caso
$$\frac{\partial f}{\partial x}(1,-3)=\frac{2x}{x^{2}+y^{3}}\left|_{(1,-3)}\right.=\frac{-2}{26}$$
$$\frac{\partial f}{\partial y}(1,-3)=\frac{3y^{2}}{x^{2}+y^{3}}\left|_{(1,-3)}\right.=\frac{-27}{26}$$
por lo tanto
$$\nabla f(1,-3)=\left(\frac{-2}{26},\frac{-27}{26}\right)\cdot \left(\frac{2}{\sqrt{13}},\frac{-3}{\sqrt{13}}\right)=\frac{77}{26\sqrt{13}}=\frac{77\sqrt{13}}{338}$$
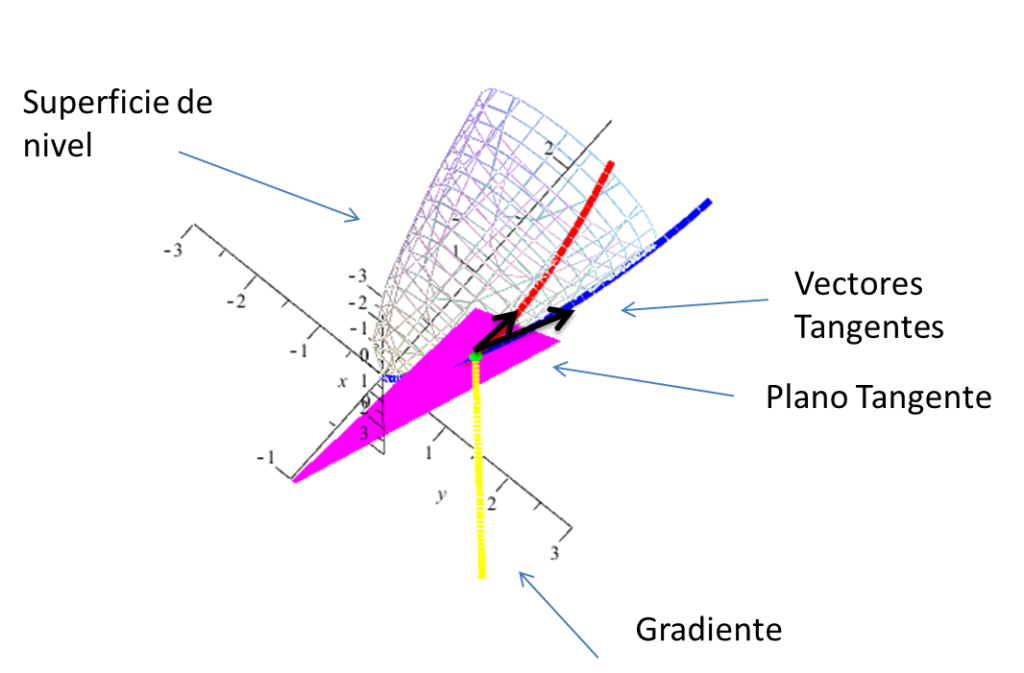
Dirección de Mayor Crecimiento de una Función
Teorema 5. Supongamos que $\nabla(f(x))\neq(0,0,0)$. Entonces $\nabla(f(x))$ apunta en la dirección a lo largo de la cual f crece más rápido.
Demostración. Si v es un vector unitario, la razón de
cambio de f en la dirección v está dada por $\nabla(f(x))\cdot v$ y
$\nabla(f(x)) \cdot v$ = $|\nabla{f(x)}|~|v|\cos\Theta$ = $|\nabla{f(x)}|\cos\Theta$,
donde $\Theta$ es el ángulo entre $\nabla{f}$, $v$. Este es máximo cuando $\Theta~=~0$ y esto ocurre cuando $v$, $~\nabla{f}$ son paralelos. En otras palabras, si queremos movernos en una dirección en la cual $f$ va a crecer más rápidamente, debemos proceder en la dirección $\nabla{f(x)}$. En forma análoga, si queremos movernos en la dirección en la cual $f$ decrece más rápido, habremos de proceder
en la dirección $-\nabla{f}$.
Ejemplo. Encontrar la dirección de rapido crecimiento en $(1,1,1)$ para $\displaystyle{f(x,y,z)=\frac{1}{\sqrt{x^{2}+y^{2}+z^{2}}}}$
Solución. En este caso
$$\nabla f(1,1,1)=\left(\frac{\partial \left(\frac{1}{\sqrt{x^{2}+y^{2}+z^{2}}}\right)}{\partial x},\frac{\partial \left(\frac{1}{\sqrt{x^{2}+y^{2}+z^{2}}}\right)}{\partial y},\frac{\partial \left(\frac{1}{\sqrt{x^{2}+y^{2}+z^{2}}}\right)}{\partial z}\right)\left|_{(1,1,1)}\right.=$$
$$\left(-\frac{x}{\sqrt{x^{2}+y^{2}+z^{2}}},-\frac{y}{\sqrt{x^{2}+y^{2}+z^{2}}},-\frac{z}{\sqrt{x^{2}+y^{2}+z^{2}}}\right)\left|_{(1,1,1)}\right.=-\frac{1}{3\sqrt{3}}\left(1,1,1\right)$$
Podemos tomar
$$u=\frac{\nabla f}{|\nabla f|}$$
en este caso
$$u=\frac{-\frac{1}{3\sqrt{3}}\left(1,1,1\right)}{\frac{1}{3}}=\left(-\frac{1}{\sqrt{3}},-\frac{1}{\sqrt{3}},-\frac{1}{\sqrt{3}}\right)$$
Puntos Estacionarios
Definición. Sea $f:\Omega\subset \mathbb{R}^{n} \rightarrow \mathbb{R}$ diferenciable, a los puntos $x\in \Omega$ tales que $\nabla f(x)=0$ se les llama puntos críticos (o punto estacionario) de la función.
Ejemplo. Sea $f:\mathbb{R}^{2}\rightarrow\mathbb{R}$ dada por $f(x,y)=x^{2}-y^{2}$ hallar los puntos críticos de $f$
Solución. Se tiene que $\nabla f(x)=(2x, 2y)$ \hspace{0.5cm}$\nabla f(x)=0\Leftrightarrow(2x, 2y)=(0,0)\Leftrightarrow 2x=0$ y $2y=0\Leftrightarrow x=0$ y $y=0$ \hspace{0.5cm} $\therefore$ $(0,0)$ es el único punto crítico de $f$.
Ejemplo. Que condición se debe satisfacer para que la función $f:\mathbb{R}^{2}\rightarrow\mathbb{R}$ dada por $f(x,y)=ax^{2}+2bxy+cy^{2}+dx-ey+f$ tenga un punto crítico
$\nabla f=(2ax+2by+d, 2bx+2cy-e)$ entonces
$\nabla f=0\Leftrightarrow 2ax+2by+d=0$ y $2bx+2cy-e=0$
$\Rightarrow$ $ 2ax+2by=-d$ y $2bx+2cy=e$ se necesita que
$\Rightarrow$ $2a(2c)-(2b)^{2}\neq 0$ $\therefore$ $ac-b^{2}\neq 0$
Mas adelante
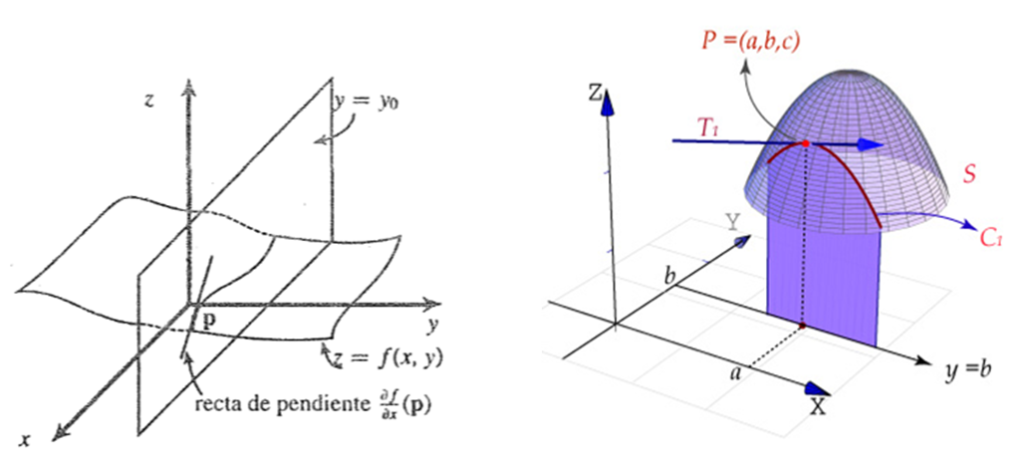
En la siguiente entrada veremos como la regla de la cadena representa una herramienta del cálculo que permite derivar funciones compuestas. Si una variable depende de otra, y esa a su vez depende de otra, la derivada de la función final se obtiene multiplicando las derivadas intermedias. También veremos cómo gracias a que el gradiente representa la dirección de máximo crecimiento nos ayuda a definir el plano tangente de una función en un punto dado.
Tarea Moral
1.- Sea la función $f:\mathbb{R^2}\rightarrow \mathbb{R}$ con $f:xe^y$ calcula: $\nabla f=(\frac{\partial{f}}{\partial{x}}, \frac{\partial{f}}{\partial{y}}, \frac{\partial{f}}{\partial{z}})$
2.- Sea $f(x,y)=x^2+y+3y^2$ calcula la derivada direccional en el punto $(2,-4)$ en la dirección $(3,2)$.
3.- Evalua el gradiente de $f(x,y,z)=log(x^2+y^2+z^2)$ en $(1,0,1)$
4.- Sean $f,g:\mathbb{R}^2\rightarrow \mathbb{R}$ prueba que $\nabla(fg)=f \nabla g+ \nabla f g$
5.- Sea $f(x,y,z)=x^2e^{-yz}$ calcula la derivada direccional de $f$ en la dirección del vector unitario $v=(\dfrac{1}{3},\dfrac{1}{3},\dfrac{1}{3})$
Enlaces