Introducción
A lo largo de este capítulo, exploraremos el origen del concepto de pago de intereses y rastrearemos la evolución de los modelos matemáticos que describen los fenómenos de interés simple y compuesto. Abordaremos conceptos clave como el valor presente, tasas efectivas, tasas nominales, tasas instantáneas y sus características individuales. Además, examinaremos las interrelaciones entre estos conceptos. Al comprender estos fundamentos, obtendremos el conocimiento necesario para calcular tasas equivalentes.
Estos conceptos son fundamentales en el campo de las Matemáticas Financieras y proporcionan las herramientas esenciales para desarrollar modelos más complejos que resuelvan problemas cotidianos en diversos ámbitos de la sociedad. Esto incluye situaciones como préstamos entre individuos, transacciones comerciales entre empresas y actividades gubernamentales en todos los sectores de la economía. La falta de comprensión de estos modelos puede tener un impacto directo en la situación financiera de cada individuo.
En términos simples, el interés es el costo que se incurre al hacer uso de los recursos ajenos. Para el propósito de nuestro estudio, la mayoría de las veces, estos recursos serán dinero.
El objetivo principal de las Matemáticas Financieras es desarrollar modelos matemáticos que describan este fenómeno social que hemos mencionado. Para lograrlo, examinaremos cómo se realizan los pagos de intereses y analizaremos las variables involucradas en esta actividad, considerando cómo interactúan a lo largo del tiempo.
En un préstamo típico, se pueden identificar dos actores principales: el prestamista (quien presta el bien o el dinero) y el prestatario (también conocido como acreditado, que recibe el préstamo). La compensación que regularmente se conoce como intereses.
El fenómeno que vamos a estudiar implica que una persona presta dinero a otra durante un período determinado, y durante ese tiempo, la persona que recibe el préstamo debe pagar una cierta cantidad de intereses al prestamista. A partir de esto, podemos identificar las siguientes variables clave:
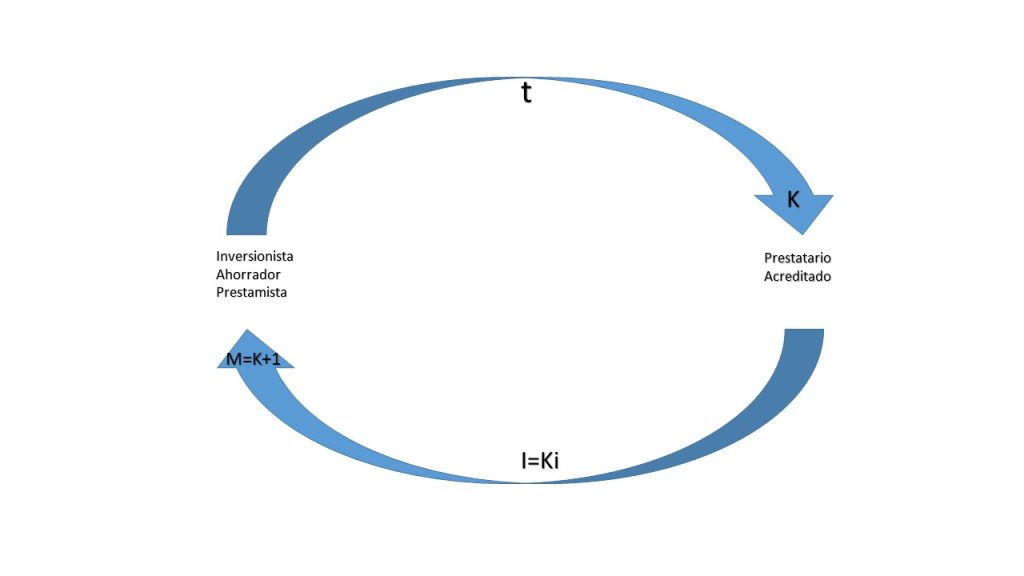
Donde:
- $K$ es el valor del bien, dinero o capital, prestado o invertido.
- $i$ es la tasa de interés que el prestamista y el prestatario han acordado como compensación o premio por el capital prestado y recibido. Cabe hacer mención que generalmente se manejan las tasas de interés en términos de porcentaje (%), con el objeto de generalizar y de simplificar, la determinación del interés por pagar. La tasa de interés se define como: la proporción que por unidad de capital y de tiempo, habrá de pagarse por disfrutar de un préstamo. En dicha tasa se debe de establecer la periodicidad con la cual se va a estar pagando, esto es, anual, mensual, semanal, diaria, instantánea, etc.
- $I$ representa los intereses, en dinero, que recibirá el prestamista por el capital prestado o invertido y que resultan de multiplicar la tasa de interés $i$, expresada en porcentaje, por el capital $K$, es decir $Ki$.
- $M$ es la suma del capital invertido más los intereses ganados, esto es; $K+I$, y se le conoce con el nombre de monto.
- $t$ es el tiempo, plazo o duración que dure la operación. Es decir, el tiempo total que han convenido el prestamista y el prestatario para que este último disfrute del préstamo. Es importante señalar que las unidades de tiempo $t$, estarán dadas de acuerdo con la periodicidad con la que se pague la tasa. Si la tasa es mensual y el préstamo es a un año, entonces t tendrá un valor de 12, que equivale al número de meses que tiene un año.
Las Matemáticas Financieras, tienen por objeto estudiar la relación que hay entre las variables anteriores, y construir modelos que expliquen y describan dicho fenómeno del pago de intereses, cuya representación gráfica se muestra a continuación:

Tenemos entonces:
- $K=$ Capital
- $i =$ tasa de Interés
- $M =$ Monto (Capital prestado más los intereses)
- $t =$ Tiempo
- $I =$ Intereses (Capital multiplicado por la tasa de interés acordada)
Es importante señalar, que el «apellido» inseparable del valor de la «tasa» es la temporalidad o periodicidad con que deberá ser pagada, de tal forma que no quede duda de cada cuándo se realizará el negocio.
Por ejemplo, imaginemos que una persona A le presta dinero a una persona B de \$1000, y en compensación B le pagará \$100 pesos por concepto de intereses al mes. Ante tal situación la cantidad a pagar después de haber transcurrido dicho mes es de \$1100. Lo anterior lo podemos expresar como:
- \$1000 que es el capital originalmente prestado, es decir el valor de $K$
- \$1100 qué es valor de $M =$ La suma del capital más los intereses.
- \$1100 – \$1000 = \$100 es la cantidad de intereses generados durante un mes.
Para determinar la tasa de interés efectiva por periodo, esto es, la proporción de intereses ganados por unidad de capital y tiempo, dividimos los intereses ganados entre el capital. Esto se puede escribir como:
$$\frac{M-K}{(K)(t)}=\frac{1100-1000}{(1000)(1)}=0.10.$$
Es decir, el interés obtenido es equivalente al 10% efectivo mensual. La palabra efectivo o efectiva se utiliza para especificar la tasa a la que califica, y corresponde a la que se pagará por unidad de capital y tiempo.
Como se ha mencionado previamente, la periodicidad de la tasa determina la frecuencia con la que se pagarán los intereses. Estos pagos pueden realizarse a discreción, ya sea cada hora, diariamente, mensualmente, semestralmente, anualmente, cada cinco años, u otras opciones.
Además de los actores y las variables que influyen en cualquier transacción financiera, existe un último elemento digno de análisis: la elección con respecto al destino de los intereses, es decir, si se reinvierten o no.
Por otro lado, el término «efectiva» cumple la función de diferenciar este tipo de tasas de otras denominadas «nominales», que operan de manera distinta, como se detallará más adelante.
Estas dos alternativas se conocen como interés compuesto (cuando los intereses generan nuevos intereses) e interés simple (cuando los intereses no generan nuevos intereses).
A continuación, se va a construir el modelo sobre el interés simple.
Interés Simple
Se abordará este tema con fines comparativos, dado que, en la actualidad, el modelo de interés simple tiene una aplicación cada vez más limitada.
Una de las características clave de este modelo es que los intereses generados por el capital no generan intereses adicionales.
Supongamos que una persona A le presta a una persona B \$100.00 y pactan una tasa de interés del 10% mensual. Una vez transcurrido el primer mes, la persona B le tiene que pagar a la persona A un rendimiento de \$10.00 por concepto de intereses, proceso que se repetirá hasta que se termine el plazo que hayan acordado entre ambas partes involucradas para regresar el dinero prestado. Vamos a suponer que el tiempo acordado es de 5 meses. Esto implica que al final del segundo mes, la persona B tendrá que realizar el pago de los siguientes intereses, los cuales ascienden a nuevamente otros \$10.00.
Dicho proceso se irá repitiendo exactamente igual durante los siguientes 3 meses, de tal forma que la persona B habrá pagado a la persona A una cantidad total de \$50.00 de intereses. Entonces, el capital más los intereses sumarían una cantidad de \$150.00
Observemos que, si al final de cada mes la persona B le paga los intereses a la persona A, dichos intereses no generan nuevos intereses, dichos intereses ya están en manos de la persona A, motivo por el cual ya no tienen por qué seguir cobrando intereses a la persona B por una cantidad que ya no adeuda.
Sin embargo, puede darse el caso que la persona A haya convenido con la persona B, que la cantidad generada por motivo de intereses (\$50.00), la pagará al final de los 5 meses a la tasa convenida del 10% mensual y que, además, la operación se realizaría bajo el modelo de interés simple. En dicho caso, la cantidad que se genera a partir del concepto de intereses será conservada por parte de la persona B, hasta el término del plazo pactado.
En dicho caso, se observa que la cantidad generada por concepto de intereses sigue estando en manos de la persona B, entonces esto implicaría que dicha persona debería también pagar intereses sobre esos intereses. Sin embargo, esto no ocurre así, dado que la operación se está realizando bajo el modelo de interés simple y, por ello, la persona sólo pagará al final de los 5 meses el capital prestado (\$100) más la suma aritmética de los intereses mensuales (\$50).
Es aquí donde surge la diferencia entre el modelo de interés simple y el compuesto. En el primer caso los intereses no generan nuevos intereses, aunque no se hayan pagado; mientras que, en el segundo, si los intereses no se pagan, pasarían a formar parte del capital prestado y producirían nuevos intereses.

En la figura 1.3 se observa que en el modelo del interés simple la recta horizontal representa el tiempo, la cual está seccionada en partes iguales que son los periodos en que los intereses serán pagados. El número de periodos está determinado por la temporalidad o periodicidad de la tasa de interés, si la tasa es efectiva mensual, los periodos serán meses, si es anual serán años, y así sucesivamente según sea el caso.
Al final de cada periodo (en este caso al final de cada mes), se describen los cálculos que se realizan para determinar el monto alcanzado hasta esa fecha, por ejemplo, el monto final del segundo periodo está dado por el monto del periodo inmediato anterior $M = K(1+i),$ más los intereses devengados por el capital del original durante el segundo periodo, el cual es: $M = K(1+2i)$.
También en la figura 1.3 se muestran las operaciones para calcular el monto final de los periodos restantes, que como se puede apreciar, siguen un comportamiento análogo al que se ha estado utilizando para calcular los montos anteriores.
Con base en lo anterior, se puede deducir, que el modelo de interés simple para calcular el monto para el periodo t está representado por:
Si hacemos uso de esa fórmula y la aplicamos en el ejemplo anterior, pero modificando el periodo de 5 meses a 7, el resultado que se tendría luego de haber transcurrido dicho plazo es:
\begin{align*}
M&=100[1+ (0.1)(7)]\\
&=100[1+0.7]\\
&=170.
\end{align*}
Es de gran relevancia mencionar las características de las variables que aparecen en la fórmula de interés simple, las cuales son:
- Los valores que tienen las variables $M$ y $K$ son unidades monetarias (pesos, dolares, etc).
- La tasa de interés $i$ es en términos porcentuales (%), sin embargo, para fines prácticos será utilizada al tanto por uno, esto es ya dividida entre 100.
- La variable $t$ corresponde al tiempo al cual está determinado siempre por la periodicidad que esté manejando la tasa de interés. Si la tasa es mensual, la variable $t$ será establecida en meses.
Despejar otras variables de la fórmula de interés simple
A partir de la ecuación que se obtuvo para describir el modelo de interés simple, es posible hacer el cálculo de las demás variables expresándolas en términos de las demás, esto es, calcular las variables $K, i,$ y $t$ realizando los despejes que a continuación se ilustran.
Para obtener el valor de la variable $K$ tenemos:
Para expresar el valor de la tasa de interés $i$:
Partiendo de la expresión original, lo primero que debe hacerse es dividir entre $K$ ambos lados de la ecuación:
$$\frac{M}{K}=\frac{(1+it)}{K},$$
Luego, restar 1 de ambos lados de la ecuación:
$$\frac{M}{K}-1=it.$$
$$it=\frac{M-K}{K}.$$
Y, por último, dividir entre $t$ ambos lados de la ecuación:
$$\frac{it}{t}=\frac{M-K}{Kt}$$
$$i=\frac{M-K}{Kt}.$$
Ahora, para obtener $t$, se aplica el mismo razonamiento, para llegar a la siguiente expresión:
$$t=\frac{M-K}{Ki}.$$
Con esto se puede concluir que, es posible obtener el valor de cualquier variable, a partir de conocer las otras 3. De forma gráfica, el modelo de interés simple queda descrito por una línea recta, tal y como se representa en la figura 1.4:

En donde, se observa que el eje $y$ representa el monto acumulado $M$, mientras que el eje de las $x$ representa el tiempo $t$, y la pendiente de la recta descrita representa el crecimiento del monto a través del tiempo, lo que equivale a la expresión $Ki$.
Ejercicios resueltos
Ejercicio. Si sabemos que el capital inicial es \$2000 y la tasa de interés es de 8% mensual, ¿Cuánto es el monto que obtendremos después de 5 periodos, con el modelo de interés simple?
Solución
Solución. Usando la fórmula sería:
$M=K(1+it)$
donde:
$K=\$2000$
$i=8\%=0.08$ mensual
$t=5$ meses
Sustituyendo cada uno de los valores de las variables en nuestro modelo de interés simple, nos queda:
$M=K(1+it)=2000[1+(0.08)(5)]=2800$
La respuesta es: Obtendremos un monto de $\$2800$.
Ejercicio. Una persona prestó \$3000 a otra que ofrece pagarle \$6000 después de 6 meses. ¿Cuál es la tasa de interés anual que se está ganando?
Solución
Para este problema necesitaremos la fórmula $M=K(1+it)$.
Sustituyendo los valores que nos han proporcionado tenemos:
$6000=3000[1+i(0.5)]$
Usando la ecuación que obtuvimos para encontrar la tasa de interés, nos queda:
\begin{align*}
i&=\frac{6000-3000}{[3000(0.5)]}\\
&= \frac{3000}{18000}=200
\end{align*}
Observación. Por ser una tasa anual, y al tener un plazo de 6 meses, tenemos que considerar la mitad de dicha tasa, ya que es la mitad del año.
Por lo tanto el resultado es: Se está pagando una tasa de interés del 200%.
Ejercicio. ¿Cuánto debo invertir?, para que dentro de 1 año, bajo el modelo de interés simple, obtenga una cantidad \$10000, si el banco me paga una tasa del 5% mensual.
Solución
De nuestra ecuación de interés simple, directamente vamos a utilizar la ecuación que deducimos previamente:
$$K=\frac{M}{(1+i)}$$
Sustituyendo cada uno de los datos tenemos:
$$K=\frac{10000}{(1+(0.05)(12))}$$
Entonces se tendría que invertir la cantidad de \$6250.
Más adelante…
En esta entrada hemos discutido los antecedentes de las matemáticas financieras, abordando el tema del interés simple, su proceso de construcción, y finalmente deducimos la ecuación que describe este fenómeno. También exploramos el concepto de interés simple y presentamos algunos ejercicios resueltos. Aunque el interés simple es intrigante, en muchas ocasiones deseamos no solo reinvertir el capital inicial, sino también los intereses acumulados. Esto nos lleva al próximo tema que exploraremos en la siguiente entrada: el concepto de interés compuesto.
Entradas relacionadas
- Ir a Matemáticas Financieras
- Entrada siguiente:Matemáticas Financieras: Interés compuesto

Después de este curso sería excelente que prepararan notas sobre un diplomado que se impartió en la Facultad de Ciencias «Finanzas Corporativas y Bursátiles» .
Gracias
Hola Hiram. No conozco ese diplomado que mencionas, pero quizás se pueda averiguar al respecto y ver si los profesores que lo imparten están interesados en tener sus notas así. Tal vez sea un poco difícil pues creo que esos diplomados luego son más con fines de que la gente se inscriba y pague una cuota, entonces no que qué tan abiertos estén a la idea de poner material abierto y gratuito. Pero bueno.