Definición 1: (en términos de sucesiones)
Sea $f: A\subseteq \mathbb{R}^n \longrightarrow \mathbb{R}^m$.
Sea $\overrightarrow{x_0}$ un punto de acumulación de $A$. Sea $\overrightarrow{L} \in \mathbb{R}^m.$
Decimos que $\overrightarrow{L}$ es el límite de $f$ cuando $\overrightarrow{x} \longrightarrow \overrightarrow{x_0}$ con $\overrightarrow{x} \in A$ si para toda sucesión $\Big\{ \overrightarrow{x_n} \Big\} \longrightarrow \overrightarrow{x_0}$ con puntos $\overrightarrow{x_n} \in A$, con $\overrightarrow{x_n} \neq \overrightarrow{x_0}$ resulta que la sucesión $\Big\{f \Big(\overrightarrow{x_n} \Big) \Big\} \longrightarrow \overrightarrow{L}$
Observación: como la noción de convergencia de una sucesión vale en espacios métricos, esta será nuestra definición de límite de una función $f : X \longrightarrow Y$ con $\Big(X, d_x\Big)$ y $\Big(Y, d_y\Big)$ espacios métricos.
El concepto de límite nos permite dar un concepto de continuidad de una función en un punto.
Sea $f : A \subseteq \mathbb{R}^n \longrightarrow \mathbb{R}^m$.
Sea $\overrightarrow{x_0} \in A$.
Decimos que $f$ es continua en $\overrightarrow{x_0}$ si para toda sucesión $\Big\{ \overrightarrow{x_n}\Big\} \in A$ tal que $\Big\{ \overrightarrow{x_n} \Big\}$ converge a $\overrightarrow{x_0}$ resulta que $ \Big\{ f \Big( \overrightarrow{x_n} \Big) \Big\} \longrightarrow f \Big(\overrightarrow{x_0} \Big).$ En otras palabras, $f$ es continua $ \overrightarrow{x_0}$ si existe el límite de $f$ cuando $\overrightarrow{x}$ tiende a $\overrightarrow{x_0}$ y este límite es igual a $f \Big(\overrightarrow{x_0} \Big).$
Definición 2: $\big($ en términos de $\epsilon$ y $\delta$ $\big)$
$\overrightarrow{L}$ es el límite de $f$ cuando $\overrightarrow{x} \longrightarrow \overrightarrow{x_0}$ si $$\forall \, \epsilon > 0 \, \exists \, \delta > 0\, \text{ tal que} \; 0 < \Big\|\overrightarrow{x}\, -\, \overrightarrow{x_0} \Big\| < \delta \Longrightarrow \Big\|f( \overrightarrow{x})\, -\, \overrightarrow{L} \Big\| < \epsilon$$
Decimos que $f$ es continua en $\overrightarrow{x_0}$ si $\forall \, \epsilon > 0 \; \exists\, \delta > 0$ tal que $ \Big\|\overrightarrow{x}\, -\, \overrightarrow{x_0} \Big\| < \delta$ implica que $\Big\|f \Big( \overrightarrow{x} \Big) \, – \, f \Big(\overrightarrow{x_0} \Big) \Big\| < \epsilon.$
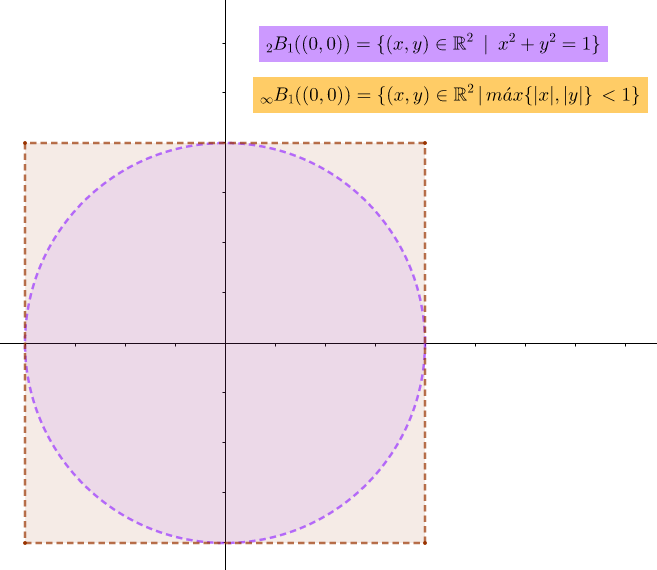
Definición 3: (en términos de bolas abiertas)
$\overrightarrow{L}$ es el límite de $f$ cuando $\overrightarrow{x} \longrightarrow \overrightarrow{x_0}$ si para toda bola de radio $\epsilon > 0$ centrada en $\overrightarrow{L}$ existe una bola perforada de radio $\delta > 0$ centrada en $\overrightarrow{x_0}$ tal que $\overrightarrow{x} \in \mathring{B}_{\delta} \Big(\overrightarrow{x_0} \Big)$implica que $f \Big(\overrightarrow{x} \Big) \in B_{\epsilon} \Big(\overrightarrow{L} \Big).$
Decimos que $f$ es continua en $\overrightarrow{x_0}$ $\iff$ para toda bola de radio $\epsilon > 0$ centrada en $\overrightarrow{L}$ existe una bola de radio $\delta > 0$ centrada en $\overrightarrow{x_0}$ tal que $\overrightarrow{x} \in B_{\delta} \Big( \overrightarrow{x_0} \Big) \Longrightarrow f \Big( \overrightarrow{x} \Big) \in B_{\epsilon} \Big( f \Big(\overrightarrow{x_0} \Big) \Big).$
Lema: definición (3) es equivalente a la definición (2).
Clave para la demostración:
$f \Big(\overrightarrow{x}\Big) \in B_{\epsilon} \Big(\overrightarrow{L} \Big) \iff \Big\|\, f \Big(\overrightarrow{x}\Big) \, – \, \overrightarrow{L}\Big\| < \epsilon$
$\overrightarrow{x} \in B_{\delta} \Big(\overrightarrow{x_0} \Big) \iff \, \Big\| \overrightarrow{x}\, – \, \overrightarrow{x_0} \Big\| < \delta$
Basta probar que la definición (1) es equivalente con la definición (3).
Teorema: la definición (1) es equivalente a la definición (3).
Demostración:
$\big[$ definición (1) $\longrightarrow$ definición (3) $\big]$
Hipótesis: $\forall \, \Big\{\overrightarrow{x_n} \Big\} \longrightarrow \overrightarrow{x_0} , \; \text{con } \overrightarrow{x_n} \neq \overrightarrow{x_0}$ se tiene que $\Big\{ f \Big( \overrightarrow{x_n} \Big) \Big\} \longrightarrow \overrightarrow{L}$
$\big[$ por demostrar: $\forall \, \epsilon > 0 \; \exists \, \delta > 0$ tal que si $\overrightarrow{x} \in \mathring{B}_{\delta} \Big(\overrightarrow{x_0} \Big), \text{ entonces } f \Big(\overrightarrow{x} \Big) \in B_{\epsilon} \Big(\overrightarrow{L} \Big) \big]$
Supongamos que $f$ no tiene límite $\overrightarrow{L}$ con la definición de bolas.
Vamos a tratar de contradecir el hecho de que cumpla la definición de sucesiones.
$\exists \; \epsilon_0 > 0$ tal que $\forall\, \delta > 0 \; \exists \, \overrightarrow{x} \in \mathring{B}_{\delta} \Big(\overrightarrow{x_0} \Big) \, \land \, f \Big(\overrightarrow{x} \Big) \notin B_{\epsilon} \Big(\overrightarrow{L}\Big)$
Esto sucede en particular para $\delta = \frac{1}{n}$, entonces $\exists \, \overrightarrow{x_n} \in \mathring{B}_{\frac{1}{n}} \Big(\overrightarrow{x_0} \Big) \, \land \, f \Big(\overrightarrow{x_n} \Big) \notin B_{\epsilon} \Big(\overrightarrow{L} \Big).$ Entonces existe una sucesión $\Big\{\overrightarrow{x_n}\Big\} \longrightarrow \overrightarrow{x_0}$ para la cual $\Big\{ f \Big(\overrightarrow{x_n}\Big) \Big\}$ no converge.
$\big[$ definición (3) $\longrightarrow$ definición (1) $\big]$
Hipótesis: $\forall \, \epsilon > 0 \; \exists \, \delta > 0$ tal que $\overrightarrow{x} \in \mathring{B}_{\delta} \Big(\overrightarrow{x_0} \Big) \Longrightarrow f \Big(\overrightarrow{x} \Big) \in B_{\epsilon} \Big(\overrightarrow{L} \Big)$
$\big[$ por demostrar: $\forall \, \Big\{\overrightarrow{x_n} \Big\} \longrightarrow \overrightarrow{x_0} , \; \text{con } \overrightarrow{x_n} \neq \overrightarrow{x_0}$ se cumple que $\Big\{ f \Big( \overrightarrow{x_n}\Big) \Big\} \longrightarrow \overrightarrow{L}\big]$
Sea $\Big\{\overrightarrow{x_n}\Big\} \longrightarrow \overrightarrow{x_0}$ con $\overrightarrow{x_n} \neq \overrightarrow{x_0}$
$\big[$por demostrar: $\Big\{f \Big(\overrightarrow{x_n}\Big)\Big\} \longrightarrow \overrightarrow{L} \big]$
Sea $\epsilon > 0$
$\big[$ por demostrar: $\exists \, N \in \mathbb{N}$ tal que $n \geq N \Rightarrow f \Big(\overrightarrow{x_n} \Big) \in B_{\epsilon} \Big(\overrightarrow{L} \Big) \big]$
Dada la $\epsilon > 0$ (por hipótesis), existe $\delta > 0$ tal que $\overrightarrow{x} \in \mathring{B}_{\delta} \Big(\overrightarrow{x_0} \Big) \Longrightarrow f \Big(\overrightarrow{x} \Big) \in B_{\epsilon} \Big(\overrightarrow{L} \Big).$
Luego la sucesión $\Big\{ \overrightarrow{x_n} \Big\} \longrightarrow \overrightarrow{x_0}$ entonces para la $\delta > 0$ recién dada $\exists \; Ñ \in \mathbb{N}$ tal que $n \geq Ñ \Rightarrow \overrightarrow{x_n} \in B_{\delta} \Big(\overrightarrow{x_0} \Big)$.
Más aún, como $\overrightarrow{x_n} \neq \overrightarrow{x_0}, \text{ se cumple que } \; \overrightarrow{x_n} \in \mathring{B}_{\delta} \Big(\overrightarrow{x_0} \Big) \text{ podemos concluir que } f \Big(\overrightarrow{x_n} \Big) \in B_{\epsilon} \Big(\overrightarrow{L} \Big).$
Sirve $N=Ñ$ por lo que $\exists \; N \in \mathbb{N}$ tal que para toda $n > N$ se cumple que $f \Big(\overrightarrow{x_n} \Big) \in B_{\epsilon} \Big(\overrightarrow{L} \Big).\; _{\blacksquare}$