Introducción
En las entradas pasadas introdujimos los conceptos de variable aleatoria y función de distribución. Además, al final de la entrada pasada comentamos que las variables aleatorias pueden clasificarse como discretas o continuas, dependiendo de la cardinalidad del conjunto de valores que pueden tomar.
En esta entrada trataremos el caso de las variables aleatorias discretas. En el contexto de las matemáticas se usa el término «discreta» para hacer referencia a conjuntos finitos o infinitos numerables. Por ello, a grandes rasgos, las variables aleatorias discretas son aquellas cuyo conjunto de valores que pueden tomar es a lo más infinito numerable.
¡IMPORTANTE! Algunas convenciones que usaremos
De ahora en adelante, escribiremos «variable aleatoria» simplemente como v.a. De este modo, por ejemplo, cuando digamos «sea $X$ una v.a.», deberás de leerlo como «sea $X$ una variable aleatoria».
Por otro lado, usaremos los límites laterales (por la derecha y por la izquierda) de la función de distribución, por lo que introduciremos la siguiente notación: si $F\colon\RR\to\RR$ es una función, entonces
\begin{align*}F(a+) &:= \lim_{x\to a^{+}} F(x), \\ F(a-) &:= \lim_{x\to a^{-}} F(x). \end{align*}
En otras palabras,
- $F(a+)$ es el límite de $F(x)$ cuando $x$ tiende a $a$ por la derecha.
- $F(a-)$ es el límite de $F(x)$ cuando $x$ tiende a $a$ por la izquierda.
Esta convención facilita la escritura de las fórmulas que involucran a estos límites.
Definición de variable aleatoria discreta
Como su nombre lo indica, una v.a. discreta es aquella v.a. cuyo conjunto de valores que puede tomar es un conjunto de cardinalidad a lo más numerable. Es decir, que la cantidad de valores distintos que puede tomar la v.a. es finito, o infinito numerable.
Definición. Sea $X$ una v.a. sobre $(\Omega, \mathscr{F}, \mathbb{P})$. Diremos que $X$ es una variable aleatoria discreta si el conjunto de valores que puede tomar $X$ es finito o infinito numerable.
De manera más formal, un conjunto $S \in \mathscr{B}(\RR)$ es llamado un soporte de la v.a. $X$ si $\Prob{X \in S} = 1$. Así, $X$ es una v.a. discreta si tiene un soporte finito o infinito numerable.
Cuando $X$ es una v.a. discreta, y el conjunto de valores que toma $X$ es $\{ x_{n} \}_{n\in\mathbb{N}^{+}}$ de tal manera que $x_{n} < x_{n+1}$ para cada $n \in \mathbb{N}^{+}$, la función de distribución de $X$, $F_{X}$, es una función escalonada con una discontinuidad de magnitud $\Prob{X = x_{n}}$ en cada $x_{n}$. Además, $F_{X}$ es constante entre los $x_{n}$, y toma el valor mayor en cada discontinuidad. Esto es algo que puedes observar en el ejemplo 4 de la entrada anterior.
Además, si $X$ es una variable aleatoria cualquiera, se cumple que
\[ \Prob{X = a} = \Prob{X \leq a} − \Prob{X < a} = F_{X}(a) − F_{X}(a-). \]
En particular, cuando $X$ es una variable aleatoria discreta, $\Prob{X = a} > 0$ cuando $a$ es alguno de los valores que puede tomar $X$; y es $0$ en cualquier otro caso. La demostración de que $F_{X}(a-) = \Prob{X < a}$ te la dejamos como parte de la tarea moral.
Más aún, como vimos que la función de distribución de una v.a. contiene toda la información sobre una v.a. $X$, entonces si $X$ es una v.a. discreta, los valores $\Prob{X = a}$ para cada $a \in \RR$ capturan toda la información sobre el comportamiento probabilístico de $X$. ¡Cuidado! Esto sólamente pasa con las v.a.’s discretas, veremos que con las continuas no es así.
Función de masa de probabilidad de una v.a. discreta
A la función que manda a cada $a\in\RR$ al valor $\Prob{X=a}$ se le conoce como la función de masa de probabilidad (en inglés, probability mass function), que definimos a continuación.
Definición. Sea $X$ una v.a. discreta que toma los valores $\{ x_{n} \}_{n\in\mathbb{N}^{+}}$. Se define la función de masa de probabilidad (f.m.p.) de $X$, denotada por $p_{X}\colon\RR\to\RR$, como sigue.
\[ p_{X}(x) = \Prob{X = x}. \]
Esta función también es conocida simplemente como función de probabilidad.
Observa que $p_{X}(x) > 0$ cuando $x$ es alguno de los valores en $\{ x_{n} \}_{n\in\mathbb{N}^{+}}$; y $p_{X}(x) = 0$ en cualquier otro caso. De acuerdo con lo anterior, para cualquier $A \in \mathscr{B}(\RR)$ se tendrá que
\[ \Prob{X \in A} = \sum_{x\in A} p_{X}(x). \]
La suma anterior es discreta, pues $p_{X}(x)$ es mayor a $0$ en a lo más en una cantidad numerable de valores.
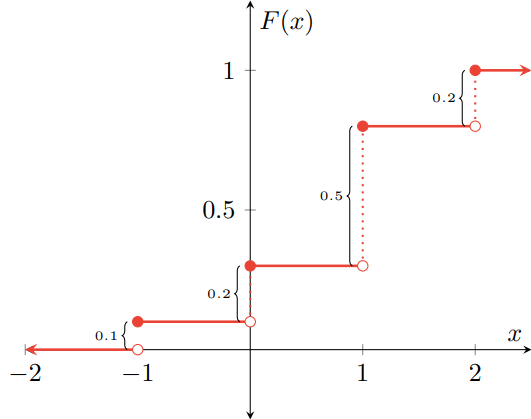
Ejemplo 1. Sea $X$ una v.a. con distribución $F\colon\RR\to\RR$ dada por
\[ F(x) = \begin{cases} 0 & \text{si $x < -1$,} \\[1em] 0.1 & \text{si $-1 \leq x < 0$,} \\[1em] 0.3 & \text{si $0 \leq x < 1$,} \\[1em] 0.8 & \text{si $1 \leq x < 2$,} \\[1em] 1 & \text{si $2 \leq x$.}\end{cases} \]
Es decir, la función de distribución de $X$ es $F$. Gráficamente, la función $F$ se ve como sigue:
Los puntos en los que $F$ presenta una discontinuidad son los valores que toma la variable aleatoria $X$, y la magnitud de los saltos es la probabilidad de que tome cada respectivo valor. La magnitud del salto corresponde precisamente a
\[ \Prob{X = a} = F(a) − F(a-), \]
pues en aquellos valores de $a$ en los que hay una discontinuidad, $F(a)$ y $F(a-)$ son valores distintos. Además, observa que para cada $a \in \RR$, $F(a)$ es la probabilidad acumulada por todos los valores menores o iguales a $a$. Por ejemplo, $F(-2) = 0$, que significa que $F$ no ha acumulado probabilidad hasta el valor $-2$. Es decir, todos los números reales menores o iguales a $-2$ acumulan $0$ de probabilidad. Por otro lado, $F(0) = 0.3$, por lo que la probabilidad acumulada hasta $0$ es de $0.3$. Esto es, los números reales que son menores o iguales a $0$ acumulan $0.3$ de la probabilidad.
A partir de la distribución $F$ podemos obtener la función de masa de probabilidad de $X$. Para ello, tenemos que usar la fórmula
\[ \Prob{X = a} = F(a) − F(a-). \]
Esta expresión es distinta de $0$ en todos los valores de $a$ en los que $F$ presenta una discontinuidad, y es $0$ en otro caso. En los puntos de discontinuidad se tiene que:
\begin{array}{lclclcl} \Prob{X =-1} &= & F(-1) − F((-1)-) & = & 0.1 − 0 & = & 0.1, \\
\Prob{X = 0} &= & F(0) − F(0-) & = & 0.3 − 0.1 & = & 0.2, \\
\Prob{X = 1} &= & F(1) − F(1-) & = & 0.8 − 0.3 & = & 0.5, \\ \Prob{X = 2} &= & F(2) − F(2-) & = & 1 − 0.8 & = & 0.2. \\ \end{array}
De este modo, la función de masa de probabilidad de $X$ es la función $p_{X}\colon\RR\to\RR$ dada por
\[ p_{X}(x) = \begin{cases} 0.1 & \text{si $x = -1$,} \\[1em] 0.2 & \text{si $x = 0$ o $x = 2$,} \\[1em] 0.5 & \text{si $x = 1$,} \\[1em] 0 & \text{en otro caso.} \end{cases} \]
Esto significa que la variable aleatoria $X$ toma valores en el conjunto $\{ -1, 0, 1, 2 \}$, que son precisamente los puntos en los que $F$ tiene una discontinuidad.
Conexión entre la función de masa de probabilidad y la función de distribución
En el ejemplo anterior puede observarse que la función de masa de probabilidad de $X$ contiene toda la información sobre el comportamiento probabilístico de $X$, pues gracias a ella podemos saber:
- El conjunto de valores que puede tomar $X$, que son aquellos cuya probabilidad es mayor a $0$.
- La probabilidad de que tome cada uno de estos valores.
Además, es posible recuperar la función de distribución de $X$ en cada $x \in \RR$ sumando los valores que toma $p_{X}$ hasta $x$.
\[ F(x) = \sum_{y \in (-\infty, x]} p_{X}(y). \]
La suma anterior tendrá a lo más una cantidad numerable de términos, pues $p_{X}(y) > 0$ en a lo más una cantidad numerable de valores. Además, como la función de masa de probabilidad permite recuperar una función de distribución, es suficiente con tener la f.m.p. para conocer el comportamiento probabilístico de una v.a. discreta. Por ello, usualmente en los ejercicios se te dará la función de masa de probabilidad.
Ejemplo 2. Una variable aleatoria que toma una cantidad infinita numerable de valores también es discreta. Por ejemplo, sea $Y$ una v.a. con función de masa de probabilidad $p_{Y}\colon\RR\to\RR$ dada por
\[ p_{Y}(y) = \begin{cases} \dfrac{1}{2^{y}} & \text{si $y \in \mathbb{N}^{+}$,} \\[1em] 0 & \text{en otro caso.} \end{cases} \]
De este modo, tenemos que
\begin{align*} p_{Y}(1) = \Prob{Y = 1} = \frac{1}{2^{1}} = \frac{1}{2}, \\[1em] p_{Y}(2) = \Prob{Y = 2} = \frac{1}{2^{2}} = \frac{1}{4}, \\[1em] p_{Y}(3) = \Prob{Y = 3} = \frac{1}{2^{3}} = \frac{1}{8}, \end{align*}
etcétera. Sin embargo, observa que ahora te estamos dando una función de masa de probabilidad, y no te damos una función de distribución. ¿Cómo podemos estar seguros de que la función que nos están dando representa el comportamiento probabilístico de manera correcta? Hay dos cosas de tenemos que revisar:
- Para cada $y \in \RR$, se debe de cumplir que $p_{Y}(y) \geq 0$. Recuerda, $p_{Y}(y)$ es una probabilidad, así que debe de ser mayor o igual a $0$.
- Que la suma de todos los valores que toma $p_{Y}$ es $1$. Esto debe de pasar porque la probabilidad de que $Y$ tome alguno de los valores que puede tomar debe de ser $1$.
La primera propiedad se cumple, pues $p_{Y}(y)$ es $0$ o una potencia de $\frac{1}{2}$. La segunda propiedad hay que verificarla. Para ello, hay que obtener
\[ \sum_{k=1}^{\infty} p_{Y}(k) = \sum_{k=1}^{\infty} {\left(\frac{1}{2}\right)}^{k}. \]
Podemos hacer uso de la fórmula para una serie geométrica, modificando un poco la expresión anterior. Así,
\begin{align*} \sum_{k = 1}^{\infty} {\left(\frac{1}{2}\right)}^{k} &= \sum_{k = 0}^{\infty} {\left(\frac{1}{2}\right)}^{k+1} \\[1em] &= \sum_{k = 0}^{\infty} {\left(\frac{1}{2}\right)}{\left(\frac{1}{2}\right)}^{k} \\[1em] &= {\left(\frac{1}{2}\right)} \sum_{k = 0}^{\infty} {\left(\frac{1}{2}\right)}^{k} \\[1em] \end{align*}
Así, nos queda una serie geométrica de la forma $\sum_{k=0}^{\infty} ar^{k}$, con $0 < r < 1$, por lo que resulta
\begin{align*} {\left(\frac{1}{2}\right)} \sum_{k = 0}^{\infty} {\left(\frac{1}{2}\right)}^{k} &= {\left(\frac{1}{2}\right)}{\left(\frac{1}{1 − \frac{1}{2} }\right)} \\[1em] &= {\left(\frac{1}{2}\right)}{\left(2\right)} \\[1em] &= 1.\end{align*}
Esto garantiza que $p_{Y}$ es una función que describe el comportamiento probabilístico de una v.a.
Podemos hacer el cálculo de probabilidades de $Y$. Por ejemplo, ¿cuál es la probabilidad de que $Y$ sea $2$ o sea $6$? Para verlo, tenemos que obtener la probabilidad de $(X =2) \cup (X = 6)$. Estos dos conjuntos son ajenos, pues
\[ (X = 2) \cap (X = 6) = X^{-1}[\{ 2 \}] \cap X^{-1}[\{ 6 \}] = X^{-1}[\{ 2 \} \cap \{ 6 \}] = X^{-1}[\emptyset] = \emptyset, \]
así que $\Prob{(X = 2) \cup (X = 6)} = \Prob{X = 2} + \Prob{X = 6}$. Así, tenemos que
\begin{align*} \Prob{(X = 2) \cup (X = 6)} &= \Prob{X = 2} + \Prob{X = 6} \\[1em]
&= p_{Y}(2) + p_{Y}(6) \\[1em] &= \frac{1}{2^{2}} + \frac{1}{2^{6}} \\[1em] &= \frac{1}{4} + \frac{1}{64} \\[1em] &= \frac{17}{64} \approx 0.2656, \\[1em] \end{align*}
así que la probabilidad de que $Y$ tome el valor $2$ o tome el valor $6$ es de aproximadamente $0.2656$, o $26.56\%$. Por otro lado, ¿cuál será la probabilidad de que $Y \leq 5$? Esta es la probabilidad de que tome alguno de los valores $1$, $2$, $3$, $4$ o $5$. En consecuencia, tenemos que
\begin{align*} \Prob{Y \leq 5} &= \Prob{Y = 1} + \Prob{Y = 2} + \Prob{Y = 3} + \Prob{Y = 4} + \Prob{Y = 5} \\[1em] &= \sum_{k=1}^{5} \Prob{Y = k} \\[1em] &= \sum_{k=1}^{5} p_{Y}(k) \\[1em] &= \sum_{k=1}^{5} {\left(\frac{1}{2}\right)}^{k} \\[1em] &= {\left(\frac{1}{2}\right)}\sum_{k=1}^{5} {\left(\frac{1}{2}\right)}^{k−1} \\[1em] &= {\left(\frac{1}{2}\right)}\sum_{k=0}^{4} {\left(\frac{1}{2}\right)}^{k} \\[1em] &= {\left(\frac{1}{2}\right)} {\left(\dfrac{1 − {\left(\frac{1}{2}\right)}^{4+1}}{1 − \frac{1}{2}}\right)} \\[1em] &= {\left(\frac{1}{2}\right)} {\left(\dfrac{1 − {\left(\frac{1}{2}\right)}^{5}}{\frac{1}{2}}\right)} \\[1em] &= {1 − {\left(\frac{1}{2}\right)}^{5}} = 0.96875, \end{align*}
así que la probabilidad de que $Y$ sea menor o igual a $5$ es de $0.96875$, o $96.875\%$. Otra pregunta interesante es, ¿cuál es la probabilidad de que $Y$ sea un número par? Es decir, si $P$ es el conjunto de números naturales pares,
\[ P = \{ n \in \mathbb{N}^{+} \mid \exists k \in \mathbb{N}\colon n = 2k \}, \]
¿cuál es el valor de $\Prob{Y \in P}$? Para verlo, observa que como en las probabilidades anteriores, la probabilidad que queremos calcular puede verse como la suma de las probabilidades de todos los valores en $P$. De este modo, se tiene que
\begin{align*} \Prob{Y \in P} &= \sum_{n \in P} \Prob{Y = n} \\[1em] &= \sum_{k = 1}^{\infty} \Prob{Y = 2k} \\[1em] &= \sum_{k = 1}^{\infty} p_{Y}(k) \\[1em] &= \sum_{k=1}^{\infty} {\left(\frac{1}{2}\right)}^{2k} \\[1em] &= {\left(\frac{1}{2}\right)}^{2}\sum_{k=1}^{\infty} {\left(\frac{1}{2}\right)}^{2k−2} \\[1em] &= {\left(\frac{1}{2}\right)}^{2}\sum_{k=1}^{\infty} {\left(\frac{1}{2}\right)}^{2(k−1)} \\[1em] &= {\left(\frac{1}{2}\right)}^{2}\sum_{k=1}^{\infty} {\left(\frac{1}{2^{2}}\right)}^{k−1} \\[1em] &= {\left(\frac{1}{2}\right)}^{2}\sum_{k=1}^{\infty} {\left(\frac{1}{4}\right)}^{k−1} \\[1em] &= {\left(\frac{1}{2}\right)}^{2}\sum_{k=0}^{\infty} {\left(\frac{1}{4}\right)}^{k} \\[1em] &= {\left(\frac{1}{4}\right)}{\left(\dfrac{1}{1 − \frac{1}{4}}\right)} \\[1em] &= {\left(\frac{1}{4}\right)}{\left(\dfrac{1}{\frac{3}{4}}\right)} \\[1em] &= {\left(\frac{1}{4}\right)}{\left(\dfrac{4}{3}\right)} = \frac{1}{3},\end{align*}
así que la probabilidad de que $Y$ tome como valor un número par es de $\frac{1}{3}$, o $33.333\ldots\%$.
Finalmente, observa que $\mathbb{N}$ y $\mathbb{N}^{+}$ son soportes de $Y$, pues $\Prob{Y \in \mathbb{N}^{+}} = 1$, y como $\mathbb{N}^{+} \subseteq \mathbb{N}$, se tiene que $\Prob{Y \in \mathbb{N}^{+}} \leq \Prob{Y \in \mathbb{N}}$, que implica $\Prob{Y \in \mathbb{N}} = 1$. Esto exhibe que cuando $S$ es un soporte de una v.a. discreta, está asegurado que contiene a todos los valores que puede tomar la v.a., pero no significa que todos los elementos de $S$ tienen probabilidad positiva. Por ejemplo, en este caso tenemos que $\Prob{Y = 0} = 0$ y $0 \in \mathbb{N}$.
Propiedades de una función de masa de probabilidad
Como vimos en el ejemplo anterior (y en la discusión que le precede), la función de masa de probabilidad es suficiente para conocer el comportamiento probabilístico de una v.a. discreta. Por ello, es necesario saber qué propiedades necesita una función cualquiera para ser la función de masa de probabilidad de alguna v.a. discreta $X$.
Sea $p\colon\RR\to\RR$ una función y sea $S = \{ \, s_{i} \mid i \in I \, \} \in \mathscr{B}(\RR)$ un conjunto a lo más numerable de números reales y sea $\{ \pi_{i} \mid i \in I \}$ una colección de números reales tales que
- Para cada $i \in I$ se cumple que $\pi_{i} \geq 0$.
- Se cumple que\[ \sum_{i \in I} \pi_{i} = 1, \]
si definimos $p\colon\RR\to\RR$ como
\[ p(x) = \begin{cases} \pi_{i} & \text{si $x = s_{i}$, con $i \in I$,} \\[1em] 0 & \text{si $x \notin S$,}\end{cases} \]
entonces existe una v.a. discreta $X$ tal que $p$ es la función de masa de probabilidad de $X$. En efecto, al tomar $F\colon\RR\to\RR$ dada por
\[ F(x) = \sum_{s \in (-\infty, x]} p(s), \quad \text{para cada $x \in \RR$,} \]
se tiene que $F$ es una función de distribución, así que la existencia de $X$ está garantizada por lo que vimos en la entrada de Funciones de Distribución.
En conclusión, si tu cuentas con una colección a lo más numerable $S = \{ \, s_{i} \mid i \in I \, \}$ de números reales, y $\{ \, \pi_{i} \mid i \in I \, \}$ son números reales que se pueden usar como la probabilidad de los elementos de $S$ (de tal manera que $\pi_{i}$ es la probabilidad de $s_{i}$), estos valores definen las probabilidades de que alguna v.a. discreta tome los valores en $S$.
Esto es, existe una v.a. discreta $X$ tal que
\begin{align*} \Prob{X = s_{i}} &= \pi_{i}, \quad \text{para cada $i \in I$.}\end{align*}
Fórmula para la función de distribución a partir de la función de masa de probabilidad
Más adelante veremos algunas v.a.’s que tienen a $\mathbb{N}$ como un soporte. Esto es, la probabilidad de que esas v.a.’s caigan en $\mathbb{N}$ es $1$. Por ello, el conjunto de valores que puede tomar una v.a. de ese tipo es el conjunto de los números naturales, o algún subconjunto de este, como $\mathbb{N}^{+}$ o $\{ 0, 1, \ldots, n \}$, para algún $n \in \mathbb{N}^{+}$. Por ejemplo, ya vimos que $\mathbb{N}$ es un soporte de la v.a. $Y$ del último ejemplo; aún cuando el conjunto de valores que puede tomar $Y$ es $\mathbb{N}^{+}$.
En tales casos, la función de distribución de una v.a. discreta puede escribirse a partir de la función de masa de probabilidad de manera ordenada como sigue. Si $X$ es una v.a. discreta tal que su función de masa de probabilidad es $p_{X}\colon\RR\to\RR$ dada por
\[p_{X}(x) = \begin{cases} \pi_{x} & \text{para cada $x \in \mathbb{N}$,} \\[1em] 0 & \text{si $x \notin \mathbb{N}$}, \end{cases} \]
donde $\{ \pi_{i} \mid i \in \mathbb{N} \}$ son números reales tales que $\pi_{i} \geq 0$ para cada $i \in \mathbb{N}$ y $\sum_{k=0}^{\infty} \pi_{k} = 1$. Entonces la función de distribución de $X$ puede escribirse como
\[ F_{X}(x) = \begin{cases} 0 & \text{si $x < 0$,} \\[1em] \pi_{0} + \pi_{1} + \cdots + \pi_{\lfloor x \rfloor} & \text{si $x \geq 0$}. \end{cases} \]
donde $\lfloor x \rfloor$ es el mayor entero que es menor o igual a $x$. Por ejemplo, $\lfloor \pi \rfloor = 3$ y $\lfloor 6.34 \rfloor = 6$.
Tarea moral
Los siguientes ejercicios son opcionales. Es decir, no formarán parte de tu calificación. Sin embargo, te recomiendo resolverlos para que desarrolles tu dominio de los conceptos abordados en esta entrada.
- Demuestra que si $X$ es una v.a., entonces se para cada $a \in \RR$ se cumple que\[ F_{X}(a-) = \Prob{X < a}. \]Sugerencia: Aplica el teorema de continuidad de la probabilidad a la sucesión de conjuntos $\{ A_{n} \}_{n\in\mathbb{N}^{+}}$, donde para cada $n\in\mathbb{N}^{+}$ definimos $A_{n} = (-\infty, a − \frac{1}{n}]$.
- Retomando el Ejemplo 1, encuentra la probabilidad de que «$X$ tome el valor $1$ o el valor $-1$».
- Encuentra la función de distribución de la variable aleatoria $Y$ del Ejemplo 2. Sugerencia: Nosotros obtuvimos $\Prob{Y \leq 5}$, ¿qué pasa si en vez de hacerlo para $5$, lo haces para cualquier $x \in \RR$?
Más adelante…
Más adelante veremos muchas v.a.’s discretas para las cuales $\mathbb{N}$ es un soporte. Como comentamos en la última sección de esta entrada, esto significará que el conjunto de valores que pueden tomar esas v.a.’s es $\mathbb{N}$ o algún subconjunto de $\mathbb{N}$. Por ello, la función de distribución de esas v.a.’s podrá escribirse utilizando la fórmula que obtuvimos en esa sección.
En la siguiente entrada abordaremos las v.a.’s continuas. Así como las v.a.’s discretas, las v.a.’s continuas tienen ciertas peculiaridades importantes que tenemos que analizar.
Entradas relacionadas
- Ir a Probabilidad I
- Entrada anterior del curso: Funciones de Distribución de Probabilidad
- Siguiente entrada del curso: Variables Aleatorias Continuas