Introducción
En la entrada anterior comenzamos el estudio de los dos tipos de v.a.’s que nos interesan, y vimos el caso de las v.a.’s discretas. Sin embargo, puede que te preguntes exactamente por qué es necesaria esta distinción. Por ello, en esta entrada presentaremos las propiedades de las v.a.’s continuas para que compares ambos tipos, y puedas apreciar sus diferencias.
A diferencia de las v.a.’s discretas, las v.a.’s continuas pueden tomar una cantidad infinita no numerable de valores distintos. Es decir, el conjunto de valores que puede tomar una v.a. continua tiene la misma cardinalidad que los números reales.
Definición de una v.a. continua
En la introducción comentamos que las v.a.’s continuas, a grandes rasgos, son aquellas cuyo conjunto de valores posibles es infinito no numerable. Sin embargo, no las definiremos a partir de este hecho, sino a partir de una propiedad que debe cumplir su función de distribución.
Definición. Una variable aleatoria $X$ es absolutamente continua si y sólamente si existe una función $f\colon\RR\to\RR$ integrable y no-negativa tal que para cada $x \in \RR$ se cumple que
\[ F_{X}(x) = \int_{-\infty}^{x} f(t) \text{d}t. \]
Llamamos a $f$ la función de densidad (o simplemente la densidad) de $X$.
A este tipo de v.a.’s se les llama absolutamente continuas debido a que su función de distribución es una función absolutamente continua. Es común encontrarse con el término «continua» en vez de «absolutamente continua«, aunque en contextos más formales existen diferencias entre ambos términos. De manera equivalente, una v.a. $X$ es continua si existe una función $f\colon\RR\to\RR$ integrable y no-negativa tal que para cada $x \in \RR$ se cumple que
\[ \Prob{X \leq x} = \int_{-\infty}^{x} f(t) \text{d}t, \]
por la definición de $F_{X}$. Es decir, $X$ es una v.a. continua si la función de distribución de $X$ puede escribirse como la integral de una función integrable y no-negativa $f$, que es llamada la densidad de $X$. Es decir, las probabilidades de los eventos que involucran a una v.a. continua se pueden expresar en términos del área debajo de su función de densidad.
En consecuencia, si $X$ es una v.a. continua con densidad $f\colon\RR\to\RR$, como $F_{X}(x) \to 1$ cuando $x \to \infty$, se tiene que
\[ \int_{-\infty}^{\infty} f(t)\text{d}t = 1. \]
Además, para cada $a$, $b \in \RR$ tales que $a < b$ se tiene que $\Prob{X \in (a, b]} = F_{X}(b) − F_{X}(a)$, por lo que
\[ \Prob{X \in (a, b]} = \int_{-\infty}^{b} f(t) \text{d}t − \int_{-\infty}^{a} f(t) \text{d}t = \int_{a}^{b} f(t) \text{d}t. \]
Es importante notar que en la definición pedimos que la densidad de una v.a. continua $X$ debe ser una función integrable, lo cual garantiza que la función de distribución de $X$ es continua.
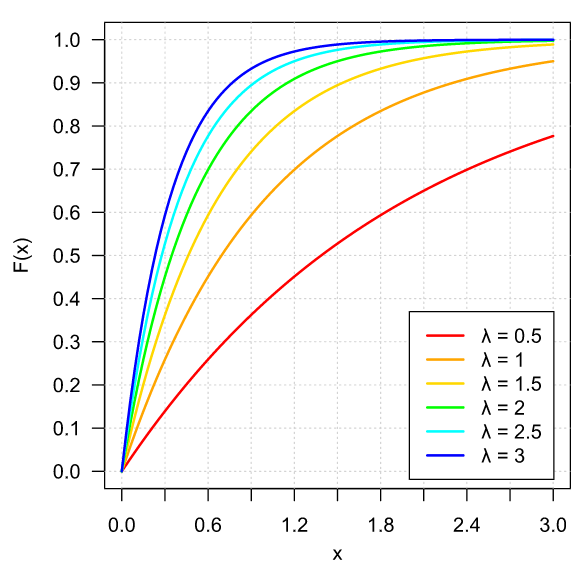
Ejemplo 1. Sea $\lambda \in \RR$ tal que $\lambda > 0$ y sea $X$ una v.a. con distribución $F\colon\RR\to\RR$ dada por
\[ F(x) = \begin{cases} 1 − e^{-\lambda x} & \text{si $x \geq 0$}, \\[1em] 0 & \text{en otro caso.} \end{cases} \]
Gráficamente, para algunos valores de $\lambda$, $F$ se ve como sigue:
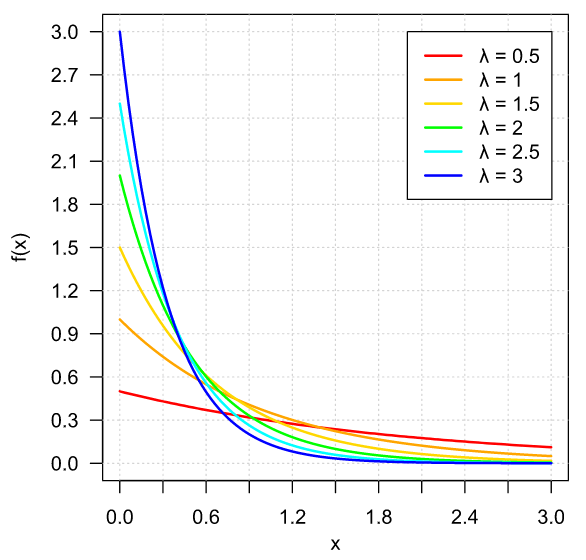
Si tomamos a $f\colon\RR\to\RR$ como sigue
\[ f(x) = \begin{cases} \lambda e^{-\lambda x} & \text{si $x \geq 0$}, \\[1em] 0 & \text{en otro caso,} \end{cases} \]
se cumplirá que $f$ es la densidad de $X$. Para verlo, tomamos $x \in \RR$. Primero, observa que si $x < 0$, entonces
\[ \int_{-\infty}^{x} f(t) \mathrm{d}t = \int_{-\infty}^{x} 0 \mathrm{d}t = 0 = F(x), \]
donde $F(x) = 0$ se cumple por la definición de $F$. Por otro lado, para el caso en el que $x \geq 0$ se tiene que
\begin{align*} \int_{-\infty}^{x} f(t) \mathrm{d}t &= \int_{-\infty}^{0} 0 \mathrm{d}t + \int_{0}^{x} \lambda e^{-\lambda t} \mathrm{d}t \\[1em] &= 0 + {\left( − e^{−\lambda t} \right)} \Big|_{0}^{x} \\[1em] &= e^{−\lambda \cdot 0} − e^{−\lambda x} \\[1em] &= 1 − e^{-\lambda x}, \end{align*}
por lo que queda demostrado que para cada $x \in \RR$ se cumple que $F(x) = \int_{−\infty}^{x} f(t) \mathrm{d}t$. Por lo tanto, $f$ es la densidad de $X$.
Cuando una v.a. tiene la función de distribución (y, en consecuencia, la densidad) del ejemplo anterior, se dice que sigue una distribución exponencial. Esta es una de las muchas distribuciones importantes que veremos más adelante.
¿Las v.a.’s continuas tienen función de masa de probabilidad?
Como seguramente ya notaste, la relación que existe entre la densidad y la función de distribución de una v.a. continua se parece mucho a la relación entre la masa de probabilidad y la distribución de una v.a. discreta. En el caso de las discretas, para obtener el valor de $F(x)$ para $x \in \RR$ a partir de la función de masa de probabilidad, lo que se hace es sumar todas las probabilidades de los valores menores o iguales a $x$. Por otro lado, en el caso de las continuas lo que se hace es integrar la función de densidad desde $−\infty$ hasta $x$.
Sin embargo, hay un detalle muy importante en el que difieren las v.a.’s continuas de las discretas, que desarrollaremos a continuación. Sea $X$ una v.a. continua. ¿Recuerdas la siguiente propiedad? La vimos en la entrada pasada. Para cada $a \in \RR$, se cumple que
\[ \Prob{X =a} = F_{X}(a) − F_{X}(a-), \]
donde no olvides que $F_{X}(a-)$ es el límite de $F(x)$ cuando $x$ tiende a $a$ por la izquierda. Sin embargo, en el caso de una v.a. continua, sabemos que existe $f\colon\RR\to\RR$ integrable y no-negativa tal que para cada $x \in \RR$, se cumple que
\[ F_{X}(x) = \int_{-\infty}^{x} f(t) \mathrm{d}t. \]
Debido a que $f$ es una función integrable, la función $F_{X}$ es continua. En particular, es continua por la izquierda, por lo que para cada $a \in \RR$ se cumple que
\[ \Prob{X = a} = F_{X}(a) − F_{X}(a-) = F_{X}(a) − F_{X}(a) = 0. \]
Esto seguramente te resulta confuso, ¿la probabilidad de que la v.a. $X$ tome cualquier valor real es $0$? ¡Así es! Sin embargo, nosotros habíamos dicho que en la probabilidad, medíamos qué tan «probable» es que pase un evento con una calificación del $0$ al $1$. En particular, habíamos acordado que $0$ representa lo más improbable posible. ¿Esto significa que es imposible que una v.a. continua tome algún valor fijo? ¡No! Ten mucho cuidado, nosotros dijimos que cuando un evento tiene probabilidad $0$ esto significa que es lo más improbable posible de acuerdo con la medida de probabilidad que se está utilizando. Esto puede interpretarse como que sí es imposible (como pasa con los puntos de probabilidad $0$ en una v.a. discreta, o los puntos donde la densidad de una v.a. continua vale $0$), o puede significar que es muy improbable, pero no imposible.
Además, debido a esto último, cuando $X$ es una v.a. continua se cumple que
\[ \Prob{X \in (a,b]} = \Prob{X \in (a,b)} = \Prob{X \in [a,b)} = \Prob{X \in [a,b]}, \]
y que
\[ \Prob{X \leq a} = \Prob{X < a}, \qquad \Prob{X \geq a} = \Prob{X > a}, \]
por lo que con las v.a.’s continuas no es necesario preguntarse si la desigualdad es estricta o no. Mucho cuidado, con las discretas sí debes de tener cuidado con eso, porque en las discretas hay valores $a \in \RR$ para los cuales $\Prob{X = a} > 0$.
Pese a que la probabilidad de los eventos $(X = a)$ es $0$ para cada $a \in \RR$ cuando $X$ es una v.a. continua, la variable aleatoria sí puede tomar cualquiera de los valores en los que su función de densidad es mayor a $0$.
Partiendo de una función de densidad
En la entrada pasada vimos que puede definirse la distribución de una v.a. discreta a partir de una función de masa de probabilidad. De manera muy similar, puede definirse la distribución de una v.a. continua a partir de una función de densidad. Sin embargo, hay que establecer las propiedades que debe de satisfacer una función para poder uitlizarla como función de densidad.
Sea $f\colon\RR\to\RR$ una función integrable. Si se cumple que
\begin{align*} f(x) \geq 0 &\quad \text{para cada $x \in \RR$,} \tag{1} \\[1em] \int_{−\infty}^{\infty} f(t) \mathrm{d}t &= 1, \tag{2}\end{align*}
entonces $f$ es la densidad de alguna v.a. continua. Para confirmar este hecho, define $F\colon\RR\to\RR$ como
\[ F(x) = \int_{−\infty}^{x} f(t) \mathrm{d}t, \quad \text{para cada $x \in \RR$,} \]
y demuestra (tarea moral) que $F$ es una función de distribución. Esto es, que $F$ es no-decreciente, continua por la derecha y su límite a $\infty$ es $1$ y a $−\infty$ es $0$.
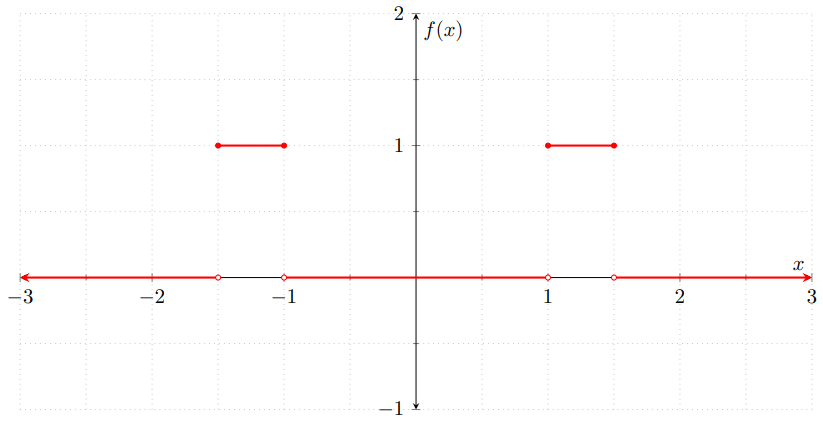
Ejemplo 2. La función de densidad de una v.a. continua debe de ser integrable. Sin embargo, no tiene por qué ser continua, ya que funciones integrables que tienen discontinuidades. Por ejemplo, considera a $f\colon\RR\to\RR$ dada por
\[ f(x) = \begin{cases} 1 & \text{si $x \in [−1.5, −1]$,} \\[1em] 1 & \text{si $x \in [1, 1.5]$,} \\[1em] 0 & \text{en otro caso.} \end{cases} \]
Gráficamente:
Para ver que $f$ es la función de densidad de alguna v.a. continua, hay que demostrar que $f$ satisface:
\begin{align*} f(x) \geq 0 \quad \text{para cada $x \in \RR$} \qquad \text{y} \qquad \int_{−\infty}^{\infty} f(t) \mathrm{d}t = 1.\end{align*}
Primero, observa que por la definición de $f$, para cada $x \in \RR$ se cumple que $f(x) = 0$ o $f(x) = 1$, por lo que $f$ es no-negativa. Por otro lado, veamos cuánto vale la integral de $f$ sobre $\RR$.
\begin{align*} \int_{−\infty}^{\infty} f(t) \mathrm{d}t &= \int_{−\infty}^{−1.5} f(t) \mathrm{d}t + \int_{−1.5}^{−1} f(t) \mathrm{d}t + \int_{−1}^{1} f(t) \mathrm{d}t + \int_{1}^{1.5} f(t) \mathrm{d}t + \int_{1.5}^{\infty} f(t) \mathrm{d}t \\[1em] &= \int_{−\infty}^{−1.5} 0 \mathrm{d}t + \int_{−1.5}^{−1} 1 \mathrm{d}t + \int_{−1}^{1} 0 \mathrm{d}t + \int_{1}^{1.5} 1 \mathrm{d}t + \int_{1.5}^{\infty} 0 \mathrm{d}t \\[1em] &= \int_{−1.5}^{−1} 1 \mathrm{d}t + \int_{1}^{1.5} 1 \mathrm{d}t \\[1em] &= {\Big( t \, \Big|_{−1.5}^{−1} \Big)} + {\Big( t \, \Big|_{1}^{1.5} \Big)} \\[1em] &= (−1 − (−1.5)) + (1.5 − 1) \\[1em] &= (−1 + 1.5) + (1.5 − 1) \\[1em] &= 0.5 + 0.5 \\[1em] &= 1, \end{align*}
por lo que $\int_{−\infty}^{\infty} f(t) \mathrm{d}t = 1$, así que $f$ es la función de densidad de alguna v.a. continua.
A partir de $f$ podemos obtener la función de distribución que le corresponde, donde para cada $x \in \RR$, se define $F$ como
\[ F(x) = \int_{-\infty}^{x} f(t) \mathrm{d}t. \]
Sin embargo, como $f$ está definida por pedazos, hay que tener cuidado con cada uno de los casos para $x$. En este caso, $f$ tiene $5$ casos que analizar. Primero, cuando $x < -1.5$, tenemos que
\[ F(x) = \int_{-\infty}^{x} f(t) \mathrm{d}t = \int_{-\infty}^{x} 0 \mathrm{d}t = 0, \]
pues $f(x) = 0$ cuando $x < -1.5$. Luego, cuando $-1.5 \leq x \leq 1$, tenemos que
\[ F(x) = \int_{-\infty}^{x} f(t) \mathrm{d}t = \int_{-\infty}^{-1.5} 0 \mathrm{d}t + \int_{-1.5}^{x} 1 \mathrm{d}t = 0 + {\Big( t \, \Big|_{-1.5}^{x} \Big)} = x − (-1.5) = x + 1.5, \]
¡observa con cuidado cómo los integrandos difieren debido a que $f$ está definida por pedazos! Continuando con el ejemplo, cuando $-1 < x < 1$, se tiene que
\begin{align*} F(x) = \int_{-\infty}^{x} f(t) \mathrm{d}t = \int_{-\infty}^{-1.5} 0 \mathrm{d}t + \int_{-1.5}^{-1} 1 \mathrm{d}t + \int_{-1}^{1} 0 \mathrm{d}t &= 0 + {\Big( t \, \Big|_{-1.5}^{-1} \Big)} + 0 \\[1em] &= (-1) − (-1.5) \\[1em] &= 0.5, \end{align*}
es decir, $F$ permanece constante entre $-1$ y $1$, y toma el valor $0.5$. Cuando $1 \leq x \leq 1.5$, la integral queda como sigue
\begin{align*} F(x) = \int_{-\infty}^{x} f(t) \mathrm{d}t &= \int_{-\infty}^{-1.5} 0 \mathrm{d}t + \int_{-1.5}^{-1} 1 \mathrm{d}t + \int_{-1}^{1} 0 \mathrm{d}t + \int_{-1}^{x} 1 \mathrm{d}t \\[1em] &= 0 + {\Big( t \, \Big|_{-1.5}^{-1} \Big)} + 0 + {\Big( t \, \Big|_{1}^{x} \Big)} \\[1em] &= ((-1) − (-1.5)) + (x − 1) \\[1em] &= 0.5 + x − 1 \\[1em] &= x − 0.5, \end{align*}
y así obtenemos la función de distribución asociada a $f$, que es
\[ F(x) = \begin{cases} 0 & \text{si $x < -1.5$}, \\[1em] x + 1.5 & \text{si $-1.5 \leq x \leq 1$}, \\[1em] 0.5 & \text{si $-1 < x < 1$}, \\[1em] x − 0.5 & \text{si $1 \leq x \leq 1.5$}, \\[1em] 1 & \text{si $1.5 \leq x$}, \end{cases} \]
que gráficamente se ve como la siguiente figura

Teniendo la función de distribución, es posible calcular muchas probabilidades. Si $U$ es una v.a. cuya distribución es la función $F$ que obtuvimos, entonces podemos obtener:
\[ \Prob{U \leq -\frac{4}{3}} = -\frac{4}{3} + 1.5 = -\frac{4}{3} + \frac{3}{2} = \frac{-8 + 9}{6} = \frac{1}{6} \approx 0.16666, \]
por lo que $\Prob{U \leq -\frac{4}{3}} \approx 16.666\%$. Además, como $U$ es una v.a. continua, se tiene que $\Prob{U \leq -\frac{4}{3}} = \Prob{U < -\frac{4}{3}}$, pues $\Prob{U = -\frac{4}{3}} = 0$. Esto pasa con cualquier valor, como ya mencionamos anteriormente. Por ello, al obtener probabilidades de que una v.a. continua esté dentro de algún intervalo, puedes no preocuparte por los extremos. Otro ejemplo:
\[ \Prob{X \in (-1.2, 1.4]} = F(1.4) − F(-1.2) = (1.4 − 0.5) − ((-1.2) + 1.5) = 0.9 − 0.3 = 0.6, \]
que es igual a $\Prob{X \in (-1.2, 1.4)}$, pues $\Prob{X = 1.4} = 0$.
Recuperando la densidad a partir de la distribución
Habrá situaciones en las que tendremos la función de distribución de una v.a. continua, y necesitaremos su función de densidad. El siguiente ejemplo exhibe una metodología para obtener la densidad de una v.a. continua a partir de su función de distribución.
Ejemplo 3. Sea $Z$ una v.a. con distribución $G\colon\RR\to\RR$ dada por
\[ G(z) = \begin{cases} 0 & \text{si $x < 0$}, \\[1em] z^2 & \text{si $0 \leq z < \frac{1}{2}$}, \\[1em] 1 − \dfrac{3(1 − z)}{2} & \text{si $\frac{1}{2} \leq z < 1$}, \\[1em] 1 & \text{si $z \geq 1$},\end{cases} \]
que gráficamente se ve como sigue:

Ahora, para obtener la función de densidad de $Z$, digamos, $g$. Para hacerlo, hay que hacer el procedimiento inverso al que seguimos en el ejemplo anterior. No obstante, la densidad $g$ será una función definida por pedazos, así como $G$ (y como la densidad del ejemplo anterior).
Además, en lugar de integrar, ahora tenemos que encontrar la derivada $G$. Es decir, la función $g$ que buscamos debe de satisfacer que
\[ G'(z) = g(z), \qquad \text{para cada $z\in\RR$.} \]
Sin embargo, observa que la función no es diferenciable sobre todo su dominio. Gráficamente, tiene un piquito en $z=\frac{1}{2}$, que es un indicador de que la función no es diferenciable en ese punto. Lo mismo pasa en $z=1$.
Sin embargo, es posible obtener la derivada de la función $G$ en los pedazos en los que sí es diferenciable. Podemos trabajar de manera similar a como lo hicimos en el ejemplo anterior, analizando cada uno de los casos que contempla la regla de correspondencia de $G$. De este modo, sea $z < 0$. Queremos encontrar $g_{1}$, una función no-negativa, tal que
\[ G(z) = \int_{-\infty}^{z} g_{1}(t) \mathrm{d}t, \]
y como $z < 0$, $G(z) = 0$, por lo que buscamos $g_{1}$ tal que
\[ \int_{-\infty}^{z} g_{1}(t) \mathrm{d}t = 0, \]
que debe de ser una función constante para que se cumpla que $G'(t) = g_{1}(t)$ para $t < 0$. Además, $g_{1}$ debe de ser no-negativa, pues buscamos que sea parte de una función de densidad, la cual debe de ser no negativa. De este modo, la única función $g_{1}$ que satisface este hecho es la función dada por $g_{1}(t) = 0$, pues es constante y su integral de $-\infty$ a $z$ es $0$, con $z < 0$. De este modo, $g$, la derivada de $G$ que buscamos, cumple que $g(z) = 0$ para cada $z < 0$.
Después, para $z \in [0, \frac{1}{2})$, tenemos que
\[ G(z) = z^{2}, \]
y lo que queremos es encontrar una función $g_{2}$ tal que
\[ G(z) = \int_{-\infty}^{0} g_{1}(t) \mathrm{d}t + \int_{0}^{z} g_{2}(t) \mathrm{d}t, \]
donde $g_{1}$ es la que obtuvimos en el paso anterior (gracias al paso anterior sabemos que la derivada de $G$ que estamos construyendo vale $0$ de $-\infty$ a $0$). Por ello, buscamos $g_{2}$ tal que
\[ z^{2} = \int_{-\infty}^{0} g_{1}(t) \mathrm{d}t + \int_{0}^{z} g_{2}(t) \mathrm{d}t = 0 + \int_{0}^{z} g_{2}(t) \mathrm{d}t = \int_{0}^{z} g_{2}(t) \mathrm{d}t, \]
por lo que $g_{2}$ es la función dada por $g_{2}(t) = 2z$ para cada $z \in [0, \frac{1}{2})$; ya que $\frac{\mathrm{d}}{\mathrm{d}z}{\left( z^{2} \right)} = 2z$.
Ahora, para $z \in [\frac{1}{2}, 1)$, se tiene que
\[ G(z) = 1 − \frac{3(1 − z)}{2}, \]
y ahora buscamos una función $g_{3}$ tal que
\[ G(z) = \int_{-\infty}^{0} g_{1}(t) \mathrm{d}t + \int_{0}^{\frac{1}{2}} g_{2}(t) \mathrm{d}t + \int_{\frac{1}{2}}^{z} g_{3}(t) \mathrm{d}t. \]
Desarrollando el lado derecho de esta última igualdad obtenemos la siguiente expresión
\begin{align*} \int_{-\infty}^{0} g_{1}(t) \mathrm{d}t + \int_{0}^{\frac{1}{2}} g_{2}(t) \mathrm{d}t + \int_{\frac{1}{2}}^{z} g_{3}(t) \mathrm{d}t &= 0 + {\left({\left( \frac{1}{2} \right)}^{2} − 0^{2} \right)} + \int_{\frac{1}{2}}^{z}g_{3}(t) \mathrm{d}t \\[1em] &= \frac{1}{4} + \int_{\frac{1}{2}}^{z}g_{3}(t) \mathrm{d}t, \end{align*}
y, por otro lado, desarrollando el lado izquierdo, obtenemos que
\[ G(z) = 1 − \frac{3(1 − z)}{2} = 1 − \frac{3 − 3z}{2} = \frac{2 − (3 − 3z)}{2} = \frac{3z − 1}{2} \]
por lo que la función $g_{3}$ que buscamos debe de cumplir que
\[ \frac{3z − 1}{2} = \frac{1}{4} + \int_{\frac{1}{2}}^{z}g_{3}(t) \mathrm{d}t, \]
que desarrollando un poco, nos dice que $g_{3}$ debe de satisfascer
\[ \frac{3z}{2} − \frac{3}{4} = \int_{\frac{1}{2}}^{z}g_{3}(t) \mathrm{d}t. \]
Ahora, esto es algo que no se notó mucho en el paso anterior en el que obtuvimos $g_{2}$, pero la expresión de la izquierda incluye las constantes de integración. Esto es de esperarse, pues se trata del teorema fundamental del cálculo.
Bien, ahora observa $\frac{\mathrm{d}}{\mathrm{d}z}{\left( \frac{3z}{2} − \frac{3}{4} \right)} = \frac{3}{2}$; así que $g_{3}(t) = \frac{3}{2}$ es la función que queremos. Más aún, podemos confirmarlo integrando $g_{3}$ de $\frac{1}{2}$ a $z$:
\[ \int_{\frac{1}{2}}^{z} \frac{3}{2} \mathrm{d}t = \frac{3}{2} \int_{\frac{1}{2}}^{z} 1 \mathrm{d}t = \frac{3}{2}{\left( z − \frac{1}{2} \right)} = \frac{3z}{2} − \frac{3}{4}, \]
por lo que $g_{3}(t) = \frac{3}{2}$ es precisamente la función que buscamos.
Finalmente, para $z \geq 1$, tenemos que $G(z) = 1$, por lo que nos queda encontrar $g_{4}$ tal que
\begin{align*} 1 &= \int_{-\infty}^{0} g_{1}(t) \mathrm{d}t + \int_{0}^{\frac{1}{2}} g_{2}(t) \mathrm{d}t + \int_{\frac{1}{2}}^{1} g_{3}(t) \mathrm{d}t + \int_{1}^{\infty} g_{4}(t) \mathrm{d}t, \\[1em] &= \int_{-\infty}^{0} 0 \mathrm{d}t + \int_{0}^{\frac{1}{2}} 2t \mathrm{d}t \mathrm{d}t + \int_{\frac{1}{2}}^{1} \frac{3}{2} \mathrm{d}t + \int_{1}^{\infty} g_{4}(t) \mathrm{d}t \\[1em] &= 0 + \frac{1}{4} + {\left( \frac{3}{2} − \frac{3}{4} \right) } + \int_{1}^{\infty} g_{4}(t) \mathrm{d}t \\[1em] &= \frac{1}{4} + {\left( \frac{6 − 3}{4} \right) } + \int_{1}^{\infty} g_{4}(t) \mathrm{d}t \\[1em] &= \frac{1}{4} + \frac{3}{4} + \int_{1}^{\infty} g_{4}(t) \mathrm{d}t \\[1em] &= 1 + \int_{1}^{\infty} g_{4}(t) \mathrm{d}t \end{align*}
por lo que $g_{4}$ debe de satisfacer que
\[ 1 = 1 + \int_{1}^{\infty} g_{4}(t) \mathrm{d}t, \]
o equivalentemente, que $\int_{1}^{\infty} g_{4}(t) \mathrm{d}t = 0$. Similarmente a $g_{1}$, la única función no-negativa que satisface esto es $g_{4}(z) = 0$, para cada $z \geq 1$. Así, colocando cada una de las funciones que hemos obtenido en el caso que le corresponde, obtenemos que la densidad de $Z$ es la función $g\colon\RR\to\RR$ dada por
\[ g(z) = \begin{cases} 0 & \text{si $x < 0$}, \\[1em] 2z & \text{si $0 \leq z < \frac{1}{2}$}, \\[1em] \frac{3}{2} & \text{si $\frac{1}{2} \leq z < 1$}, \\[1em] 0 & \text{si $z \geq 1$},\end{cases} \]
que gráficamente se ve como sigue:
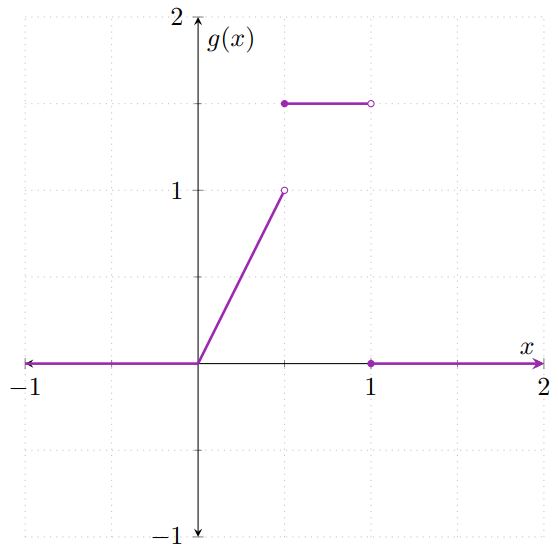
Usos de las variables aleatorias continuas
Las v.a.’s continuas tienen una cantidad no-numerable de valores que pueden tomar. Esto se debe a que $\RR$ y muchos de sus subconjuntos son ejemplos de conjuntos infinitos no-numerables. Por ejemplo, los intervalos $[0,1]$, $[0, \infty)$, $(−5, 3]$ son ejemplos de conjuntos con cardinalidad infinita no-numerable. Por ello, las v.a.’s continuas se utilizan en fenómenos cuyo resultado amerita usar la precisión de los números reales.
Un primer ejemplo son los fenómenos en donde el resultado es un valor de tiempo. El tiempo que esperas hasta que llega un autobús a la parada en la que lo tomas; el tiempo que tarda en fallar algún aparato electrónico (el ejemplo clásico es el tiempo que tarda un foco en fundirse); el tiempo de vida que le queda a una persona (espeluznante, pero a los actuarios les interesa debido a los seguros de vida); etcétera. Cuando se habla de tiempos, suelen usarse v.a.’s continuas que tengan a $[0, \infty)$ como soporte para asegurar que el modelo contempla únicamente valores no-negativos. Las v.a.’s con distribución exponencial (que mencionamos en el primer ejemplo de esta entrada) son un ejemplo de este tipo de v.a.’s.
Otro ejemplo donde se usan v.a.’s continuas son los fenómenos financieros. El precio de un activo en un momento dado; la paridad cambiaria entre divisas; el valor que tomará la tasa de interés o de rendimiento en un instrumento financiero (como una anualidad) en el futuro; etcétera. La teoría de los procesos estocásticos es la rama de la probabilidad que se encarga del estudio de fenómenos aleatorios a través del tiempo, y resulta fundamental para el análisis de fenómenos financieros como los que aquí mencionamos.
Tarea moral
Los siguientes ejercicios son opcionales. Es decir, no formarán parte de tu calificación. Sin embargo, te recomiendo resolverlos para que desarrolles tu dominio de los conceptos abordados en esta entrada.
- Demuestra que si $f\colon\RR\to\RR$ es una función que satisface \begin{align*} f(x) \geq 0 \quad \text{para cada $x \in \RR$} \qquad \text{y} \qquad \int_{−\infty}^{\infty} f(t) \mathrm{d}t = 1,\end{align*}entonces $f$ es la función de densidad de alguna v.a. continua. Sugerencia: Define $F\colon\RR\to\RR$ como sigue: para cada $x \in \RR$, \[ F(x) = \int_{−\infty}^{\infty} f(t) \mathrm{d}t, \]y demuestra que $F$ es una función de distribución.
- Demuestra que la función $g\colon\RR\to\RR$ dada por\[ g(x) = \begin{cases} x + 1 & \text{si $x \in [−1,0)$,} \\[1em] 1 − x & \text{si $x \in [0, 1]$,} \\[1em] 0 & \text{en otro caso} \end{cases} \]es la función de densidad de alguna v.a. continua. La gráfica de $g$ puede apreciarse en la siguiente figura:
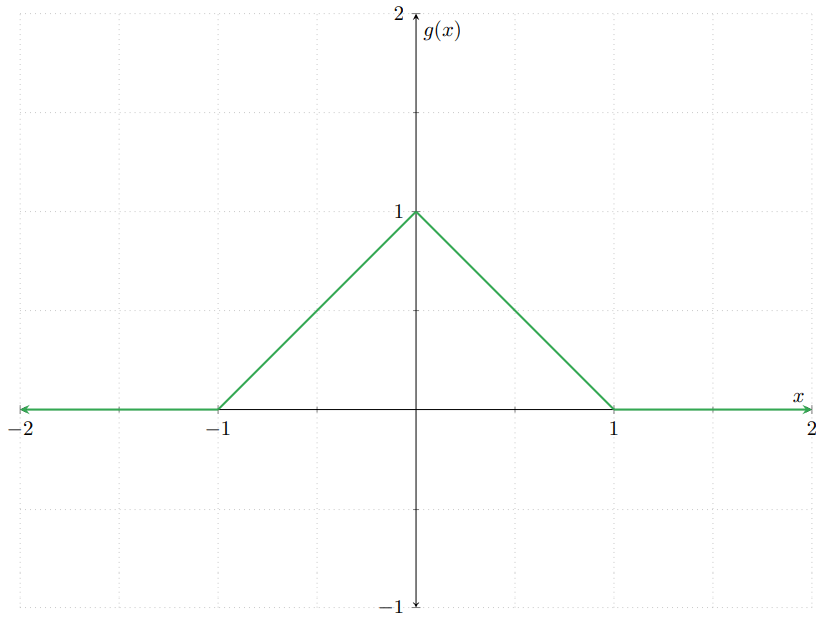
- Verifica que la función $G$ del Ejemplo 3 es una función de distribución.
Más adelante…
Es importante que entiendas las diferencias que existen entre las v.a.’s discretas y las continuas. Repasa esta entrada y la anterior las veces que sea necesario para que no te confundas entre ambas. En la siguiente entrada veremos qué es lo que resulta de aplicarle funciones (transformaciones) a una v.a.
En cuanto a las aplicaciones, verás muchísimas más en materias posteriores, como en las materias de estadística. Por nuestro lado veremos varias distribuciones de probabilidad importantes (como la distribución exponencial) con las que seguramente te encontrarás en ese tipo de materias.
Entradas relacionadas
- Ir a Probabilidad I
- Entrada anterior del curso: Variables Aleatorias Discretas
- Siguiente entrada del curso: Variables Aleatorias Mixtas