Introducción

Bienvenidos a la última unidad del curso de Ecuaciones Diferenciales Ordinarias. En la unidad anterior estudiamos sistemas de ecuaciones diferenciales de primer orden de la forma $$\begin{alignedat}{4} \dot{x}_{1} &= F_{1}(t,x_{1},x_{2},…,x_{n}) \\ \dot{x}_{2} &= F_{2}(t,x_{1},x_{2},…,x_{n}) \\ & \; \; \vdots \notag \\ \dot{x}_{n} &= F_{n}(t,x_{1},x_{2},…,x_{n}) \end{alignedat}.$$ En particular, estudiamos a profundidad sistemas de ecuaciones lineales de primer orden con coeficientes constantes, los cuales se pueden escribir de forma abreviada como $$\dot{\textbf{X}}=\textbf{A}\textbf{X}$$ donde $\textbf{A}$ es una matriz cuadrada cuyas entradas son los coeficientes del sistema. Mediante el método de valores y vectores propios logramos hallar la solución general a tales sistemas dependiendo de la forma de la matriz $\textbf{A}$ y sus valores propios.

En esta unidad continuaremos estudiando sistemas de ecuaciones y sus soluciones pero desde un punto de vista cualitativo. En particular, nos enfocaremos en sistemas de dos ecuaciones de primer orden y en su plano fase, el cual es un dibujo que nos da la información suficiente para saber cómo se comportan las soluciones. Nos limitaremos inicialmente a estudiar ecuaciones lineales con coeficientes constantes, pero en próximas entradas analizaremos sistemas no lineales, los cuales no hemos resuelto de manera analítica (los métodos son complejos para abordar en un primer curso), pero podremos estudiarlos cualitativamente.

Comenzaremos en esta entrada definiendo el plano fase y el campo vectorial asociado al sistema, el cual nos ayudará a dibujar las curvas que representan a las soluciones del sistema, y veremos algunos ejemplos que nos ayudarán a entender tales conceptos.

¡Vamos a comenzar!

Plano fase de un sistema de dos ecuaciones de primer orden

Definimos el concepto de sistema de ecuaciones autónomo (cuyas ecuaciones no dependen explícitamente de la variable independiente $t$), asociamos a cada solución del sistema una curva en el plano $x(t) – y(t)$, y definimos el plano fase asociado al sistema.

Campo vectorial asociado al sistema

Definimos el campo vectorial asociado a un sistema de dos ecuaciones y estudiamos la relación que guarda con las curvas del plano fase del sistema.

Tarea moral

Los siguientes ejercicios no forman parte de la evaluación del curso, pero te servirán para entender mucho mejor los conceptos vistos en esta entrada, así como temas posteriores.

Los campos vectoriales de las imágenes fueron realizados en el siguiente enlace.

• Encuentra la solución general al sistema $$\dot{\textbf{X}}=\begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix}\textbf{X}.$$ ¿Cuál es el campo vectorial asociado al sistema? Dibuja a mano algunos vectores del campo vectorial, y algunas curvas solución en el plano fase. ¿Puedes dibujarlas todas con la información obtenida?

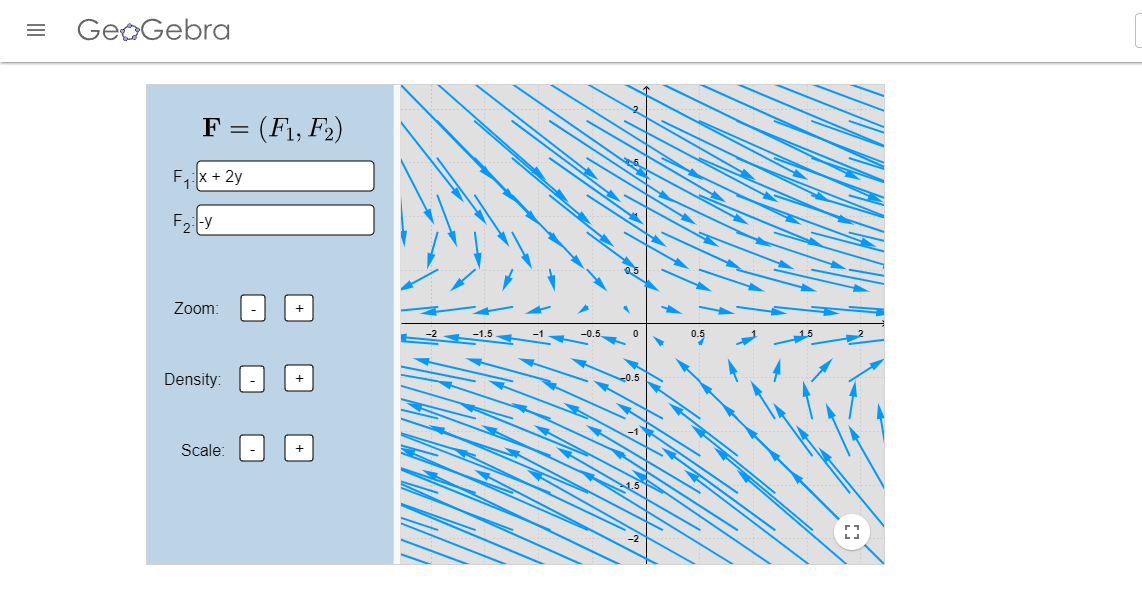
• Encuentra la solución general al sistema $$\dot{\textbf{X}}=\begin{pmatrix} 1 & 2 \\ 0 & -1 \end{pmatrix}\textbf{X}.$$ Dibuja algunas curvas solución en el plano fase. En la siguiente imagen puedes ver el campo vectorial asociado.

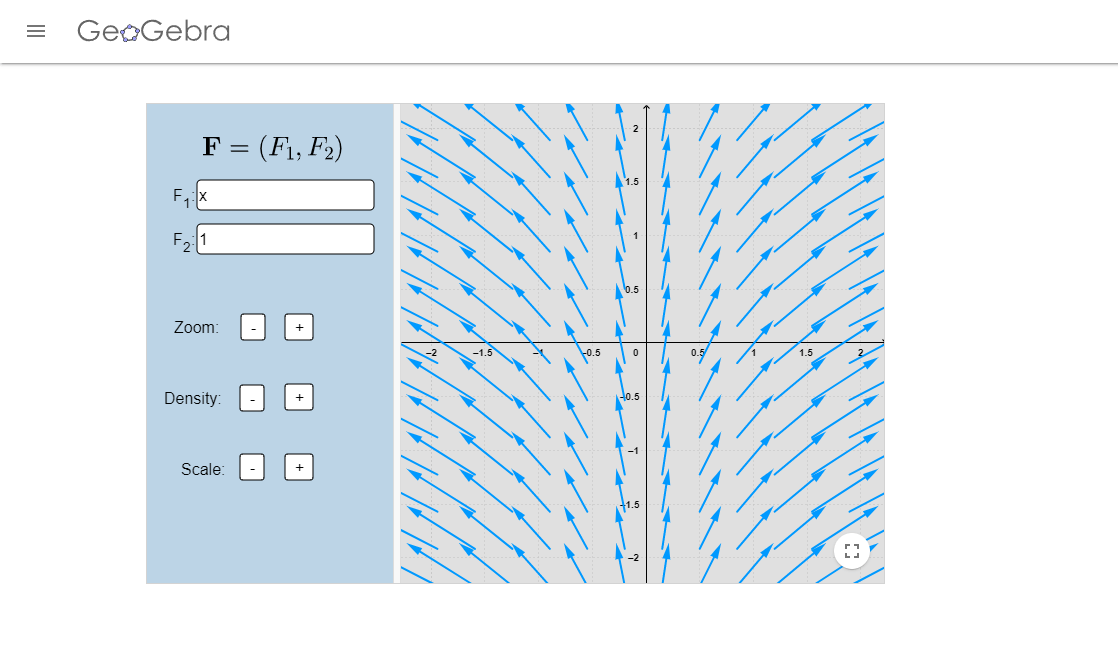
• Resuelve el sistema $$\dot{\textbf{X}}=\begin{pmatrix} 1 & 0 \\ 0 & 0 \end{pmatrix}\textbf{X}+\begin{pmatrix} 0 \\ 1\end{pmatrix}.$$ Dibuja algunas curvas solución en el plano fase. En la siguiente imagen puedes ver el campo vectorial asociado.

• En el primer video vimos que cada solución a un sistema $\dot{\textbf{X}}=\textbf{A}\textbf{X}$ determina una curva en el plano fase. Considera ahora una curva solución en el plano fase. ¿Determina una única solución al sistema? Es decir, ¿esta curva representa a una única solución al sistema?

• Considera el sistema $$\dot{\textbf{X}}=\begin{pmatrix} 1 & 2 \\ -2 & 1 \end{pmatrix}\textbf{X}.$$ Determina si el siguiente dibujo puede representar al campo vectorial asociado.

Más adelante

Una vez que hemos definido el plano fase de un sistema de dos ecuaciones $\dot{\textbf{X}}=\textbf{F}(x,y)$, vamos a comenzar a estudiar el comportamiento de las curvas solución. Para esto debemos estudiar los puntos de equilibrio, que serán aquellos puntos $(x,y)$ tales que $\textbf{F}(x,y)=(0,0)$. De dichos puntos va a depender el comportamiento del plano fase entero, por lo que estudiaremos su estabilidad.

Entradas relacionadas

• Ir a Ecuaciones Diferenciales I
• Entrada anterior del curso: Teorema de existencia y unicidad para sistemas de ecuaciones de primer orden
• Siguiente entrada del curso: Puntos de equilibrio y estabilidad para sistemas de dos ecuaciones de primer orden

• Notas escritas relacionadas con el tema: Introducción a la teoría cualitativa de las ecuaciones diferenciales
• Notas escritas relacionadas con el tema: Propiedades cualitativas de las trayectorias

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»