¿Cómo es posible un error en las matemáticas?.
– Henri Poincare
Introducción
Continuando con la descripción cualitativa de las ecuaciones diferenciales, en esta entrada estudiaremos las ecuaciones diferenciales en las que la función razón no depende explícitamente de la variable independiente $x$.
En la entrada anterior vimos una propiedad geométrica interesante de las ecuaciones diferenciales de la forma
$$\dfrac{dy}{dx} = f(y) \label{1} \tag{1}$$
dicha propiedad es que los elementos lineales en dos puntos distintos del plano $XY$, pero con la misma coordenada $y$, tienen la misma pendiente, esta propiedad tiene interesantes consecuencias y las estudiaremos en esta entrada.
Ecuaciones de primer orden autónomas
$$F(y, y^{\prime}) = 0 \label{2} \tag{2}$$ se llama autónoma.
Una ecuación autónoma en su forma normal se ve como (\ref{1}).
La ecuación diferencial
$$\dfrac{dy}{dx} = 1 + 2y$$
es una ecuación diferencial autónoma, mientras que la ecuación
$$\dfrac{dy}{dx} = 2xy$$
es una ecuación no autónoma ya que la función razón
$$f(x, y) = 2xy$$
sí depende de la variable independiente $x$.
Hay muchos procesos físicos que son modelados con ecuaciones diferenciales autónomas donde la variable independiente puede ser por ejemplo el tiempo $t$, en estos casos dichos procesos no cambiarían en el tiempo.
Puntos críticos
En la ecuación diferencial autónoma (\ref{1}) las raíces de la función razón son de especial importancia.
Un punto crítico también es llamado punto de equilibrio o punto estacionario.
Con estas dos definiciones podemos observar que si $k$ es un punto crítico de la ecuación (\ref{1}), entonces $y(x) = k$ es una solución constante de la ecuación diferencial autónoma.
Esquema de fases
En la entrada anterior vimos que una propiedad geométrica de las ecuaciones autónomas es que los elementos lineales son paralelos a lo largo de líneas horizontales en el plano $XY$, esto quiere decir que si conocemos el campo de pendientes a lo largo de una sola línea vertical $x = x_{0}$, entonces lo conocemos para todo el plano $XY$. Esta propiedad nos permite, en lugar de dibujar todo el plano, dibujar una sola línea que contiene la misma información. Esta línea se llama línea fase para la ecuación autónoma.
Para ver cómo obtener los puntos críticos, soluciones de equilibrio y líneas fase realicemos el siguiente ejemplo con una ecuación logística.
Ejemplo: Obtener los puntos críticos, soluciones de equilibrio y línea fase de la siguiente ecuación diferencial autónoma.
$$\dfrac{dy}{dx} = y(\alpha -\beta y) \label{3} \tag{3}$$
con $\alpha$ y $\beta$ constantes positivas.
Solución: Para obtener las soluciones de equilibrio y los puntos críticos igualamos la función razón a cero.
$$f(y) = y(\alpha -\beta y) = 0$$
La ecuación se satisface si $y = 0$ o $\alpha -\beta y = 0$, es decir, si
$$y(x) = 0 \hspace{1cm} o \hspace{1cm} y(x) = \dfrac{\alpha}{\beta}$$
Estas funciones corresponden a las soluciones de equilibrio de la ecuación diferencial y los puntos críticos no son más que las constantes $k_{1} = 0$ y $k_{2} = \dfrac{\alpha}{\beta} > 0$.
Para esbozar la línea fase comencemos por colocar dos puntos sobre una línea vertical, dichos puntos corresponden a los puntos críticos obtenidos.
La línea fase es paralela al eje $Y$, o bien puede ser el mismo eje $Y$.
En este caso los puntos críticos dividen a la línea fase en tres intervalos:
$$(-\infty, 0), \hspace{1cm} \left( 0, \dfrac{\alpha}{\beta} \right) \hspace{1cm} y \hspace{1cm} \left(\dfrac{\alpha}{\beta}, \infty\right)$$
Por definición los puntos críticos son los valores en los que
$$\dfrac{dy}{dx} = f(k) = 0$$
esto significa que la pendiente de los elementos lineales en los puntos críticos debe ser cero, mientras que por encima y por debajo de los puntos críticos la pendiente tiene que ser distinta de cero, así que puede haber elementos lineales con pendiente negativa o pendiente positiva.
Veamos en cada uno de los intervalos de nuestro ejemplo que signo tiene la pendiente de los elementos lineales, como se trata de un diagrama unidimensional dicho valor lo representaremos con flechas sobre la línea fase, si la pendiente es positiva colocaremos una flecha apuntando hacia arriba y si es una pendiente negativa colocaremos una flecha apuntando hacia abajo.
Para ver si la pendiente es positiva o negativa estudiemos el signo de la función razón (que es equivalente al signo de la derivada $\dfrac{dy}{dx}$) en cada uno de los intervalos. Comencemos con el intervalo $(-\infty, 0)$, en este caso $-\infty < y < 0$.
\begin{align*}
y &< 0 \\
\beta y &< 0 \\
-\beta y &> 0 \\
-\beta y + \alpha > \alpha &> 0 \\
f(y) = y(\alpha -\beta y) &< 0 \\
\dfrac{dy}{dx} &< 0
\end{align*}
Este análisis nos indica que la pendiente de los elementos lineales en el intervalo $(-\infty, 0)$ es negativa.
Haciendo un análisis similar en los intervalos $\left( 0, \dfrac{\alpha}{\beta} \right)$ y $\left(\dfrac{\alpha}{\beta}, \infty \right)$ obtenemos los siguientes resultados:
- En $(-\infty, 0)$ $\hspace{0.2cm}$ $\Rightarrow$ $f(y) = y(\alpha -\beta y) < 0$ $\Rightarrow$ La pendiente es negativa
- En $\left( 0, \dfrac{\alpha}{\beta} \right)$ $\hspace{0.2cm}$ $\Rightarrow$ $f(y) = y(\alpha -\beta y) > 0$ $\Rightarrow$ La pendiente es positiva.
- En $\left( \dfrac{\alpha}{\beta}, \infty \right)$ $\hspace{0.05cm}$ $\Rightarrow$ $f(y) = y(\alpha -\beta y) < 0$ $\Rightarrow$ La pendiente es negativa.
Como mencionamos antes, en el intervalo $(-\infty, 0)$ de la línea fase colocaremos una flecha apuntando hacia abajo debido a que la pendiente es negativa. En el intervalo $\left( 0, \dfrac{\alpha}{\beta} \right)$ colocaremos una flecha apuntando hacia arriba ya que la pendiente es positiva y finalmente en el intervalo $\left(\dfrac{\alpha}{\beta}, \infty \right)$ colocaremos nuevamente una flecha hacia abajo debido a que la pendiente vuelve a ser negativa. La línea fase de la ecuación diferencial dada se muestra en la siguiente figura.
Como caso particular consideremos la ecuación diferencial autónoma
$$\dfrac{dy}{dx} = y(6 -3y)$$
Las soluciones de equilibrio son $y(x) = 0$ y $y(x) = \dfrac{\alpha}{\beta} = \dfrac{6}{3} = 2$. A continuación se muestra el campo de pendientes de esta ecuación.
Notamos que, en efecto, el valor de la pendiente de los elementos lineales en las soluciones de equilibrio es cero, por encima de $y(x) = 2$ y por debajo de $y(x) = 0$ la pendiente es negativa y entre las soluciones de equilibrio la pendiente de los elementos lineales es positiva, tal como lo mostramos en la línea fase del caso general.
$\square$
Como podemos ver, la línea fase es una gran herramienta que nos permite analizar el comportamiento de las soluciones de una ecuación diferencial autónoma gracias a que las pendientes de los elementos lineales en líneas horizontales del plano $XY$ son siempre iguales.
Con el ejemplo en mente ahora podemos establecer los pasos necesarios para dibujar una línea fase de una ecuación diferencial autónoma.
- Comenzamos por dibujar una línea vertical paralela al eje $Y$ para cualquier valor de $x$.
- Determinamos las soluciones de equilibrio y los puntos críticos, marcamos los puntos críticos sobre la línea vertical.
- Determinamos los intervalos de $y$ en los que $f(y) > 0$ y dibujamos flechas apuntando hacia arriba en esos intervalos.
- Determinamos los intervalos de $y$ en los que $f(y) < 0$ y dibujamos flechas apuntando hacia abajo en esos intervalos.
Las líneas fase nos permiten obtener una aproximación cualitativa de las curvas solución de una ecuación diferencial autónoma.
Nota: En ocasiones se usan de forma indistinta los términos puntos críticos y soluciones de equilibrio, sin embargo podemos pensar a un punto crítico como el punto $c = k$ que se coloca en la línea fase, mientras que una solución de equilibrio $y(x) = k$ como la gráfica en el plano $XY$ de una función constante para toda $x$. Cuando estamos analizando líneas fase puede ser que al punto crítico también se le llame solución de equilibrio y es correcto debido a que la línea fase representa al eje de la variable dependiente $y$ para cualquier valor de la variable independiente $x$. Lo importante es que tengamos presente las definiciones de punto crítico y de solución de equilibrio que establecimos al inicio para evitar confusiones.
Ahora veamos que nos dice esta descripción cualitativa acerca de la forma de una curva solución de una ecuación diferencial autónoma.
Curvas solución de una ecuación diferencial autónoma
En la ecuación diferencial autónoma (\ref{1}) la función $f$ es independiente de la variable $x$, esto nos permite suponer que $f$ está definida en $x \in (-\infty, \infty)$, o en $x \in [0, \infty)$. Consideremos una región $U$ en el plano $XY$ en el que se cumple el teorema de existencia y unicidad de una solución, por este teorema sabemos que existe una solución que pasa por el punto $(x_{0}, y_{0})$. En la región $U$ supongamos que una ecuación diferencial autónoma tiene dos puntos críticos $c_{1}$ y $c_{2}$ tales que $c_{1} < c_{2}$. Las gráficas de las soluciones
$$y(x) = c_{1} \hspace{1cm } y \hspace{1cm} y(x) = c_{2}$$
son rectas horizontales que dividen a la región $U$ en tres regiones: $U_{1}, U_{2}$ y $U_{3}$, esto se puede visualizar en la siguiente figura.
Con estas condiciones podemos establecer las siguientes propiedades.
- Si el punto $(x_{0}, y_{0})$ está en alguna subregión $U_{i}$, $i = 1, 2, 3$ y $y(x)$ es una solución cuya curva solución pasa por $(x_{0}, y_{0})$, entonces $y(x)$ debe permanecer en esa subregión $U_{i}$ para toda $x$.
Esto indica que una solución $y(x)$ no puede cruzar la grafica de una solución de equilibrio $y(x) = c$. Para argumentar este hecho consideremos a $k$ como un punto crítico de una ecuación diferencial autónoma tal que $f(k) = 0$, considerando que $f(y)$ es continua, si las soluciones $y(x)$ son cercanas a $k$, entonces el valor de $f$ debe ser pequeño, esto nos indica que las soluciones se están desplazando lentamente cuando están próximas a los puntos críticos, dicho de otra manera, una solución que se acerca a un punto crítico cuando $x$ crece (o decrece) se mueve cada vez más lento al acercarse a éste. Por el teorema de existencia y unicidad, una solución que se acerca a un punto crítico nunca llega realmente a él, es decir, la solución de equilibrio se vuelve una asíntota para todas las soluciones $y(x)$ que se aproximan al punto crítico.
En la figura anterior, por ejemplo, la curva $y(x)$ que pasa por el punto $(x_{0}, y_{0})$ debe mantenerse dentro de $U_{2}$ para toda $x$, $y(x)$ está acotada por arriba con $c_{2}$ y por abajo con $c_{1}$, esto es, $c_{1} < y(x) < c_{2}$.
Otra propiedad es la siguiente.
- Por continuidad de la función $f$, debe ser $f(y) > 0$ o $f(y) < 0$ para toda $x$ en una subregión $U_{i}$, $i = 1, 2, 3$.
Vimos anteriormente que el signo de la pendiente se mantiene igual dentro de toda la región limitada por los puntos críticos, esto nos permite deducir que una curva solución $y(x)$ no puede oscilar o tener extremos relativos (máximos o mínimos) dentro de una misma región. Esto lo podemos describir con la siguiente propiedad.
- Debido a que $\dfrac{dy}{dx} = f(y(x))$ es positiva o negativa en una subregión $U_{i}$, $i = 1, 2, 3$, una solución $y(x)$ es estrictamente monótona, por lo tanto no puede oscilar ni tener extremos relativos.
Ahora que conocemos estas propiedades podemos establecer una más que se puede deducir de las anteriores. Basándonos en el caso general de la imagen anterior podemos decir lo siguiente.
- Si $y(x)$ es una solución dentro de la región $U_{1}$, entonces está acotada por arriba con el punto crítico $c_{1}$, esto es, $\forall$ $x$ en el intervalo $$y(x) < c_{1}$$ Esto indica que la curva solución $y(x)$ debe tender a la gráfica de la solución de equilibrio $y(x) = c_{1}$ a medida que $x \rightarrow \infty$ o $x \rightarrow -\infty$. Por otro lado, una solución $y(x)$ que este en la región $U_{2}$ está acotada por abajo con $c_{1}$ y arriba con $c_{2}$, esto es, $\forall$ $x$ en el intervalo $$c_{1} < y(x) < c_{2}$$ Entonces la curva solución $y(x)$ debe tender a las gráficas de las soluciones de equilibrio $y(x) = c_{1}$ y $y(x) = c_{2}$ conforme $x \rightarrow \infty$ en una y $x \rightarrow -\infty$ en la otra. Finalmente, si la solución está en la region $U_{3}$ entonces está acotada por abajo con $c_{2}$, es decir, $\forall$ $x$ $$y(x) > c_{2}$$ En este caso la grafica $y(x)$ debe tender a la gráfica de la solución de equilibrio $y(x) = c_{2}$ conforme $x \rightarrow \infty$ o $x \rightarrow -\infty$.
Veamos la importancia de estas propiedades en un ejemplo.
Modelo logístico de la población
En esta entrada ya estudiamos como ejemplo la ecuación logística (\ref{3}), usemos los resultados obtenidos para resolver de manera cualitativa el problema del modelo logístico de la población visto en la entrada anterior. El modelo que establecimos fue
$$\dfrac{dP}{dt} = k \left(1 -\dfrac{P}{N}\right) P \label{4} \tag{4}$$
Este modelo corresponde a una ecuación diferencial autónoma.
$$\dfrac{dP}{dt} = f(P) \label{5} \tag{5}$$
así que las curvas solución las podemos describir con la teoría que hemos construido en esta entrada.
El problema que analizábamos era el crecimiento de la población en función de su entorno y los recursos limitados a los que están sujetos. Resolvamos la ecuación diferencial de manera cualitativa aplicando lo que hemos aprendido hasta ahora e interpretemos los resultados.
Comencemos por determinar las soluciones de equilibrio y los puntos críticos, para ello igualemos la ecuación a cero.
$$\dfrac{dP}{dt} = k \left(1 -\dfrac{P}{N}\right) P = 0$$
Esta relación se satisface si
$$kP = 0 \hspace{1cm} o \hspace{1cm} 1 -\dfrac{P}{N} = 0$$
Es decir, si $P = 0$ o $P = N$. Por lo tanto, los puntos críticos son $c_{1} = 0$ y $c_{2} = N$, mientras que las soluciones de equilibrio son $P(t) = 0$ y $P(t) = N$.
Coloquemos los puntos críticos sobre la línea fase.
Los puntos críticos definen tres intervalos para $P$, estos son
$$(-\infty, 0), \hspace{1cm} (0, N) \hspace{1cm} y \hspace{1cm} (N, \infty)$$
Sin embargo, como se trata de un problema real es claro que no tiene sentido que la variable población $P(t)$ sea negativa (no hay individuos negativos), así mismo no hay tiempos negativos por lo que $t > 0$, por lo tanto en este problema sólo consideraremos los intervalos $(0, N)$ y $(N, \infty)$ para $P$, así como $0 < t < \infty$.
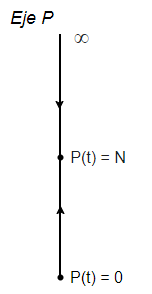
Del caso general (\ref{3}) deducimos que en el intervalo $(0, N)$ las pendientes son positivas, así que la función $P(t)$ será creciente en dicho intervalo y en $(N, \infty)$ las pendientes son negativas, por tanto la función $P(t)$ será decreciente. La línea fase final queda de la siguiente manera.
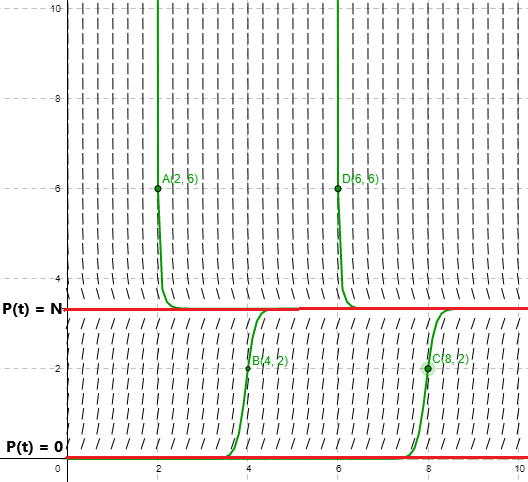
Un ejemplo de como se ve el campo de pendientes, las soluciones de equilibrio y algunas curvas solución de la ecuación logística (\ref{4}) se muestra en la siguiente figura.
De este gráfico notamos que las curvas solución cumplen con las hipótesis que establecimos al plantear el modelo, dichas hipótesis eran
- Si la población es pequeña $(P(t) < N)$, la tasa de crecimiento de la población es proporcional a su tamaño.
- Si la población es demasiado grande para ser soportada por su entorno y recursos $(P(t) > N)$, la población disminuirá, en este caso la tasa de crecimiento será negativa.
Las soluciones de equilibrio $P(t) = 0$ y $P(t) = N$ tienen sentido, pues si la población es cero permanecerá en cero indefinidamente y si la población es exactamente la asociada con la capacidad de soporte, entonces no crecerá ni disminuirá.
Es así que a partir de la línea fase y el campo de pendientes de una ecuación diferencial autónoma podemos esbozar varias curvas solución con distintas condiciones iniciales. En este ejemplo la única información que necesitamos es el hecho de que $P = 0$ y $P = N$ son soluciones de equilibrio, $P(t)$ crece si $0 < P < N$ y disminuye si $P > N$ o $P < 0$. Los valores exactos de $P(t)$ en cualquier tiempo dado $t$ dependerán de los valores $P(0)$, $k$ y $N$.
$\square$
Clasificación de puntos de equilibrio
Como vimos, alrededor de un punto crítico las soluciones pueden tener distintos comportamientos. Básicamente hay tres tipos de comportamiento que $y(x)$ puede tener alrededor de un punto crítico y en base a estos comportamientos podemos clasificarlos.
Supongamos que $y(x) = y_{0}$ es una solución de equilibrio de la ecuación diferencial autónoma (\ref{1}), los tres tipos de comportamiento que $y(x)$ puede tener alrededor del punto crítico $y_{0}$ son:
- Caso 1: Por arriba de $y_{0}$ la función $y(x)$ es decreciente y por debajo de $y_{0}$ la función $y(x)$ es creciente, en este caso decimos que el punto crítico es un atractor.
- Caso 2: Por arriba de $y_{0}$ la función $y(x)$ es creciente y por debajo de $y_{0}$ la función $y(x)$ es decreciente, en este caso decimos que el punto crítico es un repulsor.
- Caso 3: Tanto por arriba y por abajo de $y_{0}$ la función $y(x)$ es creciente o decreciente, en este caso decimos que el punto crítico es un nodo o punto semiestable.
En resumen, sea $y(x)$ solución de una ecuación diferencial autónoma (\ref{1}).
- Si $f(y_{0}) = 0$, entonces $y_{0}$ es un punto crítico y $y(x) = y_{0}$ es la solución de equilibrio para toda $x$.
- Si $f(y_{0}) > 0$, entonces $y(x)$ es creciente para toda $x$ y $y(x) \rightarrow \infty$, cuando $x$ incrementa, o bien $y(x)$ tiende al primer punto de equilibrio mayor que $y_{0}$.
- Si $f(y_{0}) < 0$, entonces $y(x)$ es decreciente para toda $x$ y $y(x) \rightarrow -\infty$, cuando $x$ incrementa, o bien $y(x)$ tiende al primer punto de equilibrio menor que $y_{0}$.
Importante mencionar que esto también es valido para $x$ negativas. Cuando $x$ decrece podemos encontrar resultados similares.
- Si $f(y_{0}) > 0$, entonces $y(x) \rightarrow -\infty$ o al siguiente punto de equilibrio menor conforme $x$ aumenta en valores negativos.
- Si $f(y_{0}) < 0$, entonces $y(x) \rightarrow \infty$ o al siguiente punto de equilibrio mayor conforme $x$ aumenta en valores negativos.
Un caso especial
Consideremos la ecuación diferencial autónoma
$$\dfrac{dy}{dx} = \dfrac{1}{1 -y}$$
Intentemos esbozar la línea fase. Por definición, los puntos críticos son los valores para los que $f(y) = 0$, sin embargo en este caso $f(y)$ no puede ser cero.
Notemos que si $y > 1$, entonces $f(y) < 0$ y si $y < 1$, entonces $f(y) > 0$, pero si $y = 1$, $f(y)$ no esta definida. En este caso decimos que la línea fase tiene un agujero en $y =1$ y lo denotamos como un circulo vacío.
Las soluciones $y(x)$ de la ecuación tienden hacia $y = 1$ cuando $x$ aumenta.
Concluyamos esta entrada con el enunciado de un teorema importante.
Teorema de linearización
Existe un teorema conocido como teorema de linearización que nos ayuda a determinar el tipo de puntos críticos de una ecuación diferencial autónoma (\ref{1}), de acuerdo al comportamiento que tiene la función $f(y)$. El enunciado de este teorema es el siguiente.
La demostración a este teorema la podemos encontrar en la sección de videos.
Tarea moral
Los siguientes ejercicios no forman parte de la evaluación del curso, pero servirán para entender mucho mejor los conceptos vistos en esta entrada, así como temas posteriores.
- Para las siguientes ecuaciones diferenciales, esbozar las líneas fase y clasificar a los puntos críticos como atractores, repulsores o nodos según sea el caso.
- $\dfrac{dy}{dx} = 3y(1 -y)$
- $\dfrac{dv}{du} = \dfrac{1}{v -2}$
- $\dfrac{dy}{dt} = \cos(y)$
- $\dfrac{dw}{dt} = w^{2} -6w -16$
- Para cada condición inicial dada, describir cualitativamente el comportamiento a largo plazo de las soluciones de la ecuación diferencial
$\dfrac{dy}{dx} = y^{2} -4y + 2$
con condición inicial
- $y(0) = 0$
- $y(0) = 10$
- $y(3) = 1$
Más adelante…
En estas dos últimas entradas hemos estudiado a las ecuaciones diferenciales ordinarias de primer orden desde una perspectiva cualitativa, esto nos ha permitido esbozar las curvas solución y encontrar propiedades interesantes sin siquiera conocer la forma explicita de la solución. En particular, las ecuaciones diferenciales autónomas presentan propiedades interesantes que son útiles para analizar modelos que describen algún fenómeno real.
Ha llegado el momento de estudiar los distintos métodos de resolución de las ecuaciones diferenciales ordinarias de primer orden. Comenzaremos con un método sencillo que funciona sólo para ecuaciones diferenciales lineales.
Entradas relacionadas
- Página principal del curso: Ecuaciones Diferenciales I
- Entrada anterior del curso: Campos de pendientes y su ecuación diferencial asociada
- Siguiente entrada del curso: Ecuaciones diferenciales lineales de primer orden – Método por factor integrante
- Video relacionado al tema: Ecuaciones autónomas, soluciones de equilibrio, línea fase y esbozo de soluciones
Agradecimientos
Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»




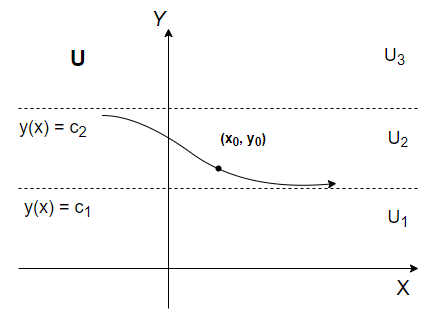
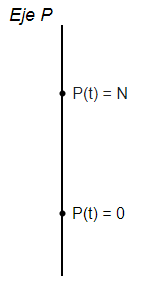
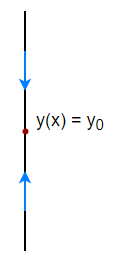
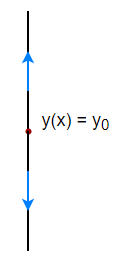
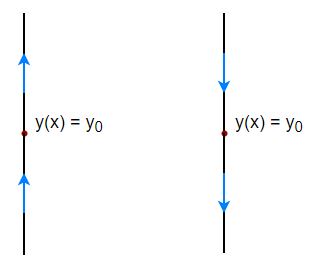
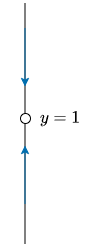
Me llama la atención, en ing.quimic a en los cursos de ec,difernciales no se ven estos temas .
Hola Omar. En efecto, en algunos cursos de otras licenciaturas sólo se discute de las ecuaciones diferenciales a veces muy superficialmente. Pero hay mucha teoría interesante alrededor de ellas, y a veces es bueno introducirse más en el tema pues puede tener muy buenas aplicaciones en ingenierías de todos tipos.