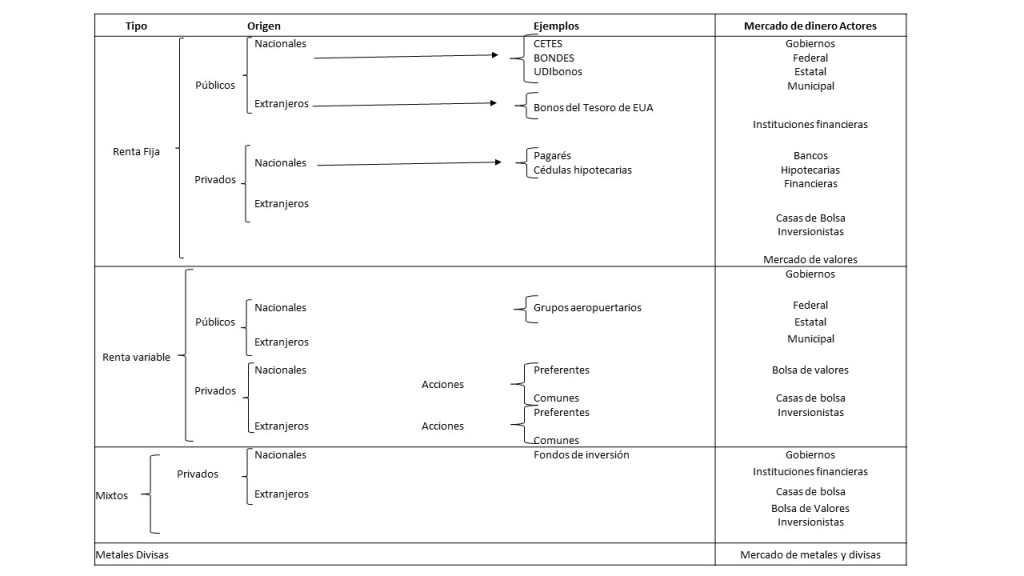
Introducción
En ésta sección se continuarán presentando algunas opciones de valores, que se utilizan con el mismo objetivo, obtener financiamiento, con la finalidad de conocer cuáles son la forma en que operan, las características que tienen, la forma en que se valúan, entre otros aspectos.
Descripción
Un bono redimible con pagos de dividendos, es un tipo de valor, el cual se caracteriza por pagar al inversionista, dividendos en cada periodo durante la duración de dicha operación, además de aportar una determinada cantidad cuando la duración de dicho valor culmine.
Los elementos que se manejan al operar con éste tipo de valor, son los siguientes:
- En su carátula se escribe el valor nominal del bono, también es conocido como valor de carátula y será representado por la letra P. Sin embargo, el valor nominal del bono, no representa necesariamente su valor monetario, sólo es una representación en unidades, que simboliza la participación de dicho bono en relación a la cantidad total emitida de dicho valor. Si, por ejemplo, se otorga un préstamo por la cantidad de \$10 mil pesos, con valor nominal de \$10 pesos cada bono, en tal situación se tienen una cantidad de mil bonos con ése valor nominal. Reiterando lo que se hace mención que no necesariamente representa su valor nominal, sino que solamente representa una milésima parte del préstamo. Éste tipo de comportamiento se asemeja al comportamiento que adoptan las acciones (son valores de renta variable) en una empresa cuando éstas representan el capital social que tiene, es decir, cada acción es una representación de una parte de dicho capital.
- El valor nominal de un bono no representa su valor teórico (éste comportamiento aplica también a las acciones de una empresa), «sólo es una forma de representar una proporción con respecto al préstamo total» Cánovas T. 2004.
- En cada bono queda acordado las cláusulas con las cuales serán pagados a los inversionistas mediante una tasa de dividendos, donde quedará asentada la periodicidad con la que se harán los pagos.
- El valor nominal de los bonos queda determinado por los dividendos futuros, y es a través de éstos que se calculará el valor presente o también conocido como valor de compra del bono. En el momento de hacer la compra, el inversionista, es cuando se calcula con una tasa de rendimiento estimada.
- El valor de redención, es la cantidad que se pagará cuando se termine la vigencia de éste valor. Si dicha cantidad es igual a la cantidad de compra, bajo esa condición se dice que el bono se vende a la par. Si el precio de compra es mayor, a la cantidad nominal, entonces se dice que el bono se vende arriba de par, y si es a la inversa, entonces se dice que se vende abajo de par.
- «El valor de redención, queda determinado como un porcentaje del valor nominal». De esta forma, el emisor puede pactar que el valor de redención sea de 105% del valor nominal. Cánovas T. 2004.
- Los dividendos que se pagan cada periodo quedan establecidos a través de una tasa conocida como tasa de dividendos, la cual se usa en el valor de redención. No se aplica en el valor de la carátula o valor nominal, porque sólo es una referencia que representa el porcentaje respecto al total emitido.
- La tasa de dividendos, se obtiene en tanto por ciento, que tiene periodicidad con la que se deberán pagar los dividendos durante la duración de la operación. Ésta tasa de dividendos, puede ser, por ejemplo, del 7% trimestral.
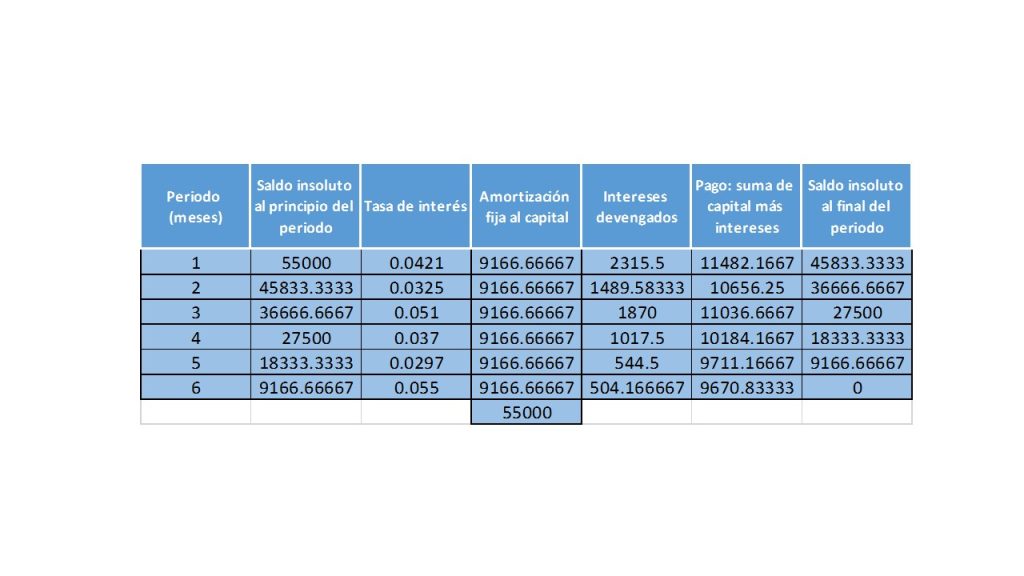
- De esta forma, si se le asigna la variable C para representar el valor de redención y la variable g a la tasa de dividendos (pagado por periodo mes, año, bimestre, etc.), se puede representar su comportamiento gráficamente por medio de la siguiente imagen:
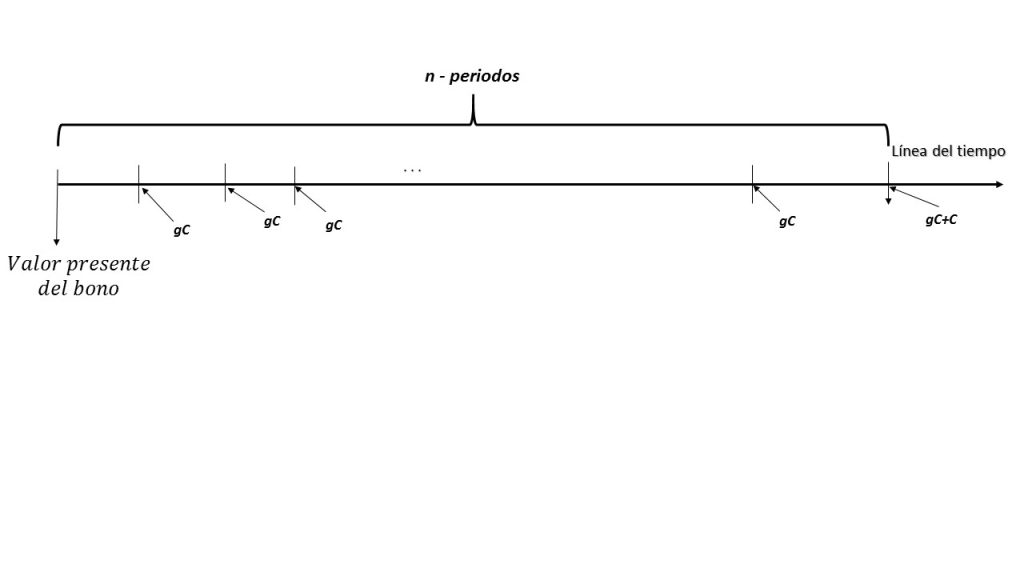
La variable con la se representará el valor presente del bono será V, mientras que la cantidad de por concepto de dividendo que se pagará se obtiene haciendo el producto de gC.
Suponiendo que la tasa de dividendos sea del 3% bimestral, y el valor de redención sea de \$110, con ésta el monto del dividendo se obtiene
$$(0.03)(100)= \$3 $$
dicha cantidad es la que se tendrá que pagar cada bimestre. Es importante señalar que el pago de dividendos, se hace de forma vencida y que la empresa, institución o inversionista que emita este tipo de bonos, es quien determina los pagos de dividendos así como el valor de redención, el cual se obtiene basándose en las utilidades futuras que se espera obtener, y en los flujos de efectivo que haya, que se tengan como resultado de la emisión y venta de dichos valores.
Por ejemplo, una empresa desea financiar un proyecto de una ampliación de sus instalaciones, para lograrlo busca un financiamiento, y solicita un préstamo por la cantidad de \$10 mil pesos, por lo cual emite 100 bonos, con un costo nominal de \$100 pesos cada uno. Consideran pagarlo en 25 meses y un pago de redención de \$110 al final del plazo, y dividendos anuales en efectivo de 18% (tasa de dividendo, g). del valor de redención, esto quiere decir que la cantidad que se pagará por este concepto es de $\$19.80$, por cada bono.
En el mismo ejemplo, si una empresa estuviera interesada en adquirir éstos valores (o éstos bonos), se pagaría por ellos la cantidad de:
$$(4)(110)+110=\$189.2$$
dinero que podría ser el pago para adquirir un bono. Bajo éste supuesto calculado al día de hoy, se muestra que bajo esas condiciones al comprador no le conviene hacer dicha compra, ya que para recuperar su dinero tendría que esperar 25 meses, sin ninguna otra recompensa o pago, por lo que le convendría mejor invertir en otra opción que le produjera mejores intereses.
Esto nos lleva a presentar la forma adecuada con la que se debe calcular el valor de compra de un bono, el cual consiste en traer a valor presente, a la fecha en que se realiza la compra, cada uno de los flujos de efectivo que representan el pago de los dividendos y por el pago final que es el valor de redención que realizará el emisor.
Para llevar a cabo el cálculo del valor presente, es necesario que para los dividendos como para el pago final, se fije una tasa de interés, misma que se pacta con la empresa (inversionista, institución), que realiza la compra, considerando aspectos de riesgo que represente la inversión, y que contempla además, las condiciones que tenga el mercado así como otras variables que estarán incluidas en la varia i, y que será denominada o conocida como tasa de rendimiento para diferenciarla de la tasa de interés. Una representa el interés que gana el inversionista y otra representa la cantidad que se espera ganar por hacer la compra.
«La tasa de rendimiento esperada se debe de tomar en cuenta para calcular el valor presente, tanto de los dividendos como del valor de redención del bono, para que con esto se pueda calcular el valor de compra. Con esto se garantiza que el inversionista obtenga su rendimiento deseado». (Cánovas T. 2003)
Vale la pena recordar que en el momento que se revisó el tema de anualidades, en el subtema que hacía referencia a la variación de tasas de interés en el valor presente de la anualidad. Si la tasa de interés aumenta, el valor presente disminuirá y viceversa, manteniendo una relación inversa. Este comportamiento ocurre debido a que los valores presentes se calculan con $v_i^t$, función que es inversa a la de acumulación $(1+i)^t$.
Bajo este contexto, si el inversionista planea un alto rendimiento en la inversión, pagará una menor cantidad por el bono. Sin embargo, si los deseos del inversionista es manejar tasas altas de rendimiento, entonces el vendedor recibirá menor cantidad de dinero por la colocación de sus bonos. Una situación semejante ocurre, si los compradores observan que los intereses bajan en el mercado, esto trae como consecuencia que se reduzca la tasa de rendimiento y que se pague una cantidad mayor por el bono que beneficiará más a favor emisor.
La tasa de rendimiento, para fines prácticos, debe ser utilizada efectiva por periodo manejando la misma periodicidad con la que se maneja al pago de los dividendos, por ejemplo, si los dividendos se pagan de forma semestral, la i, debe ser igual semestral.
Cabe hacer mención, que, si se llegase a dar el caso en el que el valor presente del bono, o precio de compra calculado con la tasa de rendimiento propuesta por el inversionista, resulta muy baja para el emisor, éste puede decidir que la venta no se realice; ya que como se había hecho mención, la idea principal de emitir bonos, es obtener una forma de financiamiento y el emisor tiene el derecho de aceptar pagar o no el costo que represente.
Retomando el ejemplo que se venía manejando, y la tasa de rendimiento que espera el inversionista tener sea del 16%, entonces el valor de compra del bono se podría calcular de tal como se muestra en la siguiente imagen:
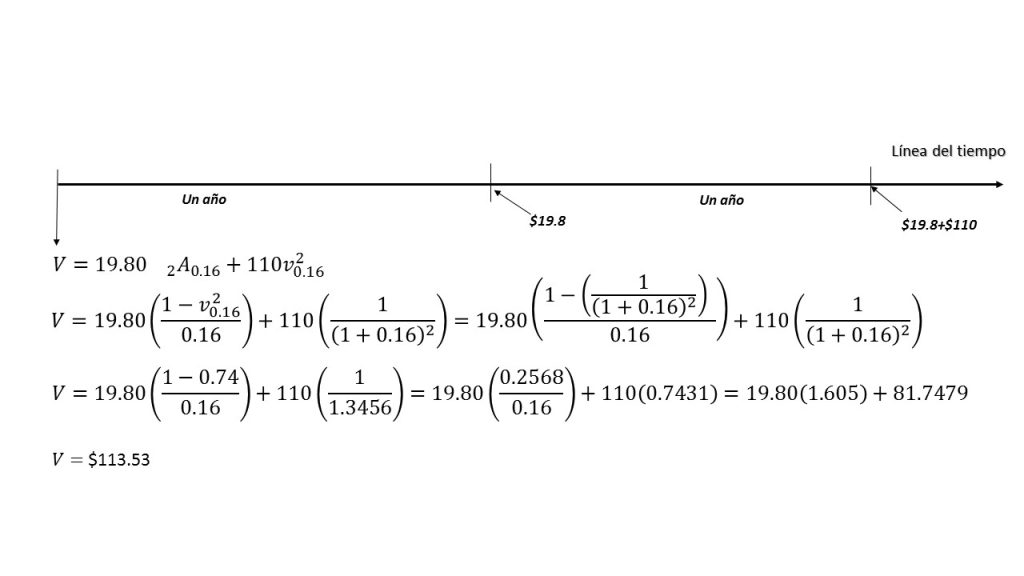
La cantidad aritmética que se obtiene de la suma de cada flujo de efectivo es de \$149.6 ya considerado en ella el valor de redención, en contraste con la cantidad obtenida que representa el valor de compra.
Bajo el procedimiento que se acaba de mostrar en la imagen anterior, es la forma en la que se puede determinar la ecuación general para poder valuar bonos redimibles con pago de dividendos. Cuando se haga la valuación en la fecha en la que se tiene considerado hacer la compra, en tal supuesto el valor que se obtendrá es el valor de compra del bono.
A continuación, se procederá a construir el modelo general para valuar bonos redimibles con pago de dividendos.
Partiendo del ejemplo de la imagen expuesta hace unos momentos, se tiene que el valor presente de los dividendos, así como el valor de redención con su respectiva tasa de interés, y haciendo uso de las variables g (tasa de dividendos), C (valor de redención sobre el que se calculan los dividendos), está representado por la siguiente ecuación:
$$V=gCv_i^1+gCv_i^2+gCv_i^3+…+gCv_i^{n-1}+gCv_i^{n}+Cv^n$$
De dicha expresión se factoriza gC en los n primeros términos, para obtener:
$$V=gC(v_i^1+v_i^2+v_i^3+…+v_i^{n-1}+v_i^n)+Cv_i^n$$
$$V=gC\prescript{}{n}{\mathbf{A}}_i+Cv_i^n$$
Ejercicios resueltos
Ejercicio. Una empresa de bienes raíces quiere financiar un proyecto de creación de una unidad habitacional, para lograrlo requiere la cantidad de 150 millones de pesos; y planea pagar dicha cantidad en 8 años. Para obtener dicha cantidad emite 5 millones de bonos los cuales serán pagados a los inversionistas con una cantidad del 53.5% del valor nominal, cantidad que se entregará al final junto con el pago de dividendos anuales equivalente al valor de redención del 6.4% y la tasa de rendimiento que se espera obtener es del 17%
Solución
Para resolver este ejercicio, es necesario mostrar que, la cantidad emitida de bonos fueron 5 millones, los cuales tienen el objetivo de poder financiar el proyecto de la construcción de la unidad habitacional, el cual considera un costo de 150 millones, de tal forma que el valor nominal de cada bono será:
$$\frac{150 millones}{5 millones}=30$$
Por otra parte, el emisor se comprometió a pagar el 53.5% a los inversionistas, entonces tendrá que pagar la cantidad de:
$$(30)(0.535)=16.05$$
Al final de la vigencia de dichos bonos, esto es después de 8 años.
Tomando en cuenta que los dividendos se pagan al final de cada año, y que de acuerdo con el emisor serán pagados con una tasa del 6.4% del valor de redención, entonces la cantidad que recibirán las personas que adquieran por cada bono al final de cada año, y durante la vigencia de ésto, es de:
$$(16.05)(0.064)=1.0272$$
La forma gráfica del comportamiento de ésta operación se muestra a continuación:
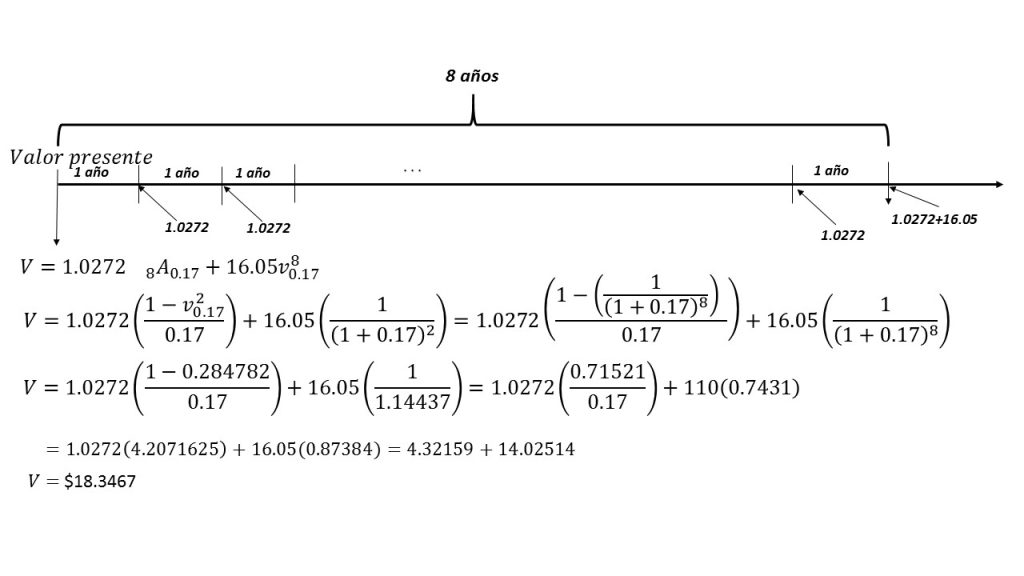
Más adelante…
Se continuarán abordando otros tipos de bonos, en donde se dará seguimiento a las aplicaciones prácticas de todas las herramientas que se han estado desarrollando.
- Matemáticas Financieras
- Entrada anterior
- Entrada siguiente