4.1 Razón cruzada para hilera y haces
Introducción
Ya se ha visto que en una hilera armónica se tienen cuatro puntos colineales $A,B,C,D$, donde el segmento $AB$ está dividido por $C$ y $D$ en razones cuya razón es:
$\hspace{15em} \frac{AC}{CB} / \frac{AD}{DB} = -1$
En este caso $A$ y $B$ están separados armónicamente por $C$ y $D$, pero que pasaría si estos cuatro puntos estuvieran en posiciones cualesquiera en la recta que se encuentran, es aquí donde entra la definición de razón cruzada.
Definición (Razón Cruzada)
Dados cuatro puntos colineales distintos $A,B,C,D$ en una recta, diremos que la razón cruzada es:
$\frac{AC}{CB} / \frac{AD}{DB} = \{ ABCD \} = k$ con $k \neq -1$
Lo denotaremos $\{ ABCD \} $.
También se le conoce como razón anarmónica y razón doble.
Observación
Si los cuatro puntos son armónicos, entonces $\{ ABCD \} = -1 $, de igual forma inversamente.
Definición (Razón Cruzada con líneas concurrentes)
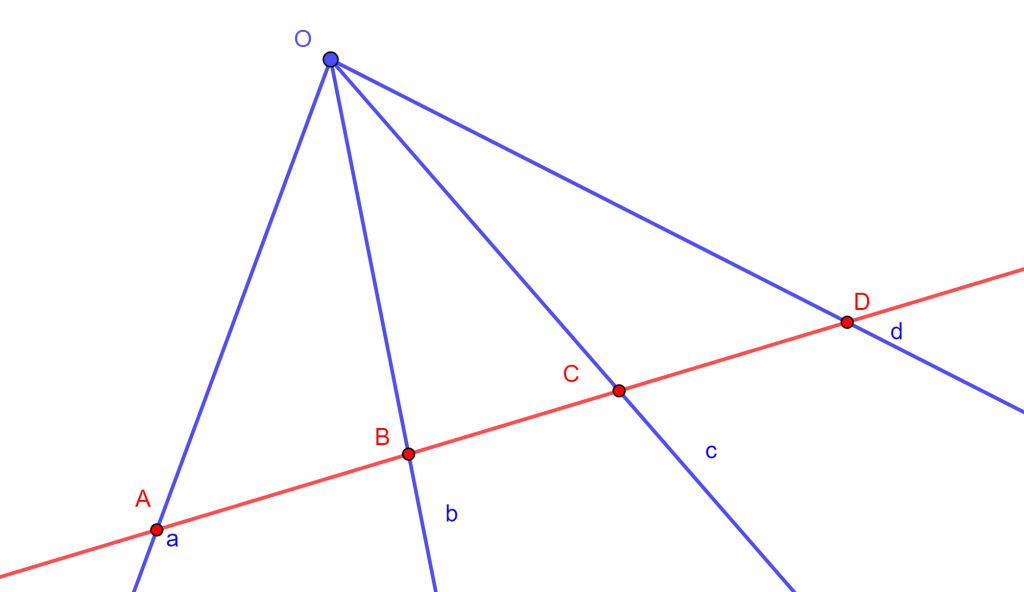
Sean cuatro rectas concurrentes $OA$, $OB$, $OC$ y $OD$ en un punto $O$, que no se forme un haz armónico, entonces la razón cruzada es:
$\frac{sen (AOC)}{sen (COB)} / \frac{sen (AOD)}{sen (DOB)} $,
se denotará como $O \{ ABCD \} $. De igual forma, la razón cruzada de cuatro líneas concurrentes $a,b,c,d$ se denotará $\{ a,b,c,d \} $.
Observación
Dados cuatro puntos colineales $A,B,C, D$ se tienen estos casos:
1) $\{ ABCC \} =1$ esto, ya que $\{ ABCC \} =\frac{AC}{CB} / \frac{AC}{CB} = \frac{AC * CB}{CB * AC} =1$.
2) $\{ ABCB \} =0$ esto ya que $\{ ABCB \} =\frac{AC}{CB} / \frac{AB}{BB} = \frac{AC * BB}{CB * AB} =0$.
3) $\{ ABCA \} =\infty $ esto ya que $\{ ABCA \} =\frac{AC}{CB} / \frac{AA}{AB} = \frac{AC * AB}{CB * AA} =\infty $.
Por lo cual se puede demostrar que si la razón cruzada de cuatro puntos tiene uno de los valores $1,0, \infty $ entonces dos de los puntos coinciden.
Teorema (Razón Cruzada)
Si se tienen cuatro puntos distintos $A,B,C,D$ en una recta y $O$ un punto (no está en la recta) entonces:
$\{ ABCD \} =O \{ ABCD \} $
Demostración
Para demostrar el teorema se usará lo siguiente, si dos puntos finitos $A$ y $B$ distintos en una recta, sea $P$ otro punto de la misma recta y $C$ un punto que no está en la recta, entonces
$\frac{AP}{PB}=\frac{CA*sen (ACP)}{CB*sen (PCB)}$
Entonces usando lo anterior:
$\frac{AC}{CB}=\frac{OA*sen (AOC)}{OB*sen (COB)}$ y $\frac{AD}{DB}=\frac{OA*sen( AOD)}{OB*sen (DOB)}$
$\{ ABCD \} = \frac{AC}{CB} / \frac{AD}{DB}=\frac{OA*sen(AOC)}{OB*sen(COB)} / \frac{OA*sen(AOD)}{OB*sen(DOB)}=\frac{sen(AOC)}{sen(COB)} / \frac{sen(AOD)}{sen( DOB)}=O \{ ABCD \}$ $_\blacksquare$
Corolarios
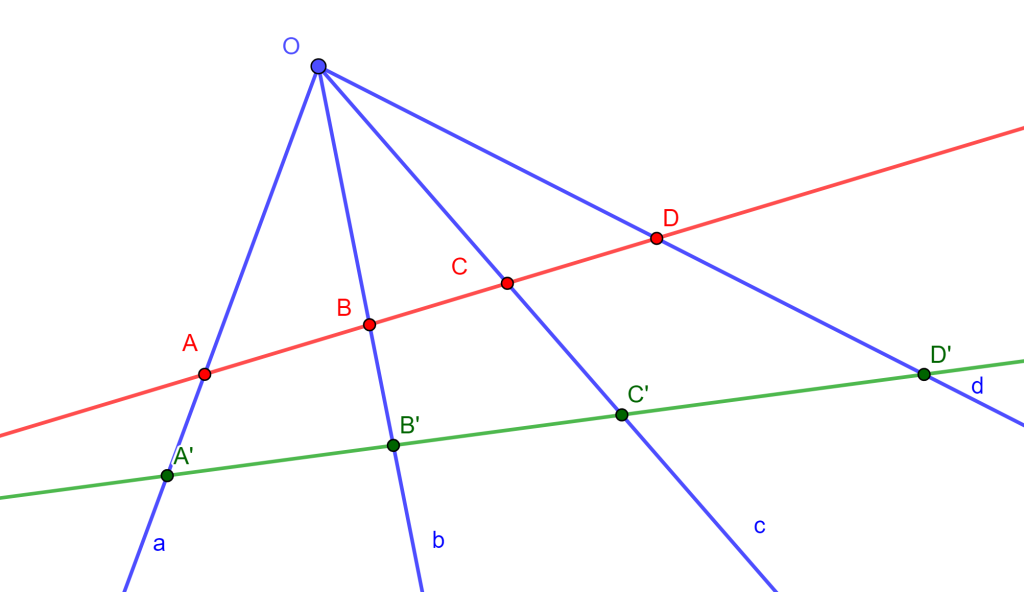
1) Sean dos rectas transversales a cuatro líneas de un haz, de las cuales ninguna pasa por el vértice, cortan a estas líneas en $A,B,C,D$ y $A’,B’,C’,D’$ respectivamente, entonces $\{ ABCD \} = \{ A’B’C’D’ \} $.
Demostración
$\{ ABCD \} = O\{ ABCD \} = O\{ A’B’C’D’ \} =\{ A’B’C’D’ \} $ $_\blacksquare$
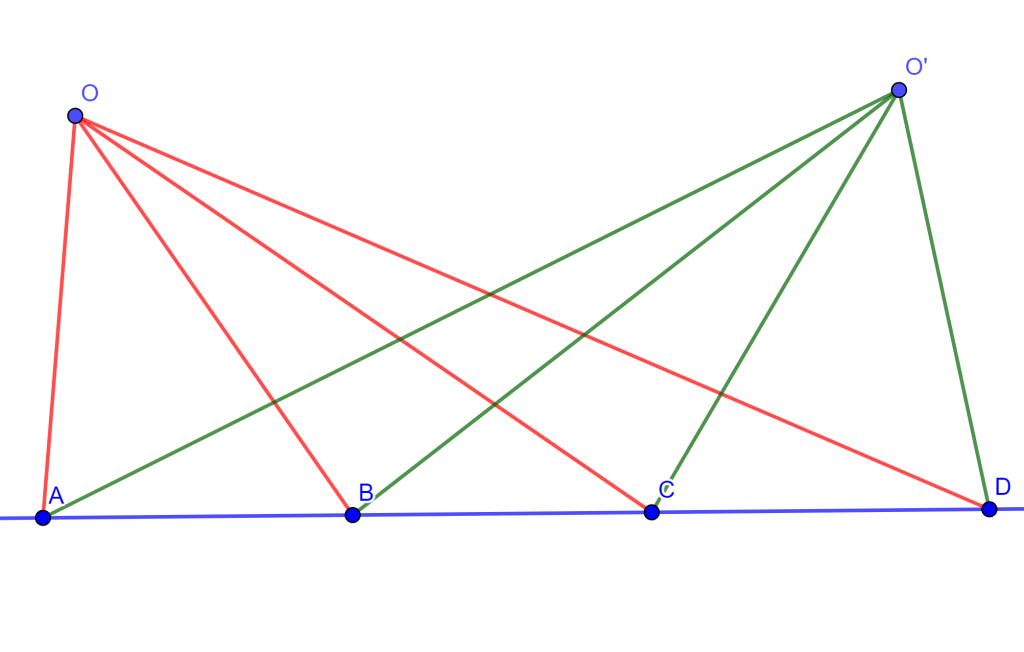
2) Sean dos haces con vertices en $O$ y $O’$ son subtendidos por la misma hilera de puntos $A,B,C,D$ entonces $O\{ ABCD \} = O’\{ ABCD \}$.
Demostración
$O\{ ABCD \} = \{ ABCD \}=O’\{ ABCD \}$ $_\blacksquare$
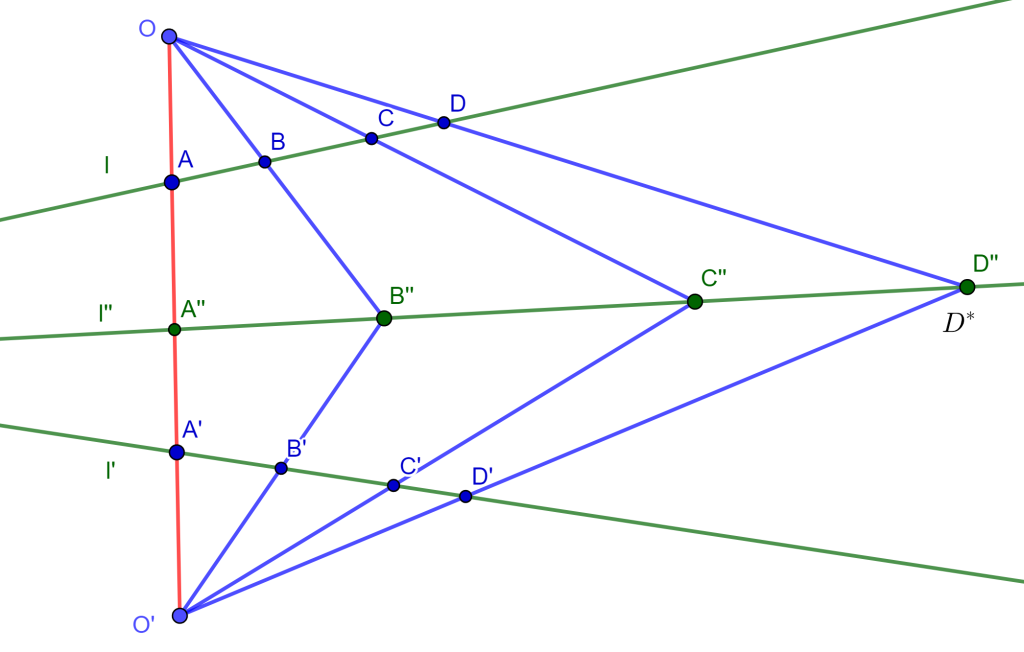
3) Sean $l$ y $l’$ dos rectas en posición cualquiera y sean $A,B,C,D \in l$ y $A’,B’,C’,D’ \in l’$. Si $\{ ABCD \} = \{ A’B’C’D’ \} $ y $O$ y $O’$ son colineales con $A$ y $A’$, entonces las intersecciones $OB$ y $O’B’$, $OC$ y $O’C’$, $OD$ y $O’D’$ son colineales.
Demostración
Sea $l’$$’$ la recta que contiene a $B’$$’$ y $C’$$’$, y sean $A’$$’=l’$$’ \cap OO’$, $D’$$’=OD \cap O’D’$ y sea $D^*=l’$$’ \cap O’D’$.
Tenemos que $\{ ABCD \} = \{ A’B’C’D’ \} $ entonces $\{ A’B’C’D’ \} = \{ A’$$’B’$$’C’$$’D^* \} $.
$\Rightarrow $ $\{ ABCD \} = \{ A’$$’B’$$’C’$$’D^* \} $
$\Rightarrow $ $O\{ ABCD \} = \{ A’$$’B’$$’C’$$’D^* \} $
$\Rightarrow $ $D’$$’=D^*$ $_\blacksquare$
Más adelante…
Se seguirá abordando unas propiedades de la razón cruzada y además se construirá un cuarto elemento dada una razón.
Entradas relacionadas
- Ir a Geometría Moderna II
- Entrada anterior del curso: Ejercicios Unidad 3
- Siguiente entrada del curso: Construcción del cuarto elemento dada la razón