Introducción
A lo largo de nuestros cursos de Cálculo hemos trabajado con el concepto de límite a detalle, ya que como sabemos, conceptos esenciales en la teoría de las funciones reales como el de continuidad y derivada, además de muchos otros, tienen sustento y se definen precisamente a través del límite. Intuitivamente sabemos que el límite de una función real, cuando existe, digamos $\lim\limits_{x\to x_0} f(x) = L$, nos dice que los valores de la función $f$ estarán tan cercanos al número real $L$ siempre que $x$ esté próximo a $x_0$, pero sin llegar a ser igual a dicho valor.
En esta entrada veremos que al igual que en el caso real, el concepto de límite para funciones complejas nos permitirá hablar de la continuidad y la diferenciabilidad de una función compleja. Aunque el concepto de límite para funciones complejas será idéntico a nuestra idea de proximidad en el caso real, veremos que el caso complejo es mucho más rico ya que aquí consideraremos más de dos posibles direcciones en que un número complejo se aproxime a otro.
Límite complejo
Recordemos que para $S\subset\mathbb{C}$, el conjunto $S’$ denota al conjunto de los puntos de acumulación de $S$.
Definición 14.1. (Límite de una función compleja.)
Sea $S \subset \mathbb{C}$ y sea $z_0 \in S’$. Dada $f\in\mathcal{F}(S)$, diremos que el número complejo $L\in\mathbb{C}$ es el límite de $f(z)$ cuando z tiende a $z_0$, lo cual denotamos como $\lim\limits_{z\to z_0} f(z) = L$, si para todo $\varepsilon>0$ existe un $\delta>0$ tal que si $z\in S$ y $0<|\,z – z_0\,|<\delta$ entonces $|\,f(z) – L\,|<\varepsilon$.
Observación 14.1.
En caso de existir el límite, este es único. Supongamos que $\lim\limits_{z \to z_0} f(z) = L_1$ y $\lim\limits_{z \to z_0} f(z) = L_2$. Por la definición 14.1 tenemos que dado $\varepsilon>0$ existen $\delta_1>0$ y $\delta_2>0$ tales que si $z\in S$ y $0<|\,z – z_0\,|<\delta_1$, $0<|\,z – z_0\,|<\delta_2$, entonces $|\,f(z) – L_1\,|<\frac{\varepsilon}{2}$ y $|\,f(z) – L_2\,|<\frac{\varepsilon}{2}$. Como $z_0 \in S’$, entonces para $\delta = \text{mín}\{\delta_1, \delta_2\} > 0$ existe $z^* \in S$ tal que $0<|\,z^* – z_0\,| < \delta$, por lo que: \begin{equation*} |\,L_1 – L_2\,| \leq |\,f(z^*) – L_1\,| + |\,f(z^*) – L_2\,| < \varepsilon. \end{equation*} Como se cumple para todo $\varepsilon>0$, entonces $L_1 = L_2$.
Observación 14.2.
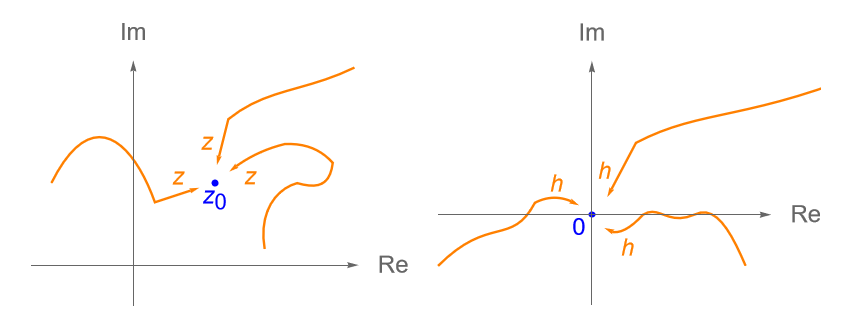
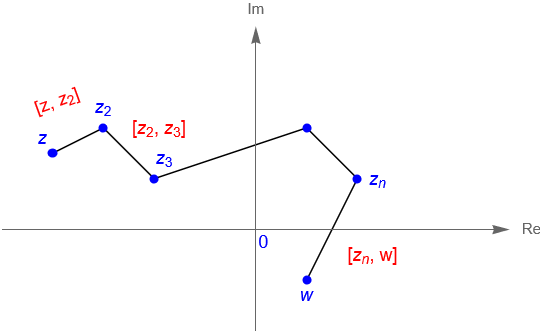
Primeramente, notemos que la existencia del límite $L$ no depende de que la función $f$ esté definida en el punto $z_0$. Por otra parte, de acuerdo con la observación 14.1 tenemos que para garantizar la existencia de $\lim\limits_{z \to z_0} f(z)$, debe suceder que la función $f$ evaluada en $z$ se aproxime siempre al mismo número complejo $L$, esto sin importar la forma en que $z$ se aproxime a $z_0$, figura 68. Es decir, si $f$ se aproxima a dos números complejos distintos, digamos $L_1$ y $L_2$, cuando $z$ se aproxima a $z_0$ siguiendo dos trayectorias distintas, entonces $\lim\limits_{z \to z_0} f(z)$ no existe.

Ejemplo 14.1.
a) Consideremos la siguiente función: \begin{equation*} f(z)= \dfrac{z^2 + 4}{z-2i}. \end{equation*} Es claro que el dominio natural de $f$ es $S = \mathbb{C} \setminus\{2i\}$. Sin embargo, veamos que $\lim\limits_{z \to 2i} f(z) = 4i$.
Solución. Sea $z \in S$. Notemos que: \begin{equation*} \dfrac{z^2 + 4}{z-2i} \,-\, 4i = \dfrac{(z+2i)(z-2i)}{z-2i} \,- \, 4i = z – 2i, \end{equation*} por lo que:
\begin{equation*}|\,f(z) – 4i\,| = |\,z – 2i\,|. \end{equation*} Entonces para $\varepsilon>0$ definimos $\delta = \varepsilon$, entonces $|\,f(z) – 4i\,|<\varepsilon$ si $0<|\,z – 2i\,|<\delta$, es decir $\lim\limits_{z \to 2i} f(z) = 4i$.
b) Consideremos a la función $f(z) = \overline{z}^2 – 2$. Es claro que la función $f$ está definida en todo $\mathbb{C}$. Veamos que $\lim\limits_{z\to 1-i} f(z) = -2 + 2i$.
Solución. Sean $z\in\mathbb{C}$ y $\varepsilon>0$. Notemos que: \begin{align*}|\,\overline{z}^2 – 2 -(-2+2i)\,| & = |\,\overline{z}^2 – 2i\,| = |\,\overline{\overline{z}^2 – 2i}\,| = |\,z^2 + 2i\,|\\ & = |\,z-(1-i)\,| \, |\,z+(1-i)\,|\\
&\leq |\,z-(1-i)\,| \, \bigg( |\,z-(1-i)\,| + 2|\,1-i\,| \bigg). \end{align*} Haciendo $0<|\,z-(1-i)\,|<1$ tenemos que: \begin{align*} |\,\overline{z}^2 – 2 -(-2+2i)\,| &\leq |\,z-(1-i)\,| \, \bigg( 1 + 2\sqrt{2} \bigg) \end{align*} Por lo que tomando $\delta= \text{mín}\left\{1, \dfrac{\varepsilon}{1+2\sqrt{2}}\right\}>0$, se sigue que si $0<|\,z-(1-i)\,|<\delta$ entonces: \begin{equation*} |\,f(z) – (-2+i)\,| = |\,\overline{z}^2 – 2 -(-2+2i)\,| < \varepsilon. \end{equation*} Por lo tanto $\lim\limits_{z\to 1-i} f(z) = -2 + 2i$.
c) Sea $c\in\mathbb{C}$ una constante. Consideremos a las funciones $f(z) = c$, $g(z)=z$ y $h(z)=\overline{z}$. Es claro que dichas funciones complejas están definidas en todo $\mathbb{C}$. Entonces para todo $z_0\in\mathbb{C}$ se cumple que para todo $\varepsilon>0$ existe $\delta = \varepsilon>0$ tal que: \begin{align*} \lim_{z \to z_0} f(z) = c,\\ \lim_{z \to z_0} g(z) = z_0,\\ \lim_{z \to z_0} h(z) = \overline{z_0}. \end{align*}
Ejemplo 14.2.
Consideremos a la función: \begin{equation*} f(z) = \dfrac{z}{\overline{z}}, \end{equation*} cuyo dominio es $S =\mathbb{C}\setminus\{0\}$. Veamos que $\lim\limits_{z\to 0} f(z)$ no existe.
Solución. De acuerdo con la observación 14.2, basta encontrar dos trayectorias por las que $z$ se aproxime a $0$ que nos den valores distintos para dicho límite.
Notemos que si nos acercamos a $0$ a través del eje real, es decir tomando $z=x+i0$, con $x\rightarrow 0$, entonces: \begin{equation*} \lim_{z \to 0} f(z) = \lim_{z \to 0} \dfrac{z}{\overline{z}} = \lim_{x \to 0} \dfrac{x+i0}{x-i0} = \lim_{x \to 0} \dfrac{x}{x} = 1. \end{equation*}
Mientras que si nos acercamos a $0$ a través del eje imaginario, es decir tomando $z=0+iy$, con $y\rightarrow 0$, entonces: \begin{equation*} \lim_{z \to 0} f(z) = \lim_{z \to 0} \dfrac{z}{\overline{z}} = \lim_{y \to 0} \dfrac{0+iy}{0-iy} = \lim_{y \to 0} \dfrac{iy}{-iy} = -1. \end{equation*}
Por lo que $\lim\limits_{z\to 0} f(z)$ no existe.
Observación 14.3.
De acuerdo con la proposición 8.6 de la entrada 8, tenemos que para $z_0\in\mathbb{C}$ y $S\subset\mathbb{C}$ se cumple que $z_0$ es un punto de acumulación de $S$ si y solo si existe una sucesión $\{z_n\}_{n \geq 1}$ en $S$ tal que $z_n \neq z_0$ para todo $n\in \mathbb{N}^+$ y $\lim\limits_{n\to \infty} z_n = z_0$.
Este resultado es útil para caracterizar la existencia del límite de una función compleja a través de sucesiones complejas, para ello planteamos la siguiente:
Proposición 14.1.
Sean $S \subset \mathbb{C}$, $z_0\in S’$, $L\in\mathbb{C}$ y $f\in\mathcal{F}(S)$ una función. Entonces se cumple que $\lim\limits_{z \to z_0} f(z) = L$ si y solo si $\lim\limits_{n \to \infty} f(z_n) = L$, para toda sucesión $\{z_n\}_{n \geq 1} \subset S$ tal que $z_n \neq z_0$ para todo $n\in \mathbb{N}^+$ y $\lim\limits_{n\to \infty} z_n = z_0$.
Demostración. Dadas las hipótesis tenemos:
$\Rightarrow)$
Supongamos que $\lim\limits_{z \to z_0} f(z) = L$. Veamos que $\lim\limits_{n \to \infty} f(z_n) = L$, para toda sucesión $\{z_n\}_{n \geq 1} \subset S$ tal que $z_n \neq z_0$ para todo $n\in \mathbb{N}^+$ y $\lim\limits_{n\to \infty} z_n = z_0$.
Dado $\varepsilon>0$ existe $\delta>0$ tal que si $z\in S$ y $0<|z-z_0|<\delta$, entonces $0<|f(z)-L|<\varepsilon$.
Sea $\{z_n\}_{n\geq 1}\subset S$ una sucesión tal que $z_n \neq z_0$ para todo $n\in\mathbb{N}^+$ y $\lim\limits_{n \to \infty} z_n = z_0$. Para $\delta>0$ se cumple para toda $n\geq N$ que $0<|\,z_n – z_0\,|<\delta$. Por lo tanto: \begin{equation*} |\,f(z_n) – L\,| < \varepsilon, \quad \forall n\geq N, \end{equation*} es decir que $\lim\limits_{n \to \infty} f(z_n) = L$.
$(\Leftarrow$
Supongamos que para toda sucesión $\{z_n\}_{n \geq 1} \subset S$ tal que $z_n \neq z_0$ para todo $n\in \mathbb{N}^+$ y $\lim\limits_{n\to \infty} z_n = z_0$, se cumple que $\lim\limits_{n \to \infty} f(z_n) = L$. Veamos que $\lim\limits_{z \to z_0} f(z) = L$.
Por reducción al absurdo supongamos que $\lim\limits_{z \to z_0} f(z) \neq L$. Entonces existe $\varepsilon>0$ tal que para todo $\delta>0$ existe $z_\delta \in S$ tal que $0<|\,z_\delta – z_0\,| < \delta$ y $0<|\,f(z_\delta) – L\,| \geq \varepsilon$.
Dado que para toda $n\in \mathbb{N}^+$ se cumple que $\frac{1}{n}$ es positivo, entonces existe $z_n \in S$ tal que: \begin{equation*} 0<|\,z_n – z_0\,|<\frac{1}{n} \quad \text{y} \quad |\,f(z_n) – L\,| \geq \varepsilon, \end{equation*} es decir que la sucesión $\{z_n\}_{n\geq 1}$, con $z_n \neq z_0$ para todo $n\in\mathbb{N}^+$, converge a $z_0$, pero la sucesión $\{f(z_n)\}_{n\geq 1}$ no converge a $L$, lo cual contradice nuestra hipótesis, por lo que $\lim\limits_{z \to z_0} f(z) = L$.
$\blacksquare$
Observación 14.4.
De acuerdo con la proposición 12.1 de la entrada 12, sabemos que toda función compleja $f$ puede escribirse de la forma: \begin{equation*} f(z) = u(x,y) + i v(x,y), \end{equation*} con $u(x,y)$ y $v(x,y)$ funciones reales que corresponden con su parte real e imaginaria, respectivamente. Veamos que podemos garantizar la existencia del límite de una función compleja a través de estas funciones, para ello recordemos primeramente la definición de límite para una función real de dos variables, vista en nuestros cursos de Cálculo.
Definición 14.2. (Límite de una función real de dos variables.)
Sean $U\subset\mathbb{R}^2$ un conjunto abierto y $u: U\to \mathbb{R}$ una función real de dos variables, digamos $x$ e $y$. Para $(x_0, y_0) \in U’$ y $a\in \mathbb{R}$ diremos que: \begin{equation*} \lim_{(x,y) \to (x_0, y_0)} u(x,y) = a, \end{equation*} si para todo $\varepsilon>0$ existe $\delta>0$ tal que si $(x,y)\in U$ y $0<\sqrt{(x-x_0)^2 + (y-y_0)^2} < \delta$, entonces: \begin{equation*} |u(x,y) – a| < \varepsilon. \end{equation*}
Proposición 14.2.
Sean $S\subset\mathbb{C}$, $z_0=x_0+iy_0\in S’$ y $L=a+ib\in\mathbb{C}$. Entonces para toda función compleja $f(z) = u(z)+iv(z)$ definida en $S$ se cumple que: \begin{equation*} \lim_{z \to z_0} f(z) = L \quad \text{si y solo si} \quad \lim_{z \to z_0} u(z) = a \,\,\, \text{y} \,\, \lim_{z \to z_0} v(z) = b. \end{equation*}
Demostración. Dadas las hipótesis, de acuerdo con la observación 3.1 tenemos que para todo $z=x+iy\in S$ se cumple que: \begin{equation*} |\,u(z) – a\,| \leq |\,f(z) – L\,| \leq |\,u(z) – a\,| + |\,v(z) – b\,|, \end{equation*} \begin{equation*} |\,v(z) – b\,| \leq |\,f(z) – L\,| \leq |\,u(z) – a\,| + |\,v(z) – b\,|. \end{equation*} Considerando las definiciones 14.1, 14.2 y las desigualdades anteriores se sigue el resultado.
$\blacksquare$
De acuerdo con la proposición 14.2, tenemos que la existencia de un límite en $\mathbb{C}$ está garantizada por la existencia de los límites de dos funciones reales, por lo que podemos utilizar los resultados que conocemos para límites de funciones reales de dos variables para verificar si dicho límite existe en $\mathbb{C}$.
Ejemplo 14.3.
Consideremos a la función $f(z) = z^2$, la cual está definida en todo $\mathbb{C}$. Veamos que para todo $z_0\in\mathbb{C}$ se cumple: \begin{equation*} \lim_{z \to z_0} f(z) = z_0^2. \end{equation*}
Solución. Procediendo por la definición 14.1 es fácil probar la existencia de dicho límite. Sin embargo, podemos hacer uso de la proposición 14.2 para probar el resultado.
Sean $z=x+iy, z_0 = x_0+iy_0 \in \mathbb{C}$ con $z_0$ fijo. Entonces tenemos que: \begin{equation*} f(x+iy) = u(x,y) + iv(x,y), \end{equation*} donde $\operatorname{Re}(f(z)) = u(x,y) = x^2 -y^2$ e $\operatorname{Im}(f(z))=v(x,y) = 2xy$. Tenemos que: \begin{align*} \lim_{z \to z_0} \operatorname{Re}(f(z)) = \lim_{\substack{x \to x_0 \\ y \to y_0}} u(x,y) = x_0^2 – y_0^2,\\ \lim_{z \to z_0} \operatorname{Im}(f(z)) = \lim_{\substack{x \to x_0 \\ y \to y_0}} v(x,y) = 2x_0 y_0. \end{align*} Por lo tanto $\lim\limits_{z \to z_0} f(z) = x_0^2 – y_0^2 + i2x_0y_0 = z_0^2$.
Observación 14.5.
Notemos que para la función $f(z)=z^n$, con $n\in\mathbb{N}^+$ y $z\in\mathbb{C}$, se puede probar por inducción que para todo $z_0\in\mathbb{C}$: \begin{equation*} \lim_{z \to z_0} f(z) = \lim_{z \to z_0} z^n = z_0^n. \end{equation*}
Proposición 14.3. (Álgebra de límites.)
Sean $f,g\in\mathcal{F}(S)$, sea $z_0 \in S’$ y sean $c, L_1, L_2 \in \mathbb{C}$. Supongamos que $\lim\limits_{z \to z_0} f(z) = L_1$, $\lim\limits_{z \to z_0} g(z) = L_2$. Entonces:
- $\lim\limits_{z \to z_0} \left[f(z) \pm c g(z)\right] = L_1 \pm c \, L_2$.
- $\lim\limits_{z \to z_0} \left[f(z)g(z)\right] = L_1L_2$.
- Si $L_2 \neq 0$, entonces $\lim\limits_{z \to z_0} \left[\dfrac{f(z)}{g(z)}\right] = \dfrac{L_1}{ L_2}$.
Demostración. Dadas las hipótesis, tenemos que:
- Si $c = 0$ entonces se sigue el resultado. Supongamos que $c\neq 0$ y sea $\varepsilon>0$, entonces existen $\delta_1>0$, $\delta_2>0$ tales que si $z\in S$ y $0<|\,z-z_0\,|<\delta_1$, $0<|\,z-z_0\,|<\delta_2$, entonces: \begin{align*} |\,f(z) – L_1\,| < \frac{\varepsilon}{2},\\ |\,g(z) – L_2\,| < \frac{\varepsilon}{2|c|}. \end{align*} Por lo que tomando $\delta = \text{mín}\{\delta_1, \delta_2\}>0$, tenemos que si $z\in S$ y $0<|\,z-z_0\,|<\delta$, entonces: \begin{equation*} |\,f(z) \pm cg(z) – (L_1 \pm c \, L_2) \,| \leq |\,f(z) – L_1\,| + |\,c\,| \, |\,g(z) – L_2\,| < \varepsilon. \end{equation*}
- Se deja como ejercicio al lector.
- Se deja como ejercicio al lector.
$\blacksquare$
Observación 14.6.
De acuerdo con la proposición 14.3 y el inciso (c) del ejemplo 14.1, podemos calcular de forma inmediata el límite de un polinomio en cualquier punto, o el límite de una función racional en un punto donde dicha función esté definida, simplemente evaluando el polinomio o la función racional en el punto dado.
Ejemplo 14.4.
Hallar cada uno de los siguientes límites:
a) $\lim\limits_{z \to 3i} \dfrac{z^2 + 9}{z – 3i}$.
b) $\lim\limits_{z \to 2+3i} (z – 5i)^2$.
c) $\lim\limits_{z \to i} 3z^2 + 2z -1$.
Solución. Considerando la observación 14.6 y las propiedades de los límites tenemos:
a) \begin{align*} \lim_{z \to 3i} \dfrac{z^2 + 9}{z – 3i} & = \lim_{z \to 3i} \dfrac{(z + 3i)(z – 3i)}{z – 3i}\\ & = \lim_{z \to 3i} z + 3i\\ & = \lim_{z \to 3i} z + \lim_{z \to 3i} 3i\\ & = 3i + 3i\\ & = 6i. \end{align*}
b) \begin{align*} \lim_{z \to 2+3i} (z – 5i)^2 & = \lim_{z \to 2+3i} (z – 5i)(z – 5i)\\ & = \left(\lim_{z \to 2+3i} z – 5i\right)^2\\ & = \left(\lim_{z \to 2+3i} z – \lim_{z \to 2 + 3i} 5i \right)^2\\ & = \left(2 + 3i – 5i \right)^2\\ & = \left( 2 – 2i\right)^2\\ & = -8i. \end{align*}
c) \begin{align*} \lim_{z \to i} 3z^2 + 2z – 1 & = 3 \lim_{z \to i} z^2 + 2\lim_{z \to i} z – \lim_{z \to i} 1\\ & = 3\left( \lim_{z \to i} z\right)^2 + 2i – 1\\ & = 3i^2 + 2i – 1 \\ & = -4 + 2i. \end{align*}
De acuerdo con la proposición 14.3, tenemos que las propiedades de los límites para funciones reales se extienden para el caso complejo. Veamos que otras propiedades de los límites para funciones reales pueden ser modificadas para el caso de funciones complejas.
Proposición 14.4. (Teorema de comparación.)
Sean $S\subset\mathbb{C}$, $f,g\in\mathcal{F}(S)$ dos funciones y $z_0\in S’$.
- Si $\lim\limits_{z\to z_0} f(z)=0$ y para algún $r>0$ se cumple que $|\,g(z)\,| \leq |\,f(z)\,|$ para toda $z\in B(z_0,r)\setminus\{z_0\}$, entonces $\lim\limits_{z\to z_0} g(z)=0$.
- Si $\lim\limits_{z\to z_0} f(z)=0$ y para algún $r>0$ se cumple que existe $M>0$ tal que $|\,g(z)\,| \leq M$ para toda $z\in B(z_0,r)\setminus\{z_0\}$, entonces $\lim\limits_{z\to z_0} f(z) g(z) =0$.
Demostración. Dadas la hipótesis, tenemos que:
- Para $\varepsilon>0$ existe $\delta>0$ tal que si $z\in S$ y $0<|\,z-z_0\,|<\delta$, entonces $|\,f(z)\,|<\varepsilon$. Sea $z\in B(z_0,\delta)\setminus\{z_0\}$, entonces $|\,g(z)\,| \leq |\,f(z)\,|$, por lo que $|\,g(z) – 0\,| < \varepsilon$ siempre que $0<|\,z-z_0\,|<\delta$, es decir $\lim\limits_{z\to z_0} g(z)=0$.
- Para $\varepsilon>0$ existe $\delta>0$ tal que si $z\in S$ y $0<|\,z-z_0\,|<\delta$, entonces $|\,f(z)\,|<\varepsilon$. Dado que para $z\in B(z_0,\delta)\setminus\{z_0\}$ se cumple que existe $M>0$ tal que $|\,g(z)\,| \leq M$, entonces para $0<|\,z-z_0\,|<\delta$ tenemos que: \begin{equation*} 0 \leq |\,f(z) g(z)\,| \leq M |\,f(z)\,|. \end{equation*} De acuerdo con el ejercicio 3 de esta entrada y la proposición 14.3(2) tenemos que $\lim\limits_{z\to z_0} M |f(z)| =0$, entonces considerando el inciso anterior se cumple que $\lim\limits_{z\to z_0} f(z) g(z) =0$.
$\blacksquare$
Consideremos ahora a la función $f(z) = 1/z$, dada en el ejemplo 12.1(d). Al pensarla como una función compleja definida en $\mathbb{C}$, es claro que el dominio $S$ de dicha función es $S = \mathbb{C}\setminus\{0\}$. Sin embargo, considerando al plano complejo extendido tomemos $f:S\subset\mathbb{C}_\infty \to \mathbb{C}_\infty$, por lo que podemos definir a la imagen de $z=0$ bajo dicha función como el punto al infinito, es decir $w = f(z) = \infty$. Es claro que al trabajar con $\mathbb{C}_\infty$ la función f es biyectiva, por lo que podemos pensar en la inversa de $f$, es decir en $z = f^{-1}(w) = 1/w$. Entonces ¿qué pasa con $\lim\limits_{w\to 0} f(f^{-1}(w))$? ¿y con $\lim\limits_{z \to \infty} f(z)$? ¿Qué relación hay entre dichos límites?
Por otra parte, como vimos en la entrada 11, cuando pensamos en que un número complejo tiende a infinito, lo cual denotamos como $z \to \infty$, estamos considerando que su módulo crece de manera arbitraria, es decir $|\,z\,| \to \infty$. Del mismo modo al hablar de una función $f$ que tiende a infinito, lo cual denotamos como $f(z) \to \infty$, estamos considerando que el módulo de dicha función crece de forma arbitraria, es decir $|\,f(z)\,| \to \infty$.
Para formalizar todo lo anterior consideremos las siguientes definiciones.
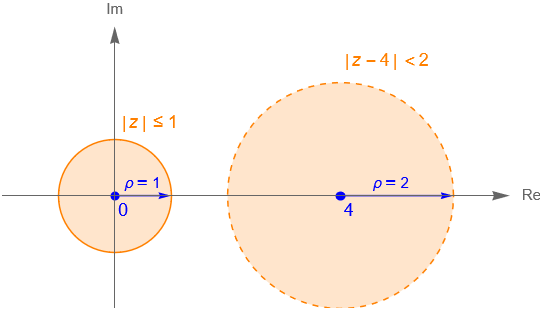
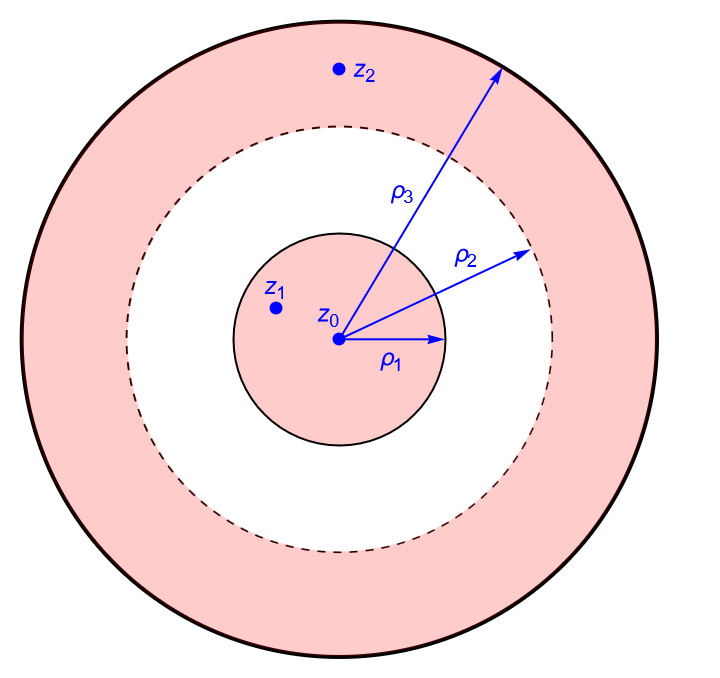
Definición 14.3. ($\rho$-vecindad de $\infty$.)
Sea $\rho>0$ suficientemente pequeño. En el plano complejo extendido $\mathbb{C}_\infty$, una $\rho$-vecindad de $\infty$ o simplemente una vecindad de $\infty$, es el conjunto: \begin{equation*} B(\infty, \rho) = \left\{z\in\mathbb{C} \,: \, \frac{1}{\rho} < |\,z\,| \right\}. \end{equation*} Un conjunto $U\subset\mathbb{C}_\infty$ abierto que contenga a una $\rho$-vecindad de $\infty$, para algún $\rho>0$, es también una $\rho$-vecindad de $\infty$.
Definición 14.4. (Límites al infinito e infinitos.)
Sea $f:S\subset\mathbb{C} \to \mathbb{C}$ una función.
- Diremos que $\lim\limits_{z\to \infty} f(z) = w_0$ si para todo $\varepsilon>0$, existe $\delta>0$ tal que si $z\in S$ y $|\,z\,|>\frac{1}{\delta}$, entonces: \begin{equation*} |\,f(z) – w_0\,| < \varepsilon. \end{equation*}
- Diremos que $\lim\limits_{z\to z_0} f(z) = \infty$ si para todo $\varepsilon>0$ existe un $\delta>0$ tal que si $z\in S$ y $0<|\,z-z_0\,|<\delta$, entonces: \begin{equation*} |\,f(z)\,| > \frac{1}{\varepsilon}. \end{equation*}
- Diremos que $\lim\limits_{z\to \infty} f(z) = \infty$ si para todo $\varepsilon>0$, existe $\delta>0$ tal que si $z\in S$ y $|\,z\,|>\frac{1}{\delta}$, entonces: \begin{equation*} |\,f(z)\,| > \frac{1}{\varepsilon}. \end{equation*}
Ejemplo 14.5.
a) Sea $f(z) = \dfrac{1}{z^2}$, con $z\neq 0$, entonces: \begin{equation*} \lim_{z\to \infty} f(z) = 0. \end{equation*} Solución. Sea $\varepsilon>0$. Notemos que para $\delta=\sqrt{\varepsilon}>0$, si $z\neq 0$ y $|\,z\,| > \dfrac{1}{\delta}$, entonces: \begin{equation*} \left|\,f(z) – 0\,\right| = \left|\,\frac{1}{z^2} – 0\,\right| = \frac{1}{|\,z^2\,|} = \frac{1}{|\,z\,|^2} < \varepsilon. \end{equation*} Por lo que $\lim\limits_{z\to \infty} f(z) = 0$.
b) Sea $f(z) = \dfrac{1}{z-3}$, con $z\neq 3$, entonces: \begin{equation*} \lim_{z\to 3} f(z) = \infty. \end{equation*} Solución. Sea $\varepsilon>0$. Notemos que para $\delta=\varepsilon>0$, si $z\neq 3$ y $0<|\,z-3\,|<\delta$, entonces: \begin{equation*} \left|\,f(z)\,\right| = \left|\,\frac{1}{z-3}\,\right| = \frac{1}{|\,z-3\,|} > \frac{1}{\varepsilon}. \end{equation*} Por lo que $\lim\limits_{z\to 3} f(z) = \infty$.
De lo anterior tenemos que los valores $z_0$ y $L$ en la definición 14.1 pueden ser sustituidos de forma indistinta por el punto al infinito, es decir en: \begin{equation*} \lim_{z \to z_0} f(z) = L, \end{equation*} podemos remplazar a $z_0$ y/o $L$ por $\infty$, para ello solo habría que remplazar apropiadamente sus vecindades por vecindades de $\infty$. Para tener más claro esto y poder trabajar de manera más sencilla con estos límites tenemos el siguiente resultado.
Proposición 14.5.
Sea $f:S \subset \mathbb{C} \to \mathbb{C}$ una función y sean $z_0$ en el plano $z$, que corresponde al del dominio de $f$, y $w_0$ en el plano $w$, que corresponde al plano de la imagen de $f$, observación 12.1, entonces:
- \begin{equation*} \lim_{z \to z_0} f(z) = \infty \quad \text{si y solo si} \quad \lim_{z \to z_0} \frac{1}{f(z)} = 0. \end{equation*}
- \begin{equation*} \lim_{z \to \infty} f(z) = w_0 \quad \text{si y solo si} \quad \lim_{z \to 0} f\left(\frac{1}{z}\right) = w_0. \end{equation*}
- \begin{equation*} \lim_{z \to \infty} f(z) = \infty \quad \text{si y solo si} \quad \lim_{z \to 0} \frac{1}{f(1/z)} = 0. \end{equation*}
Demostración. Dadas las hipótesis, tenemos que:
- Sea $z\in S$. Si $\lim\limits_{z \to z_0} f(z) = \infty$ existe, entonces de la definición 14.4(2) tenemos que para todo $\varepsilon>0$, existe $\delta>0$ tal que: \begin{equation*} |\,f(z)\,| > \frac{1}{\varepsilon} \quad \text{si} \quad 0<|\,z-z_0\,|<\delta. \end{equation*} Notemos que para el punto $w=f(z)$ se tiene que $|\,w\,| > 1/\varepsilon$, es decir $w$ pertenece a un $\varepsilon$-vecindario de $\infty$, siempre que $0<|\,z-z_0\,|<\delta$. De lo anterior tenemos que: \begin{equation*} \left|\,\frac{1}{f(z)} – 0 \,\right| = \left|\,\frac{1}{f(z)}\,\right| = \frac{1}{|f(z)|} < \varepsilon \quad \text{si} \quad 0<|\,z-z_0\,|<\delta. \end{equation*} Por lo que $\lim\limits_{z \to z_0} \dfrac{1}{f(z)} = 0$.
- Se deja como ejercicio al lector.
- Se deja como ejercicio al lector.
$\blacksquare$
La proposición 14.5 es de gran utilidad al trabajar con el punto al infinito. La idea de dicha proposición es representar al punto al infinito y su entorno mediante sus imágenes en la función $w = f(z) = 1/z$. Esto es, el punto $z=\infty$ corresponde con el punto $w=0$ y un $\varepsilon$-vecindario de $\infty$ corresponde con un $\varepsilon$-vecindario de $0$. Por lo que la existencia de un límite de una función $f(z)$ que considere al punto $z=\infty$ dependerá de la existencia de un límite que considere al punto $w=0$.
Ejemplo 14.6.
a) Consideremos a la función $f(z) = \dfrac{2z^3-1}{z^2+1}$ definida en $S=\mathbb{C}\setminus\{i,-i\}$. Veamos que: \begin{equation*} \lim_{z \to \infty} f(z) = \infty. \end{equation*} Solución. Notemos que: \begin{equation*} f(1/z) = \frac{(2/z^3)-1}{(1/z^2)+1}, \quad \quad \frac{1}{f(1/z)} = \frac{(1/z^2)+1}{(2/z^3)-1}. \end{equation*} De acuerdo con la proposición 14.5 como: \begin{equation*} \lim_{z \to 0} \frac{1}{f(1/z)} = \lim_{z \to 0} \frac{(1/z^2)+1}{(2/z^3)-1} = \lim_{z \to 0} \frac{z^3\left[(1/z^2)+1\right]}{z^3\left[(2/z^3)-1\right]} = \lim_{z \to 0} \frac{z^3 + z}{2 – z^3} = 0. \end{equation*} Entonces $\lim\limits_{z \to \infty} f(z) = \infty$.
b) Consideremos a la función $g(z) = \dfrac{iz+3}{z+1}$ con dominio $S=\mathbb{C}\setminus\{-1\}$. Veamos que: \begin{equation*} \lim_{z \to -1} g(z) = \infty. \end{equation*} Solución. Notemos que: \begin{equation*} \lim_{z \to -1} \frac{1}{g(z)} = \lim_{z \to -1} \frac{z+1}{iz+3} = 0. \end{equation*} Por lo que se sigue de la proposición 14.5 que $\lim\limits_{z \to \infty} g(z) = \infty$.
c) Sea $h(z) = \dfrac{2z+i}{z+1}$ una función definida en $S=\mathbb{C}\setminus\{-1\}$. Veamos que: \begin{equation*} \lim_{z \to \infty} h(z) = 2. \end{equation*} Solución. De acuerdo con la proposición 14.5 como: \begin{equation*} \lim_{z \to 0} h(1/z) = \lim_{z \to 0} \frac{(2/z)+i}{(1/z)+1} = \lim_{z \to 0} \frac{2+iz}{1 + z} = 2. \end{equation*} Entonces $\lim\limits_{z \to \infty} h(z) = 2$.
Tarea moral
- Completa la demostración de las proposiciones 14.3 y 14.5.
- Considera a la función $f(z) = \dfrac{zi}{2}$ definida en el disco abierto $B(0,1)$. Prueba usando la definición que: \begin{equation*} \lim_{z \to 1} f(z) = \frac{i}{2}. \end{equation*}
- Usando la definición de límite prueba que si: \begin{equation*} \lim_{z\to z_0} f(z) = w_0, \end{equation*} entonces: \begin{equation*} \lim_{z\to z_0} |\,f(z)\,| = |w_0|. \end{equation*} ¿Es cierto el recíproco?
- Considera la función $T:S\subset\mathbb{C}\to \mathbb{C}$ dada por: \begin{equation*} T(z) = \frac{az+b}{cz+b}, \quad \text{con} \,\, ad – bc \neq 0. \end{equation*} Usando la definición, prueba que:
a) Si $c=0$, entonces: \begin{equation*} \lim_{z \to \infty} T(z) = \infty. \end{equation*} b) Si $c\neq 0$, entonces: \begin{align*} \lim_{z \to \infty} T(z) = \frac{a}{c},\\ \lim_{z \to -\frac{d}{c}} T(z) = \infty. \end{align*} - Sean $a\in\mathbb{C}$ y $f,g\in\mathcal{F}(S)$ dos funciones. Considerando la definición 14.4 prueba las siguientes reglas para límites que consideran al punto al infinito.
a) Si $\lim\limits_{z\to z_0} f(z)=\infty$ y $\lim_{z\to z_0} g(z)=a$, entonces $\lim\limits_{z\to z_0}\left[ f(z) + g(z) \right]=\infty$.
b) Si $\lim\limits_{z\to z_0} f(z)=\infty$ y $\lim\limits_{z\to z_0} g(z)=a\neq 0$, entonces $\lim\limits_{z\to z_0}\left[ f(z) \cdot g(z) \right]=\infty$.
c) Si $\lim\limits_{z\to z_0} f(z)=\infty = \lim\limits_{z\to z_0} g(z)$, entonces $\lim\limits_{z\to z_0}\left[ f(z) \cdot g(z) \right]=\infty$.
d) Si $\lim\limits_{z\to z_0} f(z)=\infty$ y $\lim\limits_{z\to z_0} g(z)=a$, entonces $\lim\limits_{z\to z_0}\dfrac{g(z)}{f(z)}=0$.
e) Si $\lim\limits_{z\to z_0} f(z)=\infty$ y $\lim\limits_{z\to z_0} g(z)=a\neq 0$, entonces $\lim\limits_{z\to z_0}\dfrac{g(z)}{f(z)}=\infty$.
Más adelante…
En esta entrada hemos abordado de manera formal la definición de límite desde el enfoque de la variable compleja. Mediante una serie de resultados hemos caracterizado el límite complejo a través del estudio de la parte real e imaginaria de una función compleja, ya que dichas funciones reales las hemos estudiado a detalle en nuestros cursos de Cálculo, por lo que los resultados que conocemos para dichas funciones pueden emplearse al trabajar con funciones complejas.
Aunque las definiciones que hemos dado en esta entrada son idénticas a las de las funciones reales de variable real, veremos en las siguientes entradas que al trabajar con funciones complejas algunos conceptos se vuelven más restrictivos para estas funciones.
La siguiente entrada abordaremos un concepto fundamental en el estudio de las funciones complejas, el de continuidad, el cual estará ligado al concepto de límite, por lo que los resultados de esta entrada nos serán de utilidad.
Entradas relacionadas
- Ir a Variable Compleja I.
- Entrada anterior del curso: Funciones multivaludas.
- Siguiente entrada del curso: Continuidad en $\mathbb{C}$.