Introducción
Hasta ahora hemos visto que toda función compleja $f(z)$ diferenciable es continua, más aún sabemos que toda función compleja continua es de la forma: \begin{equation*} f(z) = u(x,y) + i v(x,y), \end{equation*} donde $u(x,y)$ y $v(x,y)$ son funciones reales continuas de variables $x,y$, por lo que resulta natural preguntarnos acerca de qué condiciones deben cumplir dichas funciones para que una función compleja $f(z)$ sea analítica. La respuesta a esta pregunta esta dada por las ecuaciones de Cauchy-Riemann, a las cuales nos referiremos simplemente como las ecuaciones de C-R. Dichas ecuaciones aparecieron por primera vez en 1821 en los primeros trabajos del matemático fránces Augustin Louis Cauchy sobre integrales de funciones complejas. Su relación con la existencia de la derivada compleja apareció hasta 1851 en la tesis doctoral del matemático alemán Bernhard Riemann.
Como veremos a lo largo de las siguientes entradas, las ecuaciones de C-R resultan ser un pilar en la teoría de las funciones complejas, por lo que nuestro objetivo será deducirlas y obtener una serie de resultados que nos permitan caracterizar a las funciones analíticas mediante dichas ecuaciones.
Recordemos las siguientes definiciones vistas en nuestros cursos de cálculo.
Definición 17.1. (Derivada parcial.)
Supongamos que $u: \mathbb{R}^2 \to \mathbb{R}$ es una función real de variables reales, $x,y$, definida en un conjunto abierto no vacío $U\subset \mathbb{R}^2$. Si consideramos a la variable $y$ como constante, entonces podemos pensar a $u$ como una función únicamente de $x$ y derivar con respecto a $x$. Entonces: \begin{equation*} \frac{\partial u }{\partial x}(x,y) = \lim_{h \to 0} \frac{u(x+h, y) – u(x,y)}{h}. \end{equation*}
En caso de existir dicho límite lo llamaremos la derivada parcial de $u$ con respecto a $x$ y es denotada como $\frac{\partial u }{\partial x}$ o $u_x$. Dicha derivada resulta ser una función evaluada en el punto $(x,y)$, lo cual se suele omitir por simplicidad en la notación.
Análogamente, fijando a $x$ y considerando a $u(x,y)$ como una función de $y$, tenemos al derivar con respecto a $y$ la derivada parcial de $u$ con respecto a $y$, es decir: \begin{equation*} \frac{\partial u }{\partial y}(x,y) = \lim_{h \to 0} \frac{u(x, y+h) – u(x,y)}{h}. \end{equation*}
Definición 17.2. (Funciones clase $C^k$.)
Si $U\subset\mathbb{R}^2$ es un conjunto abierto y $u:U\to\mathbb{R}$ es una función, entonces $u$ es llamada de clase $C^1$ o continuamente diferenciable en $U$ si $\partial u/\partial x$ y $\partial u/\partial y$ existen y son continuas en $U$. Lo anterior se denota de forma abreviada como $u\in C^1(U)$.
De forma general si $k\in\mathbb{N}$, entonces una función real $u$ definida en $U\subset\mathbb{R}^2$, es llamada de clase $C^k$ o $k$-veces continuamente diferenciable si todas las derivadas parciales hasta el orden $k$ existen y son continuas en $U$. En dicho caso escribimos $u\in C^k(U)$. En particular, diremos que una función $u$ es clase $C^0$ si simplemente es una función continua.
Entonces, para $U\subset \mathbb{C}$ abierto, una función $f(z) = u(x,y) + i v(x,y)$ definida en $U$, es llamada de clase $C^k$ si $u$ y $v$ son de clase $C^k$.
Observación 17.1.
A partir de ahora usaremos la notación $U$ para denotar conjuntos abiertos en $\mathbb{C}$ y $D$ para denotar dominios o regiones en $\mathbb{C}$, estos conceptos se abordaron en la Unidad 1: Introducción y preliminares.
De acuerdo con la observación 16.2 sabemos que si una función $f:U\to\mathbb{C}$ es diferenciable en un punto $z_0\in U$, entonces el límite: \begin{equation*} f'(z_0) = \lim_{z \to z_0} \dfrac{f(z) – f(z_0)}{z-z_0} = \lim_{h \to 0} \dfrac{f(z_0 + h) – f(z_0)}{h}, \end{equation*} existe y es único sin importar como $h$ se aproxime a $0$ en el plano complejo. Sin embargo es importante notar que al igual que en el caso de funciones reales, podemos considerar a dos direcciones privilegiadas cuando $h \to 0$, figura 73, las cuales son:
- a lo largo de un eje paralelo al eje real, es decir cuando $h\in \mathbb{R}$,
- a lo largo de un eje paralelo al eje imaginario, es decir cuando $h=ki\in\mathbb{C}$, con $k\in\mathbb{R}$, es un número complejo puro.
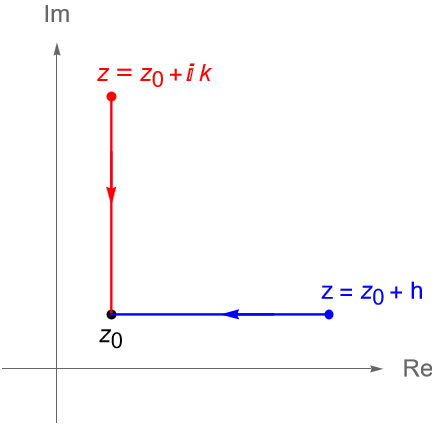
Veamos entonces qué sucede al calcular el límite que define a $f'(z)$ si consideramos las direcciones privilegiadas descritas previamente. Supongamos que $f(z) = u(x,y) + iv(x,y)$ es una función diferenciable en un punto $z_0=x_0+iy_0\in U$, con $U \subset \mathbb{C}$ abierto.
Si $h$ es real, entonces: \begin{align*} f'(z_0) &= \lim_{h \to 0} \frac{f(z_0+h) – f(z_0)}{h}\\ & = \lim_{h \to 0} \left[ \frac{u(x_0+h,y_0) – u(x_0,y_0)}{h} + i \frac{v(x_0+h,y_0) – v(x_0,y_0)}{h}\right]\\ & = \lim_{h \to 0} \frac{u(x_0+h,y_0) – u(x_0,y_0)}{h} + i \lim_{h \to 0} \frac{v(x_0+h,y_0) – v(x_0,y_0)}{h}\\ & = \frac{\partial u}{ \partial x}(x_0,y_0) + i \frac{\partial v}{ \partial x}(x_0,y_0)\\ & =: \frac{\partial f}{\partial x}(x_0,y_0) = f_x(z_0). \tag{17.1} \end{align*}
Si $h$ es un número imaginario puro, es decir $h=ik$, con $k$ real, entonces $h\to 0$ si y solo si $k\to 0$, por lo que: \begin{align*} f'(z_0) &= \lim_{h \to 0} \frac{f(z_0+h) – f(z_0)}{h}\\ & = \lim_{k \to 0} \left[ \frac{u(x_0,y_0+k) – u(x_0,y_0)}{ik} + i \frac{v(x_0,y_0+k) – v(x_0,y_0)}{ik}\right]\\ & = \frac{1}{i}\lim_{k \to 0} \frac{u(x_0,y_0+k) – u(x_0,y_0)}{k} + \lim_{k \to 0} \frac{v(x_0,y_0+k) – v(x_0,y_0)}{k}\\ & = -i \frac{\partial u}{ \partial y}(x_0,y_0) + \frac{\partial v}{ \partial y}(x_0,y_0)\\ & =: -i\frac{\partial f}{\partial y}(x_0,y_0) = -i f_y(z_0). \tag{17.2} \end{align*}
De ambos casos es claro que la existencia de las cuatro derivadas parciales: \begin{equation*} \frac{\partial u}{\partial x}, \quad \frac{\partial u}{\partial y}, \quad \frac{\partial v}{\partial x}, \quad \frac{\partial v}{\partial y} \end{equation*} en el punto $(x_0,y_0)$, está garantizada por la existencia del límite que define a la derivada compleja en el punto $z_0 = x_0 +iy_0 \in U$.
Observación 17.1.
Hemos introducido en las últimas igualdades de las ecuaciones (17.1) y (17.2) una notación usual en algunos textos para referirnos a la derivada de una función compleja en términos de las derivadas parciales de las funciones $u$ y $v$, es importante no confundirnos con dicha notación la cual se usará de manera indistinta en el curso.
Dado que $f'(z_0)$ existe sin importar la dirección en que $h$ se aproxime a $0$, entonces los dos límites dados en (17.1) y (17.2) deben ser iguales, es decir: \begin{equation*} f'(z_0) = \frac{\partial u}{ \partial x}(x_0,y_0) + i \frac{\partial v}{ \partial x}(x_0,y_0) = \frac{\partial v}{ \partial y}(x_0,y_0) -i \frac{\partial u}{ \partial y}(x_0,y_0), \tag{17.3} \end{equation*} o equivalentemente: \begin{equation*} f'(z_0) = f_x(z_0) = -i f_y(z_0). \tag{17.4} \end{equation*}
Igualando las partes reales e imaginarias de estos dos números complejos tenemos que: \begin{equation*} \frac{\partial u}{ \partial x} (x_0, y_0)= \frac{\partial v}{ \partial y}(x_0, y_0), \quad \text{y} \quad \frac{\partial u}{ \partial y}(x_0, y_0) = – \frac{\partial v}{ \partial x}(x_0, y_0). \tag{17.5} \end{equation*}
Al par de ecuaciones diferenciales parciales dado en (17.5) se les conoce como las ecuaciones de Cauchy-Riemann.
Con lo anterior hemos probado el siguiente resultado.
Teorema 17.1. (Ecuaciones de Cauchy-Riemann.)
Sean $U\subset \mathbb{C}$ un conjunto abierto y $f:U\to \mathbb{C}$ una función. Si $f(z) = u(x,y) + iv(x,y)$ es analítica en un punto $z_0=x_0 +iy_0\in U$, entonces existen las derivadas parciales: \begin{equation*} \frac{\partial u}{\partial x}, \quad \frac{\partial u}{\partial y}, \quad \frac{\partial v}{\partial x}, \quad \frac{\partial v}{\partial y} \end{equation*} en $(x_0,y_0)$ y satisfacen las ecuaciones de Cauchy-Riemann (17.5) en dicho punto. En tal caso se tiene que: \begin{equation*} f'(z_0) = \frac{\partial u}{\partial x}(x_0,y_0) + i \frac{\partial v}{\partial x}(x_0,y_0) = \frac{\partial v}{\partial y}(x_0,y_0) – i \frac{\partial u}{\partial y}(x_0,y_0). \end{equation*}
$\blacksquare$
Corolario 17.1.
Si $f(z)=u(x,y) + iv(x,y)$ es una función analítica en un conjunto abierto $U\subset\mathbb{C}$, entonces las ecuaciones de C-R se satisfacen en todo punto de $U$.
$\blacksquare$
De acuerdo con el corolario 16.1 de la entrada anterior, sabemos que todo polinomio complejo es una función entera, es decir, analítica en todo $\mathbb{C}$, por lo que de acuerdo con el corolario 17.1 se deben cumplir las ecuaciones de C-R para todo $z=x+iy\in\mathbb{C}$.
Ejemplo 17.1
Consideremos al polinomio complejo $f(z) = 2z^2 + 3z$, para $z=x+iy\in\mathbb{C}$, veamos que se satisfacen las ecuaciones de C-R en $\mathbb{C}$ y obtengamos la derivada de $f$.
Solución. Tenemos que: \begin{equation*} f(z) = 2(x^2 – y^2) + 3x + i(4xy + 3y), \end{equation*} de donde $u(x,y) = 2(x^2 – y^2) + 3x$ y $v(x,y) = 4xy + 3y$.
Entonces para todo $z=x+iy\in\mathbb{C}$ se satisfacen las ecuaciones de C-R: \begin{align*} \frac{\partial u}{\partial x} = 4x + 3 = \frac{\partial v}{\partial y},\\ \frac{\partial u}{\partial y} = -4y = – \frac{\partial v}{\partial x}. \end{align*}
Por otra parte, de acuerdo con el teorema 1 tenemos que la derivada de $f$ es: \begin{equation*} f'(z) = 4x+3 + i4y = 4(x+iy) + 3 = 4z + 3. \end{equation*}
Observación 17.3.
El teorema 17.1 establece que una condición necesaria para que una función $f(z)=u(x,y)+i v(x,y)$ sea analítica en un punto $z_0\in U \subset\mathbb{C}$ es que las ecuaciones de C-R se satisfagan en dicho punto.
La importancia del teorema 17.1 y del corolario 17.1 radica en que tenemos ahora un criterio para determinar cuando una función no es analítica por medio de las ecuaciones de C-R. Para mostrar esto consideremos los siguientes ejemplos.
Ejemplo 17.2.
De acuerdo con el ejemplo 16.3 de la entrada anterior, sabemos que las funciones $f(z) = \overline{z}$ y $g(z) = \operatorname{Re}(z)$ no son analíticas en ningún punto de $\mathbb{C}$. Utilizando la contrapuesta del corolario 17.1 procedemos a verificar nuestro resultado.
Solución. Es claro que ambas funciones están definidas en todo $\mathbb{C}$. Sea $z=x+iy\in\mathbb{C}$.
a) Para $f(z) = \overline{z} = x – iy$ tenemos que $u(x,y) = x$ y $v(x,y) = -y$, por lo que: \begin{align*} \frac{\partial u}{\partial x} = 1 \quad \text{y} \quad \frac{\partial u}{\partial y} = 0,\\ \frac{\partial v}{\partial x} = 0 \quad \text{y} \quad \frac{\partial v}{\partial y} = -1. \end{align*} Es claro que $\partial u/\partial x \neq \partial v/\partial y$ para todo $z = x+iy \in \mathbb{C}$, por lo que $f$ no es analítica en ningún punto.
b) Por otra parte, para $g(z) = \operatorname{Re}(z) = x$ tenemos que $u(x,y) = x$ y $v(x,y) = 0$, por lo que: \begin{align*} \frac{\partial u}{\partial x} = 1 \quad \text{y} \quad \frac{\partial u}{\partial y} = 0,\\ \frac{\partial v}{\partial x} = 0 \quad \text{y} \quad \frac{\partial v}{\partial y} = 0. \end{align*} Tenemos que $\partial u/\partial x \neq \partial v/\partial y$ y $\partial u/\partial y \neq -\partial v/\partial x$ para todo $z = x+iy \in \mathbb{C}$, por lo que $f$ no es analítica en ningún punto.
Ejemplo 17.3.
Sea $z=x+iy\in\mathbb{C}$. Veamos que la función compleja $f(z) = 2x^2 +y +i(y^2-x)$ no es analítica en ningún punto.
Solución. Notemos que $u(x,y) = 2x^2 + y$ y $v(x,y) = y^2 – x$, entonces: \begin{equation*} \frac{\partial u}{\partial x} = 4x \quad \text{y} \quad \frac{\partial u}{\partial y} = 1, \end{equation*} \begin{equation*} \frac{\partial v}{\partial x} = -1 \quad \text{y} \quad \frac{\partial v}{\partial y} = 2y. \end{equation*}
Es claro que $\partial u/\partial y = -\partial v/\partial x$ para todo $z=x+iy \in \mathbb{C}$, mientras que la igualdad $\partial u/\partial x = \partial v/\partial y$ se satisface solamente en la recta $y=2x$. Sin embargo, para todo punto $z=x+iy$ sobre dicha recta, no existe un disco abierto alrededor de $z$ en el cual $f$ sea diferenciable, por lo que $f$ no es analítica en ningún punto.
Es importante notar que aunque se satisfagan las ecuaciones de C-R en un punto $z_0= x_0+iy_0\in D$, esto no es suficiente para garantizar la existencia de $f'(z_0)$ en $D$, desde que existen muchas otras direcciones por las que $z$ se aproxima a $z_0$ al calcular el límite que define a $f'(z_0)$. Consideremos el siguiente ejemplo para verificar lo anterior.
Ejemplo 17.4.
Sea $z=x+iy$. Veamos que la función: \begin{equation*} f(z)= \left\{\begin{array}{lcc} \dfrac{x^3(1+i) – y^3(1-i)}{x^2+y^2}& \text{si} & z\neq 0, \\ 0 & \text{si} & z = 0, \end{array} \right. \end{equation*} es continua en $z=0$ y que en dicho punto se satisfacen las ecuaciones de C-R, pero $f'(0)$ no existe.
Solución. Sea $f(z)=u(z)+iv(z)$, entonces para $z\neq 0$ tenemos que: \begin{equation*} u(x,y) = \frac{x^3 – y^3}{x^2+y^2}, \quad v(x,y) = \frac{x^3 + y^3}{x^2+y^2}, \end{equation*} con $x\neq 0$ y $y\neq 0$.
Primeramente verifiquemos que $f(z)$ es continua en todo $\mathbb{C}$. Es claro que si $z\neq 0$, entonces las funciones racionales $u(x,y)$ y $v(x,y)$ están bien definidas y son continuas, por lo que en dicho caso $f(z)$ es continua. Probemos ahora que $f(z)$ es continua en $z=0$. Utilizando coordenadas polares tenemos que: \begin{equation*} u(r,\theta) = r\left(\operatorname{cos}^3(\theta) – \operatorname{sen}^3(\theta)\right), \quad v(r,\theta) = r\left(\operatorname{cos}^3(\theta) + \operatorname{sen}^3(\theta)\right). \end{equation*}
Notemos que si $z\to 0$, entonces $r \to 0$, para cualquier argumento $\theta$, por lo que: \begin{equation*} \lim_{r \to 0} u(r,\theta) = \lim_{r \to 0} v(r,\theta) = 0, \end{equation*} entonces: \begin{equation*} \lim_{z \to 0} f(z) = 0 = f(0), \end{equation*} por lo que $f(z)$ es continua en $z=0$ y por tanto es continua en todo $\mathbb{C}$.
Veamos ahora que en $z=0$ las ecuaciones de C-R se satisfacen. Si $z=0$, entonces: \begin{align*} f(0) = 0 \quad & \Longleftrightarrow \quad u(0,0) + iv(0,0) = 0\\ & \Longleftrightarrow \quad u(0,0) = v(0,0) = 0. \end{align*} Por definición tenemos que: \begin{align*} \frac{\partial u}{\partial x} (0,0) & = \lim_{h\to 0}\frac{u(h,0) – u(0,0)}{h}\\ & = \lim_{h\to 0}\frac{h – 0}{h}\\ & = 1. \end{align*} \begin{align*} \frac{\partial u}{\partial y} (0,0) & = \lim_{h\to 0}\frac{u(0,h) – u(0,0)}{h}\\ & = \lim_{h\to 0}\frac{-h – 0}{h}\\ & = -1. \end{align*} Mientras que: \begin{align*} \frac{\partial v}{\partial x} (0,0) & = \lim_{h\to 0}\frac{v(h,0) – v(0,0)}{h}\\ & = \lim_{h\to 0}\frac{h – 0}{h}\\ & = 1. \end{align*} \begin{align*} \frac{\partial v}{\partial y} (0,0) & = \lim_{h\to 0}\frac{v(0,h) – v(0,0)}{h}\\ & = \lim_{h\to 0}\frac{h – 0}{h}\\ & = 1. \end{align*} Entonces, en el origen tenemos que: \begin{equation*} \frac{\partial u}{ \partial x} = \frac{\partial v}{ \partial y}, \quad \frac{\partial v}{ \partial x} = -\frac{\partial u}{ \partial y}, \end{equation*} por lo que en $z=0$ se satisfacen las ecuaciones de C-R. Sin embargo, $f(z)$ no es diferenciable en dicho punto.
Para $z=x+iy$ tenemos que: \begin{align*} f'(0) & = \lim_{z \to 0} \frac{f(z) – f(0)}{z}\\ & = \lim_{z \to 0} \frac{f(z) – 0}{z}\\ & = \lim\limits_{\begin{subarray}{l} x \to 0\\ y \to 0 \end{subarray}} \frac{(x^3 – y^3) + i (x^3 + y^3)}{(x^2+y^2)(x+iy)}. \end{align*} Notemos que si $z$ se aproxima $0$ a lo largo de la recta $y=x$, entonces: \begin{align*} f'(0) & = \lim_{z \to 0} \frac{f(z) – f(0)}{z}\\ & = \lim_{x \to 0} \frac{2ix^3}{2x^3(1+i)}\\ & = \frac{i}{1+i}. \end{align*} Por otra parte, si $z$ se aproxima $0$ a lo largo del eje real $x$, es decir si $y=0$, entonces: \begin{align*} f'(0) & = \lim_{z \to 0} \frac{f(z) – f(0)}{z}\\ & = \lim_{x \to 0} \frac{x^3(1+i)}{x^3}\\ & = 1+i. \end{align*} Dado que estos límites son distintos, entonces $f'(0)$ no existe y por tanto $f(z)$ no es diferenciable en $z=0$.
De acuerdo con la proposición 16.1 de la entrada anterior, sabemos que una consencuencia de la analicidad de una función $f$ en un punto $z_0 \in U\subset\mathbb{C}$, es la continuidad de la función $f$ en dicho punto. Sin embargo, el ejemplo 17.4 muestra que el recíproco de dicha proposición no es cierto, pues la función $f(z)$ de dicho ejemplo es continua en $z_0 = 0$, pero no es analítica en dicho punto.
Observación 17.4.
De nuestros cursos de geometría sabemos que al trabajar con coordenadas polares es posible establecer una transformación biunívoca entre las coordenadas polares y las coordenadas cartesianas mediante la transformación: \begin{align*} T: (0,\infty) \times (-\pi,\pi] \to \mathbb{R}^2\setminus\{(0,0)\},\\ T(r,\theta)=(r\operatorname{cos}(\theta), r\operatorname{sen}(\theta)). \end{align*} Por ejemplo, para el conjunto de puntos: \begin{equation*} U^* = \left\{(r,\theta) : 1\leq r \leq 2 \, \, \text{y} \,\, 0\leq \theta \leq \pi/2\right\}, \end{equation*} se tiene que $T(U^*) = U$, con: \begin{equation*} U = \left\{(x,y) : 1/2 \leq x \leq 1 \, \, \text{y} \,\, \sqrt{1-x^2} \leq y \leq \sqrt{3} x \right\}\cup \left\{(x,y) : 1 \leq x \leq 2 \, \, \text{y} \,\, 0 \leq y \leq \sqrt{4-x^2}\right\}. \end{equation*}
De acuerdo con la observación 12.5, al considerar a $z\in\mathbb{C}$, $z\neq 0$, en su forma polar, es posible expresar a una función compleja $f(z)$ en términos de su parte real e imaginaria, las cuales son funciones reales de las variables $r$ y $\theta$, por lo que considerando la transformación anterior, resulta sencillo verificar el siguiente resultado.
Proposición 17.1. (Forma polar de las ecuaciones de C-R.)
Sean $U\subset\mathbb{C}\setminus{0}$ un conjunto abierto y $f\in\mathcal{F}(U)$ una función. Si la función $f(z)=u(x,y) + iv(x,y)$ es analítica en $U$, entonces considerando la transformación dada por $x=r\operatorname{cos}(\theta)$, $y=r\operatorname{sen}(\theta)$, para $(r,\theta)\in U^*$ y $U^* \subset (0,\infty)\times(-\pi, \pi]$, se tiene que las ecuaciones de Cauchy-Riemann en su forma polar están dadas por: \begin{equation*} \frac{\partial u}{\partial r} = \frac{1}{r} \frac{\partial v}{\partial \theta} \quad \text{y} \quad \frac{\partial v}{\partial r} = -\frac{1}{r} \frac{\partial u}{\partial \theta}, \tag{17.6} \end{equation*} las cuales existen para cada punto de $U$.
Más aún, en consecuencia con el teorema 1, se tiene que para $z_0 = r_0 \operatorname{cis}(\theta_0) \in U$, un punto donde $f$ es analítica, se cumple que: \begin{align*} f'(z_0) & = \operatorname{cis}(-\theta) \left[ \frac{\partial u}{\partial r} (r_0, \theta_0)+ i \frac{\partial v}{\partial r}(r_0, \theta_0)\right]\\ & = \left[\operatorname{cos}(\theta) – i \operatorname{sen}(\theta) \right]\left[ u_r(r_0, \theta_0)+ i v_r(r_0, \theta_0)\right]. \end{align*}
Demostración. Se deja como ejercicio al lector.
$\blacksquare$
Ejemplo 17.5.
Consideremos a la función $f(z) = \dfrac{1}{z^2}$. De acuerdo con el corolario 16.1 sabemos que dicha función es analítica en $\mathbb{C}\setminus\{0\}$, por lo que considerando a $z\neq 0$ en coordenadas polares podemos verificar que se cumplen las ecuaciones de C-R en su forma polar para todo $(r,\theta) \in (0,\infty) \times (-\pi,\pi]$ o equivalentemente, por la observación 17.4, para todo $z \in \mathbb{C}\setminus\{0\}$.
Solución.
Sea $z=r\operatorname{cis}(\theta) \neq 0$, con $r = |\,z\,|$ y $\theta = \operatorname{Arg} z$. Por la fórmula de De Moivre tenemos que: \begin{align*} f(z) = \frac{1}{z^2} & = \frac{1}{\left[r\operatorname{cis}(\theta)\right]^2}\\ & = \frac{1}{r^2\left[\operatorname{cos}(2\theta) + \operatorname{sen}(2\theta)\right]}\\ & = \frac{\operatorname{cos}(2\theta) – i \operatorname{sen}(2\theta)}{r^2}\\ & = \frac{\operatorname{cos}(2\theta)}{r^2} – i \frac{\operatorname{sen}(2\theta)}{r^2}. \end{align*} Entonces: \begin{align*} u(r,\theta) = \frac{\operatorname{cos}(2\theta)}{r^2},\\ v(r,\theta) = – \frac{\operatorname{sen}(2\theta)}{r^2}. \end{align*} Tenemos que para todo $(r,\theta)\in(0,\infty)\times (-\pi,\pi]$ se cumple que: \begin{align*} \frac{\partial u}{\partial r} = – \frac{2\operatorname{cos}(\theta)}{r^3} = \frac{1}{r} \frac{\partial v}{\partial \theta},\\ \frac{\partial v}{\partial r} = \frac{2\operatorname{sen}(\theta)}{r^3} = -\frac{1}{r} \frac{\partial u}{\partial \theta}. \end{align*} Por lo tanto, para todo $z=r\operatorname{cis}(\theta) \in \mathbb{C}\setminus\{0\}$ se satisfacen las ecuaciones de C-R.
Es claro que utilizando las reglas de derivación vistas en la entrada anterior es posible obtener la derivada de $f$ para todo $z\neq 0$, sin embargo utilizando la proposición 17.1 tenemos que: \begin{align*} f'(z) & = \operatorname{cis}(-\theta) \left[ \frac{\partial u}{\partial r}+ i \frac{\partial v}{\partial r}\right]\\ & = \left[\operatorname{cos}(\theta) – i \operatorname{sen}(\theta) \right]\left[ – \frac{2\operatorname{cos}(\theta)}{r^3} + i \frac{2\operatorname{sen}(\theta)}{r^3}\right]\\ & = – \frac{2}{r^3} \left[ \left( \operatorname{cos}^3(\theta) -3\operatorname{sen}^2(\theta) \operatorname{cos}(\theta)\right) – i \left( 3\operatorname{cos}^2(\theta) \operatorname{sen}(\theta) – \operatorname{sen}^3(\theta) \right)\right]\\ & = – \frac{2}{r^3} \left[ \operatorname{cos}(-3\theta) + i \operatorname{sen}(-3\theta)\right]\\ & = – \frac{2}{r^3 \operatorname{cis}(3\theta)}\\ & = – \frac{2}{\left( r \operatorname{cis}(\theta)\right)^3} = – \frac{2}{z^3}. \end{align*}
Ejemplo 17.6.
De acuerdo con el ejemplo 16.5 sabemos que $f_0$, es decir la rama principal de la función multivaluada $F(z)=\sqrt{z}$, es analítica en el dominio $D=\mathbb{C}\setminus(-\infty,0]$. Veamos que se cumplen las ecuaciones de C-R en $D$.
Solución. Sea $z\in D$. Escribiendo $z = r\operatorname{cis}(\theta)$, con $r=|\,z\,|$ y $\theta =\operatorname{Arg}(z)$, entonces: \begin{align*} f_0(z) & = \sqrt{r}\operatorname{cis}\left(\frac{\theta}{2}\right)\\ & = \sqrt{r}\operatorname{cos}\left(\frac{\theta}{2}\right) + i \sqrt{r}\operatorname{sen}\left(\frac{\theta}{2}\right)\\ & = u(r,\theta) + iv(r,\theta). \end{align*}
Es claro que para todo $(r,\theta)\in(0,\infty)\times (-\pi,\pi)$ se cumple que: \begin{align*} \frac{\partial u}{\partial r} = \frac{\operatorname{cos}\left(\frac{\theta}{2}\right)}{2\sqrt{r}} = \frac{1}{r} \frac{\partial v}{\partial \theta},\\ \frac{\partial v}{\partial r} = \frac{\operatorname{sen}\left(\frac{\theta}{2}\right)}{2\sqrt{2}} = -\frac{1}{r} \frac{\partial u}{\partial \theta}. \end{align*}
Por lo que para todo $z = r\operatorname{cis}(\theta)\in D$ se cumplen las ecuaciones de C-R.
Tarea moral
- Demuestra la proposición 17.1.
Hint: Observa que $u(x,y) = u(r\operatorname{cos}(\theta), r\operatorname{sen}(\theta))$ y $v(x,y) = v(r\operatorname{cos}(\theta), r\operatorname{sen}(\theta))$. Dado que la función $f$ es analítica en el abierto $U$, por el corolario 1 se satisfacen las ecuaciones de C-R en $U$, por lo que utilizando la regla de la cadena para funciones reales de dos variables se tiene que: \begin{align*} \frac{\partial u}{\partial r} = \frac{\partial u}{\partial x} \frac{\partial x}{\partial r} + \frac{\partial u}{\partial y} \frac{\partial y}{\partial r}, \quad \frac{\partial u}{\partial \theta} = \frac{\partial u}{\partial x} \frac{\partial x}{\partial \theta} + \frac{\partial u}{\partial y} \frac{\partial y}{\partial \theta},\\ \frac{\partial v}{\partial r} = \frac{\partial v}{\partial x} \frac{\partial x}{\partial r} + \frac{\partial v}{\partial y} \frac{\partial y}{\partial r}, \quad \frac{\partial v}{\partial \theta} = \frac{\partial v}{\partial x} \frac{\partial x}{\partial \theta} + \frac{\partial v}{\partial y} \frac{\partial y}{\partial \theta}. \tag{17.7} \end{align*} - De las ecuaciones dadas en (17.7), resuelve para $u_x$, $u_y$, $v_x$ y $v_y$ y concluye que: \begin{align*} \frac{\partial u}{\partial x} = \frac{\partial u}{\partial r} \operatorname{cos}(\theta) – \frac{\partial u}{\partial \theta} \frac{\operatorname{sen(\theta)}}{r}, \quad \frac{\partial u}{\partial y} = \frac{\partial u}{\partial r} \operatorname{sen}(\theta) + \frac{\partial u}{\partial \theta}\frac{\operatorname{cos(\theta)}}{r},\\ \frac{\partial v}{\partial x} = \frac{\partial v}{\partial r} \operatorname{cos}(\theta) – \frac{\partial v}{\partial \theta} \frac{\operatorname{sen(\theta)}}{r}, \quad \frac{\partial v}{\partial y} = \frac{\partial v}{\partial r} \operatorname{sen}(\theta) + \frac{\partial v}{\partial \theta}\frac{\operatorname{cos(\theta)}}{r}. \end{align*} Suponiendo que el teorema 1 se cumple para la forma polar de las ecuaciones de C-R, utiliza las ecuaciones anteriores para verificar que las ecuaciones de C-R se verifican ahora para las funciones reales $u(x,y)$ y $v(x,y)$. Con esto se verifica que las ecuaciones dadas en (17.6) en efecto son la forma polar de las ecuaciones de C-R.
- Prueba que las siguientes funciónes no son analíticas en su dominio.
a) $f(z) = |\,z\,|^2$, pero es diferenciable en $z=0$.
b) $f(z) = y + ix$, para $z=x+iy\in\mathbb{C}$.
c) $f(z) = \overline{z}^2$ para $z=x+iy\in\mathbb{C}$.
d) $f(z) = 4z – 6 \overline{z} + 3$ para $z=x+iy\in\mathbb{C}$. - Supón que $f(z) = u(x,y) + iv(x,y)$ es una función analítica en un conjunto abierto $U\subset\mathbb{C}$. Sean $h(z) = \overline{f(z)}$ y $g(z) = v(x,y) + iu(x,y)$ dos funciones complejas definidas en el mismo conjunto $U$, entonces ¿son $h$ y $g$ funciones analíticas en $U$?
- Sean $U\subset\mathbb{C}$ un conjunto abierto y $f(z) = u(x,y) + iv(x,y)$ una función analítica en un $U$. Prueba que:
a) $f'(z) = u_x(z) – i u_y(z) = v_y(z) + i v_x(z)$.
b) $|\,f'(z)\,|^2 = u_x^2 + u_y^2 = v_x^2 + v_y^2$, para todo $z=x+iy\in U$. - Considera la siguiente función: \begin{equation*} f(z)= \left\{\begin{array}{lcc} \dfrac{z^5}{|\,z\,|^4}& \text{si} & z\neq 0, \\ 0 & \text{si} & z = 0. \end{array} \right. \end{equation*} Muestra que en $z=0$ la función $f$ satisface las ecuaciones de C-R, pero $f'(0)$ no existe.
Más adelante…
En esta entrada hemos deducido las ecuaciones de Cauchy-Riemann y probamos que para una función compleja $f(z) = u(x,y) + iv(x,y)$ dichas ecuaciones resultan ser un conjunto de condiciones necesarias que deben satisfacer la parte real y la parte imaginaria, $u$ y $v$ respectivamente, en un punto donde $f(z)$ es analítica. Sin embargo, vimos mediante algunos ejemplos que dichas ecuaciones no son una condición suficiente para garantizar la analicidad de una función en un conjunto abierto $U\subset\mathbb{C}$.
Lo anterior nos motiva a preguntarnos bajo qué condiciones, además de las ecuaciones de C-R, las funciones reales $u$ y $v$ nos permiten garantizar que una función compleja $f(z)$ sea analítica en $U$, lo cual responderemos en la siguiente entrada.
Entradas relacionadas
- Ir a Variable Compleja I.
- Entrada anterior del curso: Diferenciabilidad en el sentido complejo.
- Siguiente entrada del curso: Ecuaciones de Cauchy-Riemann. Condiciones suficientes para la diferenciabilidad compleja.

Buenisimo el aporte, muchas gracias <3
Gracias también a ti por el comentario, Jessica. Esperamos que sigas disfrutando de nuestro material.