Archivo del Autor: Eduardo Vera Rosales

Ecuaciones Diferenciales I – Videos: Plano fase para sistemas lineales con valores propios complejos

Por Eduardo Vera Rosales

Deja un comentario

Introducción

En la entrada anterior comenzamos a estudiar el plano fase para sistemas de dos ecuaciones homogéneas con coeficientes constantes de la forma $$\begin{pmatrix} \dot{x} \\ \dot{y} \end{pmatrix}=\begin{pmatrix} a & b \\ c & d \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix}.$$ En particular, revisamos el caso cuando los valores propios del sistema son reales distintos y no son cero. Vimos que el comportamiento de las curvas y la estabilidad del punto de equilibrio dependen del signo de los valores propios. Así, cuando los signos difieren tenemos un punto silla (inestable), cuando los dos valores propios son negativos tenemos un atractor (punto de equilibrio asintóticamente estable) y finalmente, cuando ambos valores propios son positivos el punto de equilibrio es un repulsor (inestable).

Es turno ahora de analizar el plano fase para sistemas cuyos valores propios son complejos. Sabemos que si $\lambda_{1}=\alpha + \beta i$ es un valor propio del sistema, entonces su conjugado $\lambda_{2}=\alpha – \beta i$ también es un valor propio. Además la solución general a dichos sistemas tiene la forma $$\textbf{X}(t)=c_{1}e^{\alpha t}\left(\cos{\beta t}\begin{pmatrix} u_{1} \\ u_{2} \end{pmatrix}-\sin{\beta t}\begin{pmatrix} v_{1} \\ v_{2} \end{pmatrix}\right)+c_{2}e^{\alpha t}\left(\sin{\beta t} \begin{pmatrix} u_{1} \\ u_{2} \end{pmatrix}+\cos{\beta t} \begin{pmatrix} v_{1} \\ v_{2} \end{pmatrix}\right)$$ donde los vectores $(u_{1},u_{2})$ y $(v_{1},v_{2})$ son vectores tales que $$\textbf{w}=(u_{1},u_{2})+i(v_{1},v_{2})$$ es un vector propio para $\lambda_{1}$.

Estudiaremos las soluciones cuando $t \rightarrow \infty$. La forma del plano fase va a depender de la parte real $\alpha$ de los valores propios (nota que los dos valores propios tienen la misma parte real), por lo que distinguiremos tres casos, según $\alpha$ sea positivo, negativo o cero. Finalmente clasificaremos a los puntos de equilibrio según su estabilidad.

Plano fase para sistemas con valores propios complejos

En el primer video estudiamos de manera general el plano fase para sistemas de la forma $$\begin{pmatrix} \dot{x} \\ \dot{y} \end{pmatrix}=\begin{pmatrix} a & b \\ c & d \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix}$$ cuyos valores propios son complejos. Analizamos tres casos: cuando la parte real de los valores propios es positiva, negativa o cero.

En el segundo video resolvemos y dibujamos el plano fase para distintos sistemas con valores propios complejos.

Tarea moral

Los siguientes ejercicios no forman parte de la evaluación del curso, pero te servirán para entender mucho mejor los conceptos vistos en esta entrada, así como temas posteriores.

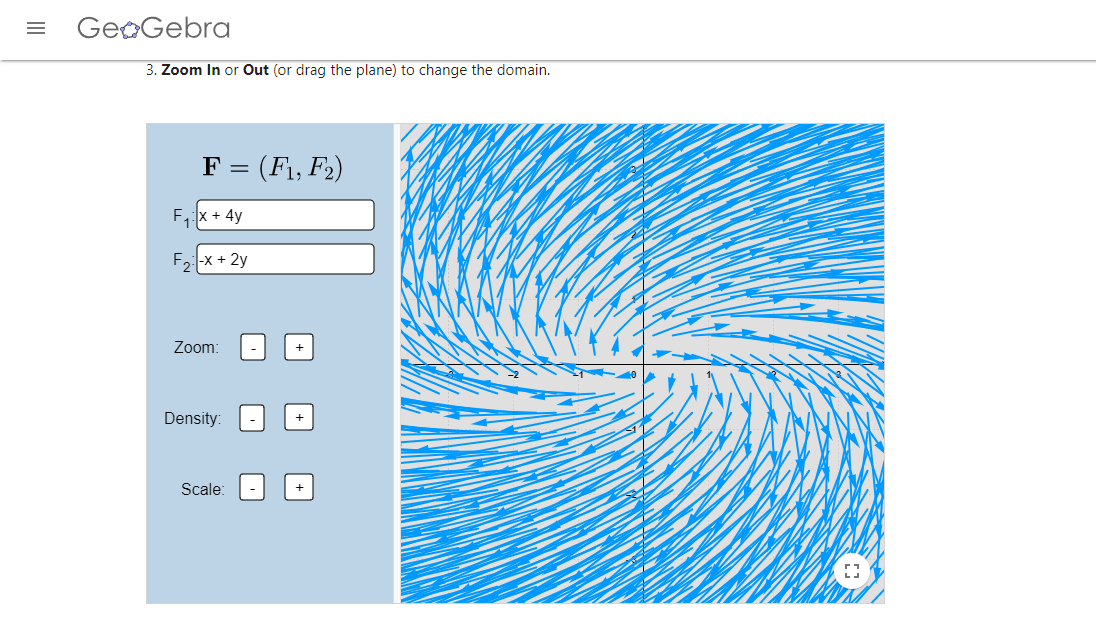
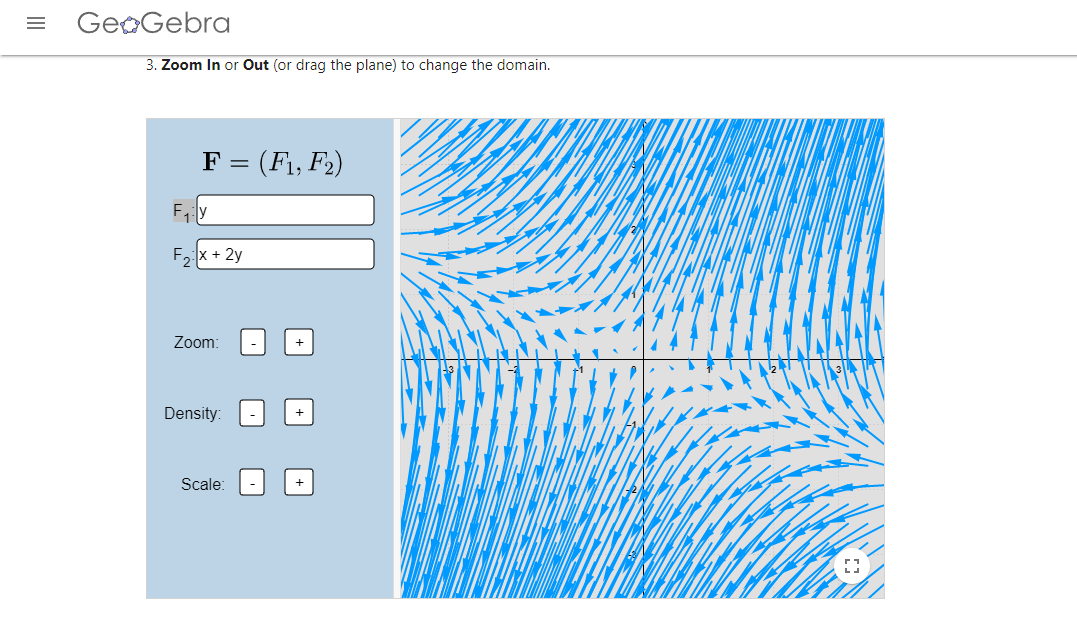
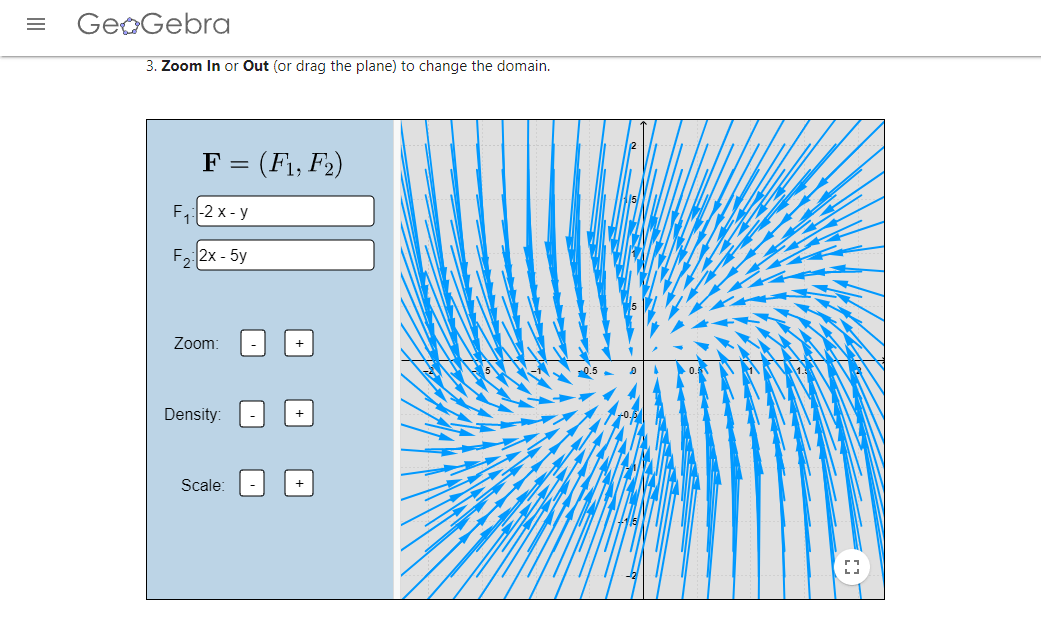
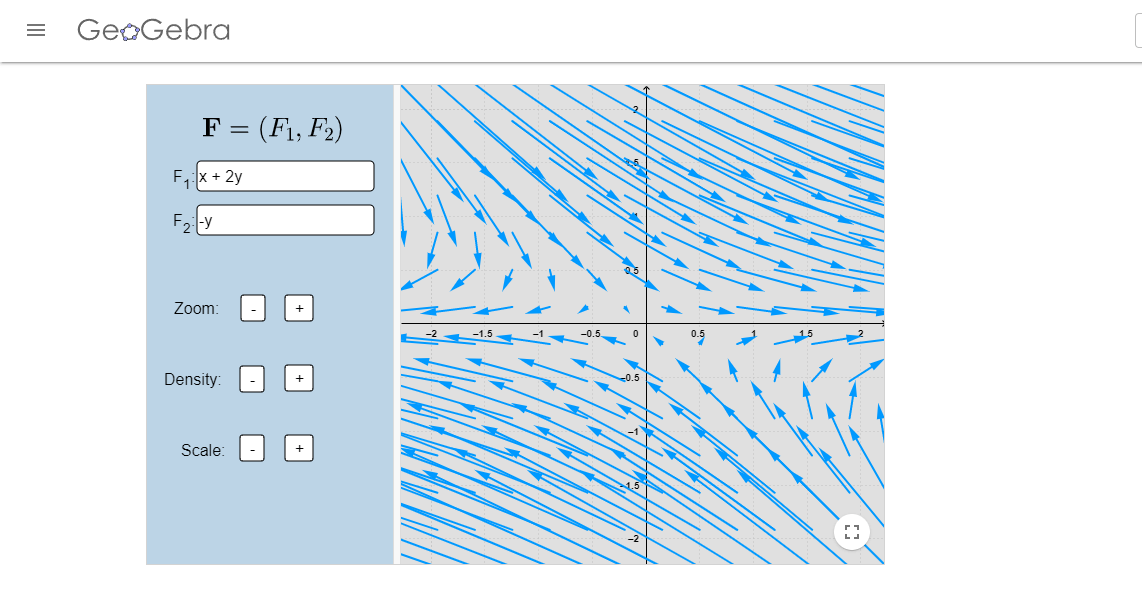
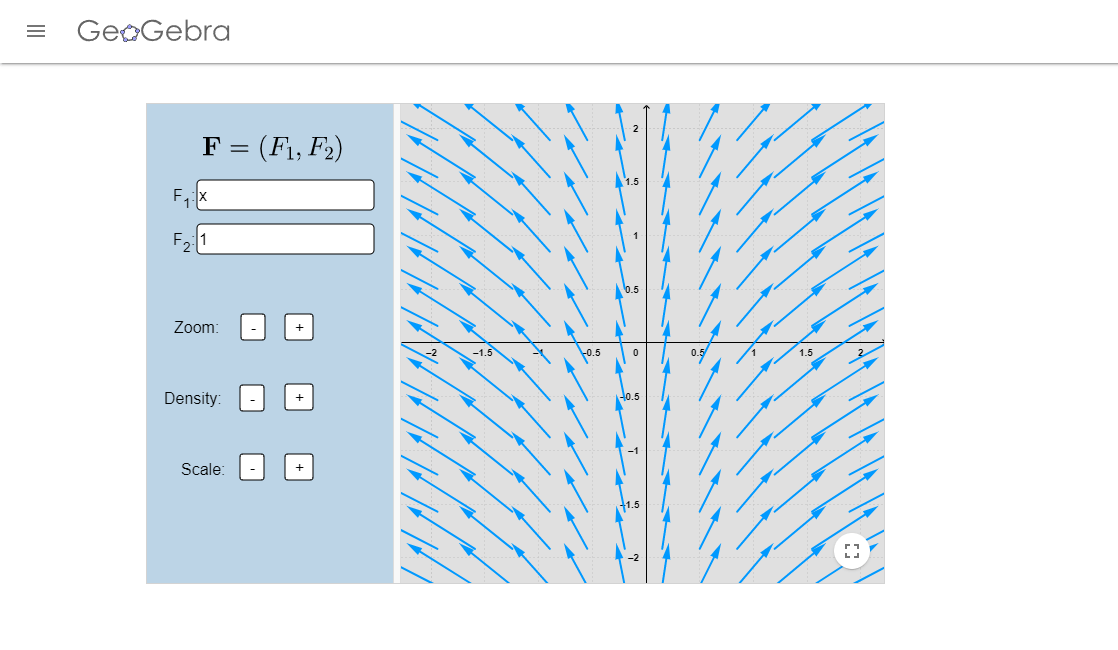
Los campos vectoriales de las imágenes fueron realizados en el siguiente enlace.

  • Prueba que la función $$\textbf{X}(t)=\begin{pmatrix} (c_{1}u_{1}+c_{2}v_{1})\cos{\beta t}+(c_{2}u_{1}-c_{1}v_{1})\sin{\beta t} \\ (c_{1}u_{2}+c_{2}v_{2})\cos{\beta t}+(c_{2}u_{2}-c_{1}v_{2})\sin{\beta t} \end{pmatrix}$$ es periódica, con período $\frac{2\pi}{\beta}$, donde $c_{1},c_{2},u_{1},u_{2},v_{1},v_{2}$ son valores constantes.
  • De acuerdo al ejercicio anterior, concluye que si un sistema homogéneo con coeficientes constantes tiene un valor propio complejo $\lambda_{1}=\beta i$ con vector propio asociado $\textbf{w}=(u_{1},u_{2})+i(v_{1},v_{2})$, entonces las curvas en el plano fase son cerradas.
  • Considera ahora la función $$\textbf{X}(t)=e^{\alpha t}\begin{pmatrix} (c_{1}u_{1}+c_{2}v_{1})\cos{\beta t}+(c_{2}u_{1}-c_{1}v_{1})\sin{\beta t} \\ (c_{1}u_{2}+c_{2}v_{2})\cos{\beta t}+(c_{2}u_{2}-c_{1}v_{2})\sin{\beta t} \end{pmatrix}$$ con $\alpha \neq 0$. Prueba que los puntos en el plano que son imagen de valores periódicos bajo la función del primer ejercicio se quedan contenidos en una recta. Concluye el comportamiento espiral de las soluciones a sistemas de ecuaciones con valores complejos cuya parte real es distinta de cero.
  • Prueba que el punto de equilibrio del sistema $$\begin{pmatrix} \dot{x} \\ \dot{y} \end{pmatrix}=\begin{pmatrix} 0 & b \\ -b & 0 \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix}$$ es un centro.
  • Resuelve y dibuja el plano fase del sistema $$\begin{pmatrix} \dot{x} \\ \dot{y} \end{pmatrix}=\begin{pmatrix} 2 & 1 \\ -2 & 0 \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix}.$$
  • Encuentra la solución general y dibuja el plano fase del sistema $$\begin{pmatrix} \dot{x} \\ \dot{y} \end{pmatrix}=\begin{pmatrix} 0 & 1 \\ -1 & -1 \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix}.$$
  • Dibuja el plano fase del sistema $$\begin{pmatrix} \dot{x} \\ \dot{y} \end{pmatrix}=\begin{pmatrix} 0 & 1 \\ -5 & 0 \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix}.$$

(Recuerda que puedes apoyarte del campo vectorial asociado para dibujar el plano fase).

Más adelante

Seguimos avanzando en el estudio del plano fase para sistemas homogéneos con coeficientes constantes. Ya sabemos la forma de las soluciones para sistemas cuyos valores propios son reales distintos y no nulos, o complejos. En la próxima entrada continuaremos revisando el plano fase, pero ahora para sistemas que tienen valores propios repetidos.

¡Hasta la próxima!

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Ecuaciones Diferenciales I – Videos: Plano fase para sistemas lineales con valores propios reales distintos no nulos

Por Eduardo Vera Rosales

Deja un comentario

Introducción

En las dos entradas anteriores revisamos los conceptos esenciales para poder estudiar el plano fase del sistema de ecuaciones de primer orden homogéneas con coeficientes constantes $$\begin{pmatrix} \dot{x} \\ \dot{y} \end{pmatrix}=\begin{pmatrix} a & b \\ c & d \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix}.$$ Revisamos el campo vectorial asociado al sistema, que para los sistemas que estamos considerando se reduce al campo $\textbf{F}(x,y)=(ax+by, cx+dy)$. A cada $(x,y)$, el campo asocia un vector anclado en dicho punto, que además será tangente a las curvas solución. Si observamos el campo vectorial en el plano, entonces podemos darnos una idea aproximada de cómo se verían las curvas solución, y por tanto, el plano fase completo. Por otra parte estudiamos la estabilidad de los puntos de equilibrio, que son aquellos donde el campo vectorial se anula, es decir, cuando $\textbf{F}(x,y)=(0,0)$. De ellos depende el comportamiento del resto de las soluciones en el plano fase.

Con estos ingredientes, estamos listos para poder dibujar los planos fase de casi cualquier sistema de dos ecuaciones con coeficientes constantes. Como sabemos, la solución general a estos sistemas depende de los valores propios de la matriz asociada. Analizaremos el comportamiento de dichas soluciones, comenzando en esta entrada con el caso cuando los valores propios del sistema son reales distintos y no nulos. Después de cada análisis podremos hacer un dibujo esquemático de cómo se ven las soluciones en el plano fase.

¡Vamos a comenzar!

Plano fase para sistemas con valores propios reales distintos no nulos

En el primer video analizamos de manera general el comportamiento de las soluciones a sistemas de la forma $$\begin{pmatrix} \dot{x} \\ \dot{y} \end{pmatrix}=\begin{pmatrix} a & b \\ c & d \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix}$$ cuando estos tienen valores propios reales distintos y no nulos. Dependiendo del signo de los valores propios será la forma del plano fase.

En el segundo video resolvemos un ejemplo por cada caso analizado en el video anterior.

Tarea moral

Los siguientes ejercicios no forman parte de la evaluación del curso, pero te servirán para entender mucho mejor los conceptos vistos en esta entrada, así como temas posteriores.

Los campos vectoriales de las imágenes fueron realizados en el siguiente enlace.

  • Considera el sistema de ecuaciones $$\begin{pmatrix} \dot{x} \\ \dot{y} \end{pmatrix}=\begin{pmatrix} a & b \\ c & d \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix}.$$ Prueba que si el determinante de la matriz asociada es cero, entonces el sistema tiene al menos un valor propio $\lambda=0$.
  • Dibuja el plano fase del sistema $$\begin{pmatrix} \dot{x} \\ \dot{y} \end{pmatrix}=\begin{pmatrix} 1 & 1 \\ 4 & 1 \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix}.$$
  • Encuentra la solución general al sistema y dibuja su plano fase: $$\begin{pmatrix} \dot{x} \\ \dot{y} \end{pmatrix}=\begin{pmatrix} 5 & -1 \\ 3 & 1 \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix}.$$ Posteriormente grafica la curva correspondiente a la condición inicial $$\textbf{X}(0)=\begin{pmatrix} 2 \\ 1 \end{pmatrix}.$$
  • Dibuja el plano fase del sistema $$\begin{pmatrix} \dot{x} \\ \dot{y} \end{pmatrix}=\begin{pmatrix} 1 & 1 \\ 2 & 3 \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix}.$$
  • Relaciona cada sistema de ecuaciones con la imagen correspondiente a su plano fase:
  1. $$\begin{pmatrix} \dot{x} \\ \dot{y} \end{pmatrix}=\begin{pmatrix} 3 & -2 \\ 2 & -2 \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix}.$$
  2. $$\begin{pmatrix} \dot{x} \\ \dot{y} \end{pmatrix}=\begin{pmatrix} 2 & 1 \\ 0 & 3 \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix}.$$
  3. $$\begin{pmatrix} \dot{x} \\ \dot{y} \end{pmatrix}=\begin{pmatrix} -1 & 1 \\ 0 & -2 \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix}.$$
Campo vectorial valores propios reales uno
Campo vectorial. Elaboración propia
Campo vectorial valores propios reales dos
Campo vectorial. Elaboración propia
Campo vectorial valores propios reales tres
Campo vectorial. Elaboración propia

Más adelante

En esta entrada logramos dibujar el plano fase para sistemas cuyos valores propios son reales distintos y no nulos. El siguiente paso será considerar aquellos sistemas que tienen valores propios complejos. Nuevamente dividiremos el análisis en tres casos, dependiendo del signo de la parte real de los valores propios. Eso lo haremos en la siguiente entrada.

¡No te la pierdas!

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Ecuaciones Diferenciales I – Videos: Puntos de equilibrio y estabilidad para sistemas de dos ecuaciones de primer orden

Por Eduardo Vera Rosales

Deja un comentario

Introducción

En la entrada anterior comenzamos el estudio a la teoría cualitativa de sistemas de dos ecuaciones de primer orden, definiendo el plano fase del sistema que es el plano $x(t)-y(t)$ junto con todas las curvas que representan a las soluciones al sistema de ecuaciones, vistas como funciones de $\mathbb{R}$ a $\mathbb{R}^{2}$. Una vez que escribimos al sistema de ecuaciones en la forma $$\dot{\textbf{X}}=\textbf{F}(x,y)$$ notamos que la función $\textbf{F}(x,y)$ puede ser vista como una función de $\mathbb{R}^{2}$ a $\mathbb{R}^{2}$. Más aún, podemos ver que a cada punto $(x,y)$ podemos anclar el vector $\textbf{F}(x,y)$ en el plano $x(t)-y(t)$. Este es el campo vectorial asociado al sistema, el cual nos da la información de cómo se ven las curvas solución y su comportamiento.

Para poder dibujar el plano fase de la forma más fiel posible aún debemos estudiar los puntos donde el campo $\textbf{F}$ se anula. A estos puntos los llamaremos puntos de equilibrio. De ellos dependerá casi por completo el comportamiento de las soluciones en el plano fase, por lo que estudiaremos su estabilidad. Es decir, veremos el comportamiento de las soluciones cercanas a los puntos de equilibrio conforme cambia la variable independiente $t$. Finalizaremos estudiando el plano fase de diversos sistemas e interpretando la estabilidad de los puntos de equilibrio según se recorren las curvas solución.

Puntos de equilibrio de sistemas de ecuaciones de primer orden

Definimos los puntos de equilibrio de un sistema de ecuaciones de primer orden y analizamos varios ejemplos. Además, probamos que $$\textbf{X}(t)=\begin{pmatrix} x_{0} \\ y_{0} \end{pmatrix}$$ es solución al sistema de ecuaciones lineal homogéneo con coeficientes constantes $$\dot{\textbf{X}}=\textbf{A}\textbf{X}$$ si $(x_{0},y_{0})$ es punto de equilibrio del sistema.

Estabilidad de puntos de equilibrio

Definimos los conceptos de puntos de equilibrio estables, asintóticamente estables e inestables. Mediante el plano fase estudiamos la estabilidad de puntos de equilibrio de diversos sistemas de ecuaciones.

Tarea moral

Los siguientes ejercicios no forman parte de la evaluación del curso, pero te servirán para entender mucho mejor los conceptos vistos en esta entrada, así como temas posteriores.

Los campos vectoriales de las imágenes fueron realizados en el siguiente enlace.

  • Considera el sistema lineal homogéneo con coeficientes constantes $\dot{\textbf{X}}=\textbf{A}\textbf{X}$. Muestra que si $\det{A} \neq 0$, entonces el único punto de equilibrio del sistema es $(0,0)$.
  • Considera nuevamente el sistema del ejercicio anterior $\dot{\textbf{X}}=\textbf{A}\textbf{X}$. Supongamos que $$\textbf{A}=\begin{pmatrix} a & b \\ c &d \end{pmatrix}$$ con $a\neq 0$ y $\det{A}=0$. ¿Qué puedes decir acerca de los puntos de equilibrio del sistema?
  • Encuentra un sistema de ecuaciones no lineales de primer orden sin puntos de equilibrio.
  • Calcula los puntos de equilibrio de los siguientes sistemas: $$\dot{\textbf{X}}=\begin{pmatrix} 1 & 4 \\ -2 & 7 \end{pmatrix}+\begin{pmatrix} 2 \\ 2 \end{pmatrix}.$$ $$\dot{\textbf{X}}=\begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix}+\begin{pmatrix} 0 \\ -\cos{x} \end{pmatrix}.$$ $$\dot{\textbf{X}}=\begin{pmatrix} 0 & 1 \\ 0 & -1 \end{pmatrix}+\begin{pmatrix} 0 \\ -\cos{x} \end{pmatrix}.$$
  • Determina la estabilidad de los puntos de equilibrio, según los campos vectoriales que aparecen a continuación:
estabildidad campo vectorial uno
Campo vectorial uno. Elaboración propia
estabilidad campo vectorial dos
Campo vectorial dos. Elaboración propia
estabiliddad campo vectorial tres
Campo vectorial tres. Elaboración propia

Más adelante

Una vez que conocemos los puntos de equilibrio de un sistema de ecuaciones de primer orden y definimos la estabilidad de estos, es momento para analizar el plano fase de los sistemas de dos ecuaciones con coeficientes constantes. Afortunadamente el plano fase y la estabilidad del (único) punto de equilibrio quedará determinado por la forma de los valores propios del sistema.

Comenzaremos en la siguiente entrada con el caso cuando el sistema tiene dos valores propios reales distintos y no nulos.

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Ecuaciones Diferenciales I – Videos: Geometría de soluciones a sistemas de dos ecuaciones de primer orden. Plano fase y campo vectorial asociado

Por Eduardo Vera Rosales

2 respuestas

Introducción

Bienvenidos a la última unidad del curso de Ecuaciones Diferenciales Ordinarias. En la unidad anterior estudiamos sistemas de ecuaciones diferenciales de primer orden de la forma $$\begin{alignedat}{4} \dot{x}_{1} &= F_{1}(t,x_{1},x_{2},…,x_{n}) \\ \dot{x}_{2} &= F_{2}(t,x_{1},x_{2},…,x_{n}) \\ & \; \; \vdots \notag \\ \dot{x}_{n} &= F_{n}(t,x_{1},x_{2},…,x_{n}) \end{alignedat}.$$ En particular, estudiamos a profundidad sistemas de ecuaciones lineales de primer orden con coeficientes constantes, los cuales se pueden escribir de forma abreviada como $$\dot{\textbf{X}}=\textbf{A}\textbf{X}$$ donde $\textbf{A}$ es una matriz cuadrada cuyas entradas son los coeficientes del sistema. Mediante el método de valores y vectores propios logramos hallar la solución general a tales sistemas dependiendo de la forma de la matriz $\textbf{A}$ y sus valores propios.

En esta unidad continuaremos estudiando sistemas de ecuaciones y sus soluciones pero desde un punto de vista cualitativo. En particular, nos enfocaremos en sistemas de dos ecuaciones de primer orden y en su plano fase, el cual es un dibujo que nos da la información suficiente para saber cómo se comportan las soluciones. Nos limitaremos inicialmente a estudiar ecuaciones lineales con coeficientes constantes, pero en próximas entradas analizaremos sistemas no lineales, los cuales no hemos resuelto de manera analítica (los métodos son complejos para abordar en un primer curso), pero podremos estudiarlos cualitativamente.

Comenzaremos en esta entrada definiendo el plano fase y el campo vectorial asociado al sistema, el cual nos ayudará a dibujar las curvas que representan a las soluciones del sistema, y veremos algunos ejemplos que nos ayudarán a entender tales conceptos.

¡Vamos a comenzar!

Plano fase de un sistema de dos ecuaciones de primer orden

Definimos el concepto de sistema de ecuaciones autónomo (cuyas ecuaciones no dependen explícitamente de la variable independiente $t$), asociamos a cada solución del sistema una curva en el plano $x(t) – y(t)$, y definimos el plano fase asociado al sistema.

Campo vectorial asociado al sistema

Definimos el campo vectorial asociado a un sistema de dos ecuaciones y estudiamos la relación que guarda con las curvas del plano fase del sistema.

Tarea moral

Los siguientes ejercicios no forman parte de la evaluación del curso, pero te servirán para entender mucho mejor los conceptos vistos en esta entrada, así como temas posteriores.

Los campos vectoriales de las imágenes fueron realizados en el siguiente enlace.

  • Encuentra la solución general al sistema $$\dot{\textbf{X}}=\begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix}\textbf{X}.$$ ¿Cuál es el campo vectorial asociado al sistema? Dibuja a mano algunos vectores del campo vectorial, y algunas curvas solución en el plano fase. ¿Puedes dibujarlas todas con la información obtenida?
  • Encuentra la solución general al sistema $$\dot{\textbf{X}}=\begin{pmatrix} 1 & 2 \\ 0 & -1 \end{pmatrix}\textbf{X}.$$ Dibuja algunas curvas solución en el plano fase. En la siguiente imagen puedes ver el campo vectorial asociado.
Campo vectorial asociado al problema
Campo vectorial asociado al sistema del problema. Elaboración propia
  • Resuelve el sistema $$\dot{\textbf{X}}=\begin{pmatrix} 1 & 0 \\ 0 & 0 \end{pmatrix}\textbf{X}+\begin{pmatrix} 0 \\ 1\end{pmatrix}.$$ Dibuja algunas curvas solución en el plano fase. En la siguiente imagen puedes ver el campo vectorial asociado.
Campo vectorial asociado al problema
Campo vectorial asociado al sistema del problema. Elaboración propia
  • En el primer video vimos que cada solución a un sistema $\dot{\textbf{X}}=\textbf{A}\textbf{X}$ determina una curva en el plano fase. Considera ahora una curva solución en el plano fase. ¿Determina una única solución al sistema? Es decir, ¿esta curva representa a una única solución al sistema?
  • Considera el sistema $$\dot{\textbf{X}}=\begin{pmatrix} 1 & 2 \\ -2 & 1 \end{pmatrix}\textbf{X}.$$ Determina si el siguiente dibujo puede representar al campo vectorial asociado.
Campo vectorial. Elaboración propia

Más adelante

Una vez que hemos definido el plano fase de un sistema de dos ecuaciones $\dot{\textbf{X}}=\textbf{F}(x,y)$, vamos a comenzar a estudiar el comportamiento de las curvas solución. Para esto debemos estudiar los puntos de equilibrio, que serán aquellos puntos $(x,y)$ tales que $\textbf{F}(x,y)=(0,0)$. De dichos puntos va a depender el comportamiento del plano fase entero, por lo que estudiaremos su estabilidad.

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Ecuaciones Diferenciales I – Videos: Teorema de existencia y unicidad para sistemas de ecuaciones de primer orden

Por Eduardo Vera Rosales

Deja un comentario

Introducción

Vamos a concluir la tercera unidad del curso revisando el teorema de existencia y unicidad para sistemas de ecuaciones de primer orden, en su forma general, es decir, para sistemas lineales y no lineales que satisfagan las hipótesis del teorema. Hasta el momento únicamente demostramos el teorema de existencia y unicidad para sistemas lineales con coeficientes constantes, pero es importante demostrar la versión general al igual que hicimos para las ecuaciones de primer orden.

Lo primero que veremos es que un sistema de ecuaciones de la forma $$\begin{alignedat}{4} \dot{x}_{1} &= F_{1}(t,x_{1},x_{2},…,x_{n}) \\ \dot{x}_{2} &= F_{2}(t,x_{1},x_{2},…,x_{n}) \\ & \; \; \vdots \notag \\ \dot{x}_{n} &= F_{n}(t,x_{1},x_{2},…,x_{n}) \end{alignedat}$$ se puede escribir en forma abreviada como sigue: $$\dot{\textbf{X}}(t)=\textbf{F}(t,\textbf{X}(t))$$ donde $\textbf{F}$ es el vector conformado por las funciones $F_{i}$ del sistema, con $i \in \{1,…,n\}$. Si además agregamos la condición inicial $\textbf{X}(t_{0})=\textbf{Y}$, entonces podemos ver que el sistema se reduce a una expresión muy similar al problema de condición inicial $$\frac{dy}{dt}=f(t,y(t)) \,\,\,\,\, ; \,\,\,\,\, y(t_{0})=y_{0}$$ salvo que ahora $\textbf{X}$ es una función que toma valores en $\mathbb{R}^{n}$, y $\textbf{F}$ es una función de $\mathbb{R}^{n+1}$ a $\mathbb{R}^{n}$.

Afortunadamente la mayoría de los lemas y teoremas que usamos para demostrar el teorema de existencia y unicidad para ecuaciones de primer orden se pueden extender a funciones de varias variables, por lo que la demostración será muy similar a la demostración de este último teorema.

Antes de iniciar te dejo la entrada correspondiente al teorema de existencia y unicidad de Picard, para que te familiarices con él y te sea más fácil ver los videos de esta entrada.

El teorema de existencia y unicidad para sistemas de ecuaciones de primer orden. Ecuación integral asociada

Enunciamos el teorema de existencia y unicidad para sistemas de ecuaciones de primer orden, analizamos las similitudes que existen con el teorema de existencia y unicidad de Picard, y vemos que resolver el problema de condición inicial es equivalente a resolver la ecuación integral $$\textbf{X}(t)=\textbf{Y}+\int_{t_{0}}^{t} \textbf{F}(s, \textbf{X}(s)) \, ds.$$

Demostración de la existencia de la solución al problema de condición inicial

Demostramos la existencia de una solución al problema de condición inicial estudiando bajo qué circunstancias converge uniformemente la sucesión de iteraciones de Picard del problema. En dado caso que esto último suceda, la función a la cual convergen las iteraciones será solución a la ecuación integral del video anterior.

Demostración de la unicidad de la solución al problema de condición inicial

Concluimos la demostración del teorema probando la unicidad de la solución al problema de condición inicial.

Tarea moral

Los siguientes ejercicios no forman parte de la evaluación del curso, pero te servirán para entender mucho mejor los conceptos vistos en esta entrada, así como temas posteriores.

  • Sea $\textbf{F}(t,\textbf{X}(t))$ continua en un dominio $E \subseteq \mathbb{R}^{n+1}$ que contenga a $(t_{0},\textbf{Y})$. Demuestra que $\textbf{X}(t)$ es solución al problema de condición inicial $$\dot{\textbf{X}}(t)=\textbf{F}(t,\textbf{X}(t)) \,\,\,\,\, ; \,\,\,\,\, \textbf{X}(t_{0})=\textbf{Y}$$ si y sólo si es solución a la ecuación integral $$\textbf{X}(t)=\textbf{Y}+\int_{t_{0}}^{t} \textbf{F}(s,\textbf{X}(s)) \, ds.$$
  • Considera el problema de condición inicial $$\dot{\textbf{X}}=\begin{pmatrix} 0 & 1\\ 1 & 0 \end{pmatrix} \textbf{X} + \begin{pmatrix} t \\ t \end{pmatrix} \,\,\,\,\, ; \,\,\,\,\, \textbf{X}(0)=\begin{pmatrix} 1 \\ -1 \end{pmatrix}.$$ Calcula las iteraciones de Picard correspondientes al problema. ¿Convergen a alguna función? En caso afirmativo, muestra que dicha función es solución al problema de condición inicial.
  • Supongamos que $\textbf{F}(t,\textbf{X}(t))$ es continua en $$R:=\{(t,x_{1},…,x_{n}) \in \mathbb{R}^{n+1} : |t-t_{0}| \leq a, \lVert \textbf{X}(t) – \textbf{Y} \rVert \leq b, \, \, a, b \in \mathbb{R}\}.$$ Demuestra que existe $M > 0$ y $h \in \mathbb{R}$ tal que $$\lVert \textbf{X}^{n}(t)-Y \rVert \leq M |t-t_{0}|, \forall n \in\mathbb{N}, \forall t \in I_{h} \subseteq \mathbb{R}.$$ Recuerda que $\textbf{X}^{n}(t)$ es la $n$-ésima iteración de Picard correspondientes al problema de condición inicial que estudiamos a lo largo de la entrada. (Hint: La prueba es similar al lema análogo que probamos en este video para el teorema de existencia y unicidad de Picard).
  • Consideremos el problema de condición inicial $$a\frac{d^{2}y}{dt^{2}}+b\frac{dy}{dt}+cy=0 \,\,\,\,\, ; \,\,\,\,\, y(t_{0})=y_{0} \,\,\,\,\, ; \,\,\,\,\, \frac{dy}{dt}(t_{0})=y_{1}$$ con $a,b,c$ constantes. ¿Si el sistema de ecuaciones asociado satisface el teorema de existencia y unicidad, entonces el problema de condición inicial original tiene una única solución?

Más adelante

Con este teorema finalizamos la tercera unidad del curso. En la cuarta unidad comenzaremos con la teoría cualitativa de los sistemas de ecuaciones de primer orden.

Veremos que los sistemas tienen puntos de equilibrio, los clasificaremos según su estabilidad. En virtud de esto vamos a analizar el comportamiento de las soluciones cerca de puntos de equilibrio y dibujaremos el plano fase de un sistema.

Abordaremos sistemas no lineales, y aunque no los resolveremos explícitamente, veremos el comportamiento de sus soluciones cerca de sus puntos de equilibrio.

Finalmente, veremos algunos sistemas que satisfacen propiedades interesantes, como los sistemas Hamiltonianos, los disipativos, entre otros.

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»