Introducción

Un problema clásico de la geometría es el Problema de Apolonio el cual enuncia:

Encontrar una circunferencia dado tres condiciones, las cuales pueden surgir de lo siguiente:

1. La circunferencia pasa por uno o más puntos «P»
2. La circunferencia es tangente a una o más líneas «L»
3. La circunferencia debe de ser tangente a uno o más círculos «C»

De lo anterior nacen los 10 Problemas de Apolonio (Las soluciones se darán a partir de construcciones).

Los Diez Problemas de Apolonio

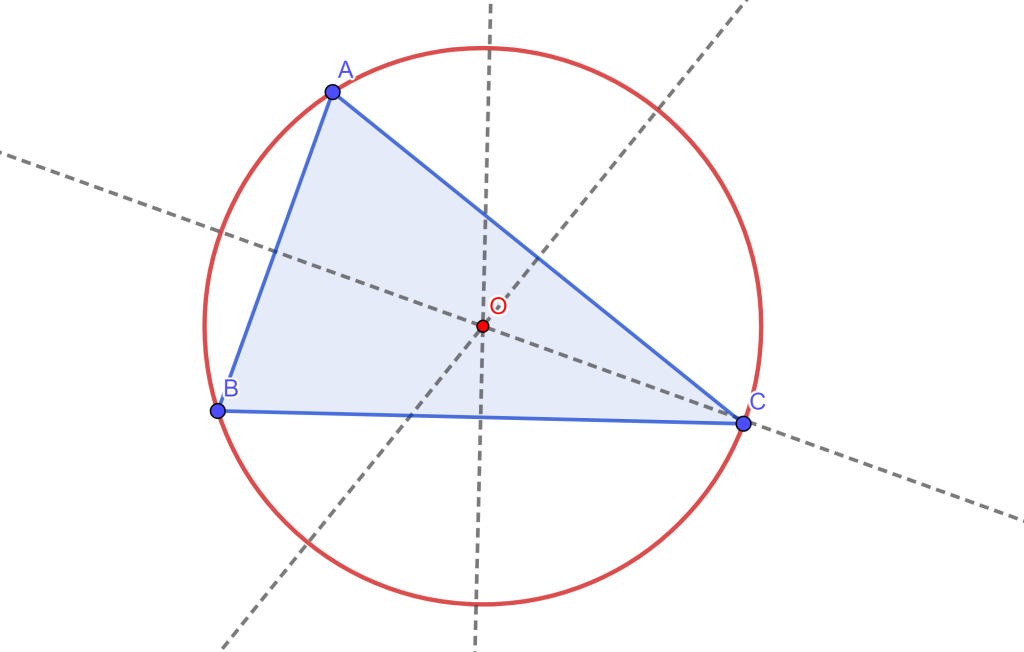
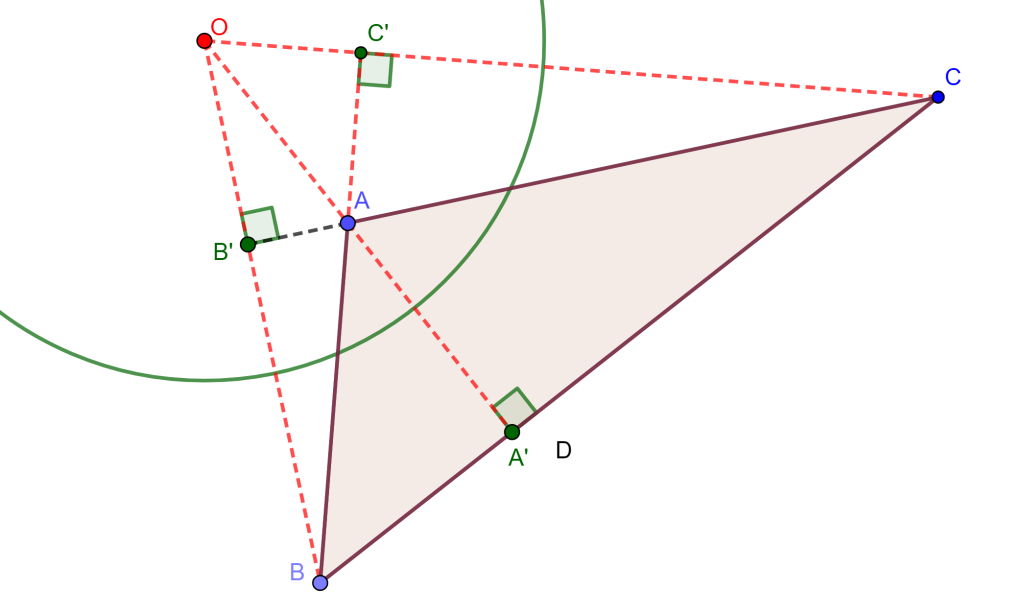
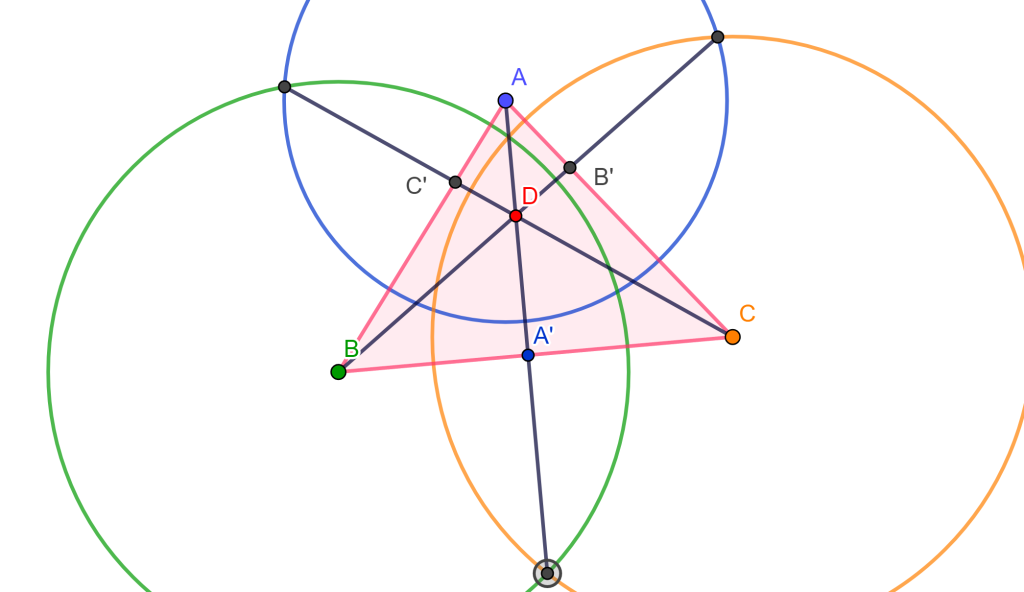
Problema 1. Construir una circunferencia que pase por tres puntos dados (PPP).

Construcción. Dados tres puntos $A$, $B$ y $C$, de los cuales podemos formar un triángulo $\triangle ABC$. Trazando las mediatrices de cada lado encontraremos el circuncentro «$O$», que resulta ser el centro de la circunferencia circunscrita al triángulo $\triangle ABC$. De esta forma podemos dibujar la circunferencia $C(O,r)$.

$\square$

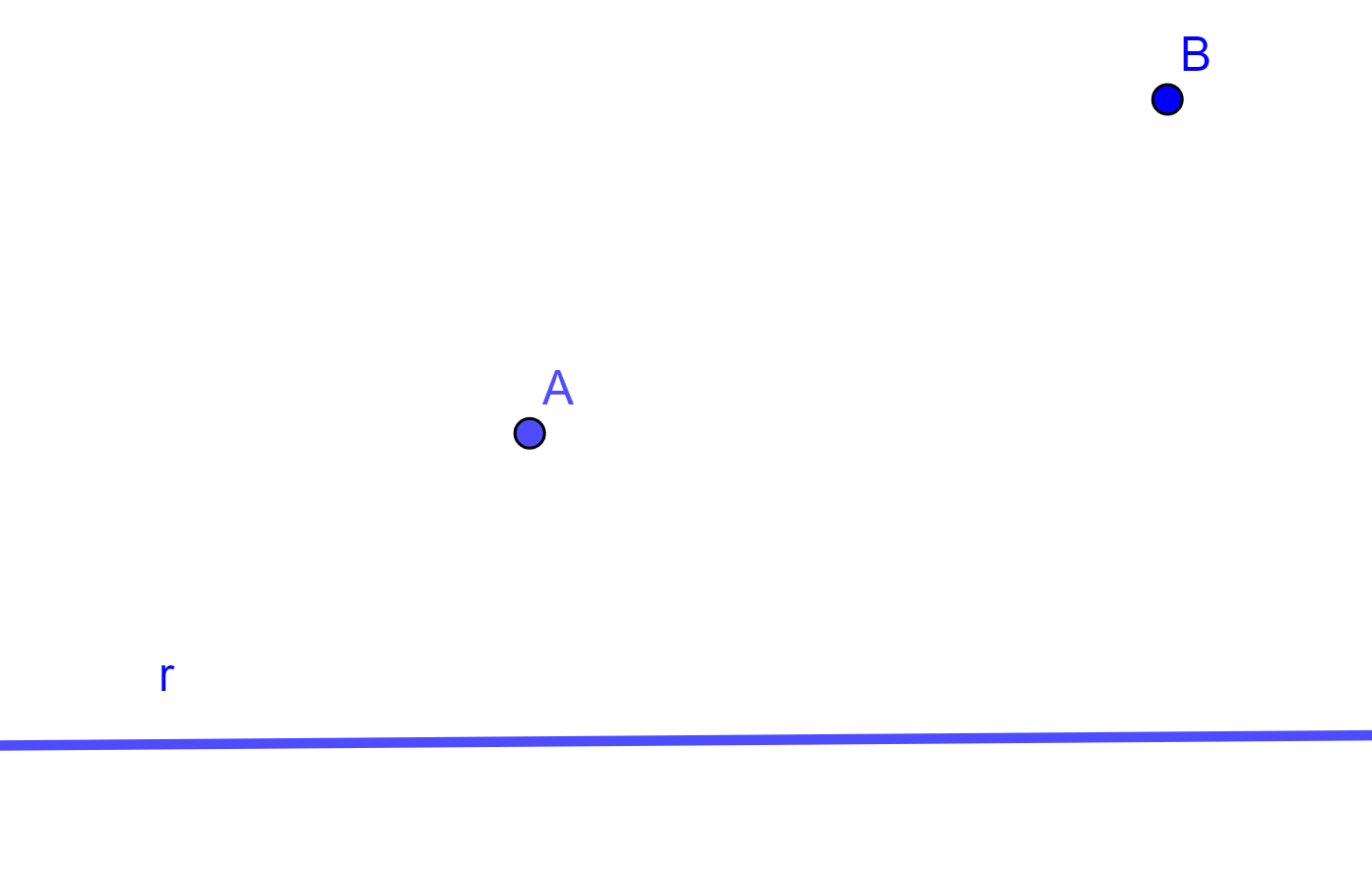
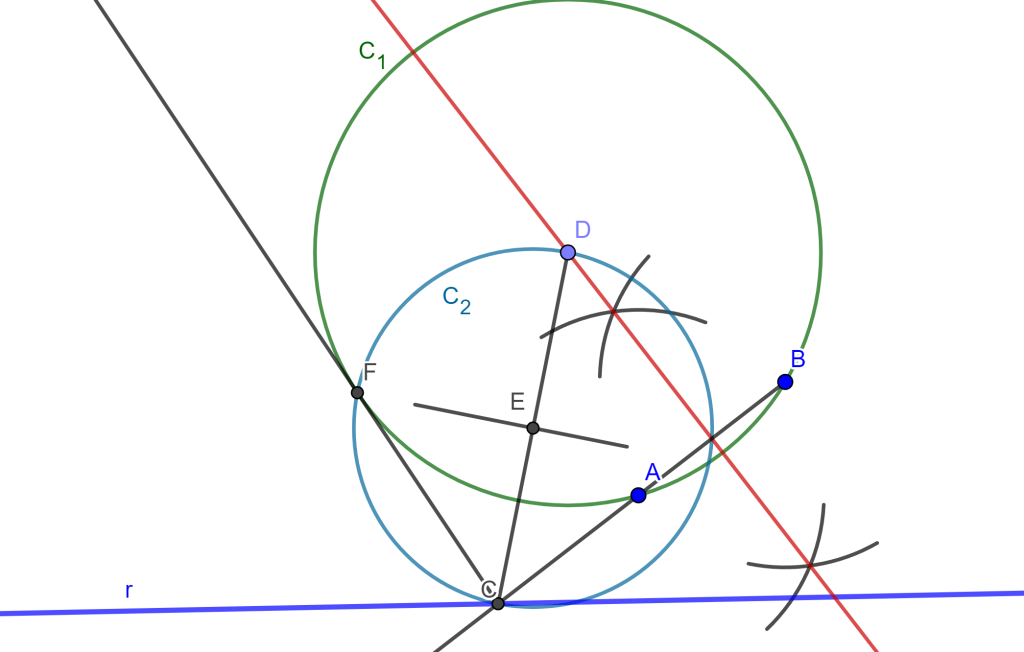
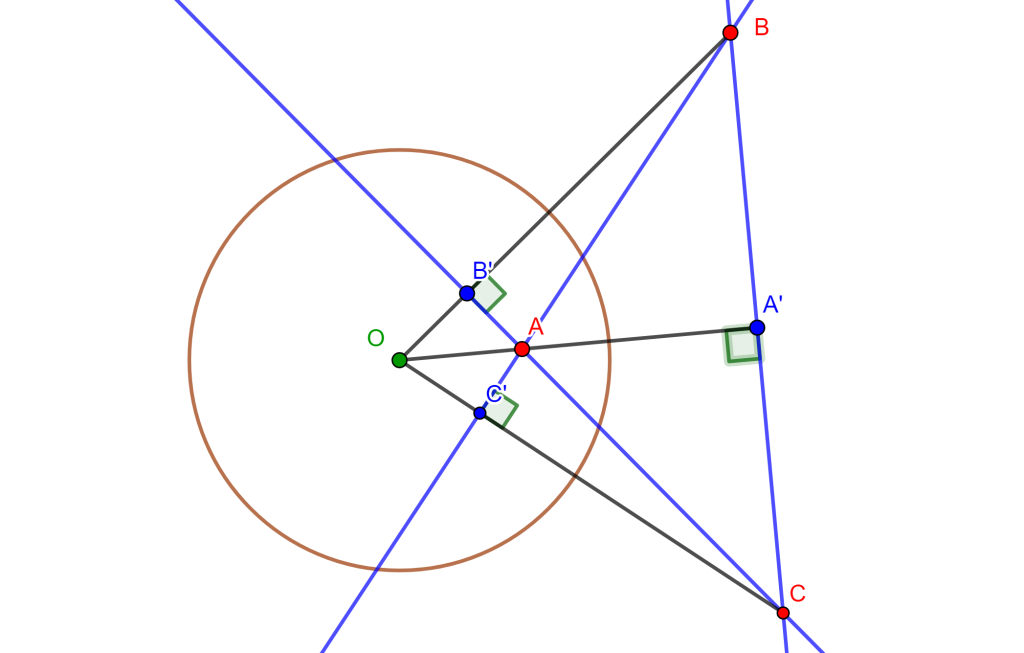
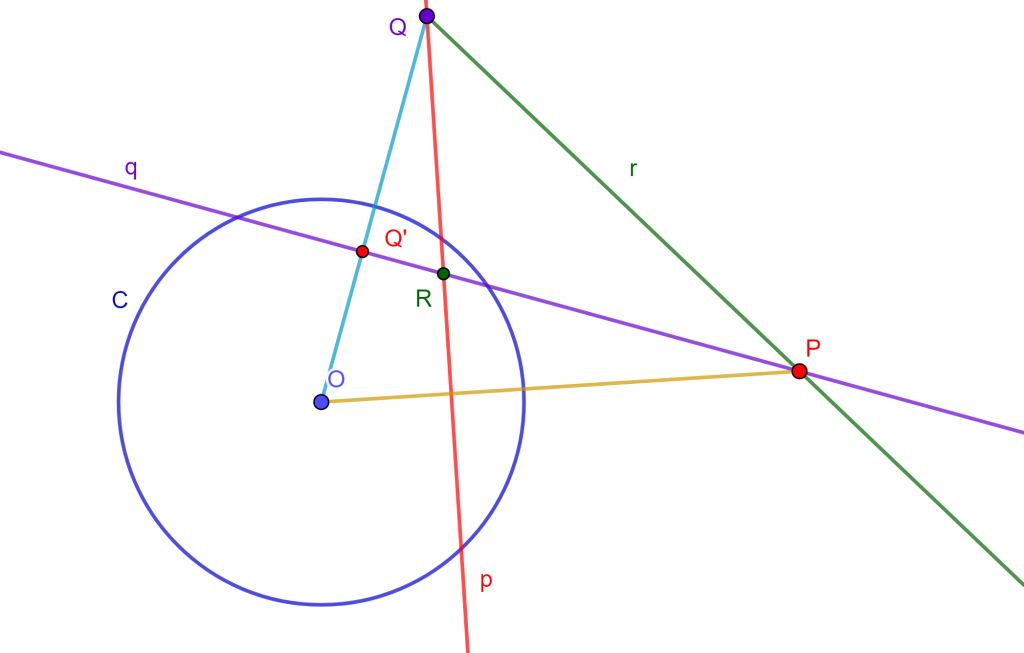
Problema 2. Construir una circunferencia que pase por dos puntos dados y tangente a una recta dada (PPL).

Construcción. Sean $A$ y $B$ dos puntos dados y $r$ una recta tangente a la circunferencia buscada.

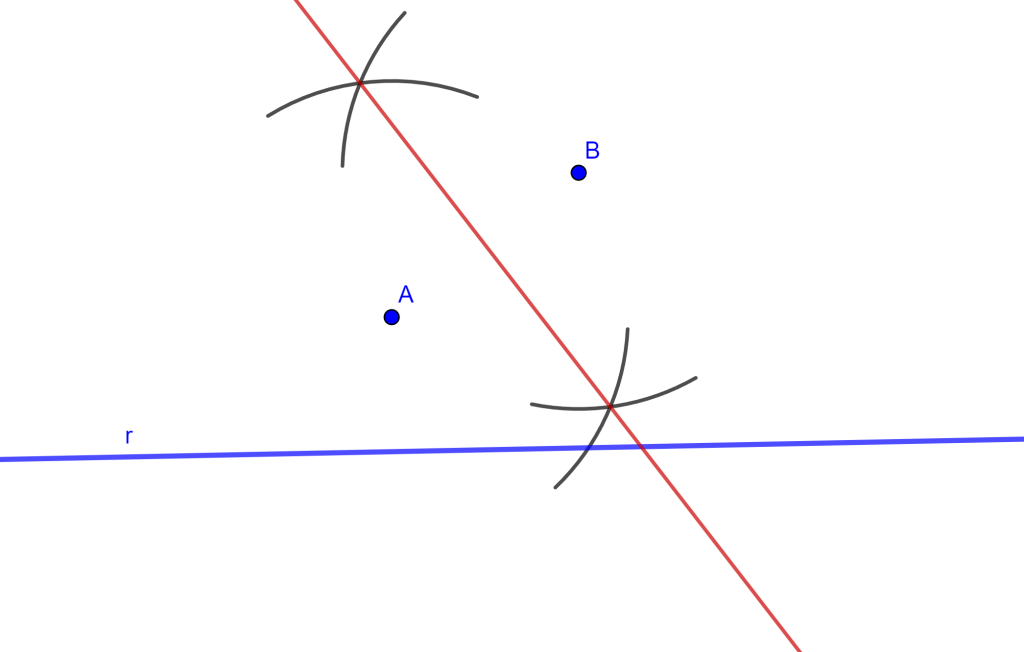
El centro de la circunferencia buscada $C$ debe estar ubicada en la mediatriz del segmento $AB$, por ello dibujemos la mediatriz a través del arco de dos circunferencias con centro $A$ y centro $B$ las cuales se intersecan y se puede trazar la mediatriz.

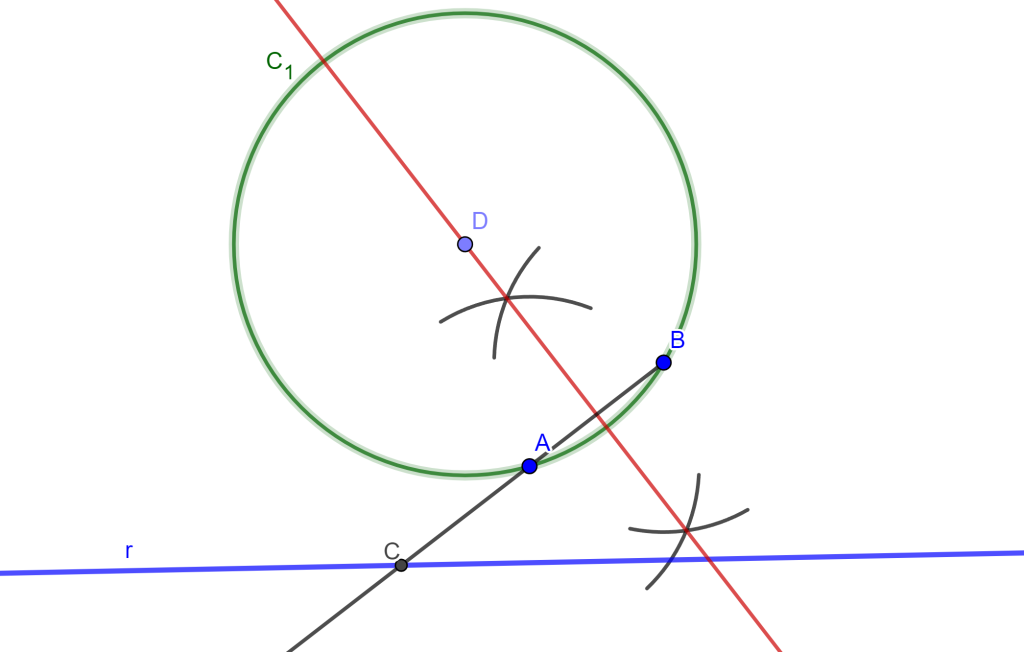
Ahora tomamos un punto «$D$» de la mediatriz, del cual lo tomamos como centro de una circunferencia $C_1$ que pase por $A$ y $B$. También trazamos el segmento $AB$ que corte $r$ en $C$.

Debemos de encontrar una recta tangente a $C_1$ y que pase por el punto $C$. Por ello unimos $DC$ y sacamos la mediatriz con centro $E$, trazamos la circunferencia $C_2$ que interseca a $C_1$ en dos puntos del cual solo nos interesa uno que es $F$ y al unirlo con $C$ este forma una recta tangente a $C_1$.
Por ahora tenemos por potencia $CA * CB = CF^2$.

Ahora trazamos el arco de circunferencia con centro $C$ y radio $CF$ que corta a la recta $r$ en dos puntos $T_1$ y $T_2$ cumplen $CA * CB =CF^2 =CT_1^2 = CT_2^2$ perpendiculares por $T_1$ y otra por $T_2$, y cortan a la mediatriz $AB$.
Y en esas intersecciones van a estar los centros de las circunferencias que pasan por $A$, $B$ y tangentes a $r$.

$\square$

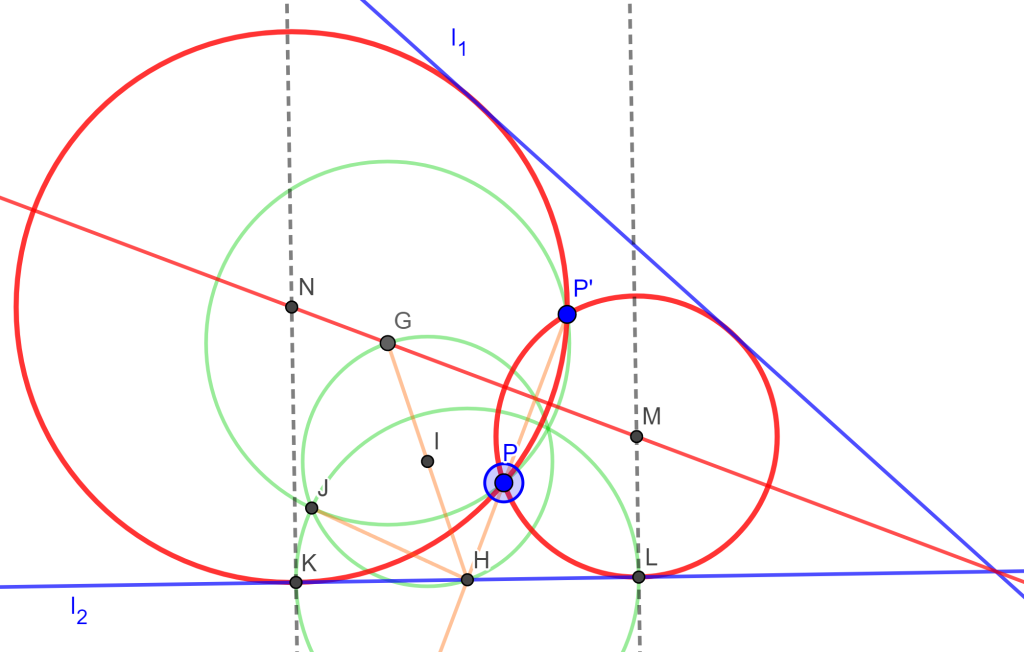
Problema 3. Construir una circunferencia tangente a dos líneas dadas y que pasa por un punto (PLL).

Construcción. Sean $l_1$ y $l_2$ dos rectas dadas y $P$ un punto dado, notemos que el centro de la circunferencia buscada es un punto de la bisectriz; Por otro lado, la circunferencia buscada debe contener a $P$ y $P’$ punto simétrico respecto a la bisectriz.
Si observamos tenemos el caso del problema 2 PPL, ya que tenemos dos puntos $P$ y $P’$ por los cuales pasara la circunferencia buscada, además de que es tangente a una recta $l_1$. Por tal motivo se puede seguir la misma construcción anterior para llegar a la solución.

$\square$

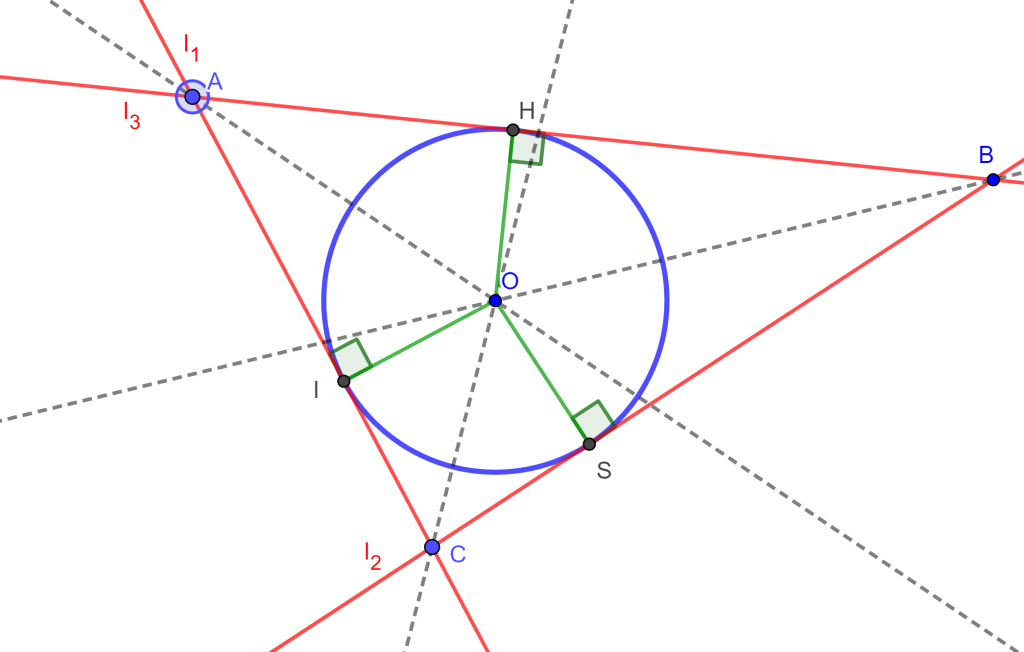
Problema 4. Construir un círculo tangente a tres líneas dadas (LLL).

Construcción. Sean tres rectas dadas $l_1$, $l_2$ y $l_3$, las cuales forman un triángulo $\triangle ABC$. Trazando las bisectrices de los ángulos internos del triángulo $\triangle ABC$ se intersecan en un único punto $O$.
El punto $O$ es el centro de la circunferencia inscrita del triángulo $\triangle ABC$ , ahora trazamos las perpendiculares por $O$ a cada lado y encontraremos el radio $OS$ el cual nos da la circunferencia tangente a $l_1$, $l_2$ y $l_3$.

$\square$

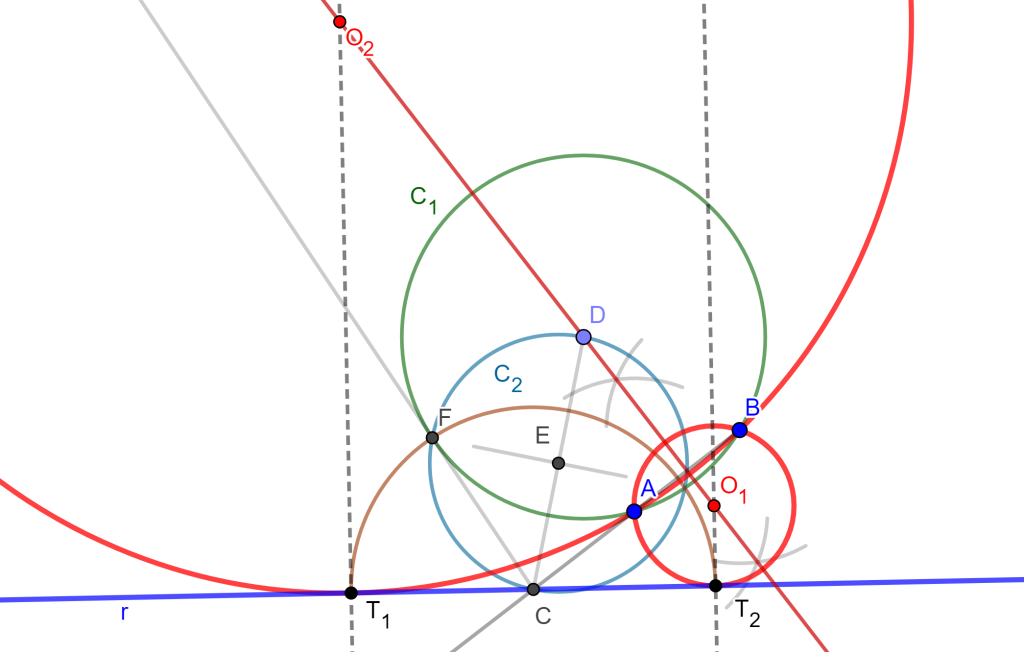
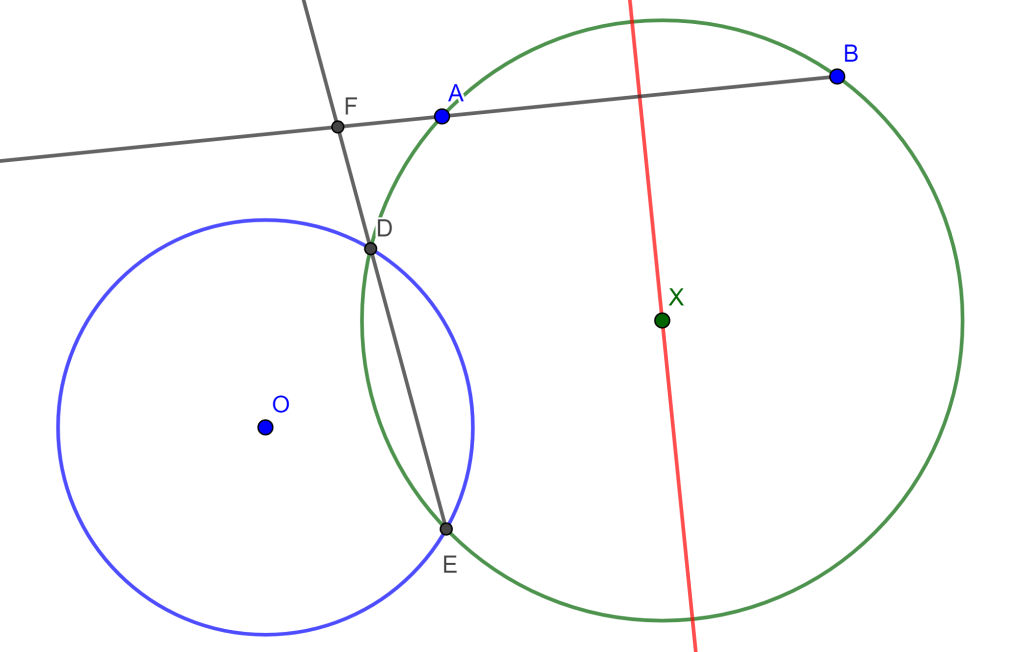
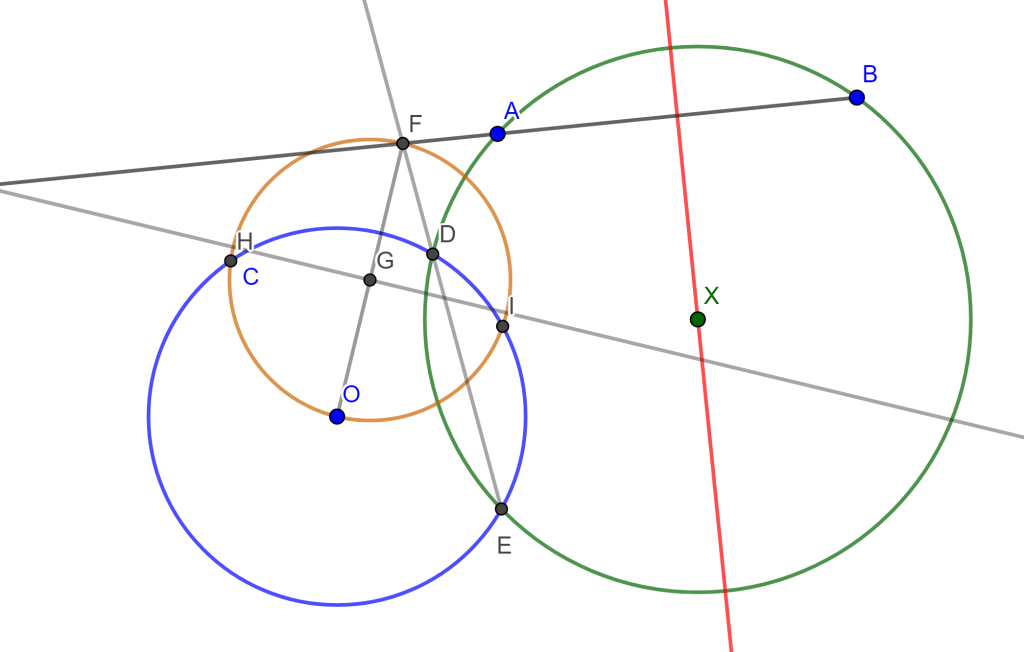
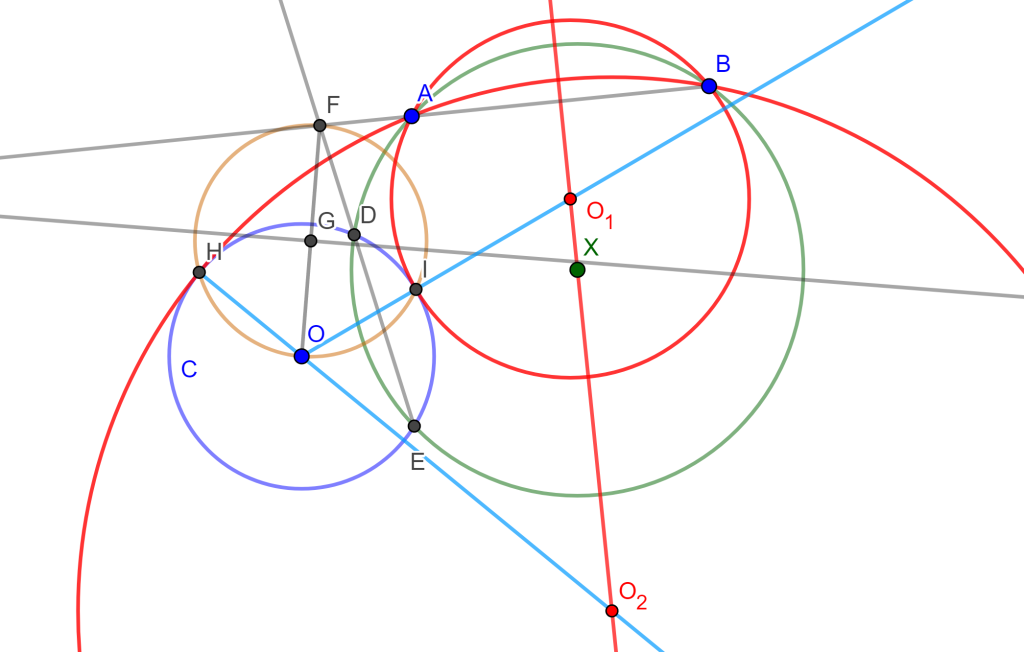
Problema 5. Construye una circunferencia pasando por dos puntos dados y tangente a un círculo dado (PPC).

Construcción. Existen varios casos para este problema, en este caso tomaremos a los puntos $A$ y $B$ fuera de la circunferencia dada $C(O,r)$.
Trazamos la mediatriz de $A$ y $B$, después tomamos un punto cuál sea $x$ en la mediatriz y generamos una circunferencia con centro en $x$ y radio $A$ o $B$ y que corta a la circunferencia $C(O,r)$. Los dos puntos de intersección los llamaremos $D$ y $E$ los uniremos y prolongaremos hasta que corte a la recta $AB$, el punto de intersección será $F$.

Unimos $F$ con $O$ y sacamos su mediatriz, denotamos a $G$ al punto de intersección de $FO$ con la mediatriz. Ahora trazamos la circunferencia con centro $G$ y radio $O$ la cual corta a $C(O,r)$ en $H$ y $I$.

Si unimos $I$ con $O$ corta a la mediatriz $AB$ en $O_1$, el cual será el centro de la circunferencia buscada con radio $O_1I$ y por lo cual pasa por $A$, $B$ y tangente $C(O,r)$. Ocurre lo mismo si unimos $H$ con $O$, corta a la mediatriz de $AB$ en $O_2$, este sería el centro $O_2$ y radio $O_2A$, el cual genera la otra circunferencia tangente a $C(O,r)$ y pasa por $A$ y $B$.

$\square$

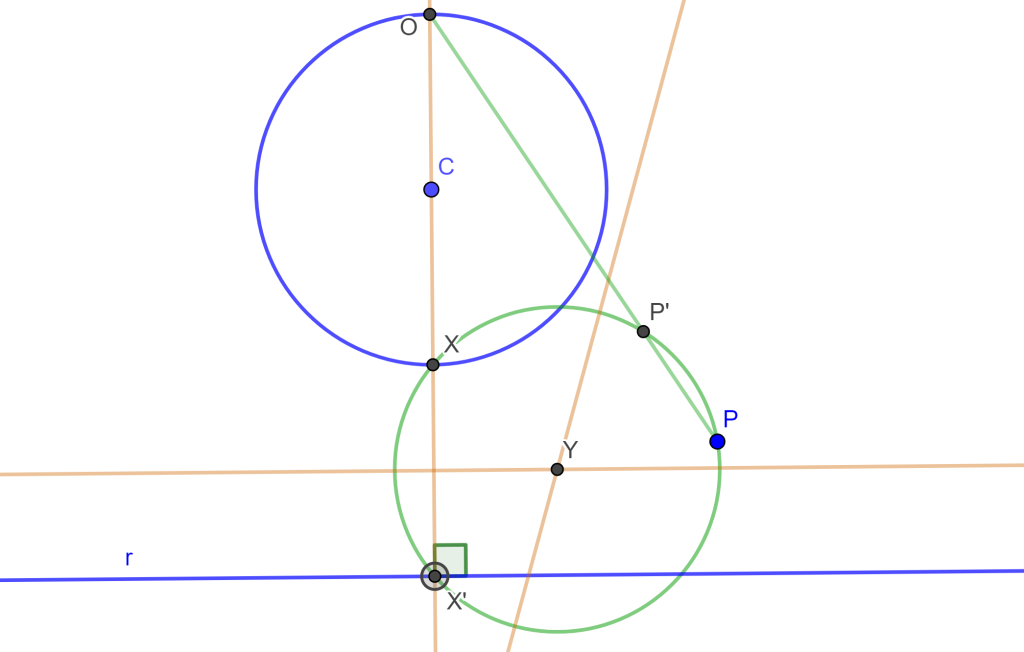
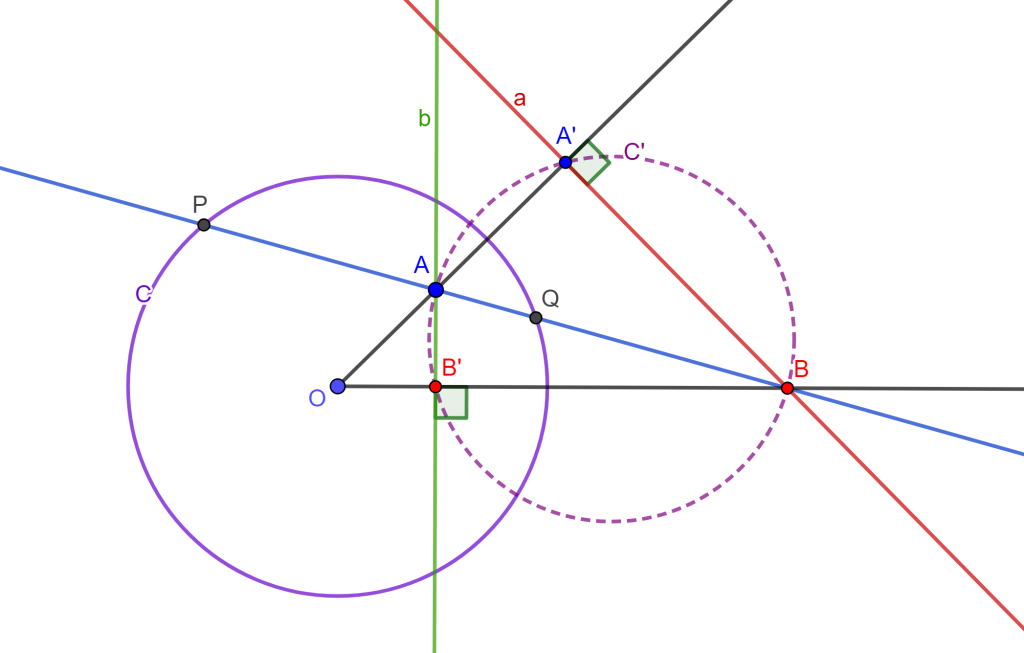
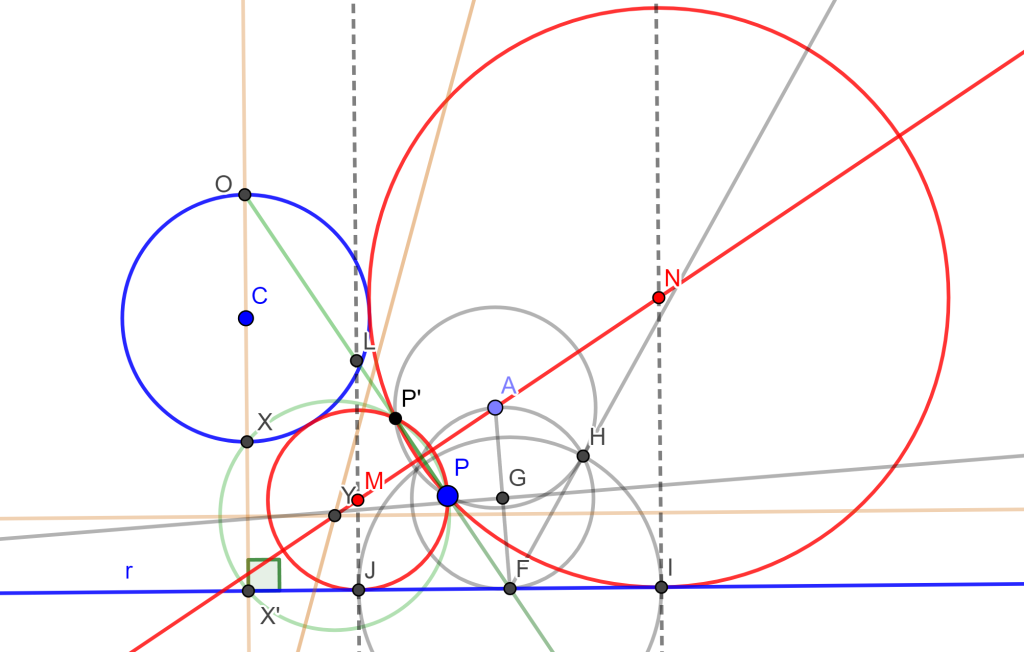
Problema 6. Construir una circunferencia que pase por un punto dado, tangente a una recta dada y tangente a un círculo dado (PLC).

Construcción. Para este problema 6 podemos encontrar cuatro soluciones, pero por ahora solo se dará una parte de la construcción, ya que lo demás ya se ha venido trabajando en las construcciones anteriores.
Tenemos la circunferencia $C$, el punto $P$ y la recta $r$. Trazamos una perpendicular a $r$ que pase por $C$, ahora sea $O$ el punto de corte que será el centro de inversión que convierte la circunferencia $C$ en la recta $r$, entonces los puntos $x$ y $x’$ son inversos.
Ahora debemos encontrar el punto inverso de $P$, por ello trazamos la mediatriz de $xx’$ y trazamos la mediatriz de $xP$, estas dos rectas cortan en $Y$ el cual es el centro de circunferencia que corto a $x$, $x’$ y $P$, y el punto de intersección de esta circunferencia con la recta $OP$ tendremos $P’$.

Nos daremos cuenta de que tenemos el mismo problema 2 PPL, por lo cual solo se debe seguir la misma construcción para hallar las circunferencias buscadas.

De aquí en adelante se enunciarán únicamente los problemas faltantes.

Problema 7. Construir una circunferencia que pase por un punto $P$ dado y dos círculos tangentes a esta circunferencia buscada (PCC) (4 soluciones).

Problema 8. Construir una circunferencia tangente a dos rectas dadas y a un círculo dado (LLC) (8 soluciones).

Problema 9. Construir una circunferencia tangente a una línea dada y a dos círculos dados (LCC) (8 soluciones).

Problema 10. (Problema de Apollonius) Construir una circunferencia tangente a tres círculos dados (CCC).

Más adelante…

Una vez visto el tema de Polos y Polares, es hora de realizar unos ejercicios que se dejaran, todo con el objetivo de fortalecer los temas vistos.

Entradas relacionadas

• Ir a Geometría Moderna II
• Entrada anterior del curso: Circunferencia Polar
• Siguiente entrada del curso: Ejercicios Unidad 3

Introducción

Como ya se vio en la entrada anterior de Triángulo Autopolar, se puede tener un triángulo autopolar dada una circunferencia y no solo eso, sino que además se puede tener un número infinito de triángulos autopolares dada una circunferencia, pero solamente existe una circunferencia (Circunferencia Polar) de la cual un triángulo dado sea autopolar.

Circunferencia Polar

Como mencione, solo existe una circunferencia de la cual un triángulo dado sea autopolar, donde el triángulo debe de ser obtuso. Por lo cual si se cumple lo anterior se tiene una circunferencia que se denomina Circunferencia Polar del triángulo.

Construcción. Dado $A$ un punto dado y $BC$ una recta dada. Supongamos $O$ el centro de la circunferencia, dado que la polar de $B$ pasa por $A$ y perpendicular a $BO$, y la polar de $C$ pasa por $A$ y perpendicular a $CO$, entonces $O$ es el ortocentro del triángulo $\triangle ABC$.

Ahora como el polo $A$ es el vértice, y el pie de la altura $D$ el cual pertenece a la polar de $A$ son puntos inversos, entonces $r= \sqrt{AO \times DO} $, de esta forma encontramos la circunferencia polar del triángulo $\triangle ABC $ la cual es única.

El triángulo $\triangle ABC $ es autopolar.

$\square$

Propiedad. Cualquier circunferencia la cual tiene una cuerda como altura del triángulo es ortogonal a la circunferencia polar del triángulo.

De la construcción anterior se tiene:

Propiedad. Si un triángulo es autopolar con respecto a una circunferencia, entonces el triángulo es obtusángulo.

Demostración. Se sabe que el $\triangle ABC$ es autopolar con respecto a la circunferencia $C(O,r)$ y se tiene que $O$ es el ortocentro. Además, $OA \times OA’ = OC \times OC’ = OB \times OB’ =r^2$.

Ahora supongamos $O$ interno al triángulo $\triangle ABC$, entonces los puntos inversos de cada par estarían en lados contrarios de sus respectivas líneas respecto a $O$ centro de inversión, entonces $OA \times OA’ = OC \times OC’ = OB \times OB’ =-r^2$. Por lo cual $O$ debe de ser un punto externo al triángulo $\triangle ABC$.

Entonces $\angle BAC$ es un angulo externo a $\triangle B’BA$, entonces $\angle BAC= \angle BB’A + \angle ABB’ = \pi /2 + \angle ABB’$, se tiene que $\angle BAC > \pi /2$. Por lo tanto, el $\triangle ABC$ es obtusangulo.

$\square$

Teorema. El circuncirculo de un triángulo autopolar y su circunferencia de los nueve puntos son mutuamente inversas con respecto a la circunferencia polar.

Propiedad. Tres de los cuatro triángulos de un grupo ortocentrico son obtusos.

Los triángulos $DAB$, $DBC$ y $ DCA$ son obtusos en $D$, se tienen $r_C$, $r_A$ y $r_B$ los radios de las circunferencias polares $C$, $A$ y $B$ de estos triángulos respectivamente.

Entonces se tiene $r^2_B=BA’ \times BC$ y $r^2_C=A’C \times BC$, de lo anterior se obtiene $r^2_B + r^2_C = (BA’ \times A’C) BC = BC^2$.

De esta forma las circunferencias $B$ y $C$ son ortogonales, como $A’$ y $C$ son puntos inversos con respecto a la circunferencia $B$, $A’A$ es la polar de $C$ respecto a la circunferencia $B$ y pasa por los puntos de intersección de las circunferencias $B$ y $C$, por lo cual se tiene el siguiente teorema.

Teorema. Dados los tres triángulos obtusos de un grupo ortocentrico sus circunferencias polares son ortogonales en pares, y sus puntos de intersección están en los tres lados de un cuadrángulo que pasa por el vértice común de los ángulos obtusos.

Más adelante…

Se abordarán los 10 problemas de Apolonio.

Entradas relacionadas

• Ir a Geometría Moderna II
• Entrada anterior del curso: Principio de dualidad y Triángulo Autopolar
• Siguiente entrada del curso: Los diez problemas de Apolonio

Introducción

Gracias a la relación de polos y polares con respecto a una circunferencia, se tenían correspondencias entre todos los puntos y todas las rectas del plano. Por lo cual nace el Principio de dualidad. Así mismo analizaremos el Triángulo Autopolar junto con algunas propiedades.

Principio de Dualidad

El principio de Dualidad, donde la propiedad que nos dé como resultado de intercambiar las palabras de recta y punto resulta verdadera, además de que guarda sus propiedades.

Por ejemplo, se tiene la siguiente dualidad del teorema con respecto a su corolario.

Teorema. Dada una circunferencia, la polar de $P$ pasa por $Q$, entonces la polar de $Q$ pasa por $P$.

Corolario. Dada una circunferencia, sean $p$ y $q$ rectas tales que, el polo de $p$ está en $q$, entonces el polo de $q$ está en $p$.

Se puede ver que ambos son duales, se puede dar un ejemplo más sencillo.

Ejemplo. La unión de dos puntos es una recta, entonces la intersección de dos rectas es un punto.

Triángulo Autopolar

Definición. Se define como triángulo autopolar a aquel que, con respecto a una circunferencia, se tiene que cada vértice es el polo del lado opuesto, de tal modo que cada lado es polar del vértice opuesto.

Construcción. Se tiene una circunferencia $C(O,r)$, tomemos un punto $A$ dentro de la circunferencia y tracemos su inverso $A’$ y $a$ su polar. Ahora tomemos un punto $B$ en $a$ tal que $A’ \neq B$ y trazamos $b$ su polar, y por el Teorema Fundamental de Polos y Polares se tiene que $b$ pasa por $A$. Además, a la intersección de $a$ y $b$ la llamaremos $C$, y su polar de $c$ pasa por $A$ y $B$ puntos.

De esta forma tenemos el $ \triangle ABC$ es autopolar con respecto a $C(O,r)$.

$\square$

Propiedades

Se tienen varias propiedades del triángulo autopolar.

1.- El ortocentro del triángulo autopolar es el centro de la circunferencia.

Demostración. De la figura anterior se tiene que:

La polar de $A$ es $a$ que es el lado $BC$ del $ \triangle ABC$ y $BC \perp OA$ por $A’$ inverso de $A$.

La polar de $B$ es $b$ que es el lado $CA$ del $ \triangle ABC$ y $CA \perp OB$ por $B’$ inverso de $B$.

La polar de $C$ es $c$ que es el lado $AB$ del $ \triangle ABC$ y $AB \perp OC$ por $C’$ inverso de $C$.

Por lo cual $AA’$, $CC’$ y $BB’$ son las alturas del $ \triangle ABC$ y estas se intersecan en $O$.

Por lo tanto, $O$ es el ortocentro del $\triangle ABC$.

$\square$

2.- Uno de sus vértices está dentro de la circunferencia y los otros dos fuera de esta.

3.- El ángulo del triángulo cuyo vértice está en la circunferencia es obtuso.

Más adelante…

Se abordará el tema de circunferencia Polar, en el cual veremos su relación con polos y polares.

Entradas relacionadas

• Ir a Geometría Moderna II
• Entrada anterior del curso: Relaciones Armónicas
• Siguiente entrada del curso: Circunferencia Polar