Introducción

En esta nueva entrada hablaremos acerca de una nueva operación entre conjuntos: la diferencia simétrica. Abordaremos este tema demostrando algunos resultados con ayuda del álgebra de conjuntos. Algunos otros los probaremos con el método de demostración habitual.

Conceptos previos

Definición. Sean $A$ y $B$ conjuntos arbitrarios, definimos la diferencia simétrica de $A$ con $B$, como:

$A\triangle B= (A\setminus B)\cup (B\setminus A)$.

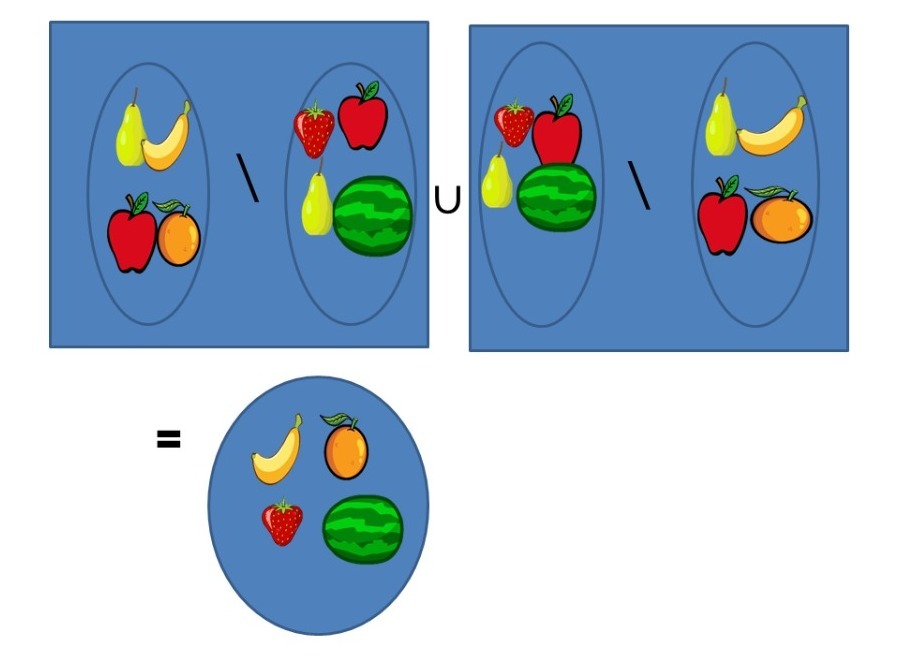
Ejemplo.

Consideremos $A=\set{\emptyset, \set{\emptyset}}$ y $B=\set{\emptyset, \set{\set{\emptyset}}}$. Tenemos que:

\begin{align*}
A\triangle B&=\set{\emptyset, \set{\emptyset}}\triangle\set{\emptyset,\set{\set{\emptyset}}}\\
&= (\set{\emptyset, \set{\emptyset}}\setminus\set{\emptyset,\set{\set{\emptyset}}})\cup (\set{\emptyset, \set{\set{\emptyset}}}\setminus\set{\emptyset,\set{\emptyset}}\\
&=\set{\set{\emptyset}}\cup\set{\set{\set{\emptyset}}}\\
&=\set{\set{\emptyset}, \set{\set{\emptyset}}}.
\end{align*}

$\square$

Si observamos con detalle el ejemplo anterior podremos notar que el conjunto que nos resulta también es igual a $(A\cup B)\setminus (A\cap B)$. De hecho, no solo ocurre para este caso en particular, sino que ocurre para cualesquiera conjuntos. Vamos a probarlo a continuación:

Proposición. Para cualesquiera $A, B$ conjuntos, se cumple que $A\triangle B=(A\cup B)\setminus (A\cap B)$.

Demostración.

\begin{align*}
A\triangle B&= (A\setminus B)\cup (B\setminus A)\\
&=(A\cap (X\setminus B))\cup (B\cap (X\setminus A))\\
&=(A\cup (B\cap(X\setminus A))\cap ((X\setminus B)\cup (B\cap(X\setminus A)))\\
&=((A\cup B)\cap(A\cup (X\setminus A)))\cap (((X\setminus B)\cup B)\cap ((X\setminus B)\cup(X\setminus A)))\\
&=((A\cup B)\cap X)\cap(X\cap (X\setminus (A\cap B))\\
&=(A\cup B)\cap (X\setminus(A\cap B))\\
&=(A\cup B)\setminus (A\cap B).
\end{align*}

$\square$

Otras equivalencias

Proposición. Sean $A$ y $B$ conjuntos. Sea $X$ un conjunto con respecto al cual tomaremos complementos. Se cumplen las siguientes igualdades de conjuntos:

1. $A\triangle B= (A\cap (X\setminus B))\cup (B\cap (X\setminus A))$,
2. $A\triangle B= (A\cup B)\cap (X\setminus(A\cap B))$.

Demostración.

1. 
   \begin{align*}
   (A\cap (X\setminus B))\cup(B\cap (X\setminus A))
   &=((A\cap (X\setminus B))\cup B)\cap((A\cap (X\setminus B))\cup (X\setminus A))\\
   &=(A\cap (X\setminus B))\cup B)\cap((A\cup (X\setminus A))\cap ((X\setminus B)\cup (X\setminus A)))\\
   &=(A\cap (X\setminus B))\cup B)\cap(X\cap ((X\setminus B)\cup (X\setminus A)))\\
   &=(A\cap (X\setminus B))\cup B)\cap((X\setminus B)\cup (X\setminus A))\\
   &=(A\cap (X\setminus B))\cup B)\cap(X\setminus (B\cap A))\\
   &=((A\cup B)\cap ((X\setminus B)\cup B))\cap (X\setminus (B\cap A))\\
   &=((A\cup B)\cap X)\cap (X\setminus (B\cap A))\\
   &=(A\cup B)\setminus (A\cap B)\\
   &=A\triangle B.
   \end{align*}
   
2. 
   \begin{align*}
   A\triangle B&= (A\cup B)\setminus (A\cap B)\\
   &=(A\cup B)\cap (X\setminus (A\cap B)).
   \end{align*}

$\square$

Propiedades de la diferencia simétrica

Veamos otras tres propiedades de la diferencia simétrica.

Proposición. Sean $A$ y $B$ conjuntos. Se satisfacen las siguientes propiedades:

1. $A\triangle \emptyset=A$,
2. $A\triangle A=\emptyset$,
3. $A\triangle B= B\triangle A$.

Demostración.

1. 
   \begin{align*}
   A\triangle \emptyset&= (A\setminus\emptyset)\cup (\emptyset\setminus A)\\
   &=A\cup \emptyset=A.
   \end{align*}
2. 
   \begin{align*}
   A\triangle A&= (A\setminus A)\cup (A\setminus A)\\
   &=\emptyset\cup \emptyset\\
   &=\emptyset.
   \end{align*}
3. 
   \begin{align*}
   A\triangle B&= (A\setminus B)\cup (B\setminus A)\\
   &=(B\setminus A)\cup (A\setminus B)\\
   &=B\triangle A.
   \end{align*}

$\square$

Proposición. $A\triangle B=\emptyset$ si y sólo si $A=B$.

Demostración.

Supongamos primero que $A=B$, entonces $A\triangle B= (A\setminus B)\cup (B\setminus A)= (A\setminus A)\cup (A\setminus A)=\emptyset\cup \emptyset=\emptyset$.

Por otro lado, si $A\triangle B=\emptyset$, tenemos que $(A\setminus B)\cup (B\setminus A)= \emptyset$. Esto implica que $A\setminus B=\emptyset=B\setminus A$ pues de otra forma la unión de estos conjuntos no resultaría ser el conjunto vacío.
Por un lado, $A\setminus B=\emptyset$ implica que $A\subseteq B$ y $B\setminus A=\emptyset$ implica que $B\subseteq A$. Por lo tanto, $A=B$.

$\square$

Tarea moral

Para $A$, $B$ y $C$ conjuntos, demuestra que se satisfacen las siguientes propiedades:

1. $A\cap (B\triangle C)=(A\cap B)\triangle (A\cap C)$.
2. Si $A\triangle B= A\triangle C$, entonces $B=C$.
3. $A\triangle (B\triangle C)=(A\triangle B)\triangle C$.

Más adelante…

En la siguiente entrada introduciremos nuevos conceptos: definiremos qué es un par ordenado y a partir de éste concepto definiremos al producto cartesiano. Será necesario que recuerdes el concepto de par no ordenado. (Ver Teoría de los Conjuntos I: Axioma de unión y axioma de par).

Entradas relacionadas

• Entrada relacionada: Teoría de los Conjuntos I: Álgebra de conjuntos de esta entrada podrás apoyarte para seguir los pasos de las demostraciones que hicimos en esta sección.
• Ir a Teoría de los Conjuntos I
• Entrada anterior: Teoría de los Conjuntos I: Álgebra de conjuntos
• Siguiente entrada: Teoría de los Conjuntos I: Parejas ordenadas y producto cartesiano

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE109323 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 3»