Introducción

En las entradas correspondientes a esta parte del curso aprenderemos varias técnicas que nos permitirán resolver problemas que involucren desigualdades. El área es enorme y hay libros enteros dedicados a ello. Nosotros sólo veremos algunas técnicas. Comenzaremos con desigualdades básicas y nos enfocaremos en los siguientes temas:

• Desigualdad $x^2\ge 0$ y desigualdad del triángulo
• Desigualdades de medias
• La desigualdad de Cauchy-Schwarz
• Técnicas de cálculo en desigualdades

En esta entrada veremos el primer inciso, que consiste de dos ideas muy sencillas:

Desigualdad $x^2\ge 0$. El cuadrado de cualquier número real es mayor o igual a cero. Es cero si y sólo si el número es cero.

Desigualdad del triángulo. Si $V$ es un espacio vectorial con norma $\Vert \cdot \Vert$, entonces para cualesquiera vectores $u$ y $v$ se tiene que $$\Vert u\Vert +\Vert v\Vert \ge \Vert u+v\Vert .$$

La desigualdad $x^2\ge 0$ parece muy inocente. Sin embargo, es una herramienta muy versátil cuando se combina con manipulaciones algebraicas creativas. La desigualdad del triángulo la estamos enunciando para espacios vectoriales con norma en general. Dos casos particulares que a lo mejor te son más familiares son los siguientes:

Desigualdad del triángulo para $\mathbb{R}$. Si $a$ y $b$ son números reales, entonces $|a|+|b|\ge |a+b|$.

Desigualdad del triángulo en ${\mathbb{R}}^n$. Si $ABC$ es un triángulo en el plano (o dimensiones más altas) , de lados de longitudes $\overline{AB}=c$, $\overline{BC}=a$ y $\overline{CA}=b$, entonces
$$\begin{array}{rl}a+b& \ge c\\ b+c& \ge a\\ c+a& \ge b.\end{array}$$

Si una de las igualdades se da, $ABC$ es un triángulo degenerado, es decir, con sus tres vértices alineados. En otro caso, todas las desigualdades son estrictas.

Veamos aplicaciones de estas desigualdades básicas.

La desigualdad $\frac{a^2+b^2}{2}\ge \sqrt{ab}$

Comenzaremos probando de dos formas distintas una desigualdad que también resulta útil en otras ocasiones.

Problema. Sean $a$ y $b$ números reales mayores o iguales a cero. Muestra que $$\frac{a+b}{2}\ge \sqrt{ab},$$ y que la igualdad se da si y sólo si $a$ y $b$ son iguales.

A esta desigualdad se le conoce como la desigualdad MA-MG para dos números reales. También forma parte de las desigualdades básicas que te ayudará conocer. Se llama así pues en el lado izquierdo tenemos a la media aritmética de los números $a$ y $b$, y al lado derecho tenemos la media geométrica de los números $a$ y $b$. En realidad la desigualdad se vale para más reales no negativos, pero esto lo veremos en otra entrada.

Sugerencia pre-solución. El problema se puede resolver tanto de manera algebraica, (usando $x^2\ge 0$) como de manera geométrica (usando la desigualdad del triángulo).

Para resolverlo de la primera forma, trabaja hacia atrás. Haz manipulaciones algebraicas para formular problemas equivalentes hasta que llegues a una desigualdad obvia.

Para resolverlo de la segunda forma, haz una figura en la que puedas representar tanto a la media geométrica como a la aritmética. Una forma de hacerlo es comenzar con una semicircunferencia de diámetro $a+b$.

Para identificar el caso de igualdad, haz un análisis de casos.

Solución algebraica. Queremos mostrar que $$\frac{a+b}{2}\ge \sqrt{ab}.$$ Pasando el dos multiplicando, y luego $2\sqrt{ab}$ restando al lado izquierdo, esta desigualdad igualdad ocurre si y sólo si $$a+b-2\sqrt{ab}\ge 0.$$ En el lado izquierdo identificamos un binomio al cuadrado, que se puede factorizar para dar la desigualdad equivalente $${(\sqrt{a}-\sqrt{b})}^2\ge 0.$$

Esta desigualdad es de la forma $x^2\ge 0$, así que es claramente cierta. La igualdad ocurre si y sólo si $\sqrt{a}-\sqrt{b}=0$, lo cual sucede si y sólo si $a=b$. Todos los pasos que hicimos son reversibles. Esto termina la solución.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fb.svg">}$

Solución geométrica. Consideremos la siguiente figura, en donde tenemos una semicircunferencia de diámetro $\overline{AB}=a+b$ y centro $O$. Aquí $C$ es un punto en $AB$ tal que $\overline{AC}=a$ y entonces $\overline{CB}=b$. Además, $D$ es un punto sobre la circunferencia tal que $DC$ es perpendicular a $AB$. Llamemos $d=\overline{CD}$.

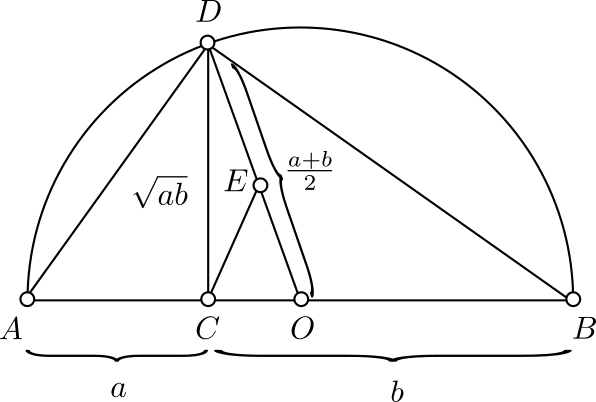
Como $\mathrm{△}AOD$ y $\mathrm{△}BOD$ son isósceles por tener dos lados iguales al radio de la circunferencia, tenemos que $\mathrm{\angle }ADO=\mathrm{\angle }DAO$ y $\mathrm{\angle }BDO=\mathrm{\angle }DBO$. Usando estas igualdades y que la suma de los ángulos internos de $\mathrm{△}ABD$ es ${180}^{\circ }$, se puede mostrar que el ángulo $ADB$ es de ${90}^{\circ }$.

De este modo, $\mathrm{△}ACD$ y $\mathrm{△}DCB$ son semejantes (por ser ambos semejantes a $\mathrm{△}ABD$ por criterio AA). Por la semejanza, tenemos que $$\frac{a}{d}=\frac{d}{b},$$ de donde $d=\sqrt{ab}$.

Para terminar la demostración, tomamos un punto $E$ sobre $DO$ tal que $\mathrm{\angle }EOC=\mathrm{\angle }ECO$. Por la desigualdad del triángulo en $\mathrm{△}DEC$, tenemos que

$$\begin{array}{rl}\sqrt{ab}& =\overline{DC}\\ & \le \overline{DE}+\overline{EC}\\ & =\overline{DE}+\overline{EO}\\ & =\overline{DO}\\ & =\frac{a+b}{2}.\end{array}$$

Con esto demostramos la desigualdad. Para terminar el problema, necesitamos ver cuándo se dan los casos de igualdad. Se tiene la igualdad si y sólo si $\mathrm{△}DEC$ es un triángulo degenerado, lo cual sucede si y sólo si $E$ está en el segmento $DC$. Esto sólo es posible cuando $DO$ es perpendicular a $AB$, lo cual sucede si y sólo si $C=O$, si y sólo si $AC=CB$, si y sólo si $a=b$.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fb.svg">}$

Desigualdades básicas aplicadas a un problema de la Olimpiada Mexicana de Matemáticas

El siguiente problema apareció como parte de los exámenes selectivos que el Comité Nacional de la Olimpiada Mexicana de Matemáticas envía a los estados para seleccionar a sus estudiantes en distintas etapas. Tiene muchas formas de resolverse, pero veamos cómo se puede resolver con desigualdades básicas.

Problema. Sean $a,b,c,d$ reales positivos con $a^2+b^2+c^2+d^2=4$. Muestra que $$a^5+b^5+c^5+d^5\ge a+b+c+d$$

Sugerencia pre-solución. Modifica el problema a mostrar como desigualdad auxiliar que para un real no negativo $x$ se tiene que $$x^5-2x^2-x+2\ge 0.$$ Esta desigualdad se puede demostrar usando que los cuadrados son no negativos.

Solución. Vamos a probar primero la desigualdad $$x^5-2x^2-x+2\ge 0.$$ Para que sea un poco más fácil, factorizaremos la expresión del lado izquierdo.

Notemos que $1$ es una raíz de $x^5-2x^2-x+2$, de modo que por el teorema del factor podemos factorizar $x-1$ del polinomio. Obtenemos que $$x^5-2x^2-x+2=(x-1)(x^4+x^3+x^2-x-2).$$

Notemos que, nuevamente, $1$ es una raíz de $(x^4+x^3+x^2-x-2)$. Al factorizar $x-1$ de nuevo, obtenemos que $$x^5-2x^2-x+2=(x-1{)}^2(x^3+2x^2+3x+2).$$

Ya estamos listos para probar la desigualdad que queremos. Notemos que $(x-1{)}^2\ge 0$ y que $x^3+2x^2+3x+2$ es mayor o igual que cero para $x\ge 0$ pues es un polinomio con puros coeficientes positivos. Esto prueba la desigualdad auxiliar. Reescribiéndola, tenemos que $$x^5\ge 2x^2+x-2.$$ Aplicándola en esta forma a los cuatro reales positivos $a,b,c,d$ del problema, y usando que la suma de cuadardos es $4$, obtenemos que
$$\begin{array}{rl}{a}^5& +b^5+c^5+d^5\\ & \ge 2(a^2+b^2+c^2+d^2)+a+b+c+d-8\\ & =2\cdot 4+a+b+c+d-8\\ & =a+b+c+d.\end{array}$$

Esto termina el problema.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fb.svg">}$

El primer paso parece un poco artificial. ¿Por qué queremos probar esa desigualdad auxiliar? En otra entrada de blog escribí cómo se puede llegar a las ideas de esta solución.

Desigualdad del triángulo aplicada a la construcción de tetraedros

Si pegamos cuatro triángulos equiláteros en el espacio se hace un tetraedro regular. De manera similar, si pegamos cuatro triángulos como el siguiente, también se hace un tetraedro en el espacio:

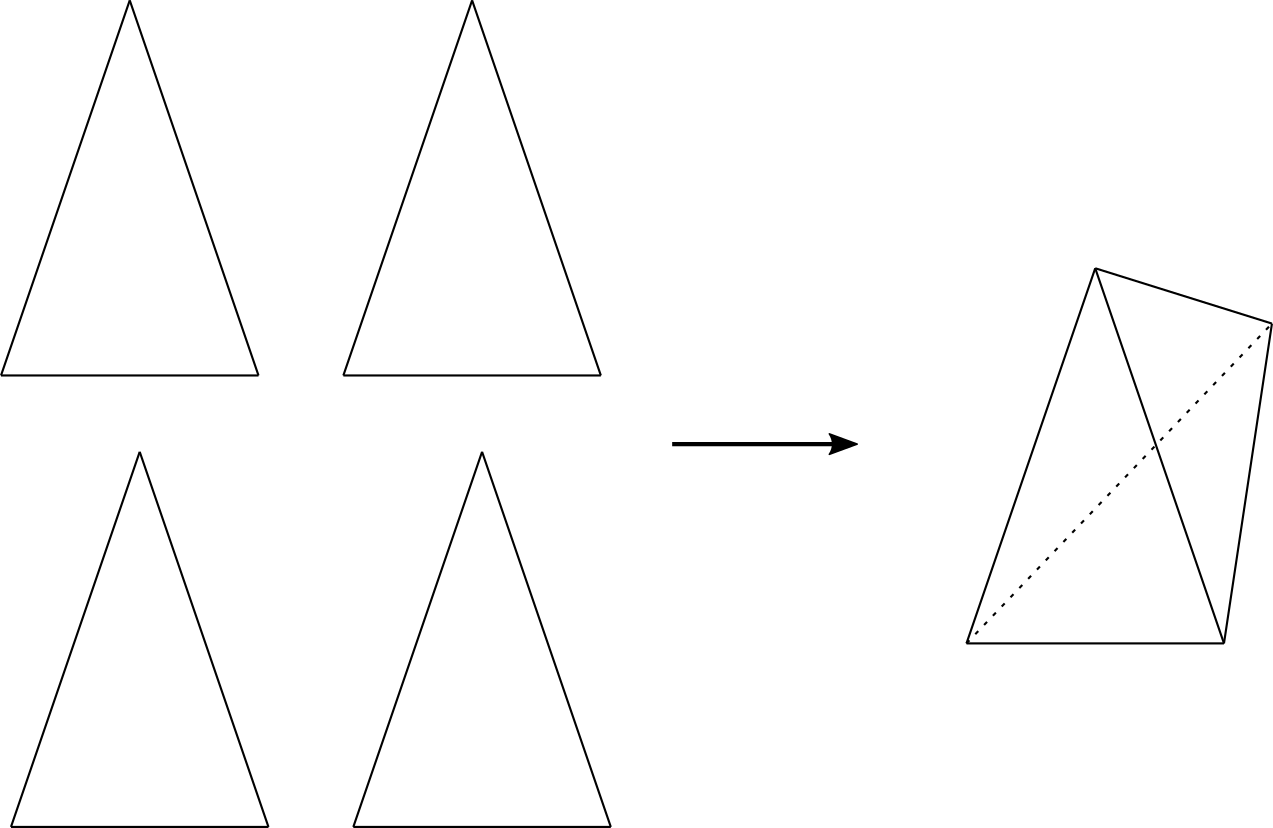
La intuición nos dice que debería poderse con cualquier triángulo. Pero esta intuición está mal.

Problema. Sea $ABC$ un triángulo con un ángulo mayor a ${90}^{\circ }$. Muestra que no existe ningún tetraedro en el espacio tal que sus cuatro caras sean congruentes a $ABC$.

Sugerencia pre-solución. Procede por contradicción. Por simetría, puedes asumir que el ángulo mayor a ${90}^{\circ }$ es el ángulo en $A$. Usa como punto auxiliar al punto medio de $BC$ y usa desigualdades.

Solución. Una observación inicial es que si $ABC$ es un triángulo, $M$ es el punto medio de $BC$ y su ángulo interno en $A$ es mayor a ${90}^{\circ }$, entonces $2\overline{AM}<\overline{BC}$. Esto se muestra trazando una circunferencia de diámetro $BC$.

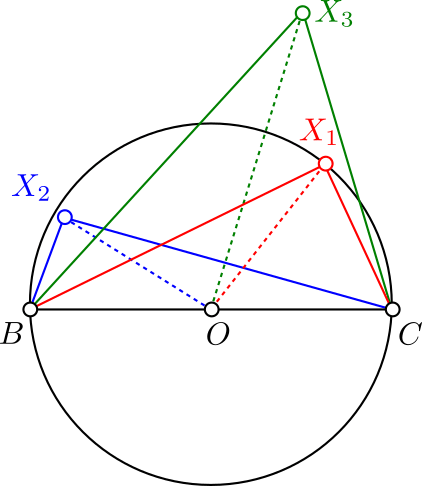
De hecho,

• Un punto $X$ está sobre la circunfencia si y sólo si $\mathrm{\angle }BXC={90}^{\circ }$, si y sólo si $\overline{OX}=\overline{OA}$.
• $X$ está dentro de la circunferencia si y sólo si $\mathrm{\angle }BXC>{90}^{\circ }$, si y sólo si $\overline{OX}<\overline{OA}$ y
• $X$ está fuera de la circunferencia si y sólo si $\mathrm{\angle }BXC<{90}^{\circ }$, si y sólo si $\overline{OX}>\overline{OA}$.

Resolvamos el problema. Sin pérdida de generalidad, el ángulo en $A$ es mayor a ${90}^{\circ }$. Entonces $\overline{AM}<\frac{\overline{BC}}{2}$, de donde $2\overline{AM}<\overline{BC}$.

Supongamos que se pudiera hacer en el espacio un tetraedro $WXYZ$ tal que cada una de las caras es congruente al triángulo $ABC$. Sin pérdida de generalidad, tenemos que
$$\begin{array}{rl}\overline{WX}& =\overline{YZ}=\overline{AB}\\ \overline{XY}& =\overline{ZW}=\overline{BC}\\ \overline{WY}& =\overline{XZ}=\overline{CA}.\end{array}$$

Tomemos el punto medio $M$ de $XY$. En $\mathrm{△}ZMW$, tenemos que
$$\begin{array}{rl}\overline{ZM}& =\overline{AM}\\ \overline{WM}& =\overline{AM}.\end{array}$$

Así, usando la desigualdad del triángulo en $\mathrm{△}ZMW$ tenemos que $$\begin{array}{rl}2\overline{AM}& =\overline{ZM}+\overline{WM}\\ & \ge \overline{ZW}\\ & =\overline{BC}.\end{array}$$

Esto es una contradicción con la desigualdad $2\overline{AM}<\overline{BC}$ que ya habíamos mostrado.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fb.svg">}$

Más problemas

Puedes encontrar más problemas de desigualdades básicas en la sección 7.1 del libro Problem Solving through Problems de Loren Larson. También puedes consultar más técnicas y problemas en el libro Desigualdades de la Olimpiada Mexicana de Matemáticas.