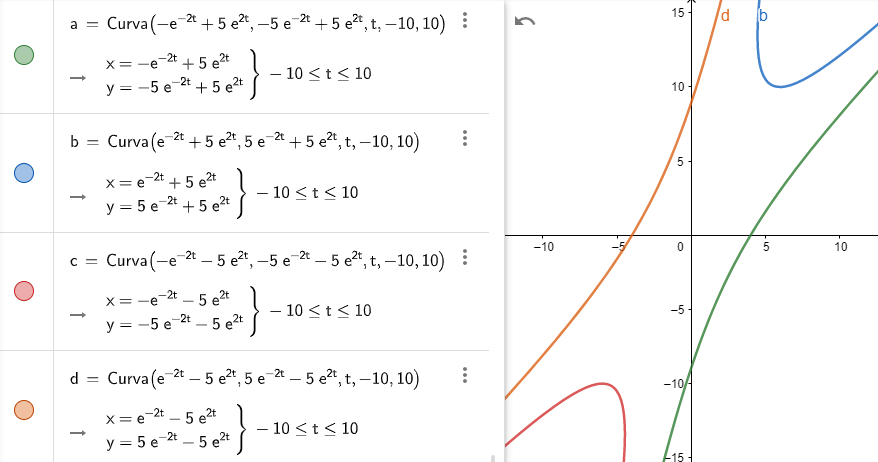Un matemático es un hombre ciego en un cuarto oscuro
tratando de buscar a un gato negro que no está allí.
– Charles Darwin
Introducción
En esta entrada concluiremos con el estudio cualitativo de los sistemas lineales homogéneos compuestos por dos ecuaciones diferenciales.
Hasta ahora somos capaces de clasificar y esbozar el comportamiento de las soluciones para los casos en los que los valores propios son reales, complejos y repetidos. Es momento de estudiar el último caso en donde uno o ambos de los valores propios son cero. Este caso es importante ya que divide los sistemas lineales con valores propios estrictamente positivos (repulsores) y valores propios estrictamente negativos (atractores) de aquellos que poseen un valor propio positivo y uno negativo (puntos silla).
Los casos posibles son
- $\lambda_{1} = 0$ y $\lambda_{2} < 0$.
- $\lambda_{1} = 0$ y $\lambda_{2} > 0$.
- $\lambda_{1} = \lambda_{2} = 0$.
Recordemos que el sistema que estamos estudiando es de la forma
\begin{align*}
x^{\prime} &= ax + by \\
y^{\prime} &= cx + dy \label{1} \tag{1}
\end{align*}
Este sistema lo podemos escribir como
$$\mathbf{Y}^{\prime} = \mathbf{AY} \label{2} \tag{2}$$
en donde,
$$\mathbf{Y}^{\prime} = \begin{pmatrix}
x^{\prime} \\ y^{\prime}
\end{pmatrix}, \hspace{1cm} \mathbf{Y} = \begin{pmatrix}
x \\ y
\end{pmatrix} \hspace{1cm} y \hspace{1cm} \mathbf{A} = \begin{pmatrix}
a & b \\ c & d
\end{pmatrix}$$
Sean $\lambda_{1}$ y $\lambda_{2}$ los valores propios de $\mathbf{A}$ y sean $\mathbf{K}_{1}$ y $\mathbf{K}_{2}$ los vectores propios de $\mathbf{A}$ asociados a cada valor propio, respectivamente.
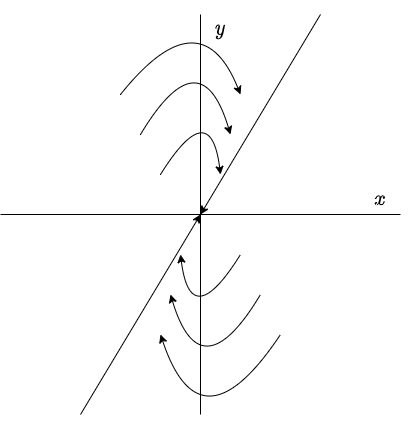
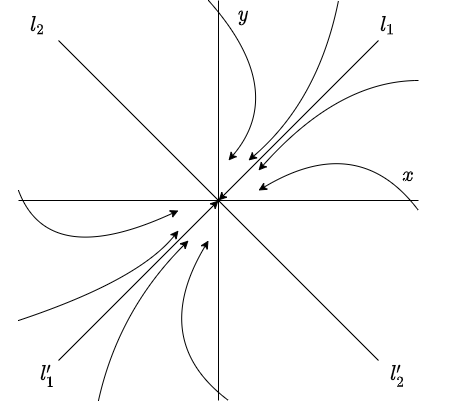
Comencemos por revisar el caso en el que un valor propio es nulo y el otro negativo.
Un valor propio nulo y otro negativo
Caso 1: $\lambda_{1} = 0$ y $\lambda_{2} < 0$.
Supongamos que $\lambda_{1} = 0$ y $\lambda_{2} < 0$ son los valores propios de $\mathbf{A}$. Debido a que $\lambda_{1} = 0$ y $\lambda_{2} \neq 0$, es decir, los valores propios son reales y distintos, entonces la solución general de (\ref{1}) debe ser de la forma
$$\mathbf{Y}(t) = c_{1} e^{\lambda_{1} t} \mathbf{K}_{1} + c_{2} e^{\lambda_{2} t} \mathbf{K}_{2} \label{3} \tag{3}$$
Pero $\lambda_{1} = 0$, por consiguiente la solución general es
$$\mathbf{Y}(t) = c_{1} \mathbf{K}_{1} + c_{2} e^{\lambda_{2} t} \mathbf{K}_{2} \label{4} \tag{4}$$
Observemos que esta solución depende de $t$ sólo a través del segundo término, de manera que si $c_{2} = 0$, entonces la solución será el vector constante
$$\mathbf{Y}(t) = c_{1} \mathbf{K}_{1} \label{5} \tag{5}$$
En este caso, todos los puntos $c_{1} \mathbf{K}_{1}$, para cualquier $c_{1}$, son puntos de equilibrio y todo aquel que esté situado en la línea de vectores propios para el valor propio $\lambda_{1} = 0$ es un punto de equilibrio.
Si $\lambda_{2} < 0$, entonces el segundo término en la solución general (\ref{4}) tiende a cero cuando $t$ crece, por lo que dicha solución tiende al punto de equilibrio $c_{1} \mathbf{K}_{1}$ a lo largo de una línea paralela a $\mathbf{K}_{2}$.
El plano fase indicando estas características es el siguiente.
Veamos que ocurre si $\lambda_{2} > 0$.
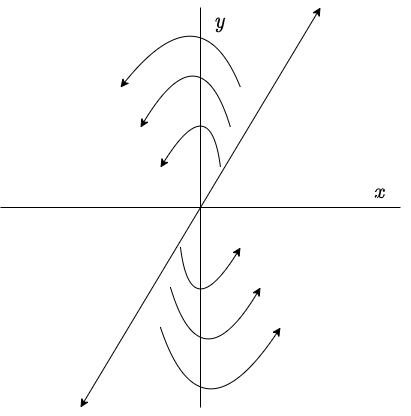
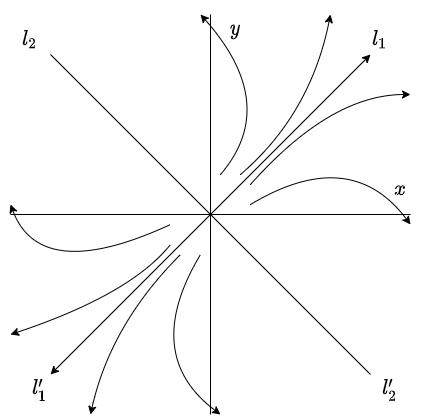
Un valor propio nulo y otro positivo
Caso 2: $\lambda_{1} = 0$ y $\lambda_{2} > 0$.
La solución general del sistema (\ref{1}) sigue siendo
$$\mathbf{Y}(t) = c_{1} \mathbf{K}_{1} + c_{2} e^{\lambda_{2} t} \mathbf{K}_{2}$$
Pero en este caso $\lambda_{2} > 0$, lo que implica que la solución se aleja de la línea de puntos de equilibrio cuando $t$ crece.
El plano fase es el siguiente.
Finalmente veamos que ocurre si $\lambda_{1} = \lambda_{2} = 0$.
Ambos valores propios nulos
Caso 3: $\lambda_{1} = \lambda_{2} = 0$.
En este caso ambos valores propios son repetidos, lo que significa que podemos aplicar la teoría vista en la entrada anterior. Sea $\mathbf{K}_{1}$ el único vector propio de la matriz $\mathbf{A}$ y sea $\mathbf{K}_{2}$ un vector propio generalizado de $\mathbf{A}$. Sabemos que la solución general del sistema (\ref{1}) en el caso de valores propios repetidos es
$$\mathbf{Y}(t) = c_{1} e^{\lambda t} \mathbf{K}_{1} + c_{2} e^{\lambda t} \left[ \mathbf{K}_{2} + t(\mathbf{A} -\lambda \mathbf{I}) \mathbf{K}_{2} \right] \label{6} \tag{6}$$
Sin embargo $\lambda = 0$, entonces la solución anterior se reduce a
$$\mathbf{Y}(t) = c_{1} \mathbf{K}_{1} + c_{2} \left[ \mathbf{K}_{2} + t \mathbf{A} \mathbf{K}_{2} \right] \label{7} \tag{7}$$
El hecho de que los valores propios sean nulos un vector propio podrá ser algún vector canónico
$$\mathbf{K} = \begin{pmatrix}
1 \\ 0
\end{pmatrix} \hspace{1cm} o \hspace{1cm} \mathbf{K} = \begin{pmatrix}
0 \\ 1
\end{pmatrix}$$
Las consecuencias de esto es que terminaremos con una solución en la que sólo una función $x(t)$ o $y(t)$ dependerá de $t$, mientras que la otra será una constante.
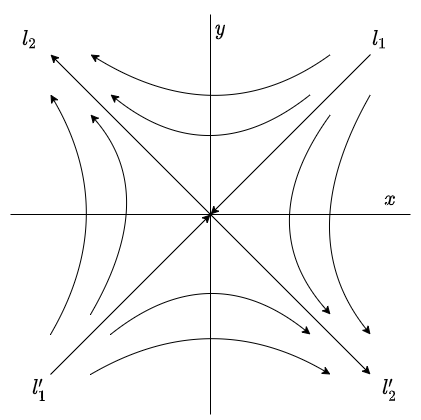
Supongamos que sólo $x$ depende de $t$, es decir, $x = x(t)$ y $y(t) = c$, con $c$ una constante, entonces para todo $t$ la función $y(t)$ tendrá el mismo valor, mientras que $x(t)$ dependerá de $t$ linealmente, esto en el plano fase se traduce en rectas paralelas al eje $X$ (ya que $y$ no cambia). La dirección de las trayectorias dependerá del signo de la constante que acompaña a la función $y(x)$.
El plano fase para el caso en el $x$ depende de $t$ es
Si se presenta el caso en el que $x(t)$ es una constante y $y(t)$ depende de $t$, entonces las trayectorias serán rectas verticales paralelas al eje $Y$.
En este caso los puntos de equilibrio del sistema serán el eje $X$ o el eje $Y$ dependiendo de que función sea la que dependa de $t$.
Concluyamos esta entrada con un ejemplo por cada caso visto.
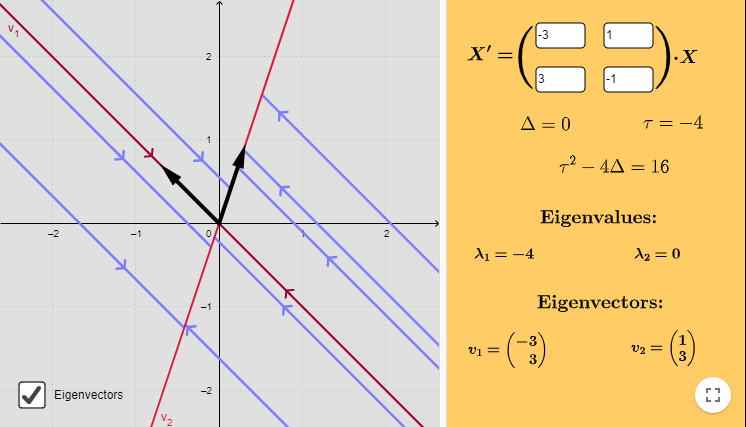
Caso 1: $\lambda_{1} = 0$ y $\lambda_{2} < 0$.
Ejemplo: Resolver el siguiente sistema lineal y hacer un análisis cualitativo de las soluciones.
$$\mathbf{Y}^{\prime} = \begin{pmatrix}
-3 & 1 \\ 3 & -1
\end{pmatrix} \mathbf{Y}$$
Solución: Determinemos los valores propios.
$$\begin{vmatrix}
-3 -\lambda & 1 \\ 3 & -1 -\lambda
\end{vmatrix} = \lambda (\lambda -4) = 0$$
Las raíces son $\lambda_{1} = 0$ y $\lambda_{2} = -4$. El vector propio asociado a $\lambda_{1} = 0$ lo obtenemos del siguiente sistema.
$$(\mathbf{A} -0 \mathbf{I}) \mathbf{K} = \mathbf{AK} = \begin{pmatrix}
-3 & 1 \\ 3 & -1
\end{pmatrix} \begin{pmatrix}
k_{1} \\ k_{2}
\end{pmatrix} = \begin{pmatrix}
0 \\ 0
\end{pmatrix}$$
Vemos que $3k_{1} = k_{2}$. Elegimos $k_{1} = 1$, tal que $k_{2} = 3$. El primer vector propio es
$$\mathbf{K}_{1} = \begin{pmatrix}
1 \\ 3
\end{pmatrix}$$
Determinemos el segundo vector propio asociado a $\lambda_{2} = -4$.
$$(\mathbf{A} + 4 \mathbf{I}) \mathbf{K} = \begin{pmatrix}
1 & 1 \\ 3 & 3
\end{pmatrix} \begin{pmatrix}
k_{1} \\ k_{2}
\end{pmatrix} = \begin{pmatrix}
0 \\ 0
\end{pmatrix}$$
En este caso $k_{1} = -k_{2}$. Sea $k_{1} = -3$, tal que $k_{2} = 3$. El segundo vector propio es
$$\mathbf{K}_{2} = \begin{pmatrix}
-3 \\ 3
\end{pmatrix}$$
Por lo tanto, la solución general del sistema es
$$\mathbf{Y}(t) = c_{1} \begin{pmatrix}
1 \\ 3
\end{pmatrix} + c_{2} e^{-4t} \begin{pmatrix}
-3 \\ 3
\end{pmatrix}$$
O bien,
\begin{align*}
x(t) &= c_{1} -3c_{2}e^{-4t} \\
y(t) &= 3c_{1} + 3c_{2}e^{-4t}
\end{align*}
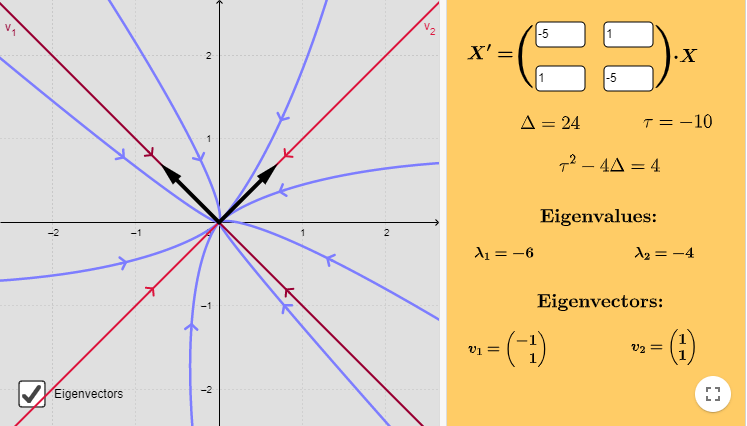
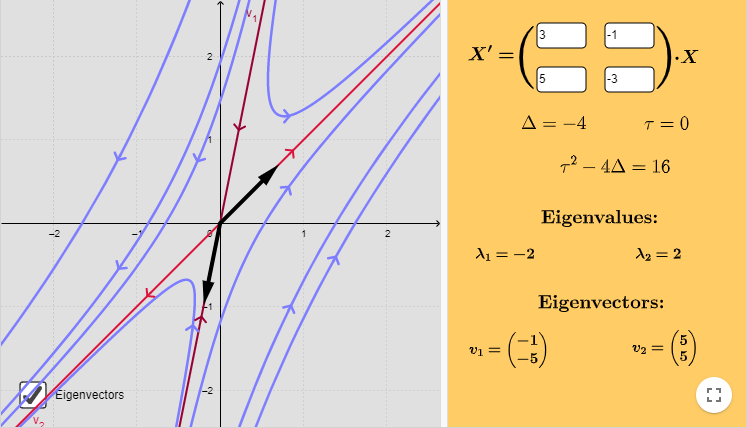
De acuerdo a la teoría vista, los puntos de equilibrio corresponden a la recta situada a lo largo del vector propio $\mathbf{K}_{1}$. Para encontrar esta recta consideremos que $c_{2} = 0$, de manera que la solución es
\begin{align*}
x(t) &= c_{1} \\
y(t) &= 3c_{1}
\end{align*}
De donde $y(x) = 3x$, por lo tanto, toda la recta $y = 3x$ contiene puntos de equilibrio.
Otra forma de verlo es a través de la definición. La función vectorial $F(x, y)$ en este caso es
$$F(x, y) = (-3x + y, 3x -y)$$
Los puntos de equilibrio son aquellos en los que $F(x, y) = (0, 0)$, es decir,
\begin{align*}
-3x + y &= 0 \\
3x -y &= 0
\end{align*}
De este sistema obtenemos que los puntos de equilibrio son aquellos en los que $3x = y$, es decir, la recta definida por la función $y(x) = 3x$.
Por otro lado, considerando nuevamente la solución general, es claro que
$$\lim_{t \to \infty} x(t) = c_{1} \hspace{1cm} y \hspace{1cm} \lim_{t \to \infty} y(t) = 3c_{1}$$
por lo que todas las trayectorias tienden a los puntos de equilibrio $c_{1}\mathbf{K}_{1}$ por cada valor de $c_{1}$ y lo hacen de forma paralela al vector propio $\mathbf{K}_{2}$.
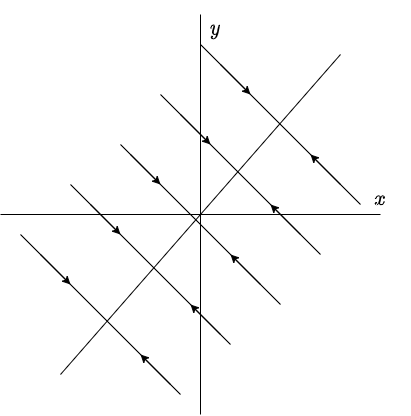
El plano fase indicando las características anteriores es el siguiente.
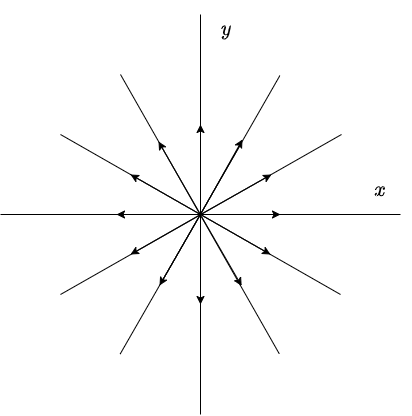
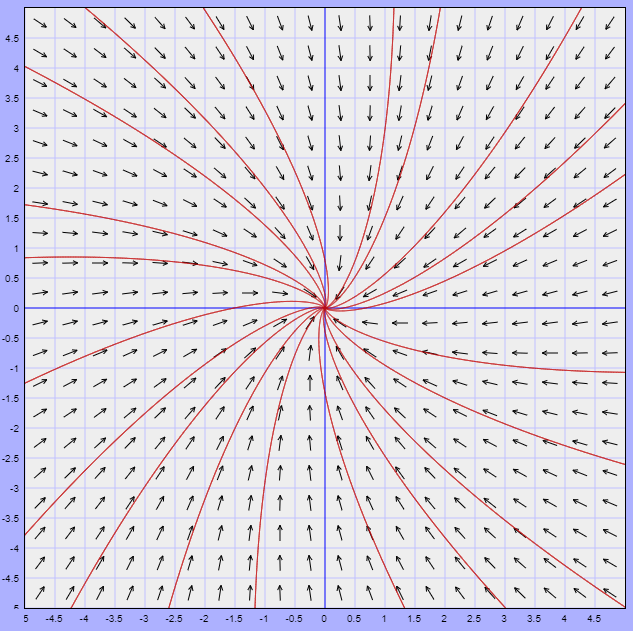
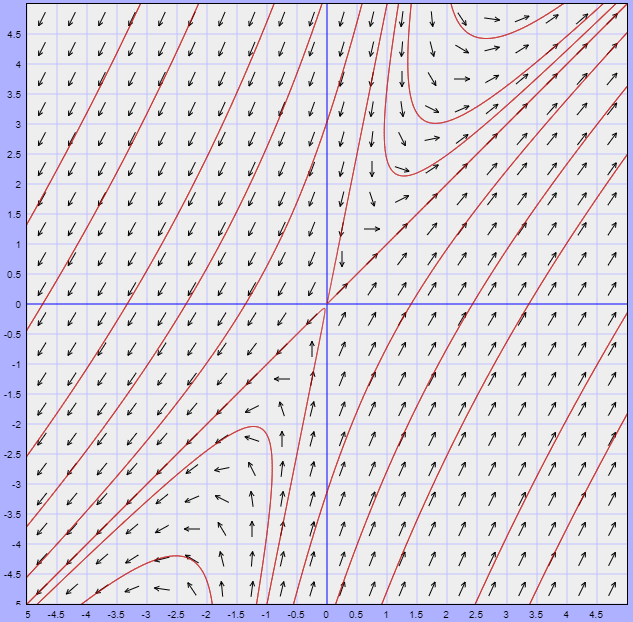
Ya vimos que la función vectorial es
$$F(x, y) = (-3x + y, 3x -y)$$
El campo vectorial definido por esta función, y algunas trayectorias correspondientes a soluciones del sistema, se muestran en la siguiente figura.
$\square$
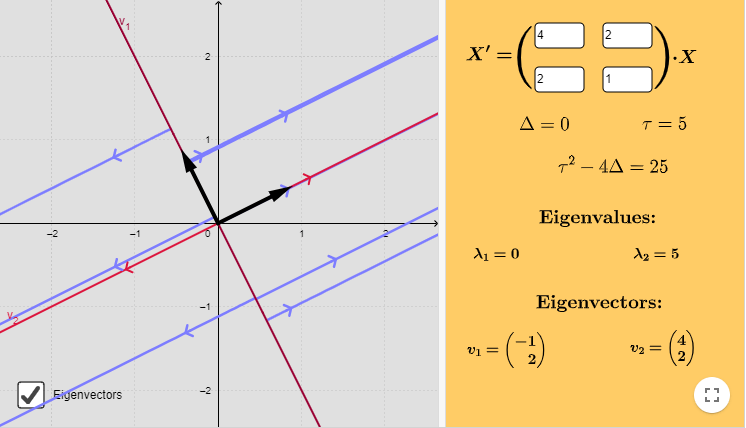
Caso 2: $\lambda_{1} = 0$ y $\lambda_{2} > 0$.
Ejemplo: Resolver el siguiente sistema lineal y hacer un análisis cualitativo de las soluciones.
$$\mathbf{Y}^{\prime} = \begin{pmatrix}
4 & 2 \\ 2 & 1
\end{pmatrix} \mathbf{Y}$$
Solución: Comencemos por determinar los valores propios.
$$\begin{vmatrix}
4 -\lambda & 2 \\ 2
& 1 -\lambda
\end{vmatrix} = \lambda (\lambda -5) = 0$$
Las raíces son $\lambda_{1} = 0$ y $\lambda_{2} = 5$. Determinemos primero el vector propio asociado al valor propio $\lambda_{1} = 0$.
$$(\mathbf{A} -0 \mathbf{I}) \mathbf{K} = \mathbf{AK} = \begin{pmatrix}
4 & 2 \\ 2 & 1
\end{pmatrix} \begin{pmatrix}
k_{1} \\ k_{2}
\end{pmatrix} = \begin{pmatrix}
0 \\ 0
\end{pmatrix}$$
De este sistema obtenemos que $2k_{1} = -k_{2}$. Sea $k_{1} = -1$, entonces $k_{2} = 2$. Por lo tanto, el primer vector propio es
$$\mathbf{K}_{1} = \begin{pmatrix}
-1 \\ 2
\end{pmatrix}$$
Determinemos el segundo vector propio asociado a $\lambda_{2} = 5$.
$$(\mathbf{A} -5 \mathbf{I}) \mathbf{K} = \begin{pmatrix}
-1 & 2 \\ 2 & -4
\end{pmatrix} \begin{pmatrix}
k_{1} \\ k_{2}
\end{pmatrix} = \begin{pmatrix}
0 \\ 0
\end{pmatrix}$$
Vemos que $2k_{2} = k_{1}$. Sea $k_{2} = 2$, entonces $k_{1} = 4$. Por lo tanto, el segundo vector propio es
$$\mathbf{K}_{2} =\begin{pmatrix}
4 \\ 2
\end{pmatrix}$$
Por lo tanto, la solución general del sistema es
$$\mathbf{Y}(t) = c_{1} \begin{pmatrix}
-1 \\ 2
\end{pmatrix} + c_{2}e^{5t} \begin{pmatrix}
4 \\ 2
\end{pmatrix}$$
O bien,
\begin{align*}
x(t) &= -c_{1} + 4c_{2}e^{5t} \\
y(t) &= 2c_{1} + 2c_{2}e^{5t}
\end{align*}
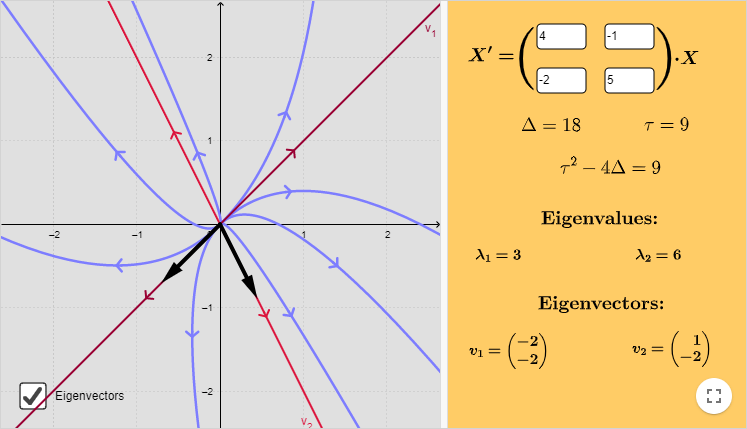
La recta que contiene a los puntos de equilibrio es aquella línea definida por el vector propio $\mathbf{K}_{1}$, es decir, si en la solución general hacemos $c_{2} = 0$, entonces obtenemos la solución
\begin{align*}
x(t) &= -c_{1} \\
y(t) &= 2c_{1}
\end{align*}
De donde obtenemos la función $y(x) = -2x$, todos los puntos de esta recta son puntos de equilibrio.
La función vectorial $F(x, y)$ en este caso es
$$F(x, y) = (4x + 2y, 2x + y)$$
Prueba que efectivamente si $y = -2x$, entonces $F(x, y) = (0, 0)$.
Por otro lado, de la solución general vemos que
$$\lim_{t \to -\infty} x(t) = -c_{1} \hspace{1cm} y \hspace{1cm} \lim_{t \to -\infty} y(t) = 2c_{1}$$
Y $x(t)$ y $y(t)$ divergen si $t \rightarrow \infty$, esto nos indica que las trayectorias se alejan de los puntos de equilibrio $c_{1} \mathbf{K}_{1}$ por cada valor de $c_{1}$ y lo hacen de forma paralela al vector propio $\mathbf{K}_{2}$.
El plano fase del sistema es el siguiente.
La función vectorial que define al campo vectorial asociado es
$$F(x, y) = (4x + 2y, 2x + y)$$
El campo vectorial y algunas trayectorias se muestran en la siguiente figura.
$\square$
Concluyamos con el caso especial en el que ambos valores propios son cero.
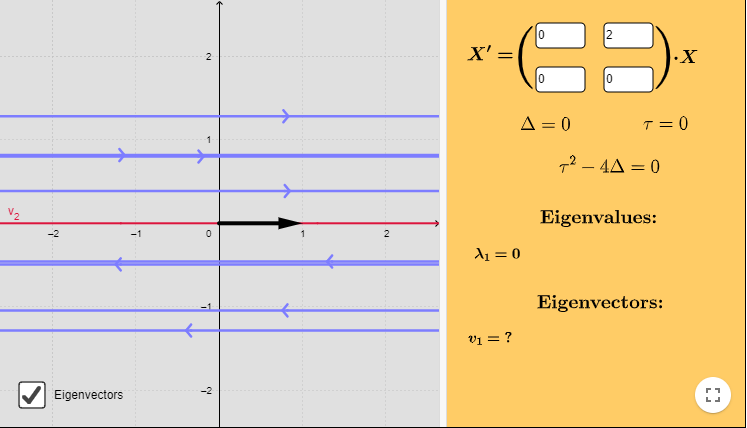
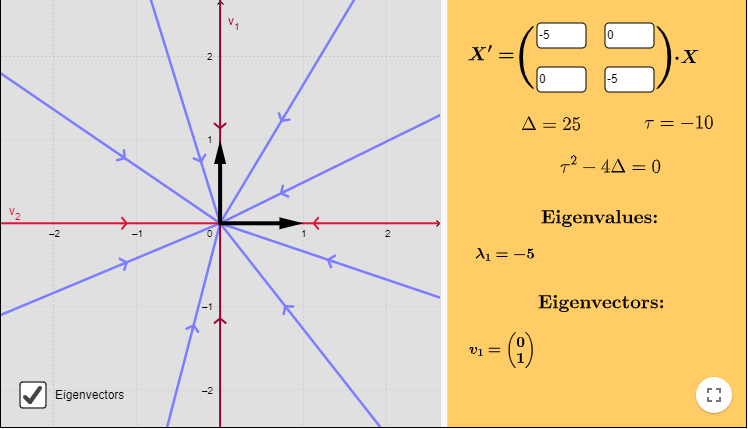
Caso 3: $\lambda_{1} = \lambda_{2} = 0$.
Ejemplo: Resolver el siguiente sistema lineal y hacer un análisis cualitativo de las soluciones.
$$\mathbf{Y}^{\prime} = \begin{pmatrix}
0 & 2 \\ 0 & 0
\end{pmatrix} \mathbf{Y}$$
Solución: Antes de comenzar a desarrollar el método notemos que se trata de un sistema muy sencillo, la ecuación de $y^{\prime}$ es
$$\dfrac{dy}{dt} = 0$$
Es claro que la solución es cualquier constante $C_{1}$, es decir $y(t) = C_{1}$, si sustituimos en la ecuación para $x^{\prime}$, tenemos
$$\dfrac{dx}{dt} = 2C_{1}$$
Resolviendo esta ecuación obtenemos la función
$$x(t) = 2C_{1}t + C_{2}$$
Por tanto, la solución general del sistema es
\begin{align*}
x(t) &= 2C_{1}t + C_{2} \\
y(t) &= C_{1}
\end{align*}
Vemos que sólo la función $x(t)$ depende de $t$, mientras que $y(t)$ es una constante.
Esto lo hacemos debido a que el sistema es bastante sencillo. Sin embargo, a continuación haremos el desarrollo hecho en la entrada anterior ya que, como veremos, los valores propios serán repetidos y nulos. Dichos valores propios los obtenemos de la siguiente ecuación característica.
$$\begin{vmatrix}
0 -\lambda & 2 \\ 0 & 0 -\lambda
\end{vmatrix} = \lambda^{2} = 0$$
La única raíz es $\lambda = 0$, es decir, cero es el único valor propio con multiplicidad $2$.
Para determinar el vector propio resolvemos el siguiente sistema.
$$\mathbf{AK} = \begin{pmatrix}
0 & 2 \\ 0 & 0
\end{pmatrix} \begin{pmatrix}
k_{1} \\ k_{2}
\end{pmatrix}$$
Este sistema nos indica que $2k_{2} = 0$, es decir, $k_{2} = 0$ y que $k_{1}$ puede tomar cualquier valor en $\mathbb{R}$. Tomemos $k_{1} = 1$, tal que el primer vector propio sea
$$\mathbf{K}_{1} = \begin{pmatrix}
1 \\ 0
\end{pmatrix}$$
Buscamos ahora un vector propio generalizado.
$$(\mathbf{A} -\lambda \mathbf{I})^{2} \mathbf{K} = \begin{pmatrix}
0 & 2 \\ 0 & 0
\end{pmatrix} \begin{pmatrix}
0 & 2 \\ 0 & 0
\end{pmatrix} \begin{pmatrix}
k_{1} \\ k_{2}
\end{pmatrix} = \begin{pmatrix}
0 & 0 \\ 0 & 0
\end{pmatrix} \begin{pmatrix}
k_{1} \\ k_{2}
\end{pmatrix} = \begin{pmatrix}
0 \\ 0
\end{pmatrix}$$
Debido a que cualquier vector $\mathbf{K}$, tal que
$$\mathbf{AK} \neq \mathbf{0}$$
es un vector propio generalizado, elegimos el vector ortogonal
$$\mathbf{K}_{2} = \begin{pmatrix}
0 \\ 1
\end{pmatrix}$$
Por lo tanto, la solución general es
\begin{align*}
\mathbf{Y}(t) &= c_{1} \begin{pmatrix}
1 \\ 0
\end{pmatrix} + c_{2} \left[ \begin{pmatrix}
1 \\ 0
\end{pmatrix} + t \begin{pmatrix}
0 & 2 \\ 0 & 0
\end{pmatrix} \begin{pmatrix}
0 \\ 1
\end{pmatrix} \right] \\
&= c_{1} \begin{pmatrix}
1 \\ 0
\end{pmatrix} + c_{2} \left[ \begin{pmatrix}
0 \\ 1
\end{pmatrix} + t
\begin{pmatrix}
2 \\ 0
\end{pmatrix} \right] \\
&= c_{1} \begin{pmatrix}
1 \\ 0
\end{pmatrix} + c_{2} \left[ \begin{pmatrix}
0 \\ 1
\end{pmatrix} + 2t
\begin{pmatrix}
1 \\ 0
\end{pmatrix} \right]
\end{align*}
Solución que podemos escribir como
\begin{align*}
x(t) &= c_{1} + 2c_{2}t \\
y(t) &= c_{2}
\end{align*}
Esta solución es la misma que encontramos antes. Debido a que $x(t)$ depende de $t$ linealmente, entonces por cada valor de $y(t)$, es decir de $c_{2}$, $x(t)$ tomará todos los valores en $\mathbb{R}$. Esto significa que en el plano fase las trayectorias serán rectas paralelas al eje $X$.
Verifica que los puntos de equilibrio del sistema corresponden al eje $X$ del plano fase.
Notemos que si $y(x) > 0$, o bien, $c_{2} > 0$, entonces
$$\lim_{t \to \infty} x(t) = \infty$$
y si $y(x) < 0$, o bien, $c_{2} < 0$, entonces
$$\lim_{t \to \infty} x(t) = -\infty$$
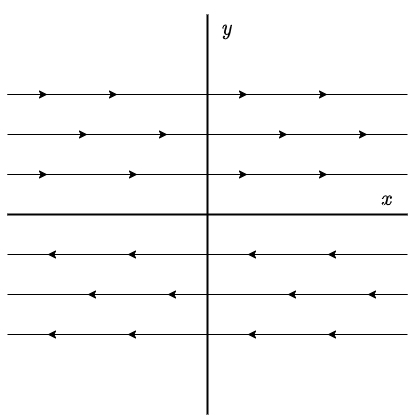
De manera que para $y > 0$ las trayectorias se moverán hacía la derecha y lo harán en sentido opuesto si $y < 0$. El plano fase es el siguiente.
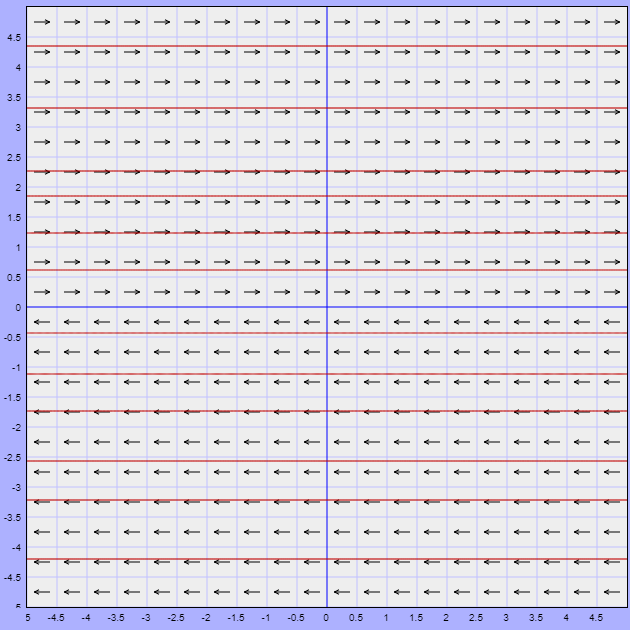
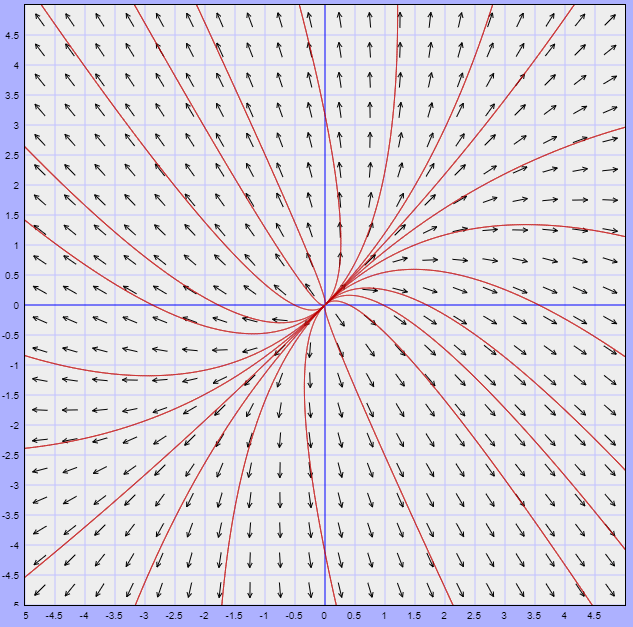
La función que define al campo vectorial es
$$F(x, y) = (2y, 0)$$
En la siguiente figura se muestra el campo vectorial asociado y algunas trayectorias.
$\square$
Hemos concluido con el estudio de los sistemas lineales.
Más adelante comenzaremos a estudiar sistemas no lineales, al menos desde una perspectiva cualitativa, y veremos que mucho de los que vimos en los casos lineales nos será de ayuda ya que los planos fase de los sistemas no lineales en la vecindad de un punto de equilibrio son, con frecuencia, muy similares a los planos fase de sistemas lineales, así que veremos esta conexión entre ambos sistemas.
Pero antes de estudiar a los sistemas no lineales dedicaremos la siguiente entrada en hacer un repaso de lo visto en las últimas 4 entradas y resumirlo en lo que se conoce como el plano traza – determinante, ya que seguramente en este punto podría parecernos que hay muchas posibilidades diferentes para los sistemas lineales.
Tarea moral
Los siguientes ejercicios no forman parte de la evaluación del curso, pero servirán para entender mucho mejor los conceptos vistos en esta entrada, así como temas posteriores.
- Resolver los siguientes sistemas lineales y hacer un análisis cualitativo de las soluciones.
- $\mathbf{Y}^{\prime} = \begin{pmatrix}
2 & 4 \\ 3 & 6
\end{pmatrix} \mathbf{Y}$
- $\mathbf{Y}^{\prime} = \begin{pmatrix}
-3 & 1 \\ 3 & -1
\end{pmatrix} \mathbf{Y}$
- $\mathbf{Y}^{\prime} = \begin{pmatrix}
0 & -3 \\ 0 & 0
\end{pmatrix} \mathbf{Y}$
- $\mathbf{Y}^{\prime} = \begin{pmatrix}
3 & 6 \\ -1 & -2
\end{pmatrix} \mathbf{Y}$
- $\mathbf{Y}^{\prime} = \begin{pmatrix}
-1 & 4 \\ 1/2 & -2
\end{pmatrix} \mathbf{Y}$
- $\mathbf{Y}^{\prime} = \begin{pmatrix}
0 & 0 \\ 5 & 0
\end{pmatrix} \mathbf{Y}$
Más adelante…
Hemos concluido con el análisis analítico y cualitativo de los sistemas lineales homogéneos compuestos por dos ecuaciones diferenciales del primer orden. Para tener todo en perspectiva, en la siguiente entrada haremos un breve repaso de todo lo visto con respecto a estos sistemas y resumiremos todo en un plano especial conocido como el plano traza – determinante.
Entradas relacionadas
- Página principal del curso: Ecuaciones Diferenciales I
- Entrada anterior del curso: Teoría cualitativa de los sistemas lineales homogéneos – Valores propios repetidos
- Siguiente entrada del curso: El plano Traza – Determinante
- Video relacionado al tema: Plano fase para sistemas lineales con cero como valor propio
Agradecimientos
Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»