Archivo de la etiqueta: segmentos dirigidos

Geometría Moderna II: Eje radical de 2 circunferencias

Por Armando Arzola Pérez

Deja un comentario

Introducción

En la entrada anterior hablamos de la noción de potencia de un punto con respecto a una circunferencia. Lo que haremos ahora es tomar dos circunferencias y preguntarnos por los puntos cuya potencia a ellas coincide. Esto nos llevará a estudiar la noción de eje radical de las circunferencias.

A grandes rasgos, definiremos qué es el eje radical. Luego, mostraremos que es una recta muy específica. Después de hacer eso, estudiaremos qué sucede si tenemos tres circunferencias. Finalmente, hablaremos un poco de cómo dibujar el eje radical de dos circunferencias.

Eje radical de 2 circunferencias

La definición que nos interesa estudiar ahora es el conjunto de puntos del plano cuyas potencias a dos circunferencias coincide. La siguiente definición formaliza esto.

Definición. El eje radical de dos circunferencias no concéntricas $\mathcal{C}_1$ y $\mathcal{C}_2$ es el lugar geométrico de los puntos $P$ tales que $$\text{Pot}(P,\mathcal{C}_1)=\text{Pot}(P,\mathcal{C}_2).$$ Si un punto está en el eje radical de ellas, decimos que es equipotente a ambas.

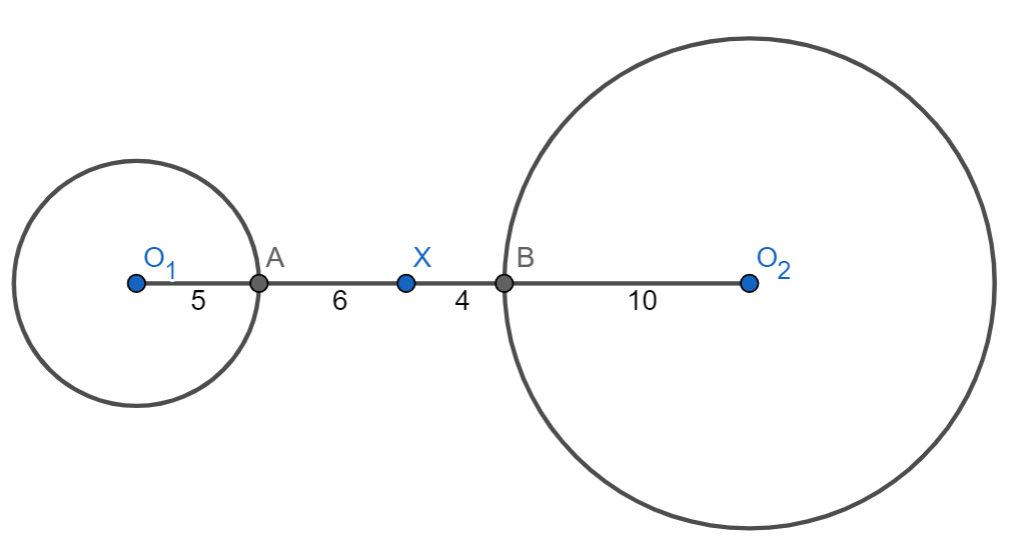
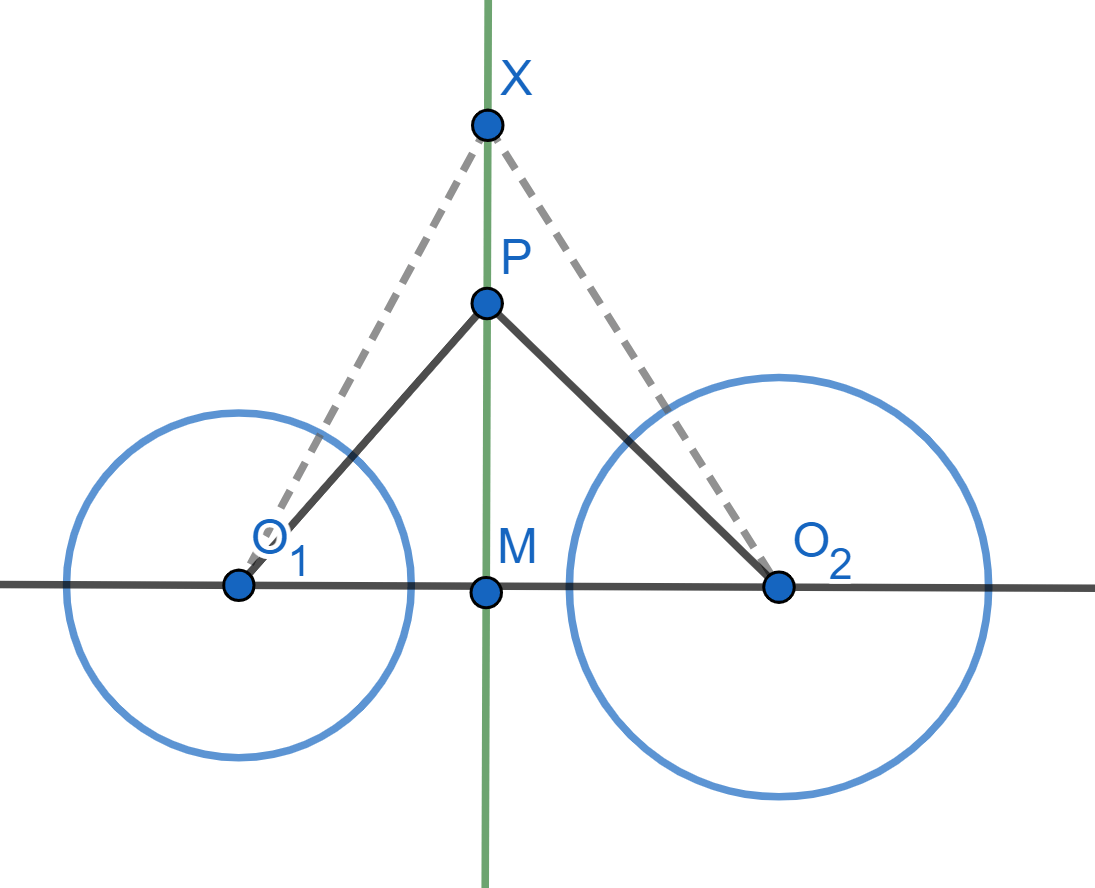
Ejemplo. Supongamos que tenemos dos circunferencias $\mathcal{C}_1$ y $\mathcal{C}_2$ de centros $O_1$ y $O_2$, y de radios $5$ y $10$ respectivamente. Supongamos que $|O_1O_2|=25$. El punto $X$ entre $O_1$ y $O_2$ que está a distancia $11$ de $O_1$ y a distancia $14$ de $O_2$ es equipotente a ambas circunferencias. Esto se debe a que su potencia a $\mathcal{C}_1$ es $(-6)(-16)=96$ y que su potencia a $\mathcal{C}_2$ es $(4)(24)=96$ también.

$\triangle$

El eje radical es una recta

En esta sección demostraremos el siguiente teorema.

Teorema. Sean $\mathcal{C}_1$ y $\mathcal{C}_2$ circunferencias no concéntricas de de centros $O_1$ y $O_2$. El eje radical de ellas es la recta que perpendicular a la recta $O_1O_2$, y que pasa por el punto $M$ de $O_1O_2$ que cumple $\text{Pot}(M,\mathcal{C}_1)=\text{Pot}(M,\mathcal{C}_2).$

La demostración de este teorema la dividiremos en las siguientes partes:

  1. Probar que existe al menos un punto $P$ en el eje radical.
  2. Mostrar que la proyección $M$ de dicho punto a la recta $O_1O_2$ también está en el eje radical.
  3. Ver que todo punto en la perpendicular a $O_1O_2$ por $M$ está en el eje radical.
  4. Mostrar que no existen otros puntos en el eje radical más allá de los ya localizados.

Veamos cada uno de estos puntos como una proposición por separado.

Proposición. Sean $\mathcal{C}_1$ y $\mathcal{C}_2$ circunferencias no concéntricas. Existe al menos un punto $P$ en el eje radical de $\mathcal{C}_1$ y $\mathcal{C}_2$.

Demostración. Vamos a dar una construcción explícita para encontrar un punto en el eje radical de $\mathcal{C}_1$ y $\mathcal{C}_2$:

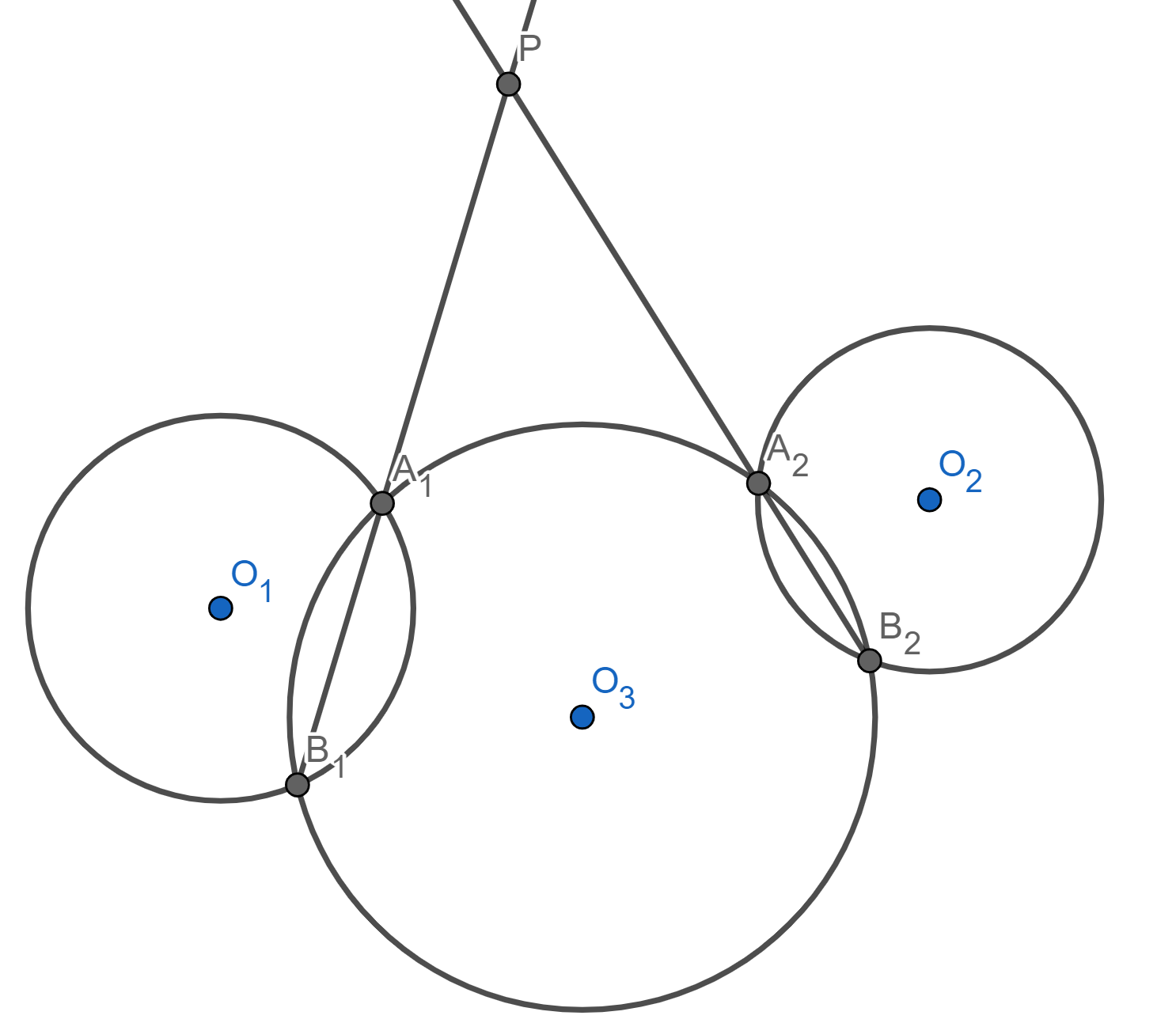
Eje radical de 2 circunferencias, construcción de un punto equipotente

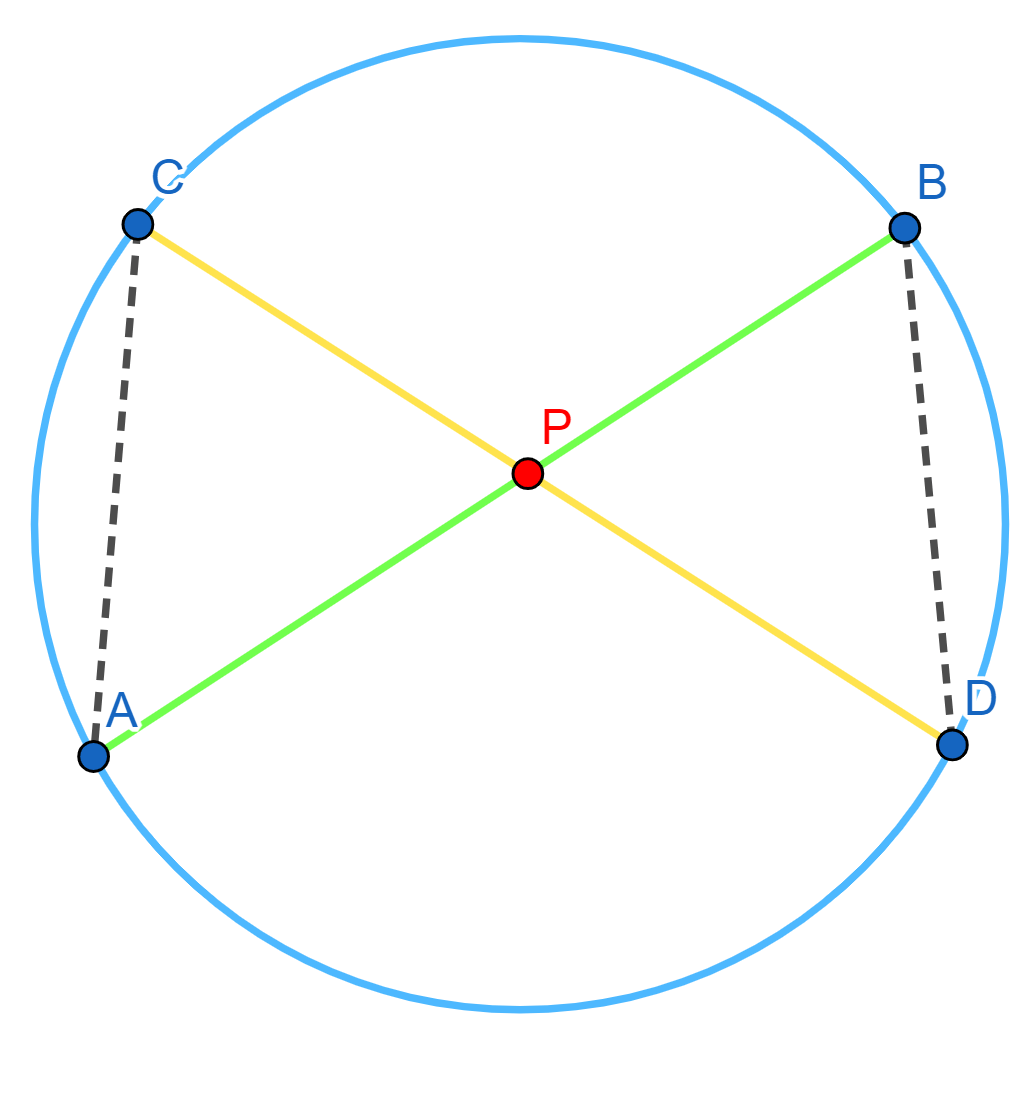
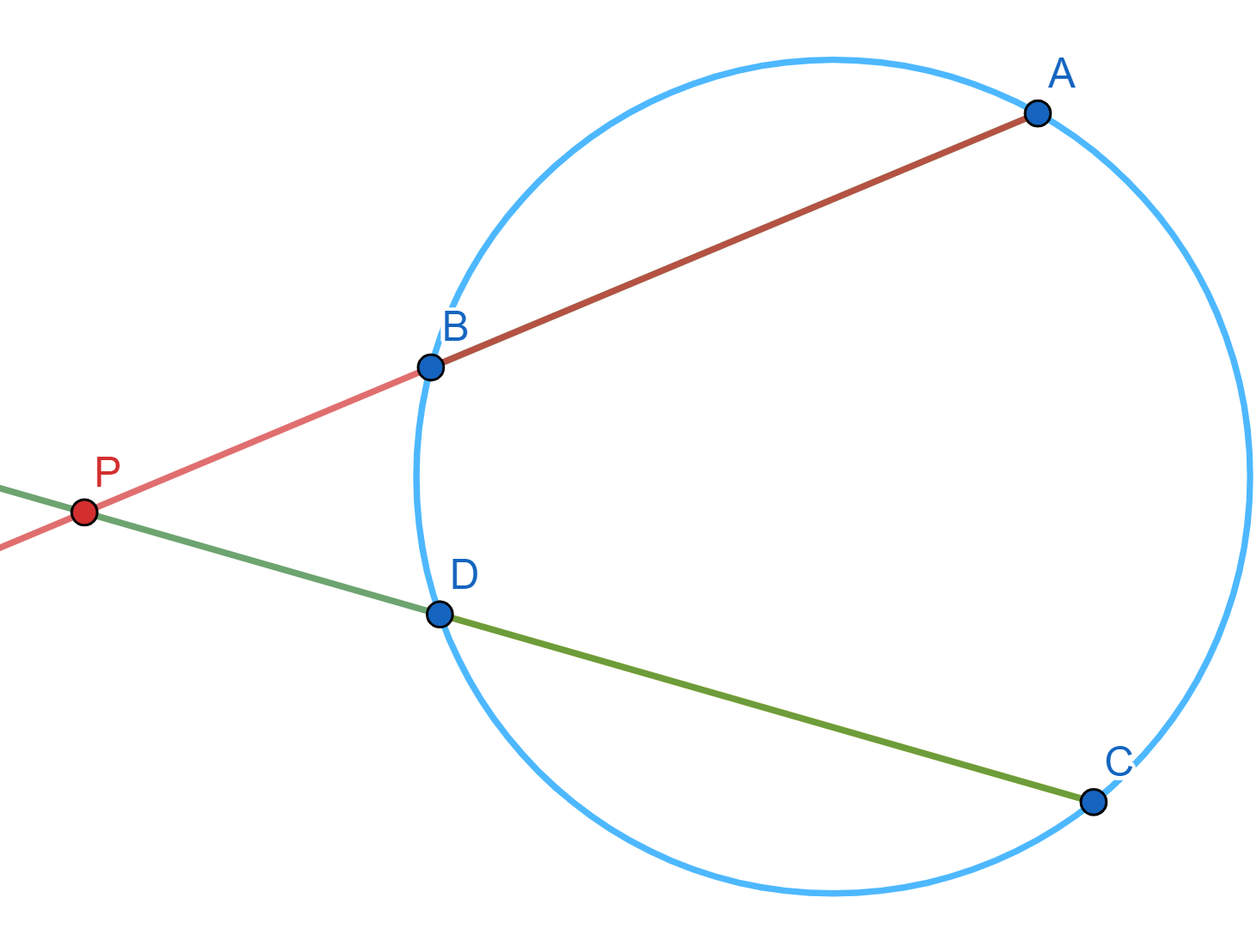
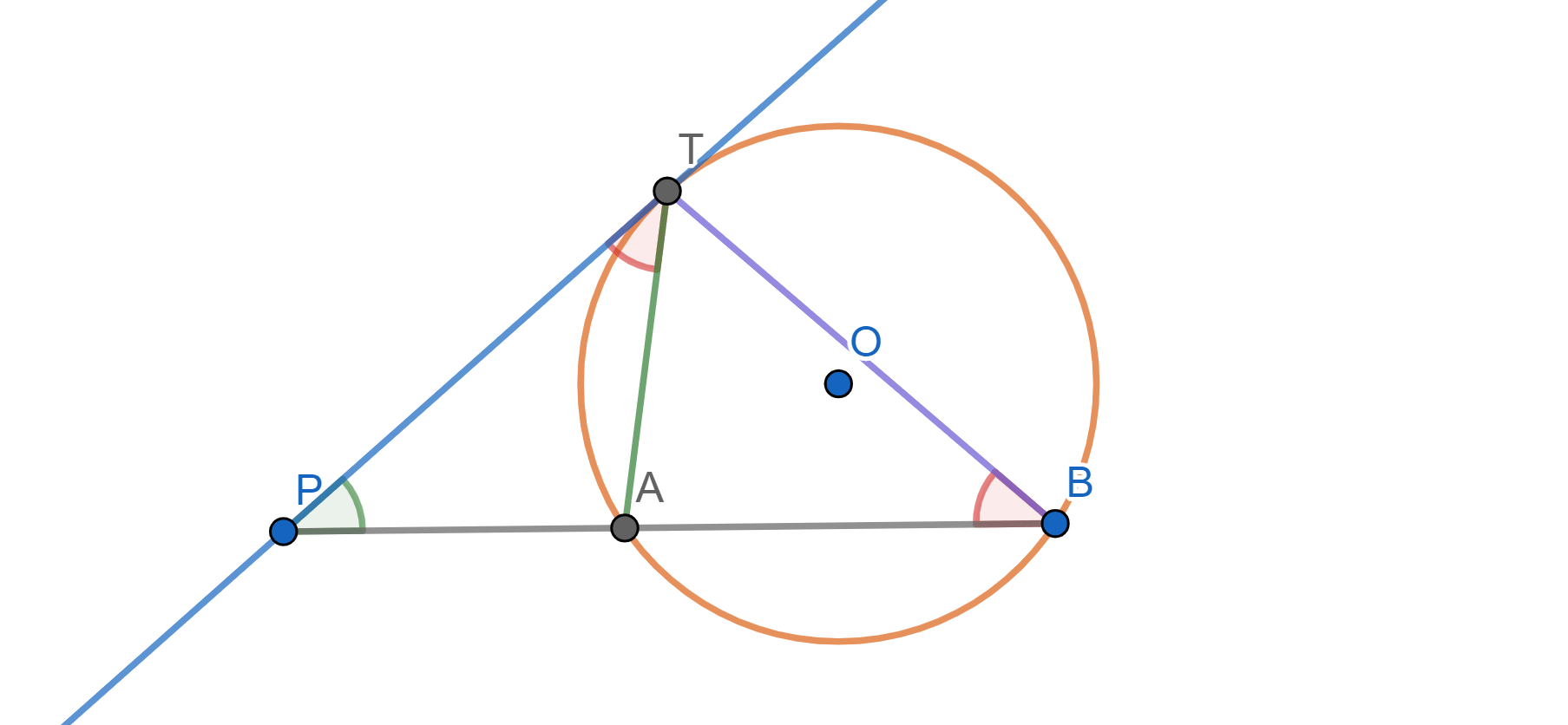
Para ello, tracemos una tercera circunferencia $\mathcal{C}_3$ que intersecte a cada una de $\mathcal{C}_1$ y $\mathcal{C}_2$ en dos puntos (una manera de hacer esto esto tomar $\mathcal{C}_3$ como el circuncírculo un punto dentro de $\mathcal{C}_1$, uno dentro de $\mathcal{C}_2$ y otro fuera de ambas).

Llamamos $A_1,B_1$ las intersecciones con $\mathcal{C}_1$ y $A_2,B_2$ las intersecciones con $\mathcal{C}_2$. Tomamos el punto $P$ como la intersección de $A_1B_1$ con $A_2B_2$ como en la siguiente figura.

Las siguientes cuentas muestran que $P$ es equipotente a ambas. Estamos usando el resultado de la entrada anterior que muestra que el cálculo de la potencia con respecto a $\mathcal{C}_3$ no depende de los puntos elegidos.

\begin{align*}
\text{Pot}(P,\mathcal{C}_1)&=PA_1 \cdot PB_1\\
&=\text{Pot}(P,\mathcal{C}_3)\\
&=PA_2 \cdot PB_2\\
&=\text{Pot}(P,\mathcal{C}_2).
\end{align*}

Por lo anterior, en efecto existe al menos un punto en el eje radical.

$\square$

Ahora veremos que la proyección de un punto equipotente en la recta de los centros también es un punto equipotente.

Proposición. Sean $\mathcal{C}_1$ y $\mathcal{C}_2$ circunferencias no concéntricas de centros $O_1$ y $O_2$. Si $P$ es un punto equipotente con respecto a ellas y $M$ es el pie de la perpendicular desde $P$ a la recta $O_1O_2$, entonces $M$ es equipotente con respecto a las dos circunferencias.

Demostración. Sean $r_1$ y $r_2$ los radios de $\mathcal{C}_1$ y $\mathcal{C}_2$, respectivamente. Como $P$ esta en el eje radical de ambas, entonces por cómo se calcula la potencia con la distancia a los centros y el radio, tenemos que

\begin{equation}\label{eq:pot-ambos}PO_1^2 – r_1^2 = PO_2^2 – r_2^2.\end{equation}

Queremos demostrar que $M$ pertenece al eje radical, osea $\text{Pot}(M,\mathcal{C}_1)=\text{Pot}(M,\mathcal{C}_2)$.

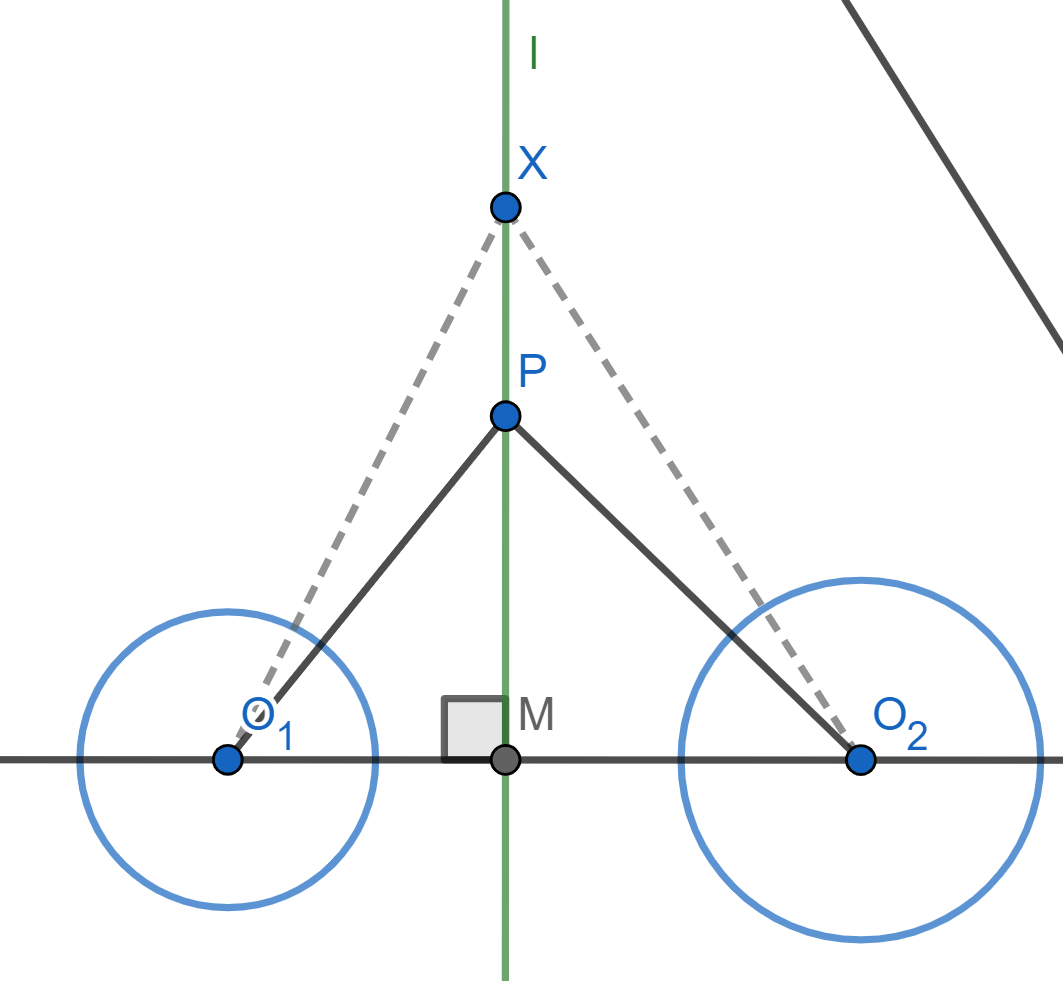
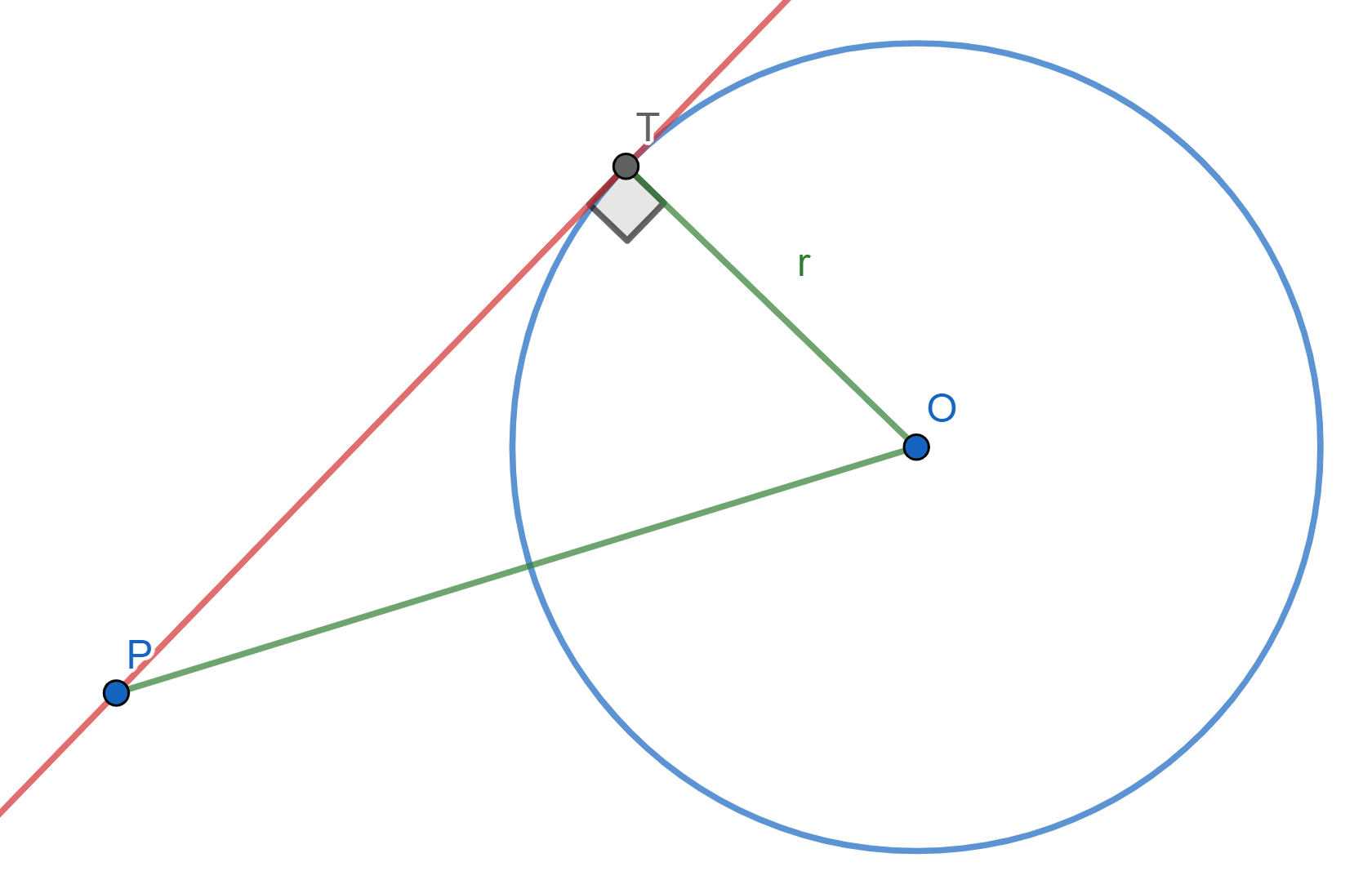
Tracemos los segmentos $O_1P$ y $O_2P$. Los triángulos $\triangle PMO_1$ y $\triangle PMO_2$ son rectángulos, ver la siguiente figura.

Por Pitágoras se sigue que $$PO_1^2=MO_1^2+PM^2$$ y $$PO_2^2=MO_2^2+PM^2.$$

Al sustituir en \eqref{eq:pot-ambos}, obtenemos: $$MO_1^2+PM^2-r_1^2=MO_2^2+PM^2-r_2^2.$$

Cancelando $PM^2$, se obtiene la expresión que muestra que $M$ también es equipotente a ambas circunferencias:

\begin{equation}\label{eq:Mradical}MO_1^2-r_1^2=MO_2^2-r_2^2.\end{equation}

$\square$

Ahora veremos que todos los puntos en la perpendicular por $M$ también son equipotentes.

Proposición. Sean $\mathcal{C}_1$ y $\mathcal{C}_2$ circunferencias no concéntricas de centros $O_1$ y $O_2$. Si $M$ es un punto en $O_1O_2$ equipotente a ambas circunferencias, entonces todos los puntos en la perpendicular a $O_1O_2$ por $M$ también lo son.

Demostración. A la perpendicular del enunciado la llamaremos $l$. Sea $X$ un punto en $l$. Debemos mostrar que $$\text{Pot}(X,\mathcal{C}_1)=\text{Pot}(X,\mathcal{C}_2).$$

Para ello, trazamos $O_1X$ y $O_2X$.

Eje radical de 2 circunferencias demostración de proposición.

Como los triángulos $\triangle XMO_1$ y $\triangle XMO_2$ son rectángulos, nuevamente por Pitágoras: $$XO_1^2=MO_1^2+XM^2$$ y $$XO_2^2=MO_2^2+XM^2.$$

Usando las igualdades anteriores y que $M$ está en el eje radical (específicamente, \eqref{eq:Mradical}), tenemos que:

\begin{align*}
\text{Pot}(X,\mathcal{C}_1)&=XO_1^2-r_1^2\\
&= MO_1^2+XM^2 – r_1^2\\
&=MO_2^2+XM^2 – r_2^2\\
&=XO_2^2-r_2^2\\
&=\text{Pot}(X,\mathcal{C}_2).
\end{align*}

Por lo tanto, todo punto $X$ en $l$ es un punto en el eje radical.

$\square$

Ya sólo nos falta ver que no hay más puntos equipotentes.

Proposición. Sean $\mathcal{C}_1$ y $\mathcal{C}_2$ circunferencias no concéntricas de de centros $O_1$ y $O_2$. Si $M$ es un punto en $O_1O_2$ equipotente a ambas circunferencias, entonces únicamente los puntos en la perpendicular a $O_1O_2$ por $M$ son equipotentes a las circunferencias.

Demostración. Primero veremos que el único punto en $O_1O_2$ que puede funcionar es $M$. Para buscar una contradicción supongamos que otro punto $N$ en la recta $O_1O_2$, con $N\neq M$ también cumple que $\text{Pot}(N,\mathcal{C}_1)=\text{Pot}(N,\mathcal{C}_2)$. Entonces, $$NO_1^2-r_1^2=NO_2^2-r_2^2.$$

Restando a esta ecuación la ecuación \eqref{eq:Mradical}, obtenemos que $$NO_1^2-MO_1^2 = NO_2^2-MO_2^2,$$ y por diferencia de cuadrados, $$(NO_1+MO_1)(NO_1-MO_1)=(NO_2+MO_2)(NO_2-MO_2).$$

Tenemos que $NO_1-MO_1=NO_1+O_1M=NM$ y lo análogo para $O_2$, de modo que $$(NO_1+MO_1)NM=(NO_2+MO_2)NM.$$

Como $N\neq M$, tenemos $NM\neq 0$ y lo podemos cancelar. $$NO_1+MO_1=NO_2+MO_2,$$

de donde sale la cuarta igualdad de la siguiente cadena:

\begin{align*}
O_2O_1&=O_2N+NO_1\\
&=-NO_2+NO_1\\
&=-MO_1+MO_2\\
&=O_1M+MO_2\\
&=O_1O_2.
\end{align*}

Obtenemos que $O_2O_1=O_1O_2$. ¡Esto es imposible, pues son segmentos dirigidos y $O_1\neq O_2$! Esta contradicción muesta que $M$ es el único punto en $O_1O_2$ equipotente a ambas circunferencias.

Para finalizar, supongamos que existe un punto $P’$ cualquiera del plano equipotente a $\mathcal{C}_1$ y $\mathcal{C}_2$. Por la proposición de la proyección, la proyección $M’$ de $P’$ en $O_1O_2$ también es equipotente. Por lo que acabamos de mostrar, $M=M’$. Y así, $P’$ está en la perpendicular a $O_1O_2$ por $M$, como queríamos.

$\square$

Los ejes radicales por parejas de 3 circunferencias son concurrentes

Si tenemos tres circunferencias, entonces definen tres ejes radicales. Estos tres ejes radicales siempre concurren.

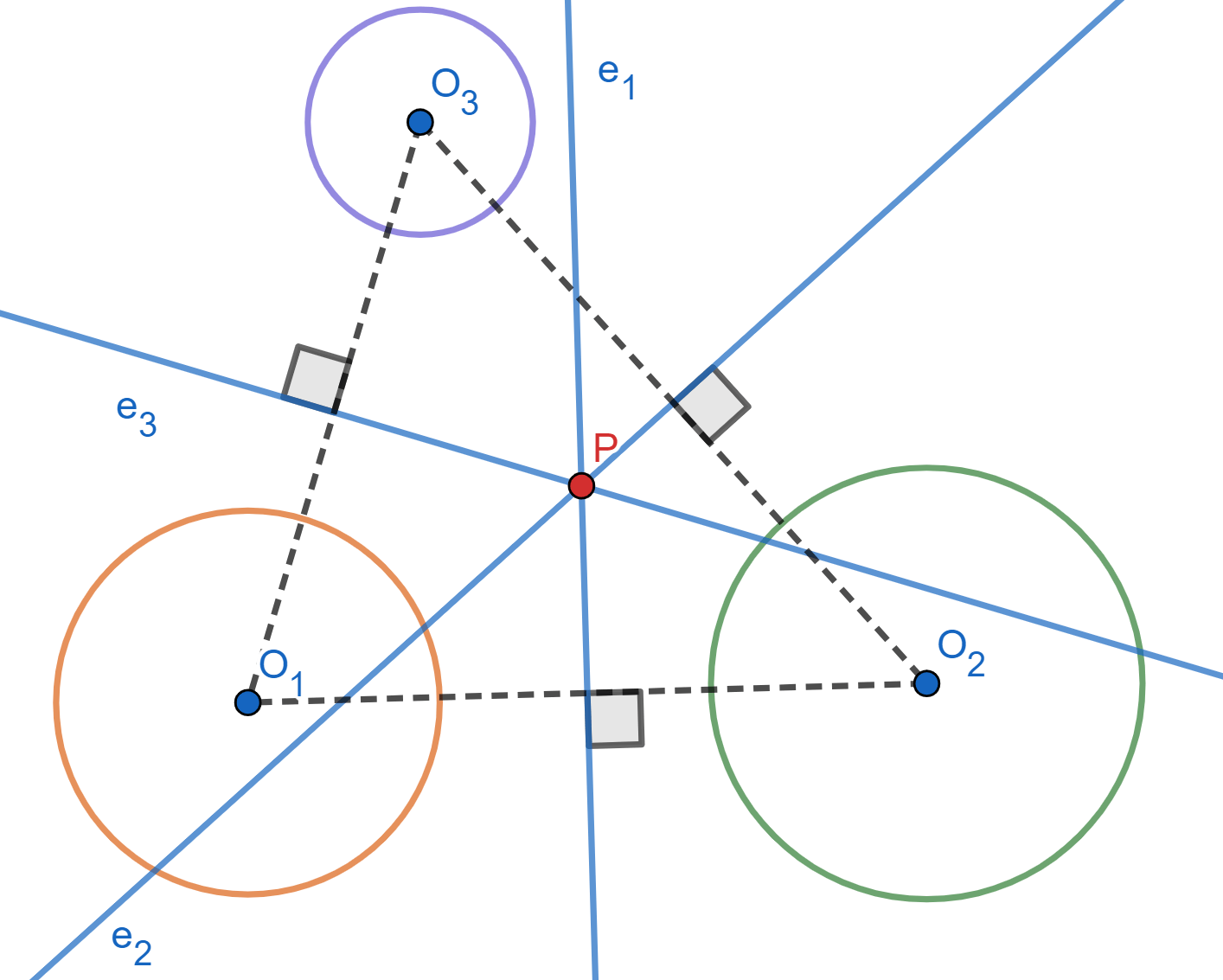
Teorema. Sean $\mathcal{C}_1$, $\mathcal{C}_2$ y $\mathcal{C}_3$ circunferencias de centros no colineales. Sea $e_1$ el eje radical de $\mathcal{C}_1$ y $\mathcal{C}_2$. Sea $e_2$ el eje radical de $\mathcal{C}_2$ y $\mathcal{C}_3$. Sea $e_3$ el eje radical de $\mathcal{C}_3$ y $\mathcal{C}_1$. Las rectas $e_1,e_2,e_3$ son concurrentes.

Demostración. Consideremos 3 circunferencias $\mathcal{C}_1,\mathcal{C}_2$ y $\mathcal{C}_3$, cuyos centros $O_1$, $O_2$ y $O_3$ no son colineales (en particular, son distintos). Tomemos los ejes radicales $e_1,e_2,e_3$ como en el enunciado.

Llamamos $P$ al punto de intersección de $e_1$ y $e_2$. Como $P$ está en $e_1$, entonces $\text{Pot}(P,\mathcal{C}_1)=\text{Pot}(P,\mathcal{C}_2)$ y como $P$ está en $e_2$, entonces $\text{Pot}(P,\mathcal{C}_2)=\text{Pot}(P,\mathcal{C}_3)$. De esta manera, $$\text{Pot}(P,\mathcal{C}_1)=\text{Pot}(P,\mathcal{C}_3).$$ Esto muestra que también $P$ está en $e_3$. Por lo tanto, los 3 ejes radicales concurren en $P$.

$\square$

Construcción del eje radical

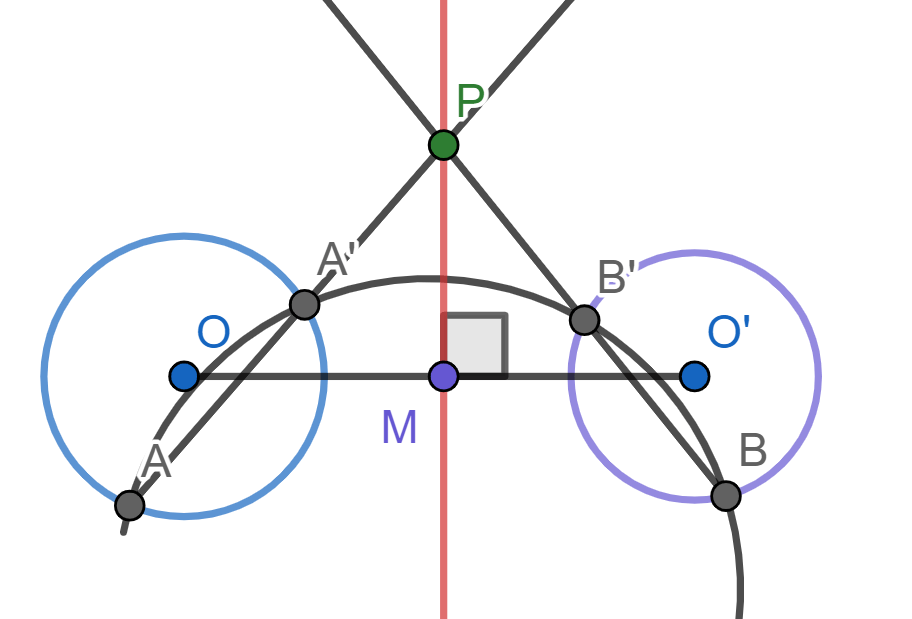
¿Cómo podemos dibujar el eje radical de dos circunferencias no concéntricas $\mathcal{C}_1$ y $\mathcal{C}_2$, digamos, con regla y compás? Podemos seguir la idea que usamos cuando probamos que por lo menos existe un punto en el eje radical. Sean $O_1$ y $O_2$ los centros de estas circunferencias, respectivamente.

Dibujemos una circunferencia $\mathcal{C}$ que corte a las circunferencias $\mathcal{C}_1$ y $\mathcal{C}_2$, en $A,A’$ y $B,B’$. Esto puede hacerse trazando el circuncírculo de $O_1$, $O_2$ y un punto fuera de ambas cirfunferencias. Sean $A$ y $A’$ las intersecciones de $\mathcal{C}$ con $\mathcal{C}_1$. Sean $B$ y $B’$ las intersecciones de $\mathcal{C}$ con $\mathcal{C}_2$. Tomemos $P$ la intersección de $AA’$ y $BB’$. Por lo que mostramos anteriormente, $P$ está en el eje radical de las circunferencias. Y además, también mostramos que la recta perpendicular a $O_1O_2$ por $P$ es el eje radical. Así, al trazar esta perpendicular, obtenemos el eje radical requerido.

Más adelante…

Se seguirá abordando el tema de potencia de un punto y el eje radical con respecto a las circunferencias ortogonales.

Al final de los temas de esta primera unidad se dejará una serie de ejercicios.

Entradas relacionadas

Geometría Moderna II: Potencia de un punto

Por Armando Arzola Pérez

Deja un comentario

Introducción

En esta primera unidad abordaremos varios los temas relacionados con las circunferencias coaxiales. Para ello, iniciaremos hablando de la potencia de un punto con respecto a una circunferencia. A grandes rasgos, esto trata de lo siguiente.

Tomemos una circunferencia $\mathcal{C}$. Tomemos $P$ un punto cualquiera. Tomemos una recta $l$ por $P$ y llamemos $A$ y $B$ los puntos de intersección de $l$ con $\mathcal{C}$. Bajo estas elecciones, la potencia de $P$ será $PA\cdot PB$. Lo que veremos en esta entrada es que dicho producto es constante sin importar la elección de $l$. Para mostrar esto, introduciremos algunas definiciones y posteriormente haremos una demostración por casos.

Definición de potencia de un punto

Comenzaremos dando una primer definición de potencia, que dependerá de cierto punto, circunferencia y recta que elijamos.

Definición. Sea $\mathcal{C}$ una circunferencia, $P$ un punto y $l$ una recta que intersecta a $\mathcal{C}$. Sean $A$ y $B$ los puntos de intersección de $l$ y $\mathcal{C}$ ($A=B$ si $l$ es tangente a $\mathcal{C}$). La potencia de $P$ con respecto a $\mathcal{C}$ en la recta $l$ es la cantidad $PA\cdot PB$. Usaremos la siguiente notación: $$\text{Pot}(P,\mathcal{C},l):=PA\cdot PB.$$

En esta definición y de aquí en adelante, a menos que se diga lo contrario, se estará trabajando con segmentos dirigidos. Es decir, estamos pensando que cada segmento tiene una dirección del primer punto al segundo. Así, por ejemplo, el valor de $PA$ dependerá de la longitud del segmento y su signo dependerá de una dirección (usualmente implícita) que se le asigne a la recta por $A$ y $P$. De este modo, tendremos, por ejemplo, que $PA=-AP$.

La definición de potencia de un punto puede simplificarse notablemente en vista de la siguiente proposición.

Proposición. La potencia de un punto con respecto a una circunferencia no depende de la recta elegida. Es decir, tomemos $\mathcal{C}$ una circunferencia, $P$ un punto y $l,m$ rectas. Supongamos que los puntos de intersección de $l$ con $\mathcal{C}$ son $A$ y $B$; y que los puntos de intersección de $m$ con $\mathcal{C}$ son $C$ y $D$ (en caso de tangencias, repetimos los puntos). Entonces: $$PA\cdot PB = PC\cdot PD.$$

Demostración. Haremos la demostración por casos de acuerdo a cuando $P$ está dentro o fuera de la circunferencia, o sobre ella.

Dentro de la circunferencia:

Tomemos las cuerdas $AB$ y $CD$ en la circunferencia, las cuales se cortan en $P$. Los triángulos $\triangle APC$ y $\triangle DPB$ son semejantes ya que:

Geometría Moderna II: Potencia de un punto proposición 1 cuando el punto está dentro de la circunferencia.
  1. $\angle PAC = \angle PDB $ por abrir el mismo arco $\overline{BC}$.
  2. $\angle APC = \angle BPD $ por ser opuestos al vértice.
  3. $\angle PCA = \angle PBD $ por abrir mismo arco $\overline{AD}$.

Entonces de la semejanza $\triangle APC \cong \triangle DPB $ tenemos que

$\frac{PA}{PD}=\frac{PC}{PB},$

de donde obtenemos la igualdad $PA\cdot PB =PC \cdot PD$ deseada.

Fuera de la circunferencia:

Ahora, $AB$ y $CD$ son dos secantes que se intersecan en $P$, pero con $P$ exterior a $\mathcal{C}$. Tenemos que $\triangle APC $ y $\triangle DPB $ son semejantes, ya que:

Geometría Moderna II: Potencia de un punto proposición 1 cuando el punto está fuera de la circunferencia.
  1. El cuadrilátero $\square ABDC$ es cíclico, entonces: $\angle ACD + \angle ABD = 180^\circ$ y $\angle ABD + \angle DBP = 180^\circ $, de donde $\angle DBP = \angle ACD$.
  2. $\angle BPD$ y $\angle CPA$ son los mismos ángulos.

Entonces $\frac{PA}{PC}=\frac{PD}{PB},$ de donde se obtiene la igualdad buscada $PA\cdot PB=PC\cdot PD.$

Sobre la circunferencia:

Este caso es sencillo pues sin importar las secantes tomadas, en cada una hay un punto igual a $P$ y por lo tanto una distancia igual a cero. De este modo, $PA\cdot PB=0=PC\cdot PD$.

$\square$

Nota que las demostraciones anteriores sirven aunque $l$ ó $m$ sean tangentes, sólo que hay que hacer ligeras adaptaciones sobre los ángulos usados y los motivos por los que son iguales. Enunciaremos el caso de la tangencia un poco más abajo.

En vista de la proposición anterior, podemos simplificar nuestra definición notablemente.

Definición. Sea $\mathcal{C}$ una circunferencia y $P$ un punto. Tomemos $l$ una recta que intersecta a $\mathcal{C}$. Sean $A$ y $B$ los puntos de intersección de $l$ y $\mathcal{C}$ ($A=B$ si $l$ es tangente a $\mathcal{C}$). La potencia de $P$ con respecto a $\mathcal{C}$ es la cantidad $PA\cdot PB$. Usaremos la siguiente notación: $$\text{Pot}(P,\mathcal{C}):=PA\cdot PB.$$

La potencia queda bien definida sin importar la recta $l$, debido a la proposición anterior.

El signo de la potencia

En esta definición estamos usando segmentos dirigidos, y eso nos lleva a que la potencia de un punto puede tener distintos signos. El comportamiento queda determinado por el siguiente resultado.

Proposición. La potencia de un punto $P$ con respecto a una circunferencia $\mathcal{C}$ es positiva, negativa o cero, de acuerdo a si el punto $P$ está fuera de $\mathcal{C}$, dentro de ella, o sobre ella, respectivamente.

Demostración. Veamos esto caso por caso.

  • Sea $P$ un punto externo a $\mathcal{C}$. Entonces $PA$ y $PB$ tienen la misma orientación y por lo tanto el mismo signo. Además, como $P$ no está sobre $\mathcal{C}$, ninguno de ellos es cero. Así, $\text{Pot}(P,\mathcal{C})> 0$.
Geometría Moderna II: Potencia de un punto respecto a un punto externo.
  • Sea $P$ un punto interno a $\mathcal{C}$. Entonces $PA$ está dirigido hacia un lado y $PB$ está dirigido hacia el otro, de modo que tienen signo contrario. Además, ninguno de ellos es cero. Así, $\text{Pot}(P,\mathcal{C})<0$.
Geometría Moderna II: Potencia de un punto respecto a un punto interno de la circunferencia.
  • Finalmente, sea $P$ un punto sobre $\mathcal{C}$. Esto quiere decir que alguno de los puntos $A$ o $B$ es $P$ (quizás ambos, si $l$ es tangente). Así, $PA=0$ ó $PB=0$. De este modo $\text{Pot}(P,\mathcal{C})=0$.
Geometría Moderna II: Potencia de un punto que está sobre la circunferencia.

$\square$

Otras fórmulas para la potencia

La potencia es invariante sin importar la recta elegida. De este modo, podemos elegir a una recta tangente y obtener una fórmula para la potencia en términos de la longitud de dicha tangente.

Proposición. Sea $\mathcal{C}$ una circunferencia. Para un punto $P$ fuera de $\mathcal{C}$, su potencia es igual al cuadrado de la longitud de una tangente de él a la circunferencia.

Es decir, sea $T$ un punto sobre la circunferencia tal que $PT$ sea tangente a $\mathcal{C}$. Entonces, $\text{Pot}(P,\mathcal{C})=PT^2$.

Imagen representativa de la Proposición 2.

El resultado se sigue de llevar al límite lo que ya probamos en la proposición de invarianza de la potencia. Pero a continuación damos un argumento alternativo.

Demostración. Tracemos otra recta por $P$ que no sea tangente a $\mathcal{C}$ y cuyos puntos de intersección con $\mathcal{C}$ son $A$ y $B$ como en la figura. Tenemos que mostrar que $PA\cdot PB =PT^2$.

El ángulo $\angle PTA$ es semi-inscrito y es igual al ángulo inscrito $ \angle TBA$, pues ambos tienen el mismo arco $\overline{AT}$.

Entonces los triángulos $\triangle APT$ y $\triangle TPB$ comparten el ángulo con vértice en $P$ y $\angle PTA=\angle TBA$. Por ello, se tiene que $\triangle APT \cong \triangle TPB $ son semejantes y sus lados son proporcionales: $\frac{PA}{PT} = \frac{PT}{PB}$. De aquí, $$PT^2=PT\cdot PT=PA\cdot PB=\text{Pot}(P,\mathcal{C}).$$

$\square$

También es posible conocer la potencia de un punto hacia una circunferencia si conocemos el radio de la circunferencia y la distancia del punto al centro.

Proposición. Sea $\mathcal{C}$ una circunferencia de centro $O$ y radio $r$. Sea $P$ un punto en cualquier posición. La potencia de $P$ con respecto a $\mathcal{C}$ es $$\text{Pot}(P,\mathcal{C}) = OP^2 – r^2.$$

Demostración. Haremos la demostración por casos

Dentro de la circunferencia:

Sea $AB$ la cuerda que pasa por el centro $O$ y $P$ (si $O=P$, tomamos cualquier cuerda $AB$ por el centro). Supongamos sin pérdida de generalidad que la recta está dirigida de $A$ a $B$. Tenemos que $AO=r>0$ y llamemos $d=OP>0$. De aquí, $PB=r-d>0$. La siguiente figura resume estas igualdades.

Potencia de un punto imagen de Proposición 3 cuando un punto está dentro de la circunferencia.

La potencia desde $P$ sería entonces, cuidando los signos:

\begin{align*}
PA\cdot PB &= (PO+OA)(PB)\\
&=(-d-r)(r-d)\\
&=-(d+r)(r-d)\\
&=-(r^2-d^2)\\
&=d^2-r^2\\
&=OP^2-r^2.
\end{align*}

Así, $\text{Pot}(P,\mathcal{C})=OP^2-r^2$.

Fuera de la circunferencia:

Ahora desde $P$ tracemos una tangente $PT$ a $\mathcal{C}$ con $T$ sobre $\mathcal{C}$. Como $\angle PTO =90^o$, entonces $\triangle POT$ es un triángulo rectángulo.

Potencia de un punto imagen de Proposición 3 cuando un punto está fuera de la circunferencia.

Por el teorema de Pitágoras y la expresión de potencia en términos de la tangente: $$OP^2=r^2+PT^2=r^2+\text{Pot}(P,\mathcal{C}).$$ Despejando, obtenemos la expresión deseada: $$\text{Pot}(P,\mathcal{C})=OP^2-r^2.$$

Sobre la circunferencia:

Este caso es sencillo, pues sabemos que la potencia de $P$ debe ser cero. Pero además, como $P$ está en la circunferencia, entonces $OP=r$, de modo que $OP^2-r^2=0$, y entonces la expresión también es lo que queremos.

$\square$

Más adelante…

Seguiremos abordando el tema de potencia de un punto y veremos cómo a partir de él se define el eje radical de dos circunferencias.

Entradas relacionadas