Introducción
En entradas anteriores definimos la razón en la que un punto divide a un segmento e hicimos uso de este concepto, obviando el cambio de signo, nos podemos preguntar que es lo que pasa cuando dos puntos distintos dividen en la misma razón a un segmento, esto es lo que se conoce como división armónica.
Definición 1. Definimos la razón cruzada de dos pares de puntos colineales $(A, B)$ y $(C, D)$ como
$(A, B; C, D) = \dfrac{AC}{CB} \div \dfrac{AD}{DB}$.
Si $C$ está en el segmento $AB$, $D$ en su extensión y la razón en la que $C$ y $D$ dividen al segmento $AB$ es la misma en valor absoluto, entonces $(A, B; C, D) = – 1$.
En este caso, decimos que $C$ y $D$ dividen al segmento $AB$ armónicamente, o que $C$ y $D$ son conjugados armónicos respecto de $A$ y $B$.
Observación. Notemos que el conjugado armónico de un punto respecto de otros dos puntos dados es único, pues ya probamos que para todo número real $r$, existe un único punto que divide a un segmento dado en $r$.
Hilera armónica
Teorema 1. Si dos puntos $C$ y $D$ dividen armónicamente al segmento $AB$ en la razón $|\dfrac{p}{q}|$ entonces los puntos $A$ y $B$ dividen armónicamente a $CD$ en la razón $|\dfrac{p – q}{p + q}|$.
Demostración. Supongamos que $\dfrac{AC}{CB} = \dfrac{p}{q}$ y $\dfrac{AD}{DB} = \dfrac{– p}{q}$, entonces usando segmentos dirigidos,
$\dfrac{AC}{CB} + \dfrac{CB}{CB} = \dfrac{p}{q} + \dfrac{q}{q} \Rightarrow$
$\begin{equation} \dfrac{AB}{CB} = \dfrac{p + q}{q}. \end{equation}$
$\dfrac{AD}{DB} + \dfrac{DB}{DB} = \dfrac{– p}{q} + \dfrac{q}{q} \Rightarrow$
$\begin{equation} \dfrac{AB}{DB} = \dfrac{q – p}{q}. \end{equation}$
De manera análoga podemos encontrar
$\begin{equation} \dfrac{AB}{AC} = \dfrac{CB + AC}{AC} = \dfrac{q + p}{p}, \end{equation}$
$\begin{equation} \dfrac{AB}{AD} = \dfrac{DB + AD}{AD} = \dfrac{p – q}{p}. \end{equation}$
Haciendo el cociente de $(2)$ entre $(1)$ obtenemos
$\dfrac{CB}{BD} = \dfrac{p – q}{p + q}$.
Análogamente de $(4)$ y $(3)$ obtenemos
$\dfrac{CA}{AD} = \dfrac{q – p}{p + q}$.
$\blacksquare$
Definición 2. Debido a esta propiedad reciproca en la que si $(A, B; C, D) = – 1$ entonces $(C, D; A, B) = – 1$, decimos que $ACBD$ es una hilera armónica de puntos o simplemente una hilera armónica.
Corolario 1. Si $(A, B; C, D) = – 1$, entonces $\dfrac{AB}{CD} = \dfrac{p^2 – q^2}{2pq}$.
Demostración. $CD = AD – AC $
$= ABp(\dfrac{1}{p – q} – \dfrac{1}{p + q}) = ABp(\dfrac{p + q – (p – q)}{p^2 – q^2})$.
Donde la segunda igualdad se debe a $(3)$ y $(4)$.
Por lo tanto, $\dfrac{AB}{CD} = \dfrac{p^2 – q^2}{2pq}$.
$\blacksquare$
Construcción del conjugado armónico
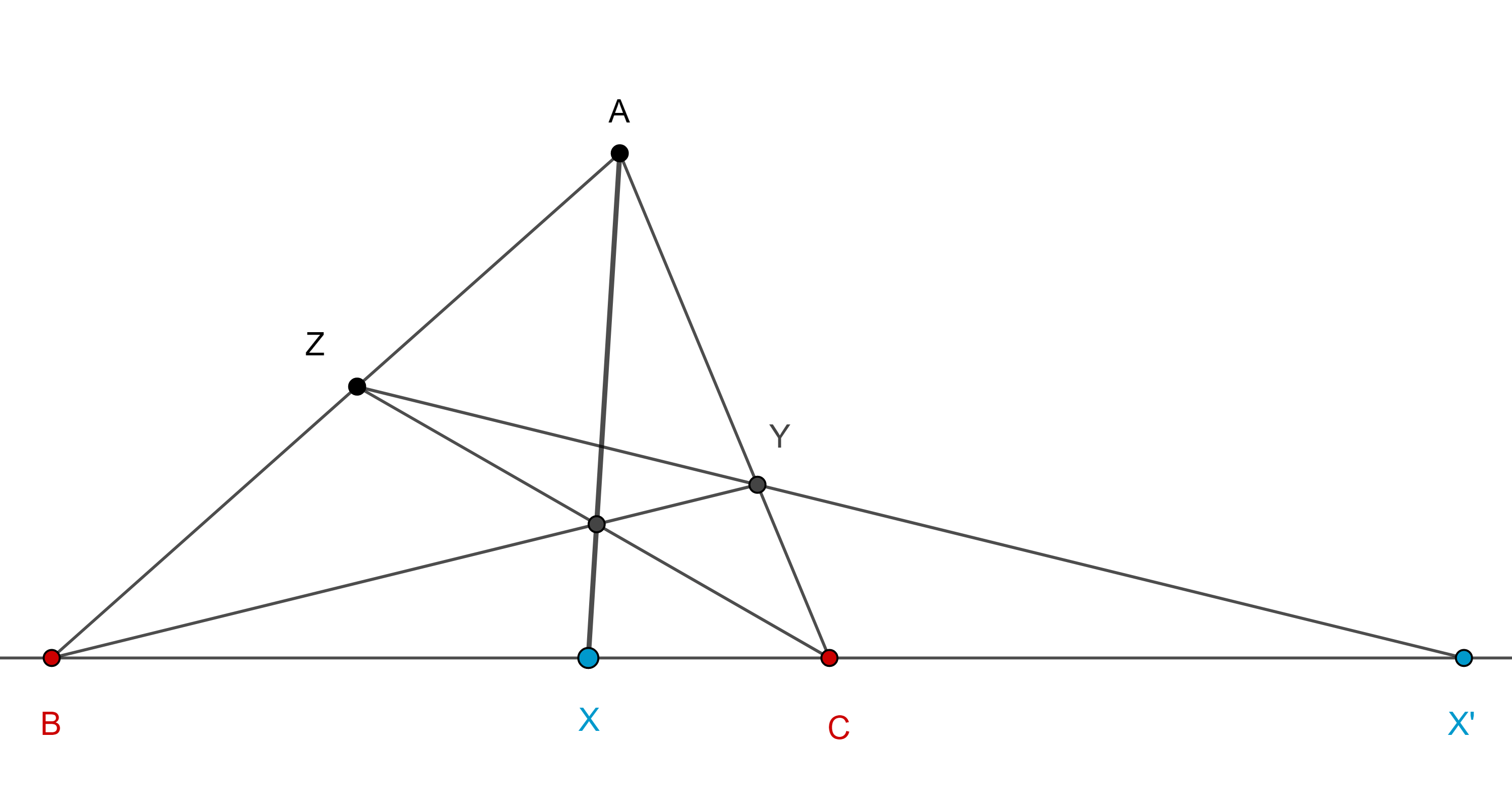
Teorema 2. Sea $\triangle ABC$, considera $X \in BC$, $Y \in CA$, $Z \in AB$, cada uno en el interior del lado respectivo y sea $X’ = ZY \cap BC$, entonces $X$ y $X’$ son conjugados armónicos respecto a $BC$ si y solo si $AX$, $BY$, $CZ$ son concurrentes.
Demostración. Aplicando el teorema de Menelao a $\triangle ABC$ y la transversal $X’YZ$ tenemos
$\dfrac{AZ}{ZB} \dfrac{BX’}{X’C} \dfrac{CY}{YA} = – 1$.
Por el teorema de Ceva $AX$, $BY$, $CZ$ son concurrentes si y solo si,
$\dfrac{AZ}{ZB} \dfrac{BX}{XC} \dfrac{CY}{YA} = 1$.
Dividiendo ambas expresiones obtenemos
$(B, C; X, X’) = \dfrac{BX}{XC} \div \dfrac{BX’}{X’C} = – 1$.
$\blacksquare$
Proposición 1. Las proyecciones de los puntos de una hilera armónica en cualquier recta, forman otra hilera armónica.
Demostración. Sean $ACBD$ una hilera armónica y $l$ cualquier otra recta, consideremos $A’$, $B’$, $C’$, $D’$, las proyecciones de $A$, $B$, $C$, $D$ respectivamente en $l$.
Sea $P = ACBD \cap l$, como $AA’ \parallel BB’ \parallel DD’$, tenemos las siguientes semejanzas, $\triangle PB’B \sim \triangle PD’D \sim \triangle PA’A$ (figura 3), es decir:
$\dfrac{PA’}{PD’} = \dfrac{PA}{PD} \Leftrightarrow \dfrac{– A’P – PD’}{PD’} = \dfrac{– AP – PD}{PD}$
$\Leftrightarrow \dfrac{A’D’}{AD} = \dfrac{P’D’}{PD}$.
Igualmente podemos ver que $\dfrac{D’B’}{DB} = \dfrac{P’D’}{PD}$.
Por lo tanto $\dfrac{A’D’}{D’B’} = \dfrac{AD}{BD}$.
De manera análoga podemos encontrar $\dfrac{A’C’}{C’B’} = \dfrac{AC}{CB}$.
Como $(A, B; C, D) = – 1$, entonces,
$\dfrac{A’D’}{D’B’} = \dfrac{AD}{BD} = – \dfrac{AC}{CB} = – \dfrac{A’C’}{C’B’}$.
$\blacksquare$
División armónica y bisectrices
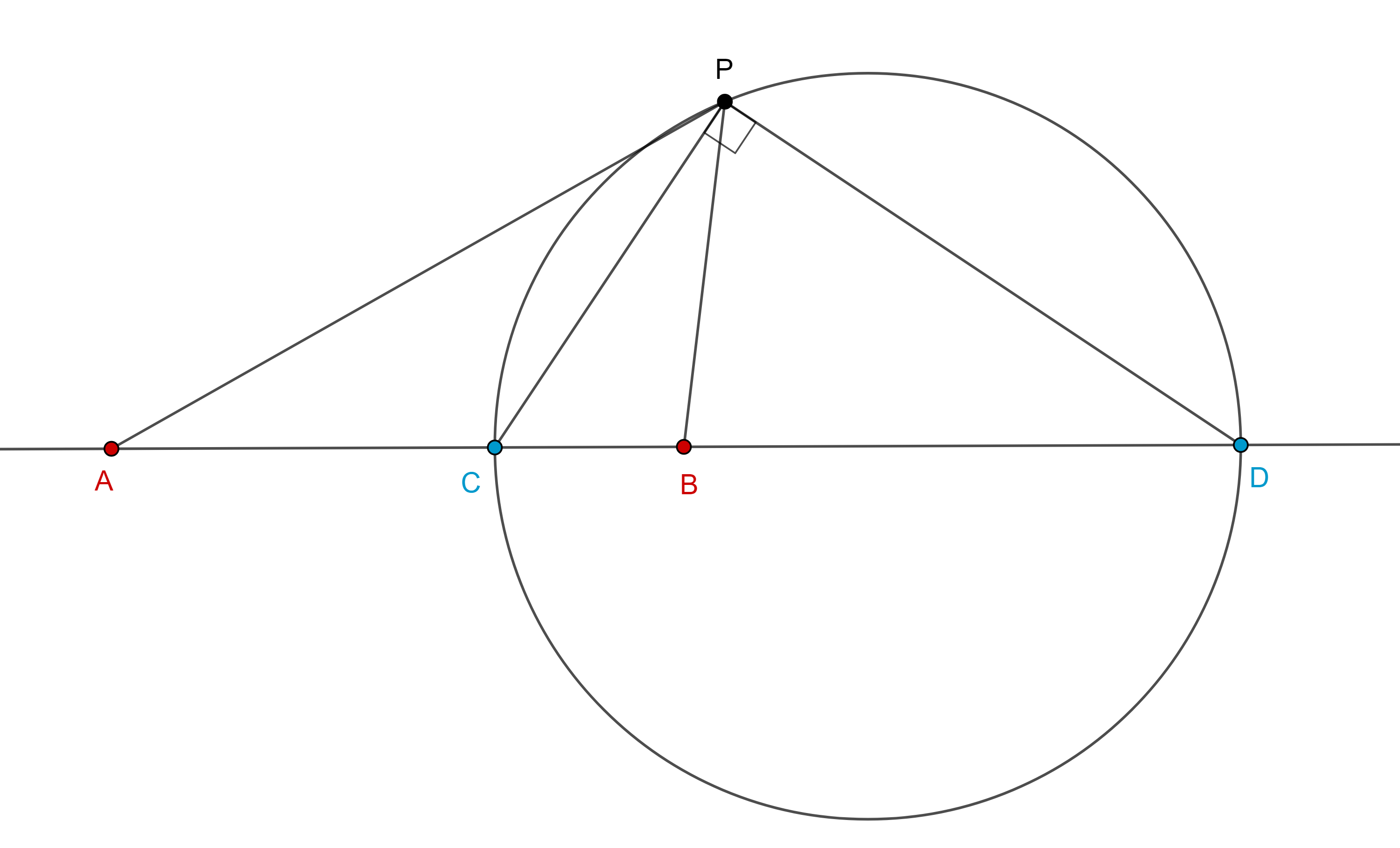
Teorema 3. Sean $A$, $C$, $B$, $D$, cuatro puntos colineales, en ese orden, sea $P$ un punto fuera de la recta $ACBD$, entonces, si dos de las siguientes tres propiedades son ciertas, la tercera también es cierta:
$i)$ $(A, B; C, D) = – 1$,
$ii)$ $PC$ es la bisectriz interna de $\angle APB$,
$iii)$ $PC \perp PD$.
Demostración.
$i)$ y $ii)$ se cumplen, como $PC$ es la bisectriz interna de $\angle APB$, por el teorema de la bisectriz, la bisectriz externa de $\angle APB$ interseca a $AB$ en el conjugado armónico de $C$, el cual es único por la observación hecha en la introducción.
Por lo tanto, $PD$ es la bisectriz externa de $\angle APB$ y así $PC \perp PD$.
$ii)$ y $iii)$ se cumplen, ya que $PC$ es la bisectriz interna de $\angle APB$ y $PC \perp PD$, entonces $PD$ es la bisectriz externa de $\angle APB$.
Por el teorema de la bisectriz, $C$ y $D$ son conjugados armónicos.
$i)$ y $iii)$ se cumplen, si $C$ y $D$ son conjugados armónicos respecto de $AB$ entonces se encuentran en la circunferencia de Apolonio determinada por la razón $\dfrac{AC}{CB} =|\dfrac{AD}{DB}|$.
Recordemos que $CD$ es diámetro de esta circunferencia, como $PC \perp PD$, entonces $P$ pertenece a este lugar geométrico.
Por lo tanto, $\dfrac{AP}{PB} = \dfrac{AC}{CB} =|\dfrac{AD}{DB}|$, por el reciproco del teorema de la bisectriz, $PC$ y $PD$ son las bisectrices interna y externa de $\angle APB$ respectivamente.
$\blacksquare$
Corolario 2. Considera un triángulo $\triangle ABC$, $I$ el incentro, $I_c$ el excentro relativo al vértice $C$ y $C_1 = CI \cap AB$, entonces $(C, C_1; I, I_c) = -1$.
Demostración. En $\triangle AC_1C$, $AI$ y $AI_c$ son las bisectrices interna y externa respectivamente de $\angle C_1AC$.
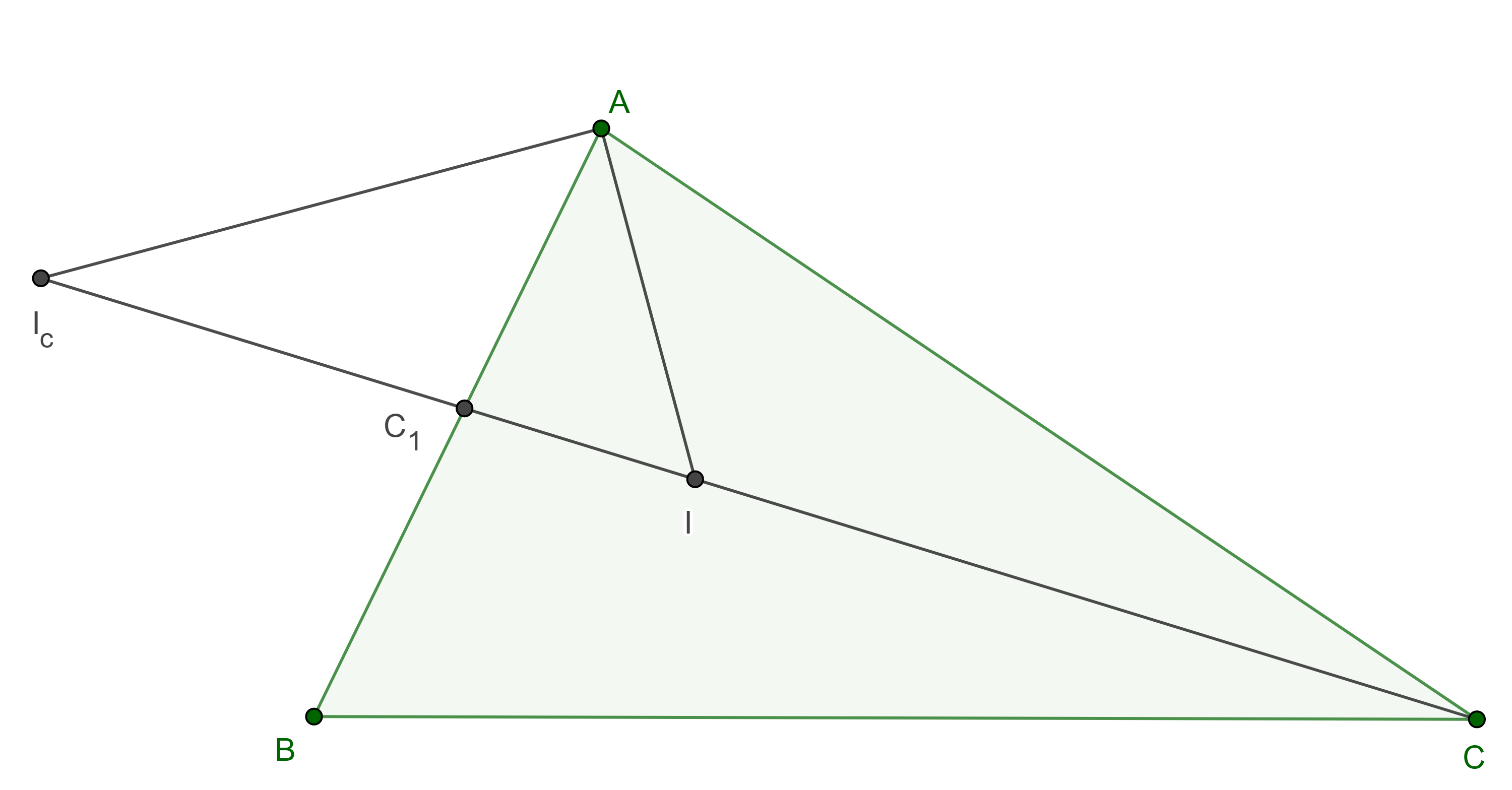
Como se cumplen los puntos $ii)$ y $iii)$ del teorema anterior entonces $(C, C_1; I, I_c) = -1$.
$\blacksquare$
Punto medio de conjugados armónicos
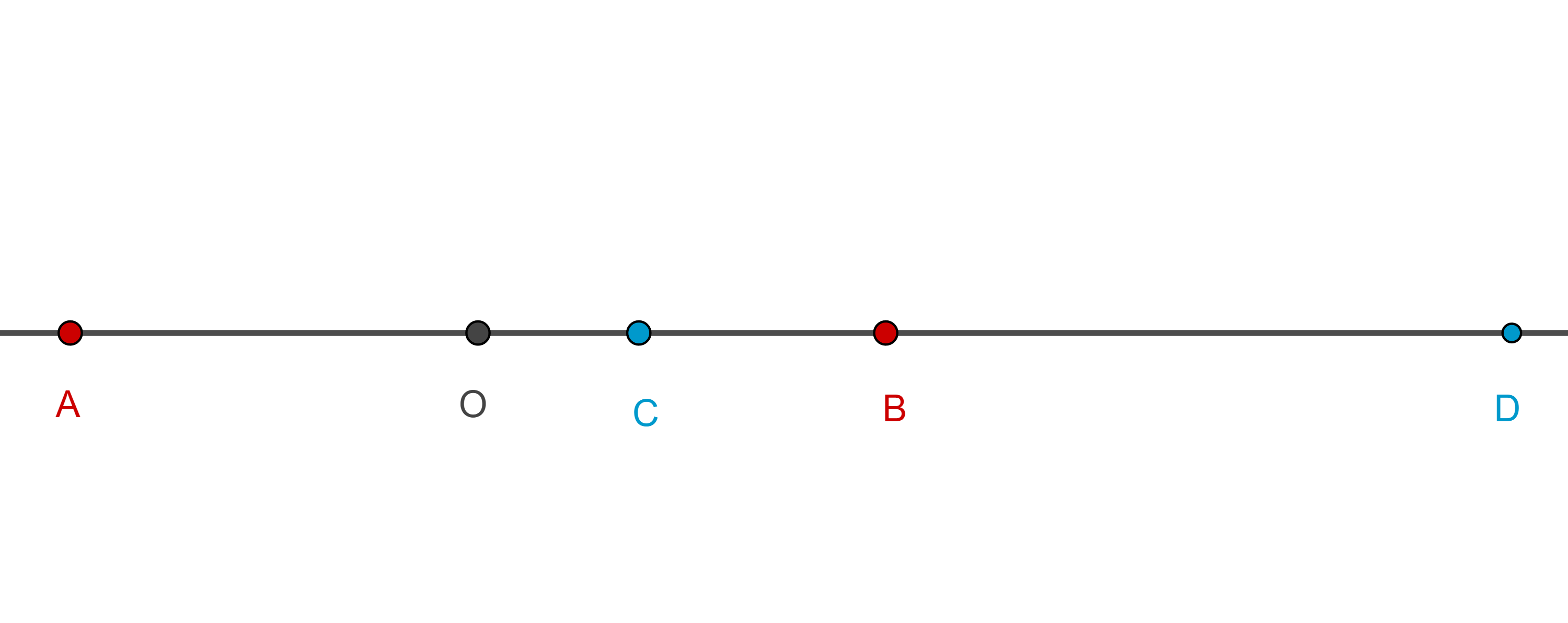
Teorema 4. Si $A$, $C$, $B$, $D$, son cuatro puntos colineales, en ese orden, y $O$ el punto medio del segmento $AB$ entonces $(A, B; C, D) = – 1$ si y solo si $OC \times OD = OA^2$.
Demostración. Empleando segmentos dirigidos tenemos lo siguiente:
$AC – CB = (AO + OC) – (CO + OB) = 2OC$,
$AD – DB = (AO + OD) – (DO + OB) = 2OD$,
$AC + CB = AB = AD + DB = 2AO$.
Por lo tanto, $OC \times OD = OA^2$
$\Leftrightarrow 2OC \times 2OD = (2AO)^2$
$\Leftrightarrow (AC – CB)( AD – DB) = (AC + CB)(AD + DB)$
$ \Leftrightarrow (AC \times AD) – (AC \times DB) – (AD \times CB) + (CB \times DB)$
$= (AC \times AD) + (AC \times DB) + (AD \times CB) + (CB \times DB)$
$\Leftrightarrow – 2AC \times DB = 2AD \times CB$
$\Leftrightarrow (A, B; C, D) = – 1$.
$\blacksquare$
Proposición 2.Sean $A$, $C$, $B$, $D$, cuatro puntos colineales, entonces $(A, B; C, D) = – 1$, si y solo si al medir todos los segmentos de un punto de la hilera armónica, $B$ por ejemplo, tenemos $\dfrac{2}{BA} = \dfrac{1}{BC} + \dfrac{1}{BD}$.
Demostración. $\dfrac{AC}{CB} = – \dfrac{AD}{DB}$
$ \Leftrightarrow \dfrac{AB + BC}{CB} = – \dfrac{AB + BD}{DB}$
$\Leftrightarrow \dfrac{BA}{BC} – 1 = \dfrac{BA}{DB} + 1$
$\Leftrightarrow \dfrac{1}{BC} + \dfrac{1}{BD} = \dfrac{2}{BA}$.
$\blacksquare$
Teorema de Feuerbach
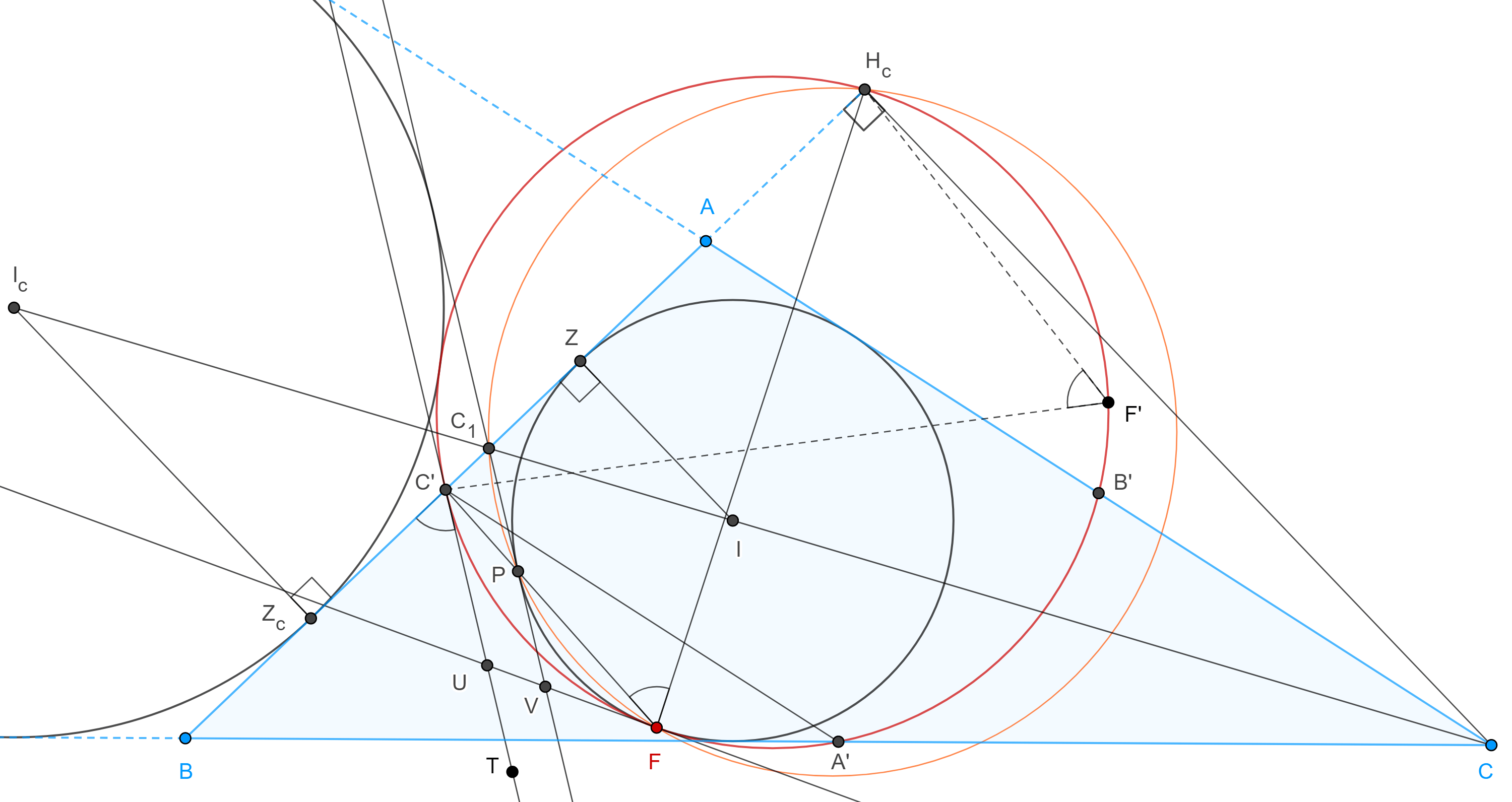
Teorema 5, de Feuerbach. La circunferencia de los nueve puntos y el incírculo de un triángulo son tangentes.
Demostración. Paso 1. Sean $\triangle ABC$, $\triangle A’B’C’$ su triangulo medial, $\Gamma(N)$ la circunferencia de los nueve puntos (el circuncírculo de $\triangle A’B’C’$) y considera la tangente $C’T$ a $\Gamma(N)$ en $C’$.
Notemos que $\angle TC’A$ y $\angle C’B’A’$ son ángulos semiinscrito e inscrito respectivamente de $\Gamma(N)$ y abarcan el mismo arco, por lo tanto, son iguales.
Recordemos que los lados de $\triangle A’B’C’$ son paralelos a los de $\triangle ABC$ y por lo tanto, $\triangle ABC$ y $\triangle A’B’C’$ son semejantes.
En consecuencia,
$\angle BC’T = \angle BC’A’ – \angle TC’A $
$= \angle BAC – \angle C’B’A’ = \angle A – \angle B$.
Paso 2. Sean $\Gamma(I)$ el incírculo de $\triangle ABC$, $C_1 = CI \cap AB$ y $C_1P$ tangente a $\Gamma(I)$ en $P$.
Como $C_1A$ y $C_1P$ son tangentes a $\Gamma(I)$ desde $C_1$ entonces $\angle PC_1I = \angle IC_1A$.
Por lo tanto,
$\angle BC_1P = \pi – \angle PC_1A $
$= \pi – (2\angle IC_1A) = \pi – 2(\pi – \angle A – \dfrac{\angle C}{2})$
$= \angle A + (\angle A + \angle C – \pi) = \angle A – \angle B$.
Así, $C’T \parallel C_1P$.
Paso 3. Sean $\Gamma(I_c)$ el excírculo opuesto al vértice $C$, $Z_c$ el punto de tangencia entre $\Gamma(I_c)$ y $AB$, $Z$ el punto de tangencia entre $\Gamma(I)$ y $AB$, $H_c$ el pie de la altura por $C$ en $\triangle ABC$.
Por el corolario 2, $(C, C_1; I, I_c) = -1$ y por la proposición 1, $(H_c, C_1; Z, Z_c) = -1$.
Recordemos que el punto medio de $Z$ y $Z_c$ coincide con el punto medio $C’$, de $AB$.
Por el teorema 4, $C’C_1 \times C’H_c = C’Z^2$.
Sea $F = C’P \cap \Gamma(I)$, $F \neq P$, por la potencia de $C’$ respecto de $\Gamma(I)$ tenemos
$C’P \times C’F = C’Z^2 = C’C_1 \times C’H_c$.
Por la ecuación anterior, el teorema de las cuerdas nos dice que $\square H_cC_1PF$ es cíclico.
Por lo tanto, $\angle H_cFP$ y $\angle PC_1H_c$ son suplementarios.
En consecuencia, $\angle H_cFC’ = \angle BC_1P = \angle BC’T$.
Por otra parte, notemos que $C’H_c$ es una cuerda de la circunferencia de los nueve puntos $\Gamma(N)$, sea $F’$ en el arco $\overset{\LARGE{\frown}}{C’H_c}$ (recorrido en ese sentido).
Entonces, $\angle BC’T + \angle TC’F’ + \angle F’C’H_c = \pi = \angle H_cF’C’ + \angle C’H_cF’ + \angle F’C’H_c$, además $\angle TC’F’ = \angle C’H_cF’$, pues abarcan el mismo arco.
Por lo tanto, los puntos $F’$ en el arco $\overset{\LARGE{\frown}}{C’H_c}$, cumplen que $\angle H_cF’C’ = \angle BC’T$, además son los únicos, siempre y cuando estén del mismo lado que $C$ respecto de $C’H_c$.
Como $F$ cumple estas características, entonces $F \in \Gamma(N)$.
Paso 4. Sean $U$ la intersección de la tangente a $\Gamma(N)$ en $F$ con $C’T$ y $V$ la intersección de la tangente a $\Gamma(I)$ en $F$ con $C_1P$.
Como $UC’ = UF$, por ser tangentes a $\Gamma(N)$ desde $U$, entonces $\angle UC’F = \angle C’FU$, igualmente vemos que $\angle VPF = \angle PFV$.
Pero $\angle UC’F = \angle VPF$ pues $C’U \parallel PV$ y $C’PF$ es transversal a ambas.
Por lo tanto, $\angle C’FU = \angle PFV = \angle C’FV$, es decir $UF$ y $VF$ son la misma recta.
Como resultado tenemos que $\Gamma(N)$ y $\Gamma(I)$ son tangentes en $F$.
$\blacksquare$
Definición 3. Al punto de tangencia entre el incírculo y la circunferencia de los nueve puntos $F$, se le conoce como punto de Feuerbach.
Más adelante…
Continuando con el tema de división armónica, en la siguiente entrada estudiaremos haces armónicos.
Tarea moral
A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.
- $i)$ Divide un segmento dado en una razón dada $\dfrac{p}{q}$,
$ii)$ Muestra que $HNGO$ es una hilera armónica, donde $H$ es el ortocentro, $N$ el centro de los nueve puntos, $G$ el centroide y $O$ el circuncentro de un triángulo. - Si los puntos $C$ y $D$ dividen internamente y externamente de manera armónica en la razón $\dfrac{p}{q}$ al segmento $AB$, muestra que el punto medio de $CD$ divide al segmento $AB$ en la razón $\dfrac{p^2}{q^2}$.
- Prueba que la suma de los cuadrados de dos segmentos armónicos es igual a cuatro veces el cuadrado de la distancia entre los puntos medios de estos segmentos.
- Considera el segmento determinado por el vértice de un triángulo y la intersección de la bisectriz interna o externa con el lado opuesto, muestra que los pies de las perpendiculares a dicha recta desde los otros dos vértices del triángulo dividen al segmento de manera armónica.
- Si los puntos $C$ y $D$ dividen armónicamente al segmento $AB$ y $O$ es el punto medio de $AB$, muestra que $OC^2 + OD^2 = CD^2 + 2OA^2$.
- Si $(A, B; C, D) = – 1$ y $A’$, $B’$ son los conjugados armónicos de $D$ respecto a los pares de puntos $(A, C)$ y $(B, C)$ respectivamente, muestra que $(A’, B’; C, D) = – 1$.
- Sean $\triangle ABC$, $D$, $E$, $F$, los puntos de tangencia del incírculo de $\triangle ABC$ con $BC$, $CA$ y $AB$ respectivamente, sea $X$ en el interior de $\triangle ABC$ tal que el incírculo de $\triangle XBC$ es tangente a $BC$, $CX$, $XB$ en $D$, $Y$, $Z$, respectivamente, demuestra que $\square EFZY$ es cíclico.
- Demuestra que la circunferencia de los nueve puntos de un triángulo es tangente a cada uno de sus excírculos.
Entradas relacionadas
- Ir a Geometría Moderna I.
- Entrada anterior del curso: Punto de Nagel.
- Siguiente entrada del curso: Haz armónico.
- Otros cursos.
Fuentes
- Altshiller, N., College Geometry. New York: Dover, 2007, pp 53-56, 166-171.
- Andreescu, T., Korsky, S. y Pohoata, C., Lemmas in Olympiad Geometry. USA: XYZ Press, 2016, pp 149-161.
- Lozanovski, S., A Beautiful Journey Through Olympiad Geometry. Version 1.4. 2020, pp 156-158.
- Johnson, R., Advanced Euclidean Geometry. New York: Dover, 2007, pp 200-203.
Agradecimientos
Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»