Introducción
En esta entrada mostraremos la existencia del punto de Nagel como el conjugado isotómico del punto de Gergonne; estudiaremos algunas propiedades de otros objetos geométricos relacionados con el punto de Nagel, a saber, la recta de Nagel, la circunferencia de Spieker y la circunferencia de Fuhrmann.
Punto de Nagel
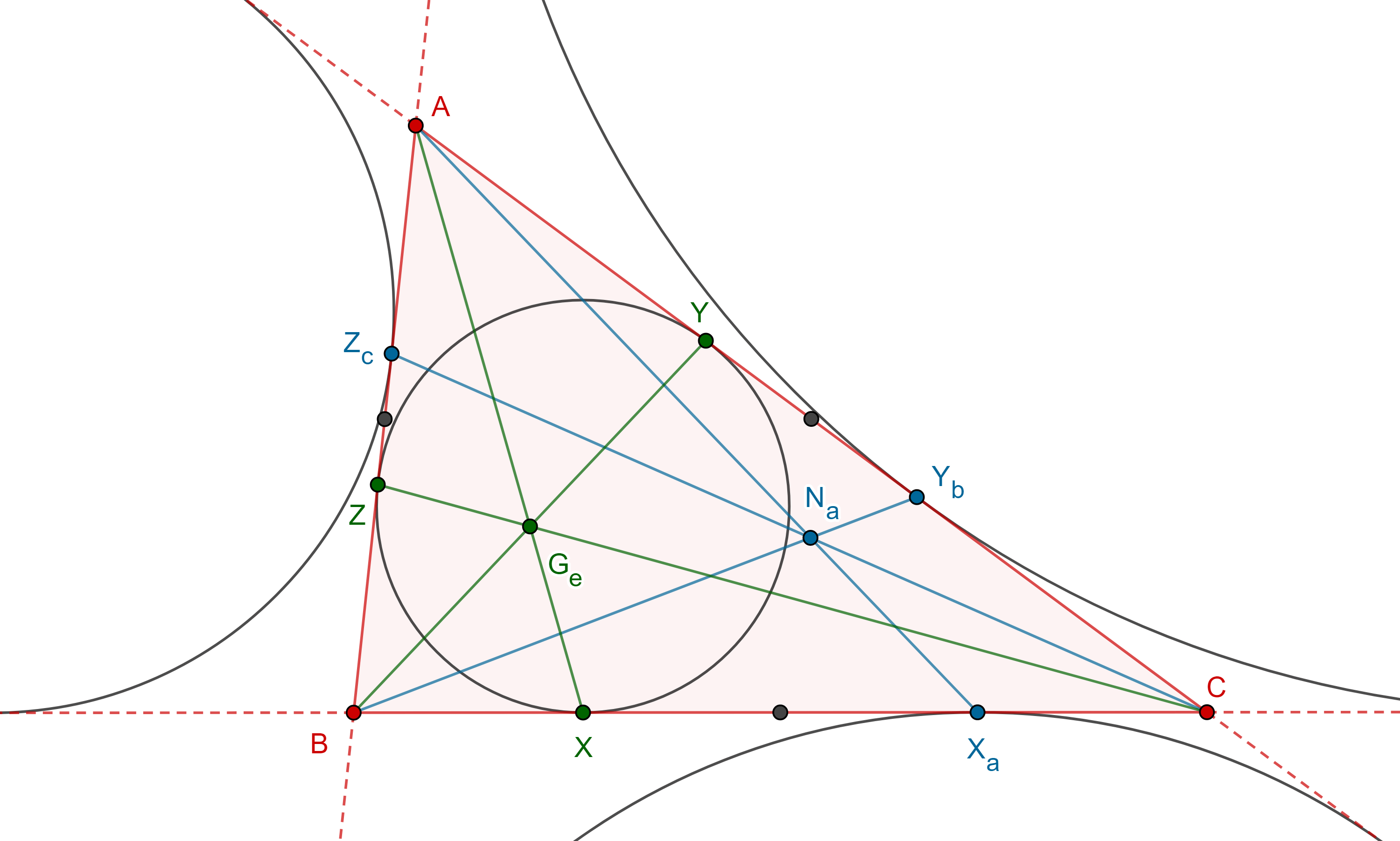
Teorema 1. Las rectas que unen los vértices de un triángulo con el punto de tangencia entre el lado opuesto y el excírculo relativo a ese lado son concurrentes, al punto de concurrencia, $N_a$, se le conoce como punto de Nagel.
Demostración. Sean $\triangle ABC$ y $X_a \in BC$, $Y_b \in CA$, $Z_c \in AB$, los puntos de tangencia de los excírculos opuestos a $A$, $B$, $C$ respectivamente
Considera $X$, $Y$ , $Z$ los puntos de tangencia del incírculo con $BC$, $CA$ y $AB$.
En la entrada triángulos en perspectiva vimos que $AX$, $BY$, $CZ$ concurren en el punto de Gergonne, $G_e$.
En la entrada circunferencias tritangentes vimos que los pares de puntos $X$, $X_a$; $Y$, $Y_b$; $Z$, $Z_b$ son puntos isotómicos, es decir, su punto medio coincide con el punto medio del lado al que pertenecen.
Por la proposición 1 de la entrada anterior, $AX_a$, $BY_b$, $CZ_c$ concurren en el conjugado isotómico de $G_e$.
$\blacksquare$
Recta de Nagel
Teorema 2.
$i)$ El incentro de un triángulo es el punto de Nagel de su triángulo medial,
$ii$) el incentro $I$, el centroide $G$ y el punto de Nagel $N_a$, de un triángulo, son colineales, a dicha recta se le conoce como recta de Nagel,
$iii)$ $IG = 2GN_a$.
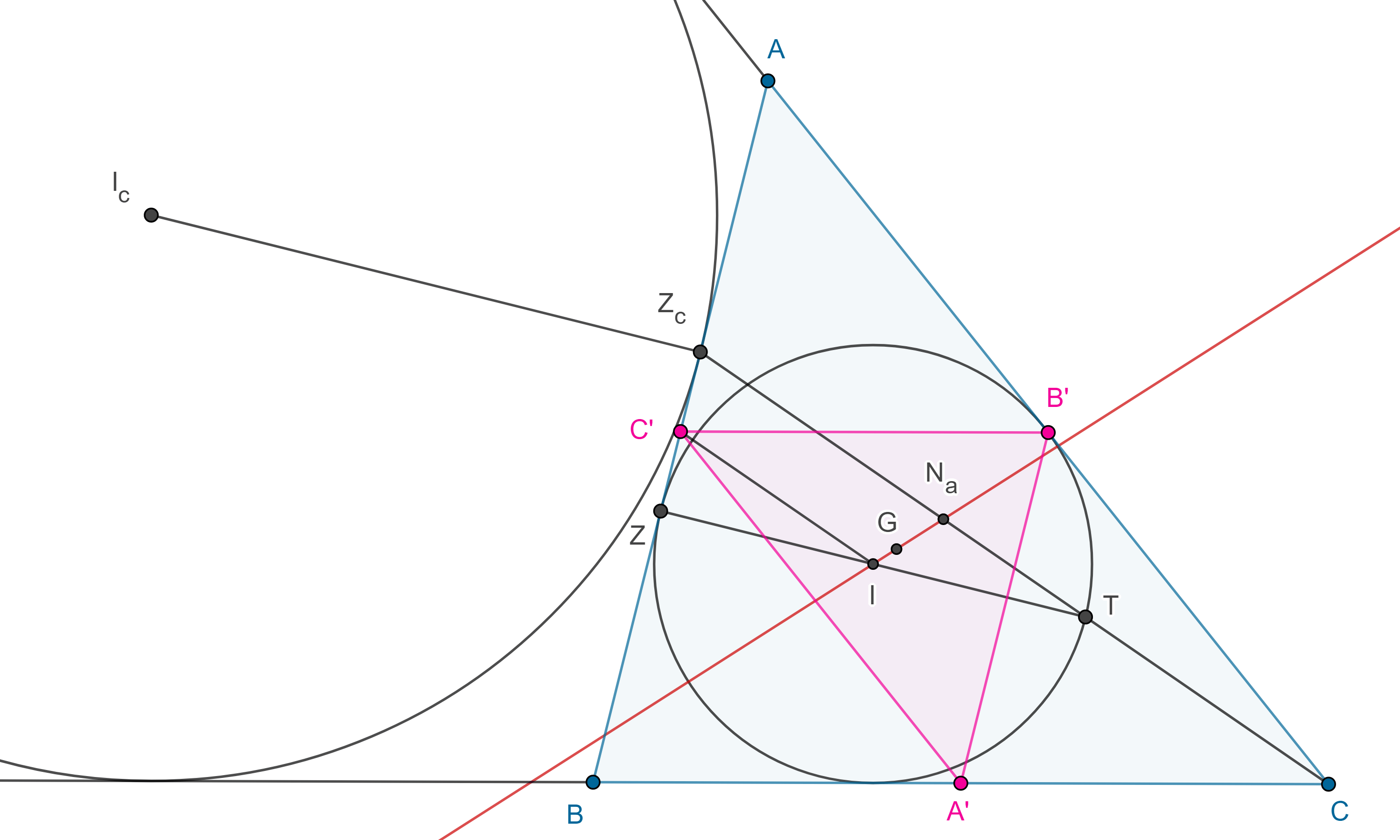
Demostración. Sean $\triangle ABC$, $\Gamma(I)$ su incírculo y $\Gamma(I_c)$ el excírculo opuesto al vértice $C$.
Considera $Z$ y $Z_c$ los puntos de tangencia de $BC$ con $\Gamma(I)$ y $\Gamma(I_c)$ respectivamente, sea $T$ el punto diametralmente opuesto a $Z$ en $\Gamma(I)$.
Como $CA$ y $BC$ son tangentes exteriores comunes a $\Gamma(I)$ y $\Gamma(I_c)$, entonces $C$ es un centro de homotecia entre $\Gamma(I)$ y $\Gamma(I_c)$.
Por otra parte, como $I$, $I_c$ son puntos correspondientes de esta homotecia y $I_cZ_c \parallel IT$ entonces $I_cZ_c$, $IT$ son rectas homotéticas.
Por lo tanto, $Z_c$ y $T$ son puntos homólogos y así, $Z_c$, $T$ y $C$ son colineales.
Ahora consideremos $\triangle A’B’C’$, el triángulo medial de $\triangle ABC$, recordemos que existe una homotecia con centro en $G$ y razón $– 2$, que lleva a $\triangle A’B’C’$ en $\triangle ABC$.
Recordemos que $Z$ y $Z_c$ son puntos isotómicos, por lo tanto, $\dfrac{ZC’}{C’Z_c} = \dfrac{ZI}{IT} = 1$, por el reciproco del teorema de Tales, $C’I \parallel Z_cT$.
Como $C’$ y $C$ son puntos homólogos de esta homotecia y $CI \parallel CZ_c$, entonces $C’I$ y $CZ_c$ son rectas homotéticas.
Como $CZ_c$ pasa por $N_a$, el punto de Nagel de $\triangle ABC$, entonces $CI$ pasa por el punto de Nagel de $\triangle A’B’C’$.
Igualmente podemos ver que $B’I$, $A’I$ pasan por el punto de Nagel de $\triangle A’B’C’$.
Por lo tanto, el incentro de $\triangle ABC$ es el punto de Nagel de $\triangle A’B’C’$.
Como los puntos notables de dos triángulos homotéticos son puntos homólogos, entonces $I$, $G$ y $N_a$ son colineales.
Dado que la razón de homotecia es $– 2$, entonces $G$ triseca al segmento $IN_a$, es decir, $IG = 2GN_a$.
$\blacksquare$
Circunferencia de Spieker
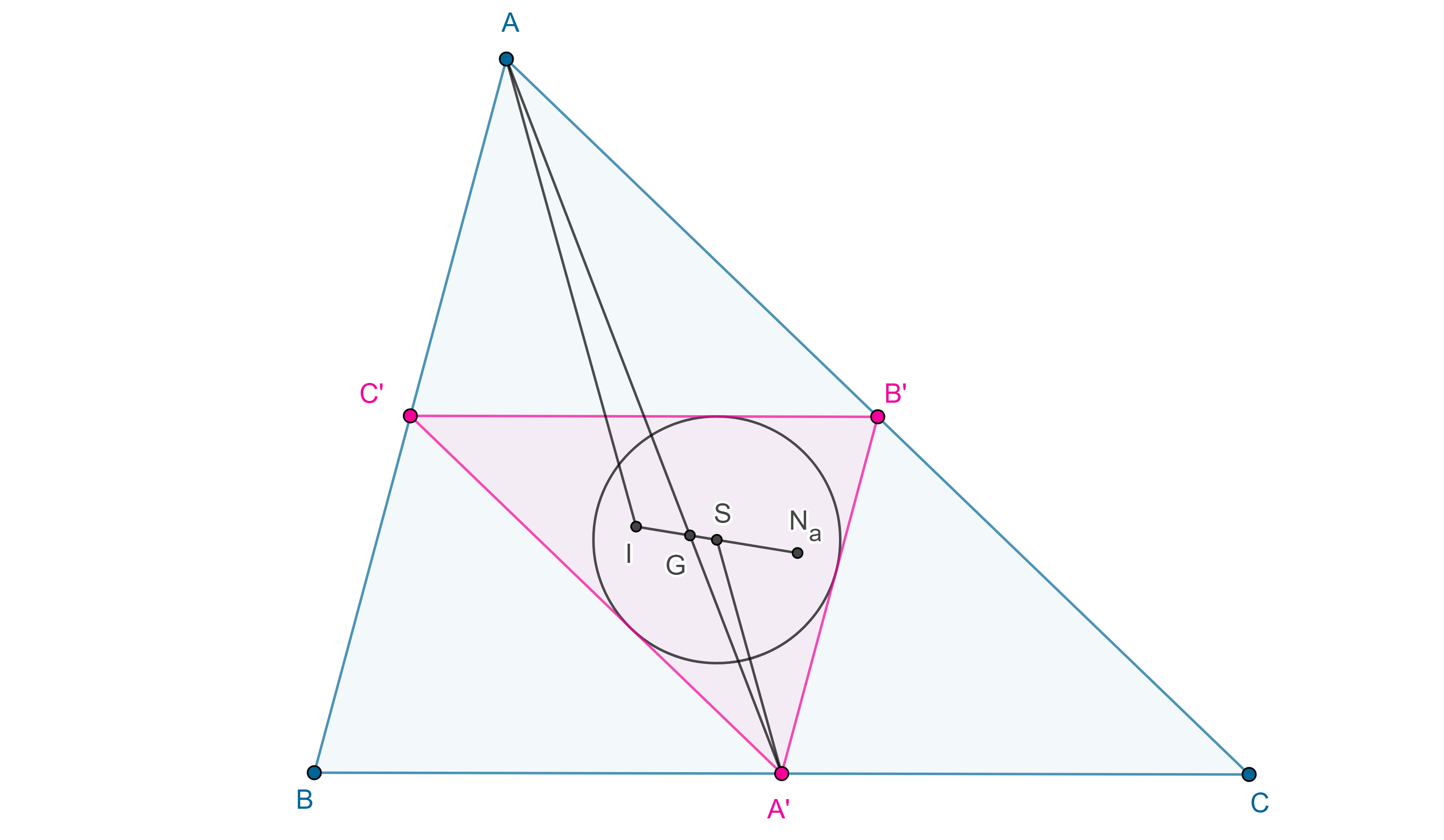
Definición 1. El incírculo del triángulo medial de un triángulo dado se conoce como circunferencia de Spieker y su centro $S$, como punto de Spieker.
Teorema 3. El punto de Spieker está en la recta de Nagel y biseca al segmento que une al incentro con el punto de Nagel.
Demostración. Sean $\triangle ABC$, $I$ el incentro, $N_a$ el punto de Nagel y consideremos $S$ el punto medio de $IN_a$.
Por el teorema anterior, $3IG = IN_a$, como $2IS = IN_a$ entonces $IG = \dfrac{2}{3}IS$, donde $G$ es el centroide de $\triangle ABC$.
Por lo tanto, $IG = 2GS$.
Sea $\triangle A’B’C’$ el triángulo medial de $\triangle ABC$, como $AG = 2GA’$, por criterio de semejanza LAL, $\triangle GAI \sim \triangle GA’S$
Por lo tanto, $\angle IAG = \angle SA’G$, es decir $AI \parallel SA’$.
Consideremos la homotecia con centro en $G$ que lleva a $\triangle ABC$ en $\triangle A’B’C’$.
Como $A$ y $A’$ son puntos correspondientes de esta homotecia, $AI \parallel A’S$ y $AI$ es bisectriz de $\angle BAC$ entonces $A’S$ es bisectriz de $\angle B’A’C’$.
Igualmente podemos ver que $B’S$ y $C’S$ son bisectrices de $\angle C’B’A’$ y $\angle A’C’B’$ respectivamente, por lo tanto, $S$ es el incentro de $\triangle A’B’C’$.
$\blacksquare$
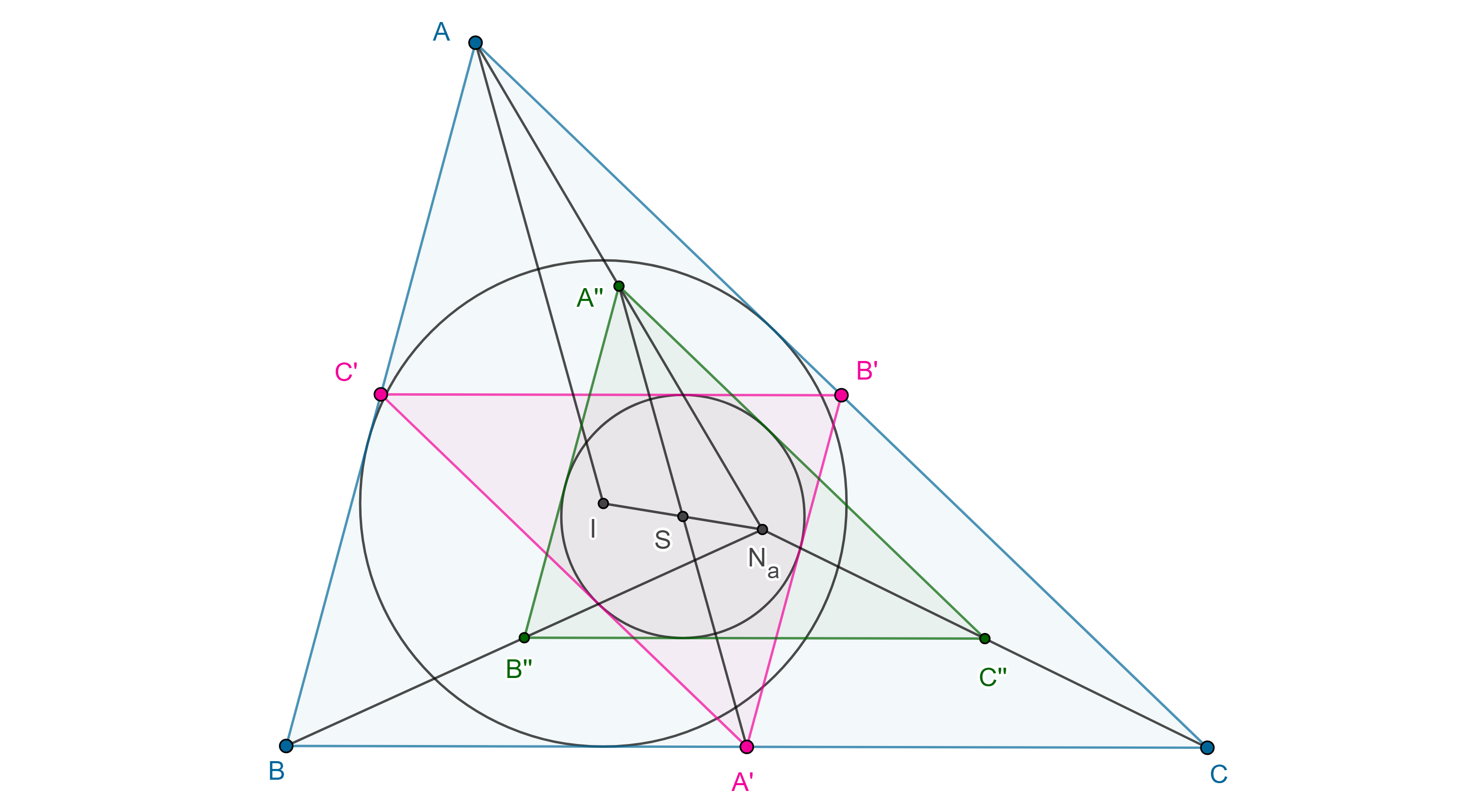
Proposición 1. La circunferencia de Spieker está inscrita en el triángulo cuyos vértices son los puntos medios de los segmentos que unen el punto de Nagel con los vértices del triángulo.
Demostración. Sean $\triangle ABC$, $N_a$ su punto de Nagel, $A’’$, $B’’$, $C’’$ los puntos medios de $AN_a$, $BN_b$, $CN_c$ respectivamente.
En $\triangle ABN_a$, $A’’B’’$ es un segmento medio por lo que $AB \parallel A’’B’’$ y $AB = 2A’’B’’$.
Igualmente podemos ver que $BC \parallel B’’C’’$, $BC = 2B’’C’’$ y $CA \parallel C’’A’’$ y $CA = 2C’’A’’$.
Como los lados de $\triangle ABC$ también son paralelos y duplican a los lados de $\triangle A’B’C’$, su triangulo medial, entonces $\triangle A’B’C’$ y $\triangle A’’B’’C’’$ son congruentes y están en homotecia.
Por otra parte, sea $I$ el incentro de $\triangle ABC$ y $S$ el punto de Spieker, en $\triangle N_aAI$, $A’’S$ es un segmento medio por lo que $A’’S \parallel AI$.
Por el teorema anterior, $A’S \parallel AI$, en consecuencia, $A’$, $S$ y $A’’$ son colineales.
De manera análoga podemos ver que $B’$, $S$, $B’’$ y $C’$, $S$, $C’’$ son colineales.
Por lo tanto, $S$ es el centro de homotecia entre $\triangle A’B’C’$ y $\triangle A’’B’’C’’$.
Como $\triangle A’B’C’$ y $\triangle A’’B’’C’’$ son congruentes y $S$ es su centro de homotecia, entonces sus incírculos coinciden.
$\blacksquare$
Corolario. El punto de Nagel es un centro de homotecia entre el incírculo y la circunferencia de Spieker de un triángulo.
Demostración. Se sigue de que $\triangle ABC$ y $\triangle A’’B’’C’’$ están en homotecia desde el punto de Nagel y que el incírculo de $\triangle A’’B’’C’’$ es la circunferencia de Spieker.
$\blacksquare$
Circunferencia de Fuhrmann
Definición 2. Considera el circuncírculo de un triángulo $\triangle ABC$, el triángulo cuyos vértices son las reflexiones de los puntos medios de los arcos $\overset{\LARGE{\frown}}{AB}$, $\overset{\LARGE{\frown}}{BC}$ y $\overset{\LARGE{\frown}}{CA}$ que no contienen a $C$, $A$ y $B$ respectivamente, se conoce como triángulo de Fuhrmann y su circuncírculo como circunferencia de Fuhrmann.
Teorema 4. El segmento que une al ortocentro con el punto de Nagel de un triángulo, es diámetro de su circunferencia de Fuhrmann.
Demostración. Sean $\triangle ABC$ y $M_a$, $M_b$, $M_c$, los puntos medios de los arcos $\overset{\LARGE{\frown}}{BC}$, $\overset{\LARGE{\frown}}{CA}$, $\overset{\LARGE{\frown}}{AB}$ respectivamente, $M’_a$, $M’_b$, $M’_c$, sus respectivas reflexiones respecto de los lados $BC$, $CA$ y $AB$.
Sean $O$ el circuncentro de $\triangle ABC$, $A’$ el punto medio de $BC$ y $M$ el punto diametralmente opuesto de $M_a$.
Notemos que $M_a$, $A’$, $O$, $M’_a$ y $M$ son colineales y entonces
$M’_aM = M_aM – M_aM’_a = 2(M_aO – M_aA’) = 2A’O$.
Por otro lado, sabemos que $AH = 2OA’$ donde $H$ es el ortocentro de $\triangle ABC$.
Como $AH = M’_aM$ y $AH \parallel M’_aM$, entonces $\square AHM’_aM$ es paralelogramo.
Ya que $M_aM$ es diámetro entonces $AM \perp AM_a$, en consecuencia, $HM’_a \perp AM_a$.
Sean $I$ el incentro, $N_a$ el punto de Nagel, $S$ el punto de Spieker, respectivamente y considera $L = N_aA’ \cap AM_a$.
Por el teorema anterior $A’S \parallel IL$ y como $S$ es el punto medio del $IN_a$ entonces $A’$ es el punto medio de $N_aL$.
Como $A’$ también es el punto medio de $M_aM’_a$ entonces $\square LM_aN_aM’_a$ es paralelogramo, es decir $M_a’N_a \parallel AM_a$.
En consecuencia, $HM’_a \perp M’_aN_a$ y por lo tanto $M’_a$ está en la circunferencia de diámetro $HN_a$.
De manera análoga vemos que $M’_b$ y $M’_c$ pertenecen a la misma circunferencia.
$\blacksquare$
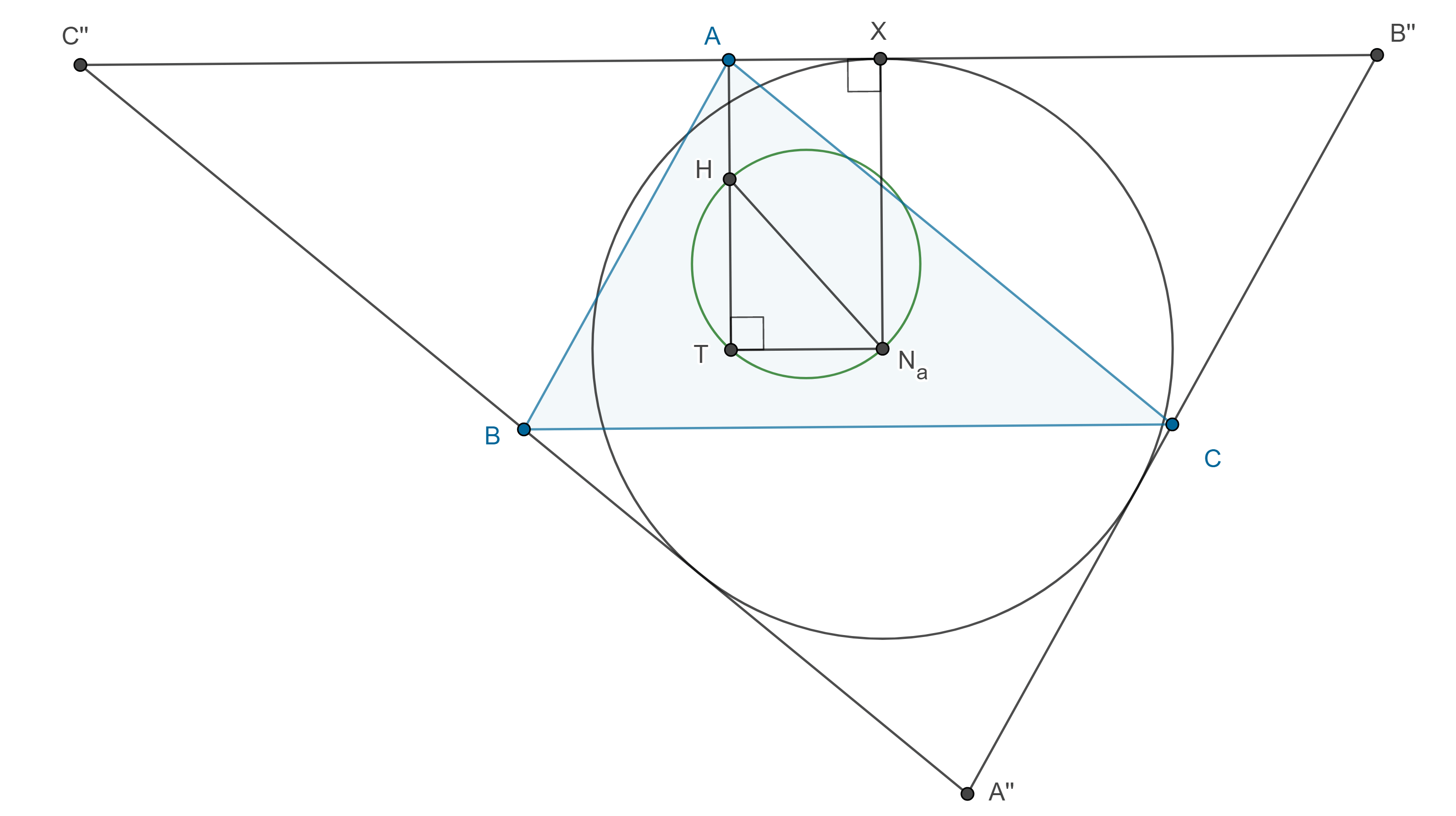
Proposición 2. La circunferencia de Fuhrmann interseca a las alturas de un triángulo, en un punto (distinto del ortocentro) que está a una distancia del vértice respectivo, del doble del inradio del triángulo.
Demostración. Sea $\triangle ABC$ y $N_a$ su punto de Nagel, consideremos $\triangle A’’B’’C’’$ su triángulo anticomplementario, el triángulo cuyos lados son paralelos a los de $\triangle ABC$ y pasan por lo vértices de $\triangle ABC$.
Como $\triangle ABC$ es el triángulo medial de $\triangle A’’B’’C’’$ entonces $N_a$ es el incentro de $\triangle A’’B’’C’’$, sea $X$ la proyección de $N_a$ en $B’’C’’$, entonces $N_aX$ es el inradio de $\triangle A’’B’’C’’$.
Por lo tanto $N_aX$ es dos veces el inradio r, de $\triangle ABC$.
Completemos el rectángulo $\square ATN_aX$ de lados $N_aX$ y $AX$, entonces $AT = 2r$ y $AT$ es la altura por $A$.
Como $H$, el ortocentro de $\triangle ABC$, está en $AT$ o su extensión y $\angle N_a TH = \dfrac{\pi}{2}$, entonces $T$ está en la circunferencia de Fuhrnamm de $\triangle ABC$.
$\blacksquare$
Más adelante…
En la próxima entrada veremos algunas propiedades de la división armónica, las cuales nos ayudaran a demostrar el teorema de Feuerbach.
Tarea moral
A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.
- Considera los puntos de tangencia de los lados de un triángulo con un excírculo, muestra que las rectas que unen los vértices del triángulo con el punto de tangencia en el lado opuesto son concurrentes.
- Prueba que la recta que pasa por el incentro y el circuncentro de un triángulo es paralela a la recta que pasa por el ortocentro y el punto de Nagel y que $HN_a = 2OI$.
- A la recta que pasa por el punto medio de un triángulo y su punto de Spieker se le conoce como cuchilla, demuestra que las tres cuchillas de un triángulo bisecan su perímetro.
- Muestra que la reflexión del incentro de un triángulo respecto del centro de los nueve puntos es el centro de su circunferencia de Fuhrmann.
- En la figura 5, muestra que $\triangle M_aM_bM_c$ y $\triangle M’_aM’_bM’_c$ son semejantes.
Entradas relacionadas
- Ir a Geometría Moderna I.
- Entrada anterior del curso: Teorema de Ceva.
- Siguiente entrada del curso: División armónica.
- Otros cursos.
Fuentes
- Altshiller, N., College Geometry. New York: Dover, 2007, pp 160-162.
- Johnson, R., Advanced Euclidean Geometry. New York: Dover, 2007, pp 225-229.
- Honsberger, R., Episodes in Nineteenth and Twentieth Century Euclidean Geometry. Washington: The Mathematical Association of America, 1995, pp 49-52.
- University of Crete
- Wolfram MathWorld
- Wikipedia
Agradecimientos
Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»