Archivo de la etiqueta: límite

Cálculo Diferencial e Integral I: Límites en el infinito

Por Juan Manuel Naranjo Jurado

Deja un comentario

Introducción

Previamente se revisó el concepto de límite de una función, así como el de límites laterales. En la revisión de estos temas nos habíamos enfocado en revisar el límite de una función $f$ en un punto $x_0$. Ahora ampliaremos el concepto estudiando $f$ para el caso cuando $x$ tiende a infinito.

Límite en el infinito

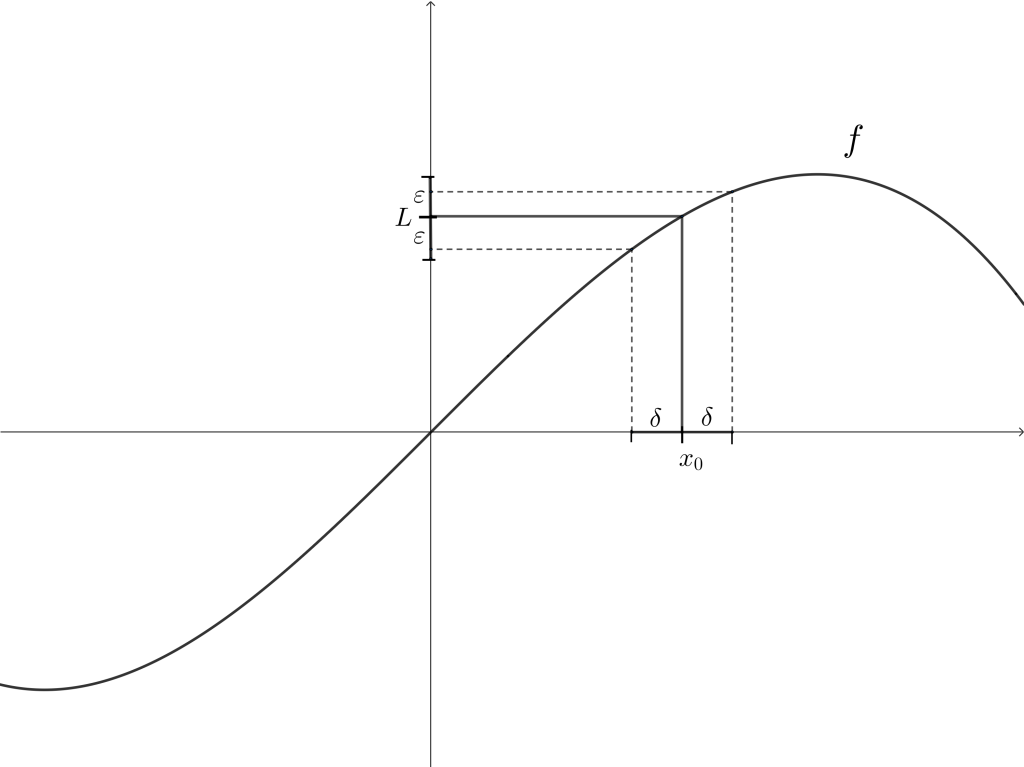
La intuición detrás de la definición de límite en el infinito es que $f$ tiene límite $L$ cuando $x$ tiende a infinito si para valores lo suficientemente grandes de $x$ nos acercamos arbitrariamente a $L.$

Definición. Sea $f: A \rightarrow \mathbb{R}$. Decimos que $f$ tiende al límite $L \in \mathbb{R}$ cuando $x$ tiende a infinito si para cualquier $\varepsilon > 0$ existe $M \in \mathbb{R}$, tal que para cualquier $x>M$, se tiene que $|f(x)-L|<\varepsilon$ y lo denotamos $$\lim_{x \to \infty} f(x) = L.$$

Ejemplo 1. Prueba que $$\lim_{x \to \infty} \frac{1}{x} = 0.$$
Demostración.

Sea $\varepsilon > 0$ y tomemos $M = \frac{1}{\varepsilon}$. De esta forma, para todo $x > M$ se tiene que $x > \frac{1}{\varepsilon}$, y por lo tanto $-\varepsilon < 0 <\frac{1}{x} < \varepsilon$, es decir, $|\frac{1}{x}-0|< \varepsilon.$
$$\therefore \lim_{x \to \infty} \frac{1}{x} = 0.$$

$\square$

Podemos observar que la definición es bastante natural una vez hemos entendido el concepto de límite, por lo cual procederemos directamente a revisar algunas de sus propiedades.

Propiedades de los límites en el infinito

Al igual que la definición revisada para el límite de una función en un punto, el límite de una función cuando $x$ tiende a infinito también es único.

Proposición. El límite de una función cuando $x$ tiende a infinito es único, es decir, si $f$ tiende a $L$ cuando $x \rightarrow \infty$ y $f$ tiende a $L’$ cuando $x \rightarrow \infty$, entonces $L = L’.$

La demostración es muy similar a la realizada en la entrada de definición formal del límite, por lo cual se omitirá, pero de ser necesario puedes realizarla para repasar los conceptos.

Análogamente a las entradas anteriores, tenemos una relación entre el límite al infinito de una función y el límite de una sucesión.

Teorema. Sea $f: A \rightarrow \mathbb{R}$. Los siguientes enunciados son equivalentes.

  1. $$\lim_{x \to \infty} f(x) = L.$$
  2. Para cualquier sucesión $\{a_n\}$ en $A$ que diverge a infinito se tiene que la sucesión $\{f(a_n)\}$ converge a $L.$

Notemos que para que el límite en el infinito tenga sentido, se debe cumplir que $(a, \infty) \subset A$ para algún $a \in \mathbb{R}.$

Demostración.

$1) \Rightarrow 2)]$ Sea $\varepsilon >0$. Supongamos que $$\lim_{x \to \infty} f(x) = L.$$
Y sea $\{ a_n \}$ en $A$ que diverge a infinito.

Por hipótesis $f$ tiende a $L$ cuando $x$ tiende a infinito, entonces existe $M \in \mathbb{R}$ tal que si $x > M$ se tiene que $|f(x)-L| < \varepsilon.$

Además, como $\{a_n\}$ diverge a infinito, entonces para $M$ existe $n_0 \in \mathbb{N}$ tal que si $n \geq n_0$ se tiene que $a_n > M.$ Por lo tanto, $|f(a_n)-L| < \varepsilon.$
$$\therefore \lim_{n \to \infty} f(a_n) = L.$$


$1) \Leftarrow 2)]$ Realizaremos esta demostración por contrapositiva, es decir, probaremos que si $$\lim\limits_{x \to \infty} f(x) \neq L,$$

entonces existe $\{a_n\}$ en $A$ tal que $$\lim\limits_{n \to \infty} a_n = \infty \qquad \text{ y } \qquad \lim\limits_{n \to \infty} f(a_n) \neq L.$$

Supongamos que $\lim\limits_{x \to \infty} f(x) \neq L$. Entonces existe $\varepsilon > 0$ tal que para todo $M_n > a$ existe $x’_n > M_n$ tal que $|f(x’_n) -L| \geq \varepsilon.$

De esta forma, es posible generar la sucesión $\{ x’_n \}$ en $A.$ Primero veremos que esta sucesión diverge a infinito.

Sea $\alpha \in \mathbb{R}$. Entonces existe $M_{n_0} \in \mathbb{R}$ tal que $M_{n_0} > \alpha$. Además, $x’_{n_0} > M_{n_0} > \alpha$, y por lo tanto para todo $n \geq n_0$ se sigue que $x’_n > M_n \geq M_{n_0} > \alpha$. Es decir, $x’_n > \alpha$ para todo $n \geq n_0$.

$$\therefore \lim_{n \to \infty} x’_n = \infty.$$

Además, se tiene que $|f(x’_n)-L| \geq \varepsilon$ para todo $n \in \mathbb{N}$.

Consideremos $\{a_n\} = \{x’_n\}$, entonces

$$\lim\limits_{n \to \infty} a_n = \infty \qquad \text{ y } \qquad \lim\limits_{n \to \infty} f(a_n) \neq L.$$

Por lo tanto, concluimos que $2) \Rightarrow 1)$

$\square$

Después de este teorema, nuevamente logramos obtener las mismas propiedades que conocemos del límite de una sucesión.

Proposición. Sean $f: A \rightarrow \mathbb{R}$, $g: A \rightarrow \mathbb{R}$ con $A \subset \mathbb{R}$ tal que $(a, \infty) \subset A$ para algún $a \in \mathbb{R}$. Si además

$$\lim_{x \to \infty} f(x) = L \quad \text{ y } \quad \lim_{x \to \infty} g(x) = T$$

entonces

  1. $$\lim_{x \to \infty} c \cdot f(x) = cL.$$
  2. $$\lim_{x \to \infty} (f+g)(x) = L+T.$$
  3. $$\lim_{x \to \infty} (f-g)(x) = L-T.$$
  4. $$\lim_{x \to \infty} (f \cdot g)(x) = LT.$$
  5. Si $T \neq 0$ y $g(x) \neq 0$ para $x > a$, entonces $$\lim_{x \to \infty} \frac{f}{g}(x) = \frac{L}{T}.$$

Ahora veremos una proposición que nos será útil para el cálculo de límites.

Proposición. Para todo $k \in \mathbb{N}$ se tiene que $$\lim_{x \to \infty} \frac{1}{x^k} = 0.$$

Demostración.

Procederemos a realizar esta demostración mediante inducción.
Caso base: $k = 1$.
En el ejemplo anterior se probó mediante la definición que $$\lim_{x \to \infty} \frac{1}{x^1} = \lim_{x \to \infty} \frac{1}{x} = 0.$$
Hipótesis de inducción: $$\lim_{x \to \infty} \frac{1}{x^k} = 0.$$
Ahora veamos que también se cumple para $k+1$.

\begin{align*}
\lim_{x \to \infty} \frac{1}{x^{k+1}} = & \lim_{x \to \infty} \frac{1}{x^k} \cdot \frac{1}{x^1} \\ \\
= & \lim_{x \to \infty} \frac{1}{x^k} \lim_{x \to \infty} \frac{1}{x^1} \\ \\
= & 0 \cdot 0 = 0.
\end{align*}

\begin{gather*}
\therefore \lim_{x \to \infty} \frac{1}{x^{k+1}} = 0. \\ \\
\therefore \lim_{x \to \infty} \frac{1}{x^k} = 0 \text{, } \forall k \in \mathbb{N}.
\end{gather*}

$\square$

Revisaremos un par de ejemplos donde aplicaremos las propiedades enunciadas.

Ejemplo 2. Determina $$\lim_{x \to \infty} \frac{8x+5}{x^3+10}.$$

Notemos que
\begin{align*}
\lim_{x \to \infty} \frac{8x+5}{x^3+10} = & \lim_{x \to \infty} \frac{8x+5}{x^3+10} \cdot \frac{\frac{1}{x^3}}{\frac{1}{x^3}} \\ \\
= & \lim_{x \to \infty} \frac{\frac{8x}{x^3} + \frac{5}{x^3}}{\frac{x^3}{x^3}+\frac{10}{x^3}} \\ \\
= & \lim_{x \to \infty} \frac{\frac{8}{x^2} + \frac{5}{x^3}}{1+\frac{10}{x^3}} \\ \\
= & \frac{\lim\limits_{x \to \infty} \frac{8}{x^2} + \frac{5}{x^3}}{\lim\limits_{x \to \infty} 1+\frac{10}{x^3}} \\ \\
= & \frac{0 + 0}{1+0} \\ \\
= & \frac{0}{1} \\ \\
= & 0.
\end{align*}
$$\therefore \lim_{x \to \infty} \frac{8x+5}{x^3+10} = 0.$$

Ejemplo 3. Calcula el siguiente límite $$\lim_{x \to \infty} \frac{1}{\sqrt{x^2-2x}-x}.$$

Como consideraremos que $x \rightarrow \infty$, podemos suponer, particularmente, que $x>0$, entonces

\begin{align*}
\frac{1}{\sqrt{x^2-2x}-x} = & \frac{1}{\sqrt{x^2-2x}-x} \cdot \frac{\sqrt{x^2-2x}+x}{\sqrt{x^2-2x}+x} \\ \\
= & \frac{\sqrt{x^2-2x}+x}{\left( \sqrt{x^2-2x} \right)^2 – x^2}\\ \\
= & \frac{\sqrt{x^2-2x}+x}{x^2-2x – x^2} \\ \\
= & \frac{\sqrt{x^2-2x}+x}{-2x} \\ \\
= & -\frac{\sqrt{x^2-2x}}{2x} – \frac{x}{2x} \\ \\
= & -\frac{\sqrt{x^2-2x}}{\sqrt{4x^2}} – \frac{1}{2} \text{, como $x$ es positivo, $\sqrt{4x^2} = |2x| = 2x$ } \\ \\
= & -\sqrt{\frac{x^2-2x}{4x^2}} – \frac{1}{2} \\ \\
= & -\sqrt{\frac{x^2}{4x^2} – \frac{2x}{4x^2}} – \frac{1}{2} \\ \\
= & -\sqrt{\frac{1}{4} – \frac{1}{2x}} – \frac{1}{2}.
\end{align*}
$$\Rightarrow \frac{1}{\sqrt{x^2-2x}-x} = -\sqrt{\frac{1}{4} – \frac{1}{2x}} – \frac{1}{2}.$$

Entonces tenemos que
\begin{align*}
\lim_{x \to \infty} \frac{1}{\sqrt{x^2-2x}-x} = & \lim_{x \to \infty} \left( -\sqrt{\frac{1}{4} – \frac{1}{2x}} – \frac{1}{2} \right) \\
= & -\sqrt{\frac{1}{4} – 0} – \frac{1}{2} \\
= & -\frac{1}{2} -\frac{1}{2} \\
= & -1.
\end{align*}
$$\therefore \lim_{x \to \infty} \frac{1}{\sqrt{x^2-2x}-x} = -1.$$

A continuación enunciaremos el teorema del sándwich para este tipo de límites.

Proposición. Sean $f$, $g$, $h: A \rightarrow \mathbb{R}$ con $A \subset \mathbb{R}$ tal que $(a, \infty) \subset A$ para algún $a \in \mathbb{R}$. Si existe $M_1 \in \mathbb{R}$ tal que para todo $x >M_1$ se tiene que $$f(x) \leq g(x) \leq h(x) \quad \text{ y } \quad \lim_{x \to \infty} f(x) = L = \lim_{x \to \infty} h(x).$$

Entonces $$ \lim_{x \to \infty} g(x) = L.$$

Nuevamente, omitiremos la demostración pues es análoga a la revisada en una entrada anterior.

Extensión del límite en el infinito

Así como tenemos el límite en el infinito, existe una definición análoga que considera el límite de una función cuando $x$ tiende a $- \infty$.

Definición. Sean $A \subseteq \mathbb{R}$ y $f: A \rightarrow \mathbb{R}$. Decimos que $f$ tiende al límite $L \in \mathbb{R}$ cuando $x$ tiende a $- \infty$ si para cualquier $\varepsilon > 0$ existe $m \in \mathbb{R}$, tal que para cualquier $x<m$, se tiene que $|f(x)-L|<\varepsilon$ y lo denotamos $$\lim_{x \to -\infty} f(x) = L.$$

La definición nos indica que $f$ tiene límite $L$ cuando $x$ tiende a $-\infty$ si para valores lo suficientemente pequeños de $x$ nos acercamos arbitrariamente a $L$.

Esta extensión de límite tiene propiedades análogas revisadas en esta entrada.

Más adelante…

En la siguiente entrada revisaremos una nueva variante del límite de una función: los límites infinitos. Es decir, veremos el caso donde el límite de una función es infinito.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  • Demostrar que si $f: A \rightarrow \mathbb{R}$ es tal que $$\lim_{x \to \infty} x f(x) = L$$ con $L \in \mathbb{R}$, entonces $$\lim_{x \to \infty} f(x) = 0.$$
  • Sean $f$ y $g$ dos funciones definidas en $(a, \infty)$ tales que $$\lim_{x \to \infty} f(x) = L \quad \text{ y } \quad \lim_{x \to \infty} g(x) = \infty.$$
    Entonces se tiene que $$\lim_{x \to \infty} f(g(x)) = L.$$
  • Prueba que $$\lim_{x \to \infty} f(x) = \lim_{x \to -\infty} f(-x).$$
  • Prueba que $$\lim_{x \to 0^-} f(\frac{1}{x}) = \lim_{x \to -\infty} f(x).$$
  • Calcula los siguientes límites
    $i$) $$\lim_{x \to \infty} \frac{\sqrt{x+1}}{x} \text{, definido para } x >0.$$
    $ii$) $$\lim_{x \to \infty} \frac{\sqrt{x}-x}{\sqrt{x}+x} \text{, definido para } x >0.$$

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Cálculo Diferencial e Integral I: Límites laterales

Por Juan Manuel Naranjo Jurado

Deja un comentario

Introducción

En las entradas anteriores hemos trabajado con la definición de límite y revisamos sus propiedades. En esta ocasión, daremos la definición de límite por la derecha y límite por la izquierda, que en conjunto son llamados límites laterales. De igual forma, revisaremos algunos ejemplos y su relación con la definición vista anteriormente.

Límites laterales

Las definiciones que veremos a continuación se basan en restringir la forma en que nos acercamos a $x_0.$ El límite por la derecha se enfoca en acercarnos por la derecha, es decir, pediremos que $x > x_0,$ lo cual se traducirá en que debe cumplirse que $0<x-x_0 < \delta$. Por otro lado, para el límite por la izquierda debe cumplirse que $x < x_0,$ de esta forma se tendrá que $0<x_0-x< \delta.$ Primero daremos la definición de límite por la derecha.

Definición. Sean $A \subset \mathbb{R}$ y $f: A \rightarrow \mathbb{R}.$ Se dice que $L \in \mathbb{R}$ es límite por la derecha de $f$ en $x_0,$ si para todo $\varepsilon >0$ existe $\delta > 0$ tal que si $0<x-x_0<\delta$ entonces $|f(x)-L| < \varepsilon.$ Cuando $L$ es el límite de $f$ en el punto $x_0$ por la derecha, lo denotamos $$\lim_{x \to x_0+} f(x) = L.$$

Análogamente, tenemos la definición de límite por la izquierda.

Definición. Sean $A \subset \mathbb{R}$ y $f: A \rightarrow \mathbb{R}.$ Se dice que $L \in \mathbb{R}$ es límite por la izquierda de $f$ en $x_0,$ si para todo $\varepsilon >0$ existe $\delta > 0$ tal que si $0<x_0 – x<\delta$ entonces $|f(x)-L| < \varepsilon.$ Cuando $L$ es el límite de $f$ en el punto $x_0$ por la izquierda, lo denotamos $$\lim_{x \to x_0-} f(x) = L.$$

Propiedades de los límites laterales

De forma similar al teorema que vimos para los límites, existe una relación entre el límite lateral de una función y el límite de una sucesión, basta agregar a los supuestos la condición de que la sucesión sea mayor que $x_0$ para todo $n \in \mathbb{N}$ en el caso de límite por la derecha y que sea menor que $x_0$ para todo $n \in \mathbb{N}$ en el caso de límite por la izquierda.

Teorema. Sea $A \subset \mathbb{R}.$ Definimos la función $f:A \rightarrow \mathbb{R}.$ Entonces, dado un $x_0,$ los siguientes enunciados son equivalentes.

  1. $$\lim_{x \to x_0+} f(x) = L.$$
  2. Para toda sucesión $\{ a_n \}$ en $A$ que converge a $x_0$ y tal que $a_n > x_0$ para todo $n\in \mathbb{N},$ la sucesión $\{f(a_n)\}$ converge a $L.$

El teorema de límite por la izquierda es similar al anterior. Además, la demostración es totalmente análoga a la revisada en una entrada anterior por lo cual quedará como tarea moral. También recordemos que este teorema nos ayuda a determinar las propiedades que tienen los límites laterales debido a la herencia que nos brinda el límite de una sucesión; es gracias a ello que podremos hacer uso de tales propiedades en los siguientes ejemplos.

Ejemplo 1. Sea $f: \mathbb{R} \rightarrow \mathbb{R},$ definida de la siguiente forma

$$f(x) =
\begin{cases}
x^3+1 & \quad \text{si } x<-1 \\
x^2+1& \quad \text{si } x \geq -1. \\
\end{cases}
$$

Determina los límites laterales en $x_0 = -1.$

Primero mostraremos la gráfica de la función:

Calculando el límite por la izquierda, tenemos
$$\lim_{x \to -1^-} f(x) = \lim_{x \to -1^-} x^3+1 = 0.$$

Por otro lado, el límite por la derecha
$$\lim_{x \to -1^+} f(x) = \lim_{x \to -1^+} x^2+1= 2.$$

Por lo tanto
$$\lim_{x \to 0^-} f(x) = 0 \quad \text{ y } \quad \lim_{x \to 0^+} f(x) = 2.$$

Ejemplo 2. Sea $f: \mathbb{R} \setminus \{0 \} \rightarrow \mathbb{R}.$ Calcula los límites laterales en $x_0 = 0$ de

$$f(x) = \frac{|x|}{x}.$$

La gráfica de la función es la siguiente:

Calculando el límite por la izquierda, tenemos
\begin{align*}
\lim_{x \to 0^-} f(x) = & \lim_{x \to 0^-} \frac{|x|}{x} \\
= & \lim_{x \to 0^-} \frac{-x}{x} \text{, pues $x$ < 0} \\
= & \lim_{x \to 0^-} -1 \\
= & -1.
\end{align*}
Por otro lado, el límite por la derecha
\begin{align*}
\lim_{x \to 0^+} f(x) = & \lim_{x \to 0^+} \frac{|x|}{x} \\
= & \lim_{x \to 0^+} \frac{x}{x} \text{, pues $x$ > 0} \\
= & \lim_{x \to 0^+} 1 \\
= & 1.
\end{align*}
Por lo tanto
$$\lim_{x \to 0^-} f(x) = -1 \quad \text{ y } \quad \lim_{x \to 0^+} f(x) = 1.$$

De los ejemplos revisados, el primero tiene la propiedad de que sus límites laterales son iguales mientras que para el segundo y el tercero tales límites son distintos en $x_0.$

Relación entre el límite de una función y sus límites laterales

Parece inmediato inferir que, considerando un punto $x_0$ dado, si los límites por la izquierda y por la derecha existen y son iguales, entonces el límite de la función sí existe en tal punto. De la misma manera, resulta natural que si el límite existe, entonces los límites laterales también existen y son iguales. Probaremos esta equivalencia, pero para hacerlo, primero demostraremos la siguiente proposición.

Proposición. Sean $x,$ $x_0$ en $\mathbb{R}$ y $\delta >0.$ Entonces $0<|x-x_0|< \delta$ si y solo si $0<x-x_0<\delta \quad$ ó $\quad 0<x_0-x<\delta.$

Demostración.
Supongamos que $0<|x-x_0|< \delta$.

Caso 1: $x-x_0 > 0$.
Entonces $|x-x_0| = x-x_0$, así
\begin{gather*}
0<|x-x_0|< \delta \Leftrightarrow 0< x-x_0 < \delta.
\end{gather*}

Caso 2: $x- x_0 < 0$.
Entonces $|x-x_0| = x_0-x$, así
\begin{gather*}
0<|x-x_0| < \delta \Leftrightarrow 0< x_0-x < \delta.
\end{gather*}

$$\therefore 0<|x-x_0|< \delta \Leftrightarrow 0<x-x_0<\delta \quad \text{ ó } \quad 0<x_0-x<\delta.$$

$\square$

Teorema. El límite de una función $f$ en el punto $x_0$ existe y es igual a $L$ si y solo si los límites laterales existen y son iguales a $L$, es decir

$$\lim_{x \to x_0} f(x) = L \quad \Leftrightarrow \quad \lim_{x \to x_0^+} f(x) = L = \lim_{x \to x_0^-} f(x).$$

Demostración.

$\Rightarrow]$ Supongamos que $$\lim_{x \to x_0} f(x) = L.$$
Sea $\varepsilon > 0$. Como $f$ converge a $L$ en $x_0$, existe $\delta > 0$ tal que si $0<|x-x_0|< \delta$ se tiene que $|f(x)-L| < \varepsilon.$

Si $0<x-x_0 < \delta$, entonces $0<|x-x_0|< \delta$ por la proposición anterior. Se sigue que
\begin{gather*}
|f(x)-L| < \varepsilon. \\
\therefore \lim_{x \to x_0^+} f(x) = L.
\end{gather*}

Si $0<x_0-x < \delta$, entonces $0<|x-x_0|< \delta$ por la proposición anterior. Se sigue que
\begin{gather*}
|f(x)-L| < \varepsilon. \\
\therefore \lim_{x \to x_0^-} f(x) = L.
\end{gather*}

$\Leftarrow]$ Supongamos que $$\lim_{x \to x_0^+} f(x) = L = \lim_{x \to x_0^-} f(x)$$
Sea $\varepsilon > 0.$

Como $\lim\limits_{x \to x_0^+} f(x) = L$, existe $\delta_1$ tal que si $0<x-x_0<\delta_1$ entonces $|f(x)-L| < \varepsilon.$

Como $\lim\limits_{x \to x_0^-} f(x) = L$, existe $\delta_2$ tal que si $0<x_0-x<\delta_2$ entonces $|f(x)-L| < \varepsilon.$

Consideremos $\delta = min \{ \delta_1, \delta_2\}.$ Por la proposición, si $0<|x-x_0|< \delta$, entonces $0<x-x_0<\delta$ ó $0<x_0-x<\delta.$

Para el primer caso, tenemos que $0<x-x_0<\delta \leq \delta_1$, entonces $|f(x)-L| < \varepsilon.$
Para el segundo caso, se tiene que $0<x_0-x<\delta \leq \delta_2$, entonces $|f(x)-L| < \varepsilon.$

Por lo tanto $$\lim_{x \to x_0} f(x) = L.$$

$$\therefore \lim_{x \to x_0} f(x) = L \quad \Leftrightarrow \quad \lim_{x \to x_0^+} f(x) = L = \lim_{x \to x_0^-} f(x).$$

$\square$

Observación. Ya que hemos demostrado este teorema, podemos notar que si los límites laterales de una función son distintos en un punto $x_0$, entonces no existe el límite de la función en tal punto.

Finalizaremos esta entrada revisando los siguientes ejemplos.

Ejemplo 3. Determina si existe el límite en $x_0 = 0$ para la siguiente función $$f(x) = x \sqrt{\frac{1}{4x^2}-16}.$$

Veamos primero qué sucede con el límite por la izquierda
\begin{align*}
\lim_{x \to 0^-} f(x) = & \lim_{x \to 0^-} x \sqrt{\frac{1}{4x^2}-16} \\ \\
= & \lim_{x \to 0^-} x \sqrt{\frac{1-64x^2}{4x^2}} \\ \\
= & \lim_{x \to 0^-} \frac{ x \sqrt{1-64x^2} }{ \sqrt{4x^2} } \\ \\
= & \lim_{x \to 0^-} \frac{ x \sqrt{1-64x^2} }{ 2|x|} \\ \\
= & \lim_{x \to 0^-} \frac{ x \sqrt{1-64x^2} }{ -2x} \text{, pues $x$ < 0} \\ \\
= & \lim_{x \to 0^-} – \frac{\sqrt{1-64x^2} }{2} \\ \\
= & – \frac{1}{2}.
\end{align*}

De forma similar, tenemos que
\begin{align*}
\lim_{x \to 0^+} f(x) = & \lim_{x \to 0^+} x \sqrt{\frac{1}{4x^2}-16} \\ \\
= & \lim_{x \to 0^+} x \sqrt{\frac{1-64x^2}{4x^2}} \\ \\
= & \lim_{x \to 0^+} \frac{ x \sqrt{1-64x^2} }{ 2x} \text{, pues $x$ > 0} \\ \\
= & \lim_{x \to 0^+} \frac{\sqrt{1-64x^2} }{2} \\ \\
= & \frac{1}{2}.
\end{align*}
$$\therefore \lim_{x \to 0^-} f(x) = -\frac{1}{2} \quad \text{ y } \quad \lim_{x \to 0^+} f(x) = \frac{1}{2}.$$

Como los límites laterales son distintos, podemos concluir que el límite de la función $f$ no existe en el punto $x_0 = 0.$

Ejemplo 4. Sea $f: \mathbb{R} \rightarrow \mathbb{R}$, definida de la siguiente forma
$$f(x) =
\begin{cases}
x^2 & \quad \text{si } x<5 \\
2x+15 & \quad \text{si } x \geq 5. \\
\end{cases}
$$
Determina si el límite existe en $x_0 = 5.$

Iniciemos calculando el límite por la izquierda.
$$\lim_{x \to 5^-} f(x) = \lim_{x \to 5^-} x^2 = 25.$$

Por otro lado, el límite por la derecha
$$\lim_{x \to 5^+} f(x) = \lim_{x \to 5^+} 2x+15 = 25.$$

Por lo tanto
$$\lim_{x \to 0^-} f(x) = 25 \quad \text{ y } \quad \lim_{x \to 0^+} f(x) = 25.$$

Como los límites laterales existen y son iguales, podemos concluir que
$$\lim_{x \to 0} f(x) = 25.$$

Más adelante…

¿Qué sucede cuando en lugar de acercarnos a un punto en particular $x_0$, hacemos que $x$ crezca indefinidamente? Esto y otras ampliaciones del concepto del límite serán revisadas en la siguiente entrada con lo cual estaremos listos para calcular todo tipo de límites y, con ello, podremos conocer el comportamiento que toman las funciones tanto en un punto específico como «en el infinito».

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  • Demuestra que
    $i$) $\lim_\limits{x \to 0^+} f(x) = \lim_\limits{x \to 0^-} f(-x).$
    $ii$) $\lim_\limits{x \to 0} f(|x|) = \lim_\limits{x \to 0^+} f(x).$
  • Usando la definición épsilon-delta de límite por la derecha, prueba que $\lim_{x \to 8^+} \sqrt{x-8} = 0.$
  • Calcula el límite en $x_0 = 5$ de la función
    $$f(x) =
    \begin{cases}
    \frac{x^2-12x+35}{x-5} & \quad \text{si } x < 5 \\
    \frac{x-5}{1- \sqrt{x-4} } & \quad \text{si } x \geq 5.
    \end{cases}
    $$
  • Usando límites laterales, determina si existe $$\lim_{x \to 0} \frac{3x + |x|}{7x-5|x|}.$$

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Cálculo Diferencial e Integral I: Teoremas sobre el límite de una función

Por Juan Manuel Naranjo Jurado

Deja un comentario

Introducción

Después de haber revisado algunos ejemplos de límite de funciones, estamos listos para conocer y demostrar algunas de las propiedades; para este fin, usaremos la relación existente entre el límite de una función y el de una sucesión demostrada en la entrada anterior.

Teoremas sobre el límite de una función

Considerando el criterio de sucesiones para límites visto anteriormente, es natural que haya una gran cantidad de propiedades que se hereden del límite de sucesiones. A continuación revisaremos algunas de ellas y podremos aprovechar la relación de ambos conceptos para hacer la demostración de las mismas.

Teorema. Sean $f: A \rightarrow \mathbb{R}$ y $g: A \rightarrow \mathbb{R}$ dos funciones y sea $c \in \mathbb{R}$. Si $$\lim_{x \to x_0} f(x) = L \quad \text{ y } \quad \lim_{x \to x_0} g(x) = M.$$
Entonces

  1. $$\lim_{x \to x_0} c \cdot f(x) = cL.$$
  2. $$\lim_{x \to x_0} (f+g)(x) = L+M.$$
  3. $$\lim_{x \to x_0} (f-g)(x) = L-M.$$
  4. $$\lim_{x \to x_0} (f \cdot g)(x) = L\cdot M.$$
  5. Si además $M \neq 0$, entonces $$\lim_{x \to x_0} \left( \frac{f}{g} \right) (x) = \frac{L}{M}.$$

Demostración

Daremos la demostración del inciso 4 y la demostración de los demás es análoga.

Sea $\{ a_n \}$ una sucesión en $A$ que converge a $x_0$ tal que $a_n \neq x_0$ para todo $n\in \mathbb{N}$, por el teorema anterior tenemos que
$$\lim_{n \to \infty} f(a_n) = L \quad \text{ y } \quad \lim_{n \to \infty} g(a_n) = M.$$

De esta forma podemos usar las propiedades de convergencia de una sucesión, así

$$\lim_{n \to \infty} (f \cdot g)(a_n) = \lim_{n \to \infty} \left( f(a_n) \cdot g(a_n) \right) = \lim_{n \to \infty} f(a_n) \cdot \lim_{n \to \infty} g(a_n) = L \cdot M.$$
Por el teorema revisado, podemos concluir que $$\lim_{x \to x_0} (f \cdot g)(x) = L \cdot M.$$

$\square$

Observación. Particularmente podemos generalizar los puntos 2 y 4, de tal forma que si $f_1, f_2, \dots, f_n$ son funciones definidas de $A$ a $\mathbb{R}$ cada una con límite $L_1, L_2, \dots L_n$ en $x_0$. Entonces

\begin{gather*}
\lim_{x \to x_0} (f_1 + f_2 + \ldots + f_n) (x) = L_1 + L_2 + \ldots + L_n \\
\text{ y } \\
\lim_{x \to x_0} (f_1 \cdot f_2 \cdot \ldots \cdot f_n)(x) = L_1 \cdot L_2 \cdot \ldots \cdot L_n.
\end{gather*}

Revisaremos un par de ejemplos donde aplicaremos las propiedades anteriores.

Ejemplo 1. Calcula $$\lim_{x \to 2} \frac{5x-12}{2x + 10}.$$
\begin{align*}
\lim_{x \to 2} \frac{5x-12}{2x + 10} =& \frac{ \lim_\limits{x \to 2} ( 5x-12 ) }{ \lim_\limits{x \to 2} (2x + 10) } \text{, por el punto 5 del teorema anterior} \\ \\
= & \frac{ \lim_\limits{x \to 2} 5x – \lim_\limits{x \to 2} 12 }{ \lim_\limits{x \to 2} 2x + \lim_\limits{x \to 2} 10 } \text{, por los puntos 2 y 3 del teorema anterior} \\ \\
= & \frac{10-12}{4+10} \\ \\
= & – \frac{1}{7}.
\end{align*}
$$\therefore \lim_{x \to 2} \frac{5x-12}{2x + 10} = – \frac{1}{7}.$$

Ejemplo 2. Calcula $$\lim_{x \to 5} \frac{x^3+3}{8x^2 + 7}.$$
\begin{align*}
\lim_{x \to 5} \frac{x^3+3}{8x^2 + 7} = & \frac{\lim_\limits{x \to 5} (x^3+3)}{ \lim_\limits{x \to 5} (8x^2 + 7)} \text{, por el punto 5 del teorema anterior} \\ \\
= & \frac{\lim_\limits{x \to 5} x^3+ \lim_\limits{x \to 5} 3}{ \lim_\limits{x \to 5} 8x^2 + \lim_\limits{x \to 5} 7} \text{, por el punto 2 del teorema anterior} \\ \\
= & \frac{125+ 3}{200 + 7} \\ \\
= & \frac{128}{207}.
\end{align*}
$$\therefore \lim_{x \to 5} \frac{x^3+3}{8x^2 + 7} = \frac{128}{207}.$$

En los ejemplos anteriores se hizo énfasis en las propiedades que nos permitieron calcular el límite con la finalidad de mostrar claramente cómo se emplean, sin embargo, esto no será necesario y, de hecho, no se hará tal hincapié de ahora en adelante.

A continuación probaremos el teorema del sándwich para el límite de una función.

Teorema. Sean $f$, $g$, $h : A \rightarrow \mathbb{R}$ y sea $x_0 \in A$. Si

$$f(x) \leq g(x) \leq h(x) \text{, para todo } x \in A, x \neq x_0,$$

y si $$\lim_{x \to x_0} f(x) = L \quad \text{ y } \quad \lim_{x \to x_0} h(x) = L.$$

Entonces

$$\lim_{x \to x_0} g(x) = L.$$
Demostración

Sea $\varepsilon > 0 $, como $f$ y $h$ tienen como límite a $L$ en $x_0$, entonces existen $\delta_1$, $\delta_2$ tales que

\begin{gather*}
0<|x-x_0|< \delta_1, \quad \text{entonces} \quad |f(x)-L|< \varepsilon \\
\text{ y } \\
0<|x-x_0|< \delta_2, \quad \text{entonces} \quad |h(x)-L| < \varepsilon.
\end{gather*}

Consideremos $\delta = min\{ \delta_1, \delta_2 \}$, si $0<|x-x_0|< \delta$, se cumple que

\begin{gather*}
-\varepsilon < f(x)-L < \varepsilon \quad \Leftrightarrow \quad L-\varepsilon < f(x) < L + \varepsilon \\
\text{ y } \\
-\varepsilon < h(x)-L < \varepsilon \quad \Leftrightarrow \quad L-\varepsilon < h(x) < L + \varepsilon.
\end{gather*}

Además, por hipótesis se tiene que $f(x) \leq g(x) \leq h(x)$, entonces

\begin{gather*}
L-\varepsilon < f(x) \leq g(x) \quad \text{ y } \quad g(x) \leq h(x) < L + \varepsilon.
\end{gather*}
Se sigue que
\begin{gather*}
L-\varepsilon < g(x) < L + \varepsilon. \\ \\
\Leftrightarrow -\varepsilon < g(x) – L< \varepsilon. \\ \\
\therefore |g(x) – L| < \varepsilon. \\ \\
\therefore \lim_{x \to x_0} g(x) = L.
\end{gather*}

$\square$

A continuación veremos un ejemplo donde podemos aplicar el teorema del sándwich.

Ejemplo 3. Encuentra el siguiente límite: $$\lim_{x_0 \to 0} x^2 e^{sen(\frac{1}{x})}.$$
Sabemos que

\begin{gather*}
– 1 \leq sen(\frac{1}{x}) \leq 1 \text{, para todo } x \neq 0.
\end{gather*}
Dado que la función exponencial no altera la relación de orden, entonces tenemos
\begin{gather*}
e^{- 1} \leq e^{sen(\frac{1}{x})} \leq e^{ 1}.
\end{gather*}
Se sigue que
\begin{gather*}
x^2 e^{- 1} \leq x^2 e^{sen(\frac{1}{x})} \leq x^2 e^{ 1}.
\end{gather*}

La función original $g(x) = x^2 e^{sen(\frac{1}{x})}$ está acotada por $f(x) = x^2 e^{- 1}$ y $h(x) = x^2 e^{1}$. Tal como se muestra en la siguiente gráfica:

Notemos que
$$\lim_{x \to 0} x^2 e^{- 1} = 0 \quad \text{ y } \quad \lim_{x \to 0} x^2 e^{1} = 0.$$
Por el teorema del sándwich podemos concluir que $$\lim_{x_0 \to 0} x^2 e^{sen(\frac{1}{x})} = 0.$$

En esta entrada revisamos algunas de las propiedades que tiene el límite de una función haciendo uso del límite de sucesiones, pero vale la pena destacar que también se pudo recorrer este tramo del camino usando la definición épsilon-delta y te invitamos a realizar el ejercicio de demostrar algunas de las propiedades haciendo uso de tal definición con la finalidad de tener un dominio mayor del concepto.

Más adelante…

Extenderemos la noción de límite de una función definiendo una nueva clase de límites: los límites laterales. Veremos la definición de límite por la derecha y límite por la izquierda que son definiciones menos exigentes y las cuales nos permiten tener un análisis más detallado para aquellas funciones donde el límite no existe.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  • Prueba que si $$\lim_{x \to x_0} f(x) = L \text{, entonces } \lim_{x \to x_0} |f(x)| = |L|.$$
  • Calcula el límite $$\lim_{x \to 0} \frac{(x+1)^2-1}{x}.$$
  • Calcula el límite $$\lim_{x \to 0} \frac{\sqrt{x}-1}{x-1}.$$
  • Calcula el límite $$\lim_{x \to 0} x^2 cos \left( \frac{1}{x^2} \right).$$

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Cálculo Diferencial e Integral I: Definición formal de límite de una función

Por Juan Manuel Naranjo Jurado

Deja un comentario

Introducción

Anteriormente revisamos una definición intuitiva del límite con la finalidad de facilitar la comprensión de la definición formal. En esta entrada se dará la definición formal, así como algunos ejemplos para que el concepto sea comprendido en su totalidad.

Definición formal de límite

Retomemos la idea intuitiva a la que llegamos al final de la entrada anterior: logramos que $f$ se aproxime arbitrariamente, $\varepsilon$, a $L$ siempre que logremos que $x$ esté lo suficientemente cerca, $\delta$, de $x_0$ sin ser $x_0.$

Observación. Notemos que la última parte la podemos expresar como $0<|x-x_0|< \delta$, pues al pedir que la distancia entre $x$ y $x_0$ sea mayor que $0$ se captura la idea de que $x \neq x_0$.

Es importante resaltar que estamos dando por hecho que se puede evaluar la función $f$ en valores de $x$ cercanos a $x_0$. Es por ello que se presenta la siguiente definición.

Definición. Sea $ A \subset \mathbb{R}$. Un punto $x_0 \in \mathbb{R}$ es un punto de acumulación de $A$ si para todo $\delta > 0$ existe al menos un punto $x \in A$, $x \neq x_0$, tal que $|x-x_0| < \delta$.

Dada la definición anterior, si consideramos una función $f: A \to \mathbb{R}$, para calcular el límite, y asegurar que podemos evaluar $f$ en valores $x$ cercanos a $x_0$, deberemos pedir que $x_0$ sea punto de acumulación del dominio de la función, $A$. Con esto, tenemos todos los elementos para dar la definición de límite.

Definición. Sean $A \subset \mathbb{R}$ y $x_0$ un punto de acumulación de $A$. Para una función $f: A \to \mathbb{R}$, decimos que $L$ es el límite de $f$ en $x_0$ si para todo $\varepsilon > 0$ existe algún $\delta > 0$ tal que, para todo $x \in A$, si $0<|x-x_0|< \delta$, entonces $|f(x)-L|< \varepsilon.$

A continuación tenemos una imagen que nos permitirá visualizar la definición:

En la imagen podemos ver que si definimos un valor arbitrario $\varepsilon >0$, entonces lo que buscamos es un valor positivo $\delta$, tal que si $x$ está a una distancia menor que $\delta$ con respecto a $x_0$, entonces eso implique que $f(x)$ esté a una distancia menor que $\varepsilon$ con respecto a $L.$


A continuación revisaremos un ejemplo sencillo aplicando la definición.

Ejemplo 1. Demuestra que $$\lim_{x \to -1} \frac{x^2-5x-6}{x+1} = -7.$$

Demostración.
Sea $\varepsilon >0$. Notemos que si $x \neq -1$, entonces

\begin{align*}
\left\lvert \frac{x^2-5x-6}{x+1} – (-7) \right\rvert & = \left\lvert \frac{x^2-5x-6}{x+1} +7 \right\rvert \\ \\
& = \left\lvert \frac{x^2-5x-6+7x+7}{x+1} \right\rvert \\ \\
& = \left\lvert \frac{x^2+2x+1}{x+1} \right\rvert \\ \\
& = \left\lvert \frac{(x+1)^2}{x+1} \right\rvert \\ \\
& = \left\lvert x+1 \right\rvert.
\end{align*}
Tomemos entonces $\delta = \varepsilon$. Si $0<|x- (-1) | = |x+1 |< \delta$, entonces
$$\left\lvert \frac{x^2-5x-6}{x+1} – (-7) \right\rvert = \left\lvert x+1 \right\rvert < \delta = \varepsilon.$$
$$\therefore \left\lvert \frac{x^2-5x-6}{x+1} – (-7) \right\rvert < \varepsilon.$$
$$\therefore \lim_{x \to -1} \frac{x^2-5x-6}{x+1} = -7.$$

$\square$

Hagamos algunos comentarios respecto a la demostración. Como primer paso, establecimos un valor arbitrario positivo para $\varepsilon$. Después hicimos algunas manipulaciones algebraicas que nos permitieron simplificar la expresión original en una más simple con la cual logramos encontrar el valor de $\delta$ que sería útil, en este caso, ese valor fue justamente el mismo que $\varepsilon$.

Revisemos un segundo ejemplo.

Ejemplo 2. Sea $f(x) = \frac{3x+1}{2x}$, entonces $$\lim_{x \to 2} f(x) = \frac{7}{4}.$$

Demostración.

Sea $\varepsilon > 0$. Veamos que

\begin{align*}
\left\lvert f(x) – \frac{7}{4}\right\rvert & = \left\lvert \frac{3x+1}{2x} – \frac{7}{4} \right\rvert \\ \\
& = \left\lvert \frac{6x+2-7x}{4x} \right\rvert \\ \\
& = \left\lvert \frac{2-x}{4x} \right\rvert \\ \\
& = \frac{|2-x|}{|4x|} \\ \\
& = \frac{|x-2|}{|4x|} \\ \\
& = \frac{1}{|4x|} \cdot |x-2|.
\end{align*}

De lo anterior, se sigue que
\begin{align*}
\left\lvert f(x) – \frac{7}{4}\right\rvert = \frac{1}{|4x|} \cdot |x-2|. \tag{1}
\end{align*}

Buscamos entonces acotar la expresión $(1)$, para ello podemos ver lo siguiente, si $|x-2| < 1$, entonces

\begin{gather*}
& |2|-|x| \leq |x-2| < 1.
\end{gather*}

De lo anterior, se sigue que

\begin{gather*}
& |2|-|x| < 1. \\
\Leftrightarrow & 2-1 < |x|. \\
\Leftrightarrow & 1 < |x|. \\
\Leftrightarrow & 1 >\frac{1}{|x|}. \\
\Leftrightarrow & \frac{1}{4} >\frac{1}{4|x|} = \frac{1}{|4x|}. \\
\end{gather*}

Por tanto, se tiene que

\begin{align*}
\frac{1}{|4x|} < \frac{1}{4}. \tag{2}
\end{align*}

Entonces si $|x-2| < 1$, por (1) y (2), tenemos lo siguiente
\begin{align*}
\left\lvert f(x) – \frac{7}{4}\right\rvert & = \frac{1}{|4x|} \cdot |x-2| \\ \\
& < \frac{1}{4} \cdot |x-2|.\\
\end{align*}

Previamente acotamos $|x-2|$ por el valor $1$, pero de la última expresión se sigue que deberemos acotarlo también por $4 \varepsilon$ para llegar a nuestro objetivo, tomemos así $\delta = min\{1, 4 \varepsilon\}.$


Si $0<|x- 2| \leq \delta$. Es decir, si $|x- 2| \leq 1$ y $|x- 2| \leq 4\varepsilon$, entonces
$$\left\lvert f(x) – \frac{7}{4}\right\rvert < \frac{1}{4} |x-2| \leq \frac{1}{4} \cdot 4\varepsilon.$$
$$ \therefore \left\lvert f(x) – \frac{7}{4}\right\rvert < \varepsilon.$$

$\square$

Nuevamente haremos énfasis en los pasos generales de la demostración. Iniciamos dando un valor de $\varepsilon$ arbitrario, y la tarea es encontrar el valor $\delta >0$ que acote la distancia entre $x$ y $x_0 = 2$ de tal manera que los valores de la función $f$ se aproximen a $L$ lo suficiente para que su distancia sea menor que $\varepsilon.$

Trabajemos ahora sobre el siguiente ejemplo.

Ejemplo 3. Para todo $x_0 \in \mathbb{R}$ se tiene que $$\lim_{x \to x_0} x^2 = x_0^2.$$

Demostración.

Sea $\varepsilon > 0$ y $x_0 \in \mathbb{R}$. Notemos que

$|x^2 – x_0^2| = |x-x_0||x+x_0|.$

Haciendo uso de una manipulación análoga al del ejemplo anterior, podemos ver que si $|x-x_0| < 1$, entonces

$|x|-|x_0| \leq |x-x_0| < 1 \quad \Rightarrow \quad |x| < 1 + |x_0|.$

Cabe resaltar que en el ejemplo anterior usamos la propiedad $|x_0|-|x| \leq |x-x_0|$, ya que la intención es acotar al recíproco de $x$. En este caso, se emplea $|x|-|x_0| \leq |x-x_0|$, puesto que buscamos acotar directamente a $x$.

Además,
\begin{align*}
|x + x_0| & \leq |x|+ |x_0| \\
& < 1 + |x_0|+|x_0| \text{, pues} \quad |x| < 1 + |x_0| \\
& = 1 + 2|x_0|.
\end{align*}

Así, tenemos que $$ |x + x_0| < 1 + 2|x_0|.$$

En esta ocasión queremos que $|x-x_0| < 1$ y, por la última expresión, también queremos que $|x-x_0| <\frac{\varepsilon}{1+2|x_0|}$, definimos así $\delta = min \{ 1, \frac{\varepsilon}{1+2|x_0|} \}$. Si $0 < |x-x_0| < \delta$, entonces

\begin{align*}
|x^2-x_0^2| & = |x-x_0||x+x_0| \\ \\
& < |x-x_0|(1+2|x_0|) \\ \\
& < \delta (1+2|x_0|) \\ \\
& \leq \frac{\varepsilon}{1+2|x_0|} \cdot (1+2|x_0|)\\ \\
& = \varepsilon.
\end{align*}

Esto implica que
$$|x^2-x_0^2| < \varepsilon.$$
$$\therefore \lim_{x \to x_0} x^2 = x_0^2.$$

$\square$

Unicidad del límite de una función

Después de haber revisado estos ejemplos, la definición de límite de una función (también llamada definición épsilon-delta), estamos listos para revisar la primera propiedad del límite.

Proposición. El límite de una función en $x_0$ es único, es decir, si $f$ tiende a $L$ en $x_0$ y $f$ tiende a $L’$ en $x_0$, entonces $L = L’.$


Demostración.
Sea $\varepsilon > 0$. Como $f$ tiende a $L$ y $L’$ en $x_0$, entonces para $\frac{\varepsilon}{2} > 0$ existen $\delta_1  > 0$ y $\delta_2 > 0$ tales que

\begin{gather*}
\text{Si } 0<|x-x_0|<\delta_1 \quad \Rightarrow \quad |f(x)-L| < \frac{\varepsilon}{2}. \\
\text{Si } 0<|x-x_0|<\delta_2 \quad \Rightarrow \quad |f(x)-L’| < \frac{\varepsilon}{2}. \\
\end{gather*}

Consideremos ahora $\delta = min\{\delta_1, \delta_2 \}$. Entonces si $0<|x-x_0|<\delta$ y, por la desigualdad del triángulo, esto implica que

\begin{align*}
|L-L’| \leq & |L-f(x)|+|L’-f(x)| \\
< & \frac{\varepsilon}{2} + \frac{\varepsilon}{2} \\
= & \varepsilon.
\end{align*}

Se sigue que

$|L-L’| < \varepsilon.$


Como $\varepsilon$ es un valor arbitrario positivo, podemos concluir que $L-L’ = 0$, es decir, $L=L’.$

$\square$

Más adelante…

En la siguiente entrada revisaremos con detalle varias propiedades que tienen los límites para lo cual haremos uso de una bella relación existente entre el límite de una sucesión y el de una función. Una vez revisadas estas propiedades, el cálculo de los límites se hará considerablemente más simple.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

Usando la definición épsilon-delta, demuestra lo siguiente:

  • $$\lim_{x \to x_0} c = c.$$
  • $$\lim_{x \to x_0} x = x_0.$$
  • $$\lim_{x \to 5} x+11 = 16.$$
  • $$\lim_{x \to -2c} (2c-3x) = 8c.$$
  • $$\lim_{x \to 0} \frac{x^2}{|x|} = 0.$$

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Cálculo Diferencial e Integral I: Idea intuitiva de límite de una función

Por Juan Manuel Naranjo Jurado

2 respuestas

Introducción

La definición de límite de una función suele ser uno de los conceptos más retadores dentro del cálculo y es por ello que, antes de entrar a su análisis formal, queremos dar una introducción con la finalidad de desarrollar la intuición necesaria para lograr el entendimiento de esta definición.

Idea intuitiva de límite de una función

Consideremos la función $f: \mathbb{R} \to \mathbb{R}$ tal que $f(x) = 10x$.

En la gráfica de la función $f(x) = 10x$, podemos observar que si $x$ toma valores cercanos a $2$, entonces $f(x)$ se aproxima a $20$. ¿Pero qué tanto es posible aproximar los valores de la función $f(x)$ a $20$?

Por ejemplo, ¿podemos encontrar un valor de $x$ distinto de $2$ tal que $f(x)$ esté a una distancia de $20$ menor que $12$ , es decir, $|f(x) – 20| < 12$?

Consideremos $x = 1$. De esta forma, $f(1) = 10$ y $|f(1) – 20| = |10 – 20| = 10 < 12$.

¿Podemos encontrar un valor de $x$ distinto de $2$ tal que $f(x)$ esté a una distancia de $20$ menor que $1$, es decir, $|f(x) – 20| < 1$?

Si tomamos $x=1.99$, se tiene que $|f(1.99) – 20| = |19.9 – 20| = 0.1 < 1$.

Hasta este momento, se han encontrado valores puntuales de $x$ que permiten que $f(x)$ se aproxime a $20$. Sin embargo, existen más valores de $x$ que lo pueden cumplir. Retomando la última aproximación deseada, podemos ver que $x=2.02$ también cumple el propósito, pues $|f(2.02) – 20| = |20.2- 20| = 0.2 < 1$. En realidad, es posible hallar todo un intervalo que lo cumpla.

Para poder obtener dicho intervalo, procedemos estableciendo la desigualdad deseada

\begin{gather*}
& |f(x) – 20| < 1. \\ \\
\Leftrightarrow & |10x – 20|< 1. \\ \\
\Leftrightarrow & \frac{|10x – 20|}{10}< \frac{1}{10}. \\ \\
\Leftrightarrow & |x – 2| < \frac{1}{10}.
\end{gather*}

Lo anterior indica que para que $f(x)$ esté a una distancia de $20$ menor que $1$, entonces $x$ debe estar a una distancia de $2$ menor que $\frac{1}{10}$.

¿Podemos encontrar un valor de $x$ distinto de $2$ tal que $f(x)$ esté a una distancia de $20$ menor que $\varepsilon > 0$, es decir, $|f(x) – 20| < \varepsilon$?

Análogamente, se obtiene que para que $|f(x)-20| < \varepsilon$, entonces $|x-2| < \frac{\varepsilon}{10}$. Generalizando más, podemos notar que para cualquier $x_0 \in \mathbb{R}$ se tiene que $|f(x)-10x_0| < \varepsilon$ con $x \neq x_0$, siempre que $|x-x_0| < \frac{\varepsilon}{10}.$

En la siguiente entrada se proporcionará la definición formal del límite. Sin embargo, de forma provisional para esta entrada, diremos que $L \in \mathbb{R}$ es el límite de la función $f$ en $x_0$ si la distancia entre $f(x)$ y $L$ es menor que un número $\varepsilon > 0$ elegido de antemano cuando $x$ se aproxima a $x_0$, pero es distinto de $x_0$.

Considerando lo anterior para nuestro ejemplo, se tiene que el límite de $f$ en $x_0 = 2$ es $L = 20$.

Usemos como segundo ejemplo la función $f: \mathbb{R} \to \mathbb{R}$ tal que $f(x) = x^2$.

Veremos que el límite de $f$ en $x_0 = 4$ es $L=16$. Para ello, notemos que

\begin{gather*}
& |f(x) – 16| < \varepsilon. \\
\Leftrightarrow & |x^2 – 16| < \varepsilon. \\
\Leftrightarrow & |(x-4)(x+4)| < \varepsilon. \\
\Leftrightarrow &|x-4||x+4| < \varepsilon.
\end{gather*}

A diferencia del caso anterior, parece que no es tan directo llegar a nuestro objetivo, pero notemos que particularmente podemos pedir que $|x-4| < 1$, entonces

\begin{gather*}
& -1< x-4 < 1. \\
\Leftrightarrow & 3 < x < 5. \\
\Leftrightarrow & 7 < x+4<9.
\end{gather*}

En resumen, si $|x-4|<1$, entonces $|x+4| < 9$. Lo cual implica que
$$|x^2 – 16| = |x-4||x+4| < 9|x-4|.$$
Si además restringimos la distancia de $x$ respecto a $4$ de tal manera que $|x-4| < \frac{\varepsilon}{9}$ y retomando la expresión anterior llegamos a lo siguiente:

\begin{gather*}
|x^2 – 16| = |x-4||x+4| < 9|x-4| < 9 \cdot \frac{\varepsilon}{9} = \varepsilon. \\
\therefore |x^2 – 16| < \varepsilon.
\end{gather*}

Esto siempre que $|x-4|$ sea menor que $1$ y $\frac{\varepsilon}{9}$, es decir, siempre que $|x-4| < min\{1, \frac{\varepsilon}{9} \}$.


De los dos ejemplos revisados en esta entrada, podemos notar que logramos que $f(x)$ se aproxime a $L$ con una distancia menor de épsilon cuando $x$ está lo suficientemente cerca de $x_0$. Para lograr esto último, acotamos $x-x_0$ en términos de un valor positivo que depende de $\varepsilon$ (para el primer ejemplo fue $\frac{\varepsilon}{5}$ y para el segundo $min\{1, \frac{\varepsilon}{9} \}$). Vale la pena entonces darle un nombre a este valor positivo: $\delta$.

Parafraseando: Logramos que $f$ se aproxime arbitrariamente, dado $\varepsilon > 0$, a $L$ cuando $x$ está lo suficientemente cerca, $\delta > 0$, de $x_0$.

Obtenemos así un indicio muy importante, para probar que $L$ es el límite de $f$ en $x_0$, habrá que dar un valor arbitrario fijo y positivo $\varepsilon > 0$ para el cual necesitaremos encontrar otro valor positivo, $\delta > 0$, tal que si $|x-x_0|<\delta$, entonces se cumpla que $|f(x)-L| < \varepsilon$. Adicionalmente, se pide que $x \neq x_0$, tal condición puede ser compactada de la siguiente forma $0 < |x-x_0| < \delta$, pues que la distancia entre $x$ y $x_0$ sea mayor que cero implica directamente que son distintos.

Antes de finalizar con esta entrada, es conveniente aclarar que no siempre tendremos funciones tan amigables en las cuales podamos evaluar directamente el valor de $x_0$ en $f$ para encontrar $L$. Incluso habrá ocasiones en las cuales no nos podamos aproximar de la manera en la que lo hicimos en estos ejemplos, pero por ahora no daremos muchos detalles extra al respecto, será tema para entradas posteriores.

Más adelante…

En la siguiente entrada daremos la definición formal de límite de una función y veremos varios ejemplos de funciones cuyo límite existe. Una vez dominemos la definición podremos incursionar en varias de sus propiedades y podremos tomar ventaja de estos conocimientos para tener una mayor comprensión sobre el comportamiento de diversas funciones de interés.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

Para corroborar que la idea intuitiva de límite de una función se ha comprendido, se queda como ejercicio realizar un análisis similar al expuesto en esta entrada. Consideremos la función $f(x) = 4x^2$ definida para todo $x \in \mathbb{R}$. En este caso, tomaremos $x_0=3$ y $f(x_0) = 4(3)^2 =36.$

  • Grafica $f(x)$.
  • Encuentra un valor de $x$ tal que $|f(x)-36| < 30$.
  • Encuentra un valor de $x$ tal que $|f(x)-36| < 1$.
  • Encuentra un intervalo de $x$ alrededor de $x_0 = 3$ tal que $|f(x)-36| < \frac{1}{100}$.
  • Encuentra un intervalo de $x$ alrededor de $x_0 = 3$ tal que $|f(x)-36| < \varepsilon$, con $\varepsilon > 0$.

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»