Archivo de la etiqueta: índice de H en G

Álgebra Moderna I: Teoremas de Sylow

Por Cecilia del Carmen Villatoro Ramos

Deja un comentario

(Trabajo de titulación asesorado por la Dra. Diana Avella Alaminos)

Introducción

En la entrada anterior definimos a los $p$-subgrupos de Sylow de un grupo $G$ como un $p$-subgrupo de $G$ tal que no estuviera contenido en otro $p$-subgrupo de $G$. En esta entrada estudiaremos los Teoremas de Sylow que hablan, como su nombre nos indica, de los $p$-subgrupos de Sylow que definimos antes.

El primero trata sobre del orden de los $p$-subgrupos de Sylow, que es la máxima potencia de $p$ que divide al orden del grupo $G$. El segundo habla de la relación entre los $p$-subgrupos de Sylow y establece que todo par de $p$-subgrupos son conjugados. El tercero describe de modo aproximado la cantidad de $p$-subgrupos de Sylow que hay en un grupo $G$. No nos da un número exacto, pero nos da alguna información al respecto.

Ahora, prepárate para leer el nombre de Sylow aún más veces.

Primer Teorema de Sylow

Teorema (1er Teorema de Sylow). Sea $p\in\z^+$ un primo, $G$ un grupo finito con $|G|=p^t m$, $t\in\n^+, m\in \n^+, p\not{|}m.$ Entonces

  1. para cada $i\in\{1,\cdots,t\}$, $G$ contiene un subgrupo de orden $p^i$.
  2. Todo subgrupo de $G$ de orden $p^i$ con $i\in\{1,\cdots,t-1\}$ es un subgrupo normal de algún subgrupo de $G$ de orden $p^{i+1}$.

Demostración.
Sea $p\in\z^+$ un primo, $G$ un grupo finito con $|G|=p^tm$, $t,m\in \n^+$, $p\not{|}m$.

P.D. Para toda $i\in\{1,\cdots,t\}$ existe $P_i \leq G$ con $|P_i| = p^{i}$ y de forma que $P_i \unlhd P_{i+1}$ para toda $i\in\{1,\cdots,t-1\}$.
De hecho, con esto quedarían probados los dos incisos del PTS (Primer Teorema de Syow).

Primero necesitamos un subgrupo de orden $p$. Éste se tiene gracias al Teorema de Cauchy. Así, podemos afirmar que $G$ tiene un subgrupo de orden $p$.
Ahora, si $i\in\{1,\cdots, t-1\}$ y $H$ es un subgrupo de orden $p^{i}$ veamos que podemos construir un subgrupo de $G$ de orden $p^{i+1}$ tal que $H$ sea normal a él:

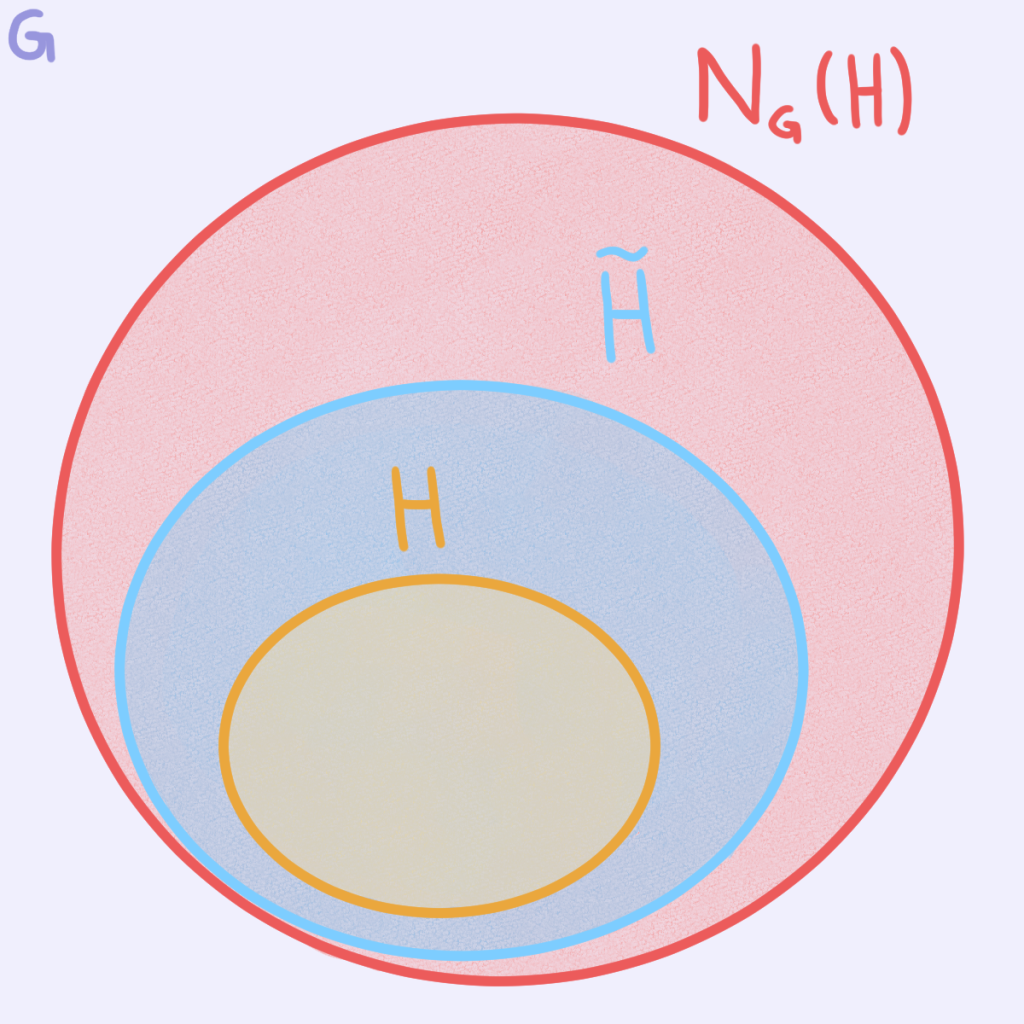
Sabemos que $p$ divide a $ [ G : H ]$ y como $[ G : H ] \equiv [ N_G(H) : H ] (\text{mód } p)$ entonces
\begin{align*}
p\text{ divide a } [ N_G(H) : H ] = \left| N_G(H) \Big{/}H \right|.
\end{align*}

Entonces por Cauchy, el grupo cociente $N_G(H)\Big{/}H$ tiene un subgrupo de orden $p$, y por el teorema de la correspondencia es de la forma $\tilde{H}/H$ con $H\leq \tilde{H} \leq N_G(H)$. Así,

\begin{align*}
&p = \left| \tilde{H} \Big/ H \right| = \frac{|\tilde{H}|}{|H|} = \frac{\tilde{H}}{p^{i}}
\\& \Rightarrow \frac{|\tilde{H}|}{p^{i}} = p
\\&\Rightarrow |\tilde{H}| = p^{i+1}
\end{align*}
pero $H\unlhd N_G(H)$ por construcción del normalizador y $ \tilde{H} \leq N_G(H)$, entonces $H \unlhd \tilde{H}.$

Ilustración de por qué $H\unlhd \tilde{H}$.

De esta manera, dado un subgrupo de orden $p^i$ podemos encontrar un subgrupo de orden $p^{i+1}$ tal que el primero sea normal en el segundo. Entonces, considerando $P_1$ un subgrupo de $G$ de orden $p$, existe $P_2$ un subgrupo de $G$ de orden $p^2$ tal que $P_1\unlhd P_2$ y a partir de $P_2$ podemos hallar $P_3$ un subgrupo de $G$ de orden $p^3$ tal que $P_2\unlhd P_3$ y así sucesivamente.

Concluimos entonces que existen $P_1,\cdots, P_t$ subgrupos de $G$ con $|P_i| = p^{i}$ para toda $i\in \{1,\cdots, t\}$ tales que $P_1 \unlhd P_2 \unlhd \cdots \unlhd P_t$.

$\blacksquare$

En consecuencia, el PTS nos dice qué tamaño tienen los $p$-subgrupos de Sylow, una incógnita que no habíamos resuelto. Esto se ilustra en el siguiente corolario.

Corolario. Sea $p\in\z^+$ un primo, $G$ un grupo finito con $|G| = p^tm$, $t,m,\in \n^+$ y $p\not{|}m$. Los $p$-subgrupos de Sylow de $G$ tienen orden $p^t$.

Segundo Teorema de Sylow

Antes de enunciar y probar el STS (Segundo Teorema de Sylow) vamos a dar una observación.

Observación. Los conjugados de un $p$-subgrupo de Sylow son también $p$-subgrupos de Sylow.

Demostración.
Sea $p\in\z^+$ un primo, $G$ un grupo finito, $|G| = p^tm$ con $t,m\in\n^+$, $p\not{|}m.$

Al tomar $P$ un $p$-subgrupo de Sylow de $G$, por el corolario del PTS sabemos que $|P| = p^t$.

Ahora, al conjugarlo mediante $g\in G$ se tiene que $gPg^{-1} \leq G$ con $|gPg^{-1}| = |P| = p^t$. Así, $gPg^{-1}$ es un $p$-grupo y debido a que su orden es la máxima potencia de $p$ que divide a $|G|$ se tiene que es un $p$-subgrupo de Sylow.

$\blacksquare$

Esta observación nos dice que todos los conjugados de un $p$-subgrupo de Sylow son igual un $p$-subgrupo de Sylow, pero el STS va más allá y nos dice que conjugando $p$-subgrupos de Sylow podemos encontrar todos los $p$-subgrupos de Sylow de un grupo $G$.

Teorema (2do Teorema de Sylow). Sean $p\in \z^+$ un primo, $G$ un grupo finito. Todos los $p$-subgrupos de Sylow de $G$ son conjugados en $G$.

Demostración.

Sea $p\in \z^+$ un primo, $G$ un grupo finito, $P$ y $Q \; p$-subgrupos de Sylow de $G$.

Sea $X = \{gP \;|\; g\in G\}$. Para comenzar definimos $q\cdot(gP) = qgP$ para todas $q\in Q,g\in G.$ Ésta es una acción de $Q$ en $X$. Como $Q$ es un $p$-grupo, por el último teorema de la entrada Clase de Conjugación, Centro de $G$, Ecuación de Clase y  $p$-Grupo sabemos que
\begin{align*}
\#X\equiv\#X_Q (\text{mód } p).
\end{align*}

Como $p$ no divide a $[ G: P ]$ y $[ G: P ] = \# X$, entonces $p$ tampoco divide a $\# X_Q$. En particular $\#X_Q \neq 0$ y así $X_Q \neq \emptyset$.

Pero
\begin{align*}
X_Q &= \{gP \;|\; q\cdot (gP) = gP \quad \forall q\in Q\}\\
&= \{gP \;|\; qgP = gP \quad \forall q\in Q\} \\
&= \{gP \;|\; g^{-1}qg \in P\quad \forall q\in Q\} \\
&= \{gP \;|\; g^{-1}Qg \subseteq P\} & \text{porque es para toda }q\in Q\\
&= \{gP \;|\; g^{-1}Qg = P\}.
\end{align*}

donde la última igualdad se da porque $g^{-1}Qg$ y $P$ son $p$-subgrupos de Sylow y entonces tienen el mismo orden, la máxima potencia de $p$ que divide al orden de $G$.

Así, $\{gP \;|\;g^{-1}Qg = P\}\neq \emptyset$ y en consecuencia existe $g\in G$ tal que $g^{-1}Qg = P$.

Por lo tanto $P$ y $Q$ son conjugados en $G$.

$\blacksquare$

Tercer Teorema de Sylow

Teorema (3er Teorema de Sylow). Sea $p\in \z^+$ un primo, $G$ un grupo finito y $r_p$ el número de $p$-subgrupos de Sylow de $G$. Entonces

  1. $r_p \equiv 1 (\text{mód } p)$.
  2. $r_p$ divide a $ |G|$.

Demostración.
Sea $p\in \z^+$ un primo, $G$ un grupo finito y $r_p$ el número de $p$-subgrupos de Sylow de $G$.

  1. Sea $X = \{P_1,\cdots, P_{r_p}\}$ la colección de todos los $p$-subgrupos de Sylow de $G$. Definimos $g\cdot P_i = gP_ig^{-1}$ para todas $g\in P_1$ e $i\in\{1,\cdots, r_p\}$, que es una acción de $P_1$ en $X$ ya que $ gP_ig^{-1}$ es nuevamente un $p$-subgrupo de Sylow por la observación previa. Como $P_1$ es un $p$-grupo, por el último teorema de la entrada Clase de Conjugación, Centro de $G$, Ecuación de Clase y  $p$-Grupo sabemos que
    \begin{align*}
    \#X \equiv \# X_{P_1} (\text{mód } p).
    \end{align*}
    Pero por la construcción de $X$, tenemos que $$r_p = \#X\equiv \# X_{P_1} (\text{mód } p).$$
    Ahora, veamos que $\#X_{P_1} = 1$ y para ello analicemos quién es $X_{P_1}$
    \begin{align*}
    X_{P_1} &= \{P_i \in X \;|\; g\cdot P_i = P_i \quad \forall g\in P_1\} \\
    &= \{P_i \in X \;|\; gP_ig^{-1}=P_i \quad \forall g\in P_1\}.
    \end{align*}
    Así, para toda $P_i \in X_{P_1}$ se tiene que $P_1 \leq N_G(P_i)$ y también $P_i \leq N_G(P_i)$.
    Entonces $P_1$ y $P_i$ son $p$-subgrupos de Sylow de $N_G(P_i).$
    Por el 2do Teorema de Sylow, $P_1$ y $P_i$ son conjugados en $N_G(P_i)$, es decir existe $g\in N_G(P_i)$ tal que
    \begin{align*}
    P_1 &= gP_ig^{-1} \\
    &= P_i &\text{pues } g\in N_G(P_i).
    \end{align*}
    Concluimos entonces que $P_1$ es el único elemento en $X_{P_1}$ y así $\#X_{P_1} = 1$. Por lo tanto $r_p \equiv 1 (\text{mód } p)$.
  2. Sea $X = \{P_1, \cdots, P_{r_p}\}$ la colección de todos los $p$-subgrupos de Sylow de $G$.
    Definimos $g\cdot P_i = gP_ig^{-1}$ para todas $g\in G$ e $i\in\{1,\cdots, r_p\}$, que es una acción de $G$ en $X$.
    Por el segundo teorema de Sylow sabemos que $P_1,\dots , P_{r_p}$ son conjugados de $P_1$, entonces $$ \mathcal{O}(P_1)=\{g\cdot P_1|g\in g\}=\{gP_1g^{-1}|g\in g\}=\{P_1,\dots , P_{r_p}\}=X$$ es decir, la acción es transitiva.
    Entonces obtenemos que $r_p = \# \mathcal{O}(P_1)$. Pero, sabemos que $$\# \mathcal{O}(P_1) = [ G : G_{P_i} ] = \frac{|G|}{|G_{P_i}|}$$
    que es un divisor de $|G|$. Por lo tanto $r_p$ es un divisor de $ |G|$.

$\blacksquare$

Tarea moral

  1. Demuestra el corolario del PTS: Sea $p\in\z^+$ un primo, $G$ un grupo finito con $|G| = p^tm$ con $t,m,\in \n^+$ y $p\not{|}m$. Los $p$-subgrupos de Sylow de $G$ tienen orden $p^t$.
  2. Sean $p\in \z^+$ un número primo, $G$ un grupo y $P$ un $p$-subgrupo de Sylow de $G$. Demuestra que $P$ es el único $p$-subgrupo de Sylow de $G$ si y sólo si $P \unlhd G.$
  3. Sea $p\in \z^+$ un número primo. Da un ejemplo de un grupo finito $G$ que tenga tres $p$-subgrupos de Sylow $P$, $Q$ y $R$ tales que $P\cap Q = \{1\}$ y $P\cap R \neq \{1\}.$
    (Sugerencia: Considera $S_3\times S_3.$)
  4. Sean $p\in \z^+$ un número primo y $G$ un grupo finito. Considera $Q$ un $p$-subgrupo de $G$ tal que $Q \unlhd G$. Prueba que $Q \leq P$ para cada $p$-sugrupo de Sylow $P$ de $G$.
    (Sugerencia: Usa el hecho de que cualquier otro $p$-subgrupo de Sylow de $G$ es conjugado de $P$.)
  5. Sean $p\in \z^+$ un número primo y $G$ un grupo finito. Para cada primo $p$ divisor del orden de un grupo finito $G$, escoge un $p$-subgrupo de Sylow $Q_p$. Prueba que $$G = \left< \bigcup_p Q_p\right>.$$(Sugerencia: Usa el orden de los subgrupos generados por los subgrupos de Sylow.)

Más adelante…

En esta entrada abarcamos los tres Teoremas de Sylow, se colocaron los tres en esta entrada para que fuera más fácil consultarlos. Sin embargo, esto hace a la entrada un poco larga, así que la siguiente estará dedicada a algunos ejemplos de la aplicación de estos teoremas.

Entradas relacionadas

Álgebra Moderna I: Teorema de Lagrange

Por Cecilia del Carmen Villatoro Ramos

2 respuestas

(Trabajo de titulación asesorado por la Dra. Diana Avella Alaminos)

Introducción

En la entrada anterior vimos que si tenemos un grupo $G$ y nos agarramos un subgrupo $H$, obtenemos una partición $H, a_1H, a_2H, a_3H, \dots, a_tH$ donde
\begin{align*}
|H| = \#a_2 H = \#a_3 H = \cdots = a_t H.
\end{align*}

Recuerda que $|G|$ se refiere al orden de un grupo y $\#a_iH$ es el orden de un conjunto que no es necesariamente un grupo. Esto quiere decir que el orden de $G$ es un $t$ veces del orden de $H$, en decir $|G| = t|H|.$ Este resultado sencillo pero importante es conocido como el Teorema de Lagrange, aunque en esta entrada, lo definimos en términos del índice de $H$ en $G$, $[G:H]$.

Joseph-Louis Lagrange, conocido simplemente como Lagrange, nació en 1739 y falleció en 1813.

Ejemplo de la partición $\{H, a_1H,\dots, a_tH\}$.

A pesar de que vivió antes de que la teoría de conjuntos se desarrollara en el siglo XIX, su trabajo fue muy importante para ella. Por eso este teorema tiene su nombre.

Ingredientes para la demostración

Lema. Sea $G$ un grupo, $H$ un subgrupo de $G$, $a\in G$. Entonces $$\# aH = |H|.$$

Demostración. Sean $G$ un grupo, $H\leq G$ y $a \in G$.

Consideremos $\varphi : H \to a \, H$, tal que $h \mapsto ah$.

Veamos que $\varphi$ es inyectiva ya que si tomamos $h, \bar{h} \in H$ son tales que $\varphi(h) = \varphi(\bar{h})$ entonces $ah = a \varphi$ y por cancelación, $h = (\bar h)$.

Además, $\varphi$ es suprayectiva ya que dado $ah \in aH$ con $h\in H$ tenemos
$$ ah = \varphi(h) \in \text{Im}\varphi. $$

Donde $\text{Im}\varphi$ es la imagen de $\varphi$.

Por lo tanto $|H| = \# a H$.

$\blacksquare$

Señoras y señores, les presento a Lagrange

Ahora ya tenemos todos los ingredientes para demostrar el teorema de Lagrange.

Teorema. (Teorema de Lagrange) Sea $G$ un grupo finito, $H$ subgrupo de $G$. Entonces $|H|$ divide al orden de $G$ y
$$[ G:H ] = \frac{|G|}{|H|}.$$

Demostración. Sea $G$ un grupo finito, $H\leq G$. Como $G$ es finito debe haber una cantidad finita de clases laterales izquierdas de $G$ en $G$, notemos que cada una es no vacía con al menos un elemento.

Sean $a_1, \dots , a_t \in G$ representantes de las distintas clases laterales izquierdas de $H$ en $G$, con $t = [ G : H ]$. Sabemos que $\displaystyle G = \bigcup^{t}_{i=1} a_i H$. Como $a_iH \cap a_jH = \emptyset$ para $i\neq j$, con $i,j\in\{1,\dots, t\}$, entonces la unión, es una unión disjunta. Así podemos hacer,

\begin{align*}
|G| = \left| \bigcup^{t}_{i=1} a_i H\right| &= \sum^{t}_{i=1} \#a_iH \\
&= \sum^{t}_{i = 1} |H| &\text{Lema anterior} \\
&= t|H| = [ G:H ] |H|
\end{align*}

Así $|G| = [ G : H ] |H|$, enconces $|H|\Big| |G|$ y $\displaystyle [ G : H ] = \frac{|G|}{|H|}$.

$\blacksquare$

Consecuencias del teorema

Corolario 1. Sea $G$ un grupo finito, $a\in G$. Entonces $o(a) \Big| |G|$. Así $a^{|G|} = e$.

Demostración. Sea $G$ un grupo finito, $a\in G$. Consideremos $\left< a \right> \leq G$. Por el teorema de Lagrange:

$$ o(a) = |\left< a \right>|\Big| |G| \Rightarrow o(a)\Big| |G|.$$

Así $|G| = o(a)q$, para algún $q \in \z$,
$$a^{|G|} = a^{o(a)q} = \left( a^{o(a)}\right)^q = e^q = e.$$

$\blacksquare$

Corolario 2. Todo grupo finito de orden primo es cíclico.

Demostración. Sea $G$ un grupo finito, $|G| = p$ con $p$ primo.

Como $|G| > 1$ sea $a \in G \setminus \{e\}$. Por el corolario 1,
$$1 < o(a) \Big| |G| = p.$$

Entonces $o(a) = p$. Así $\left< a \right> = G$ y $G$ es cíclico.

$\blacksquare$

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

  1. Sea $G$ un grupo finito, $H$ y $K$ subgrupos de $G$ con $K\subseteq H$. En cada inciso (son los ejercicios 2 y 3 de la entrada anterior) justifica usando el teorema de Lagrange ¿cómo es $[G:K]$ en términos de $[G:H]$ y $[H_K]$?
    1. $G = Q$ los cuaternios, $H = \left<i\right>$ y $K = \{\pm 1\}$.
    2. $G = S_4$, $H = A_4$ y $K = \left<(1\;2\;3)\right>$.
  2. Encuentra todos los subgrupos del grupo de los cuaternios y de $\z_8$ ¿de qué orden son? ¿cuántos hay del mismo orden?
  3. Revisa el video de la Sorbona: Lagrange-Universidad de la Sorbona. Se puede poner poner subtítulos en español.

Más adelante…

El teorema de Lagrange es uno de los resultados más importantes del curso. Se usará multiples veces. Por lo pronto, en la siguiente entrada, revisitaremos los grupos cíclicos y usaremos el teorema de Lagrange para probar una caracterización de esos grupos.

Entradas relacionadas

Álgebra Moderna I: Relación de equivalencia dada por un subgrupo e índice de $H$ en $G$

Por Cecilia del Carmen Villatoro Ramos

Deja un comentario

(Trabajo de titulación asesorado por la Dra. Diana Avella Alaminos)

Introducción

Como pudiste darte cuenta por el título, en esta entrada definiremos una relación de equivalencia en un grupo. Permítenos dar una motivación usando un grupo que tal vez ya hayas estudiado en cursos anteriores como el de Álgebra Superior II.

Dicho grupo tan importante, es el de los enteros con la suma $(\z, +)$. Para $a,b\in \z$ es posible establecer una relación $\thicksim$ dentro de los enteros como sigue
\begin{align*}
a \thicksim b \Leftrightarrow b-a \text{ es múltiplo de } n.
\end{align*}
Esta relación de equivalencia induce una partición de $\z$, con exáctamente $n$ conjuntos. Donde cada conjunto es una de las clases módulo $n$. En esta entrada queremos introducir una relación parecida, pero generalizada a cualquier grupo.

Comencemos modificando este ejemplo un poco. Primero, llamemos $H$ al conjunto de todos los enteros múltiplos de $n$. Así nuestra relación quedaría, para $a,b\in \z$,
\begin{align*}
a \thicksim b \Leftrightarrow b-a \in H.
\end{align*}

Luego, notemos que a pesar de que la operación que usamos para definir el grupo es la suma usual, nuestra relación está definida usando la resta. En realidad, lo que está pasando es que estamos sumando $b$ con el inverso aditivo de $a$, es decir $-a$. Entonces $b -a = b + (-a)$. Además, $(\z,+)$ es un grupo abeliano, por lo que $b + (-a) \in H \Leftrightarrow (-a) + b \in H$. Para nuestra generalización usaremos el segundo caso.

Así, tenemos que comenzar agarrando un subgrupo cualquiera de $G$, es decir, nos tomamos $H\leq G.$ Entonces nuestra relación debe quedar, dados $a,b\in G$,
\begin{align*}
a \thicksim b \Leftrightarrow a^{-1}b\in H.
\end{align*}

Ya al tener esa relación y demostrar que es una relación de equivalencia, usaremos las propiedades de grupo para descubrir que las clases de equivalencia son las clases laterales vistas en la entrada anterior.

Relación Generalizada

Lo anterior queda formalizado en la siguiente definición.

Definición. Sea $G$ un grupo y $H$ un subgrupo de $G$. Definimos una relación en $G$ del siguiente modo: dados $a,b \in G$,

\begin{align*}
a \thicksim b \Leftrightarrow a^{-1}b \in H.
\end{align*}

Ahora, demostraremos que esa relación, así como la de la introducción, es una relación de equivalencia.

Observación. La definición anterior es una relación de equivalencia.

Demostración.
Sean $G$ un grupo y $H\leq G$.

Primero, tomamos $a \in G$.
También podemos tomar $a^{-1}$ . Así $a^{-1}a = e \in H$. Por lo tanto $a \thicksim a$ y nuestra relación es reflexiva.

Ahora tomamos $a,b \in G$. Si $a \thicksim b$, entonces $a^{-1} b\in H$.

\begin{align*}
\Rightarrow b^{-1}a = (a^{-1}b)^{-1} \in H \Rightarrow b \thicksim a
\end{align*}

Por lo que nuestra relación es simétrica.

Sean $a,b,c \in G$. Si $a \thicksim b$ y $b \thicksim c$, entonces $a^{-1}b \in H$ y $b^{-1}c \in H$, entonces usando la cerradura de $H$ y asociando de otra manera, obtenemos

\begin{align*}
a^{-1}c = (a^{-1}b)(b^{-1}c) \in H \Rightarrow a \thicksim c.
\end{align*}

Así, nuestra relación es transitiva.

Por lo tanto, nuestra relación es una relación de equivalencia.

$\square$

Nótese que para probar las tres propiedades de una relación de equivalencia (reflexividad, simetría y transitividad) usamos las tres condiciones de un subgrupo (la existencia del neutro, la cerradura de los inversos y la cerradura del producto).

A continuación, veamos cómo son las clases de equivalencia:
Sea $a \in H$.

\begin{align*}
\bar{a} &= \{b \in G | a \thicksim b\} = \{b \in G | a^{-1}b \in H\} \\
&= \{b \in G | a^{-1}b = h, h \in H\} = \{b \in G | b = ah, h \in H\} \\
&= \{ah | h \in H\} = a H.
\end{align*}

Ahora veremos algunas observaciones de lo anterior.

Observación. Sean $G$ un grupo, $H\leq G$ y $a,b\in G$, entonces
\begin{align*}
a H = bH & \Leftrightarrow a^{-1}b \in H.
\end{align*}

En particular,
\begin{align*}
H = bH & \Leftrightarrow b \in H
\end{align*}

Nota. Análogamente se puede trabajar con clases laterales derechas, i.e. ($Ha = Hb \Leftrightarrow ba^{-1}\in H$).

Como $\thicksim$ es una relación de equivalencia, esta induce una partición y, como sus clases de equivalencia son las clases laterales, tenemos el siguiente teorema.

Teorema. Sea $G$ un grupo, $H$ subgrupo de $G$.

  1. $aH \neq \emptyset \quad \forall a \in G$ .
  2. Si $a,b \in G$ son tales que $aH \cap bH \neq \emptyset$, entonces $aH = bH$.
  3. $\displaystyle \bigcup_{a\in G} aH = G$

Claramente el teorema anterior enuncia las características de una partición, por lo que no hay nada que probar.

Ejemplos

Ejemplo 1. Consideremos al grupo de los cuaternios $Q$ , tomemos el subgrupo $H = \left< i \right> = \{\pm 1 , \pm i\}$. Veamos qué sucede con sus clases laterales.
\begin{align*}
jH &= \{j(+1), j(-1), j(+i), j(-i)\}\\
&= \{j, -j, -k k\} \\
&= Hj.
\end{align*}

La última igualdad la puedes comprobar tú, multiplicando los mismos elementos por $j$, pero ahora del lado izquierdo.

Así, las clases laterales son:

  • Clases laterales izquierdas: $H, jH$.
  • Clases laterales derechas: $H, Hj$.

Ejemplo 2. Tomemos $S_3$ y $H = \{(1), (32)\}$.
Primero, veamos cómo se ven las clases laterales izquierdas.

Primero, tenemos la clase del neutro, es decir $(1) H = H$. Luego, tenemos que tomarnos un elemento de $S_3$ que no esté en $H$, digamos $(1\;2\;3)$, entonces,
\begin{align*}
(1\;2\;3)H &= \{(1\;2\;3)(1), (1\;2\;3)(3\;2)\}\\
&= \{(1\;2\;3), (1\;2)\}.
\end{align*}

Repetimos lo anterior, tomamos un elemento de $S_3$ que no esté $H$ y sea distinto al que ya nos tomamos para obtener una clase distinta. Esto nos da
\begin{align*}
(1\;3\;2)H &= \{(1\;3\;2)(1), (1\;3\;2)(3\;2)\} \\
& = \{(1\;3\;2)(1\;3)\}.\\
\end{align*}

Por lo que las clases laterales izquierdas son:
\begin{align*}
&(1)H = H\\
&(1\;2\;3)H = \{(1\;2\;3), (1\;2)\}\\
&(1\;3\;2)H = \{(1\;3\;2)(1\;3)\}.\\
\end{align*}

De la misma manera obtenemos las clases laterales derechas:
\begin{align*}
&H(1) = H \\
&H(1\;2\;3) = \{(1)(1\;2\;3), (3\;2)(1\;2\;3)\} = \{(1\;2\;3), (1\;3)\} \\
&H(1\;3\;2) = \{(1)(1\;3\;2), (3\;2)(1\;3\;2)\} = \{(1\;3\;2), (1\;2)\}.\\
\end{align*}

Este ejemplo nos permite ver que las clases laterales izquierdas y las clases laterales derechas no siempre coinciden.

Partición del ejemplo 1.
Partición de las clases laterales izquierdas del ejemplo 2.
Partición de las clases laterales derechas del ejemplo 2.

Número de elementos en las clases laterales

El último ejemplo nos dice que las clases laterales derechas e izquierdas no siempre coinciden, sin embargo probaremos que siempre hay la misma cantidad de ambas.

Teorema. Sea $G$ un grupo, $H$ un subgrupo de $G$. Entonces

\begin{align*}
\#\{a H | a \in G\} = \#\{Ha | a \in G\}.
\end{align*}

Demostración.

Sea $\psi: \{a H | a \in G\} \to \{Ha | a \in G\}$, definida como $\psi(aH) = Ha^{-1} \quad \forall a \in G$. Probaremos que esta función es biyectiva.

Pequeño paréntensis:

Antes de comenzar con la demostración, pongamos atención a la definición de $\psi$. En un inicio podríamos pensar ¿por qué no hacemos $\psi(aH) = Ha$? La respuesta es simple, porque esto no funcionaría. Definamos una nueva función para ejemplificar, sea $\phi: \{a H | a \in G\} \to \{Ha | a \in G\} $ tal que $\phi(aH ) = Ha$.

Tomemos $b\in G$ tal que $aH = bH$, para que $\phi$ esté bien definida, necesitaríamos que $\phi(aH) = \phi(bH)$, es decir $Ha = Hb$. Por la relación que definimos, esto implica que si $a^{-1}b \in H$, entonces $ba^{-1} \in H$, pero esto no necesariamente es cierto porque el grupo puede no ser abeliano. Lo que sí sabemos es que si $a^{-1}b\in H$, entonces $Ha^{-1}b = H$, y así $Ha^{-1} = Hb^{-1}$.

Por esto es que escogimos a $\psi$ de esa manera.

Termina paréntesis. Ahora sí comencemos con la demostración.

Sean $a,b \in G$,

\begin{align*}
aH = bH & \Leftrightarrow a^{-1}b \in H \\
&\Leftrightarrow Ha^{-1}b = H \\
& \Leftrightarrow Ha^{-1} = Hb ^{-1} \\
& \Leftrightarrow \psi (aH) = \psi (bH).
\end{align*}
Por tanto, $\psi$ está bien definida y es inyectiva.

Además, dada $Ha, a \in G$.

\begin{align*}
Ha = H(a^{–1})^{-1} = \psi(a^{-1} H)
\end{align*}

así $\psi$ es suprayectiva.

Por lo tanto $\# \{aH | a \in G\} = \# \{Ha|a\in G\}.$

$\square$

Ahora, ya sabemos que la cantidad de clases laterales izquierdas es la misma que la de clases laterales derechas. Entonces podemos nombrar esto como el índice.

Definición. Sea $G$ un grupo, $H$ un subgrupo de $G$. El índice de $H$ en $G$ es

\begin{align*}
[G:H ] = \# \{aH | a\in G\}.
\end{align*}

Ejemplos

Retomemos los ejemplos que ya hemos visto.

  1. Tomemos a $Q$ como los cuaternios, $H= \left< i \right> = \{\pm 1, \pm i\}$
    $[Q:H]= 2$.
  2. Ahora, tomemos $S_3$, $H = \{(1), (3 2)\}$. Como ya vimos,
    $[S_3:H]= 3$.
  3. Consideremos el grupo $(\z, +)$ y $H = \{6m | m \in \z\}$.
    Hay 6 clases laterales: $H, 1+H, 2+H, 3+H, 4+H, 5+H$. Que serían los múltiplos de $6$, $6+1$, $6+2$, $\dots$ respectivamente.
    Así, $[\z, H ]= 6$.

Tarea moral

  1. Analizando los ejemplos que tienes hasta ahora observa si existe alguna relación entre el orden de un grupo $G$, el orden del subgrupo $H$ y la cantidad de clases laterales de $H$ en $G$.
  2. Considera $\{\pm 1\} \leq \left< i \right> \leq Q$. Describe las clases laterales izquierdas de $\{\pm 1\}$ en $\left< i \right>$, las clases laterales izquierdas de $\left< i \right>$ en $Q$, y las clases laterales izquierdas de $\{\pm 1\}$ en $Q$. Encuentra $[Q: \{\pm 1\}]$, $[Q:\left< i \right>]$ y $[\left< i \right>: \{\pm 1\}]$.
  3. Considera $\left< (1\;2\;3) \right> \leq A_4 \leq S_4$. Describe las clases laterales izquierdas de $\left< (1\;2\;3) \right>$ en $A_4$, las clases laterales izquierdas de $A_4$ en $S_4$, y las clases laterales izquierdas de $\left< (1\;2\;3) \right>$ en $S_4$. Encuentra $[S_4:\left< (1\;2\;3) \right>]$, $[S_4: A_4]$ y $[A_4: \left< (1\;2\;3) \right>]$.
  4. Puedes checar el video de Mathologer.

Más adelante…

Ahora conoces el índice de $H$ en $G$. Recúerdalo para la siguiente entrada, porque intentaremos describir el orden de $G$ en términos del orden de $H$ y del índice. Sin hacer trampa, ¿cómo crees que se puede relacionar el orden de $G$ y el índice?

Entradas relacionadas