Introducción
En cursos de Cálculo en el bachillerato, posiblemente resolviste ejercicios en los cuales te solicitaban hallar los puntos críticos de una función y realizar la gráfica de la misma basándote en ellos.
Recordemos primero que un punto crítico $x$ de una función $f$ es aquel que al evaluarlo en la derivada de $f$ nos da la siguiente igualdad:
$$f'(x)=0.$$
Y que en el conjunto de estos puntos críticos se encontraban los máximos y mínimos de la función $f$.
En esta entrada daremos las definiciones formales correspondientes y veremos los Criterios de las derivadas para identificarlos. También veremos resultados en los que, haciendo uso de la derivada, podremos determinar si una función es creciente o decreciente en un intervalo.
Máximo y mínimo global
Definición: Sea $f: D_f \subseteq \r \rightarrow \r$ una función y $x_0 \in D_f$. Decimos que en $x_0$ se alcanza:
- Un máximo global si para toda $x \in D_f$ se cumple que:
$$f(x)\leq f(x_0).$$ - Un mínimo global si para toda $x \in D_f$ se cumple que:
$$f(x_0)\leq f(x).$$
Máximo y mínimo local
Definición: Consideremos a una función $f$ continua en un intervalo $I$ y $x_0 \in (x_0-r, x_0+r) \subseteq I$ con $r\in \r^{+}$ y tenemos que existe $f(x_0)$ decimos que:
- $x_0$ es un máximo local de $f \Leftrightarrow$ existe $r>0$ tal que para todo $x\in (x_0-r, x_0 +r)\subseteq D_f$ ocurre que:
$$f(x)\leq f(x_0).$$ - $x_0$ es un mínimo local de $f \Leftrightarrow$ existe $r>0$ tal que para todo $x\in (x_0-r, x_0 +r)\subseteq D_f$ ocurre que:
$$f(x_0)\leq f(x).$$ - $x_0$ no es máximo ni mínimo si existen $x_1, x_2$ tales que para toda $r>0$ y para cualquier $x\in(x_0-r, x_0 +r)$ ocurre que:
$$f(x_1)<f(x_0)<f(x_2).$$
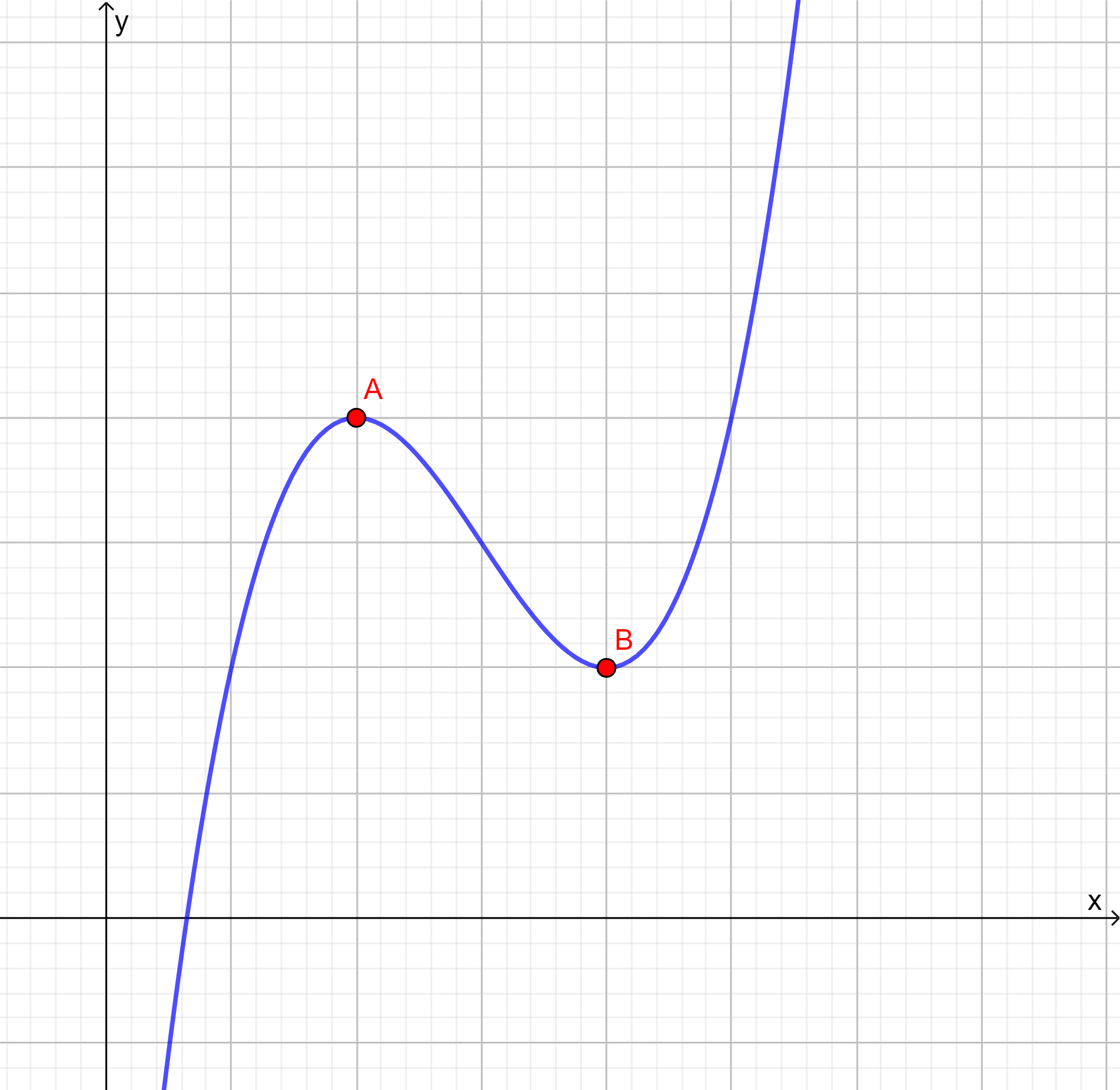
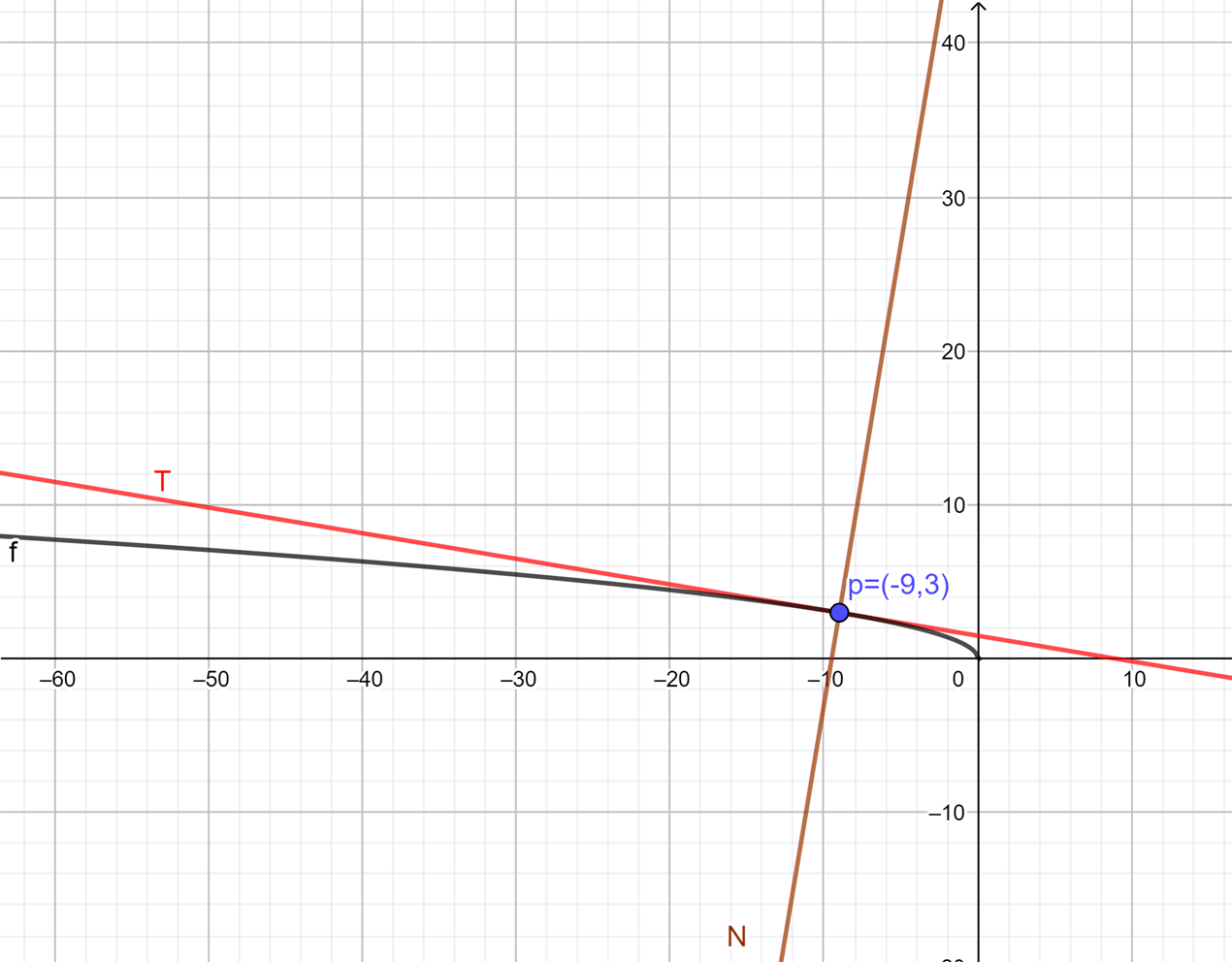
En la imagen anterior vemos que el punto $A$ es un máximo de la función y $B$ un mínimo.
La derivada y los puntos críticos
Teorema: Consideremos una función $f$ continua en un intervalo $I$ y es derivable en el punto $x_0 \in (x_0-r, x_0+r) \subseteq I$.
Si tenemos que $x_0$ es un máximo o un mínimo local de $f \Rightarrow f'(x_0)=0$.
Demostración: Tomemos $x_0$ máximo local de $f$, así por definición tenemos que existe $r_1>0$ tal que para cualquier $x \in (x_0-r_1, x_0+r_1)$ ocurre que:
$$ f(x) \leq f(x_0) .$$
O bien, si $x_0$ mínimo local de $f$ tenemos que existe $r_1>0$ tal que para cualquier $x \in (x_0-r_1, x_0+r_1)$ ocurre que:
$$f(x_0) \leq f(x).$$
Consideremos ahora $h$ tal que:
$$|h| \leq r_2= \text{min} \left\{r,r_1 \right\}.$$
Veremos el caso en que $x_0$ es máximo local de $f$.
Caso 1: Supongamos que $x_0$ es máximo.
Si tenemos que $h>0$ se sigue que:
\begin{align*}
f(x_0+h)< f(x_0) &\Rightarrow f(x_0+h)-f(x_0)<0\\
&\Rightarrow \frac{ f(x_0+h)-f(x_0) }{h}<0\\
&\Rightarrow \lim_{h \to 0^{+}} \frac{ f(x_0+h)-f(x_0) }{h} \leq 0\\
\end{align*}
Ya que $f$ es derivable en $x_0$ entonces podemos afirmar la siguiente igualdad:
$$ \lim_{h \to 0^{+}} \frac{ f(x_0+h)-f(x_0) }{h}=f'(x_0).$$
$$\therefore f'(x_0)\leq 0.$$
Ahora bien, si tenemos que $h<0$ tenemos que:
\begin{align*}
f(x_0+h)-f(x_0)<0 &\Rightarrow \frac{ f(x_0+h)-f(x_0) }{h}>0\\
&\Rightarrow \lim_{h \to 0^{-}} \frac{ f(x_0+h)-f(x_0) }{h}\geq 0
\end{align*}
$$\therefore f'(x_0) \geq 0.$$
$$\therefore 0\leq f'(x_0) \leq 0.$$
Y así concluimos que $f'(x_0)=0.$
$\square$
El Caso 2 considerando ahora que $x_0$ es mínimo se quedará como ejercicio de Tarea moral, para realizar la prueba se procede de manera análoga al caso que ya vimos.
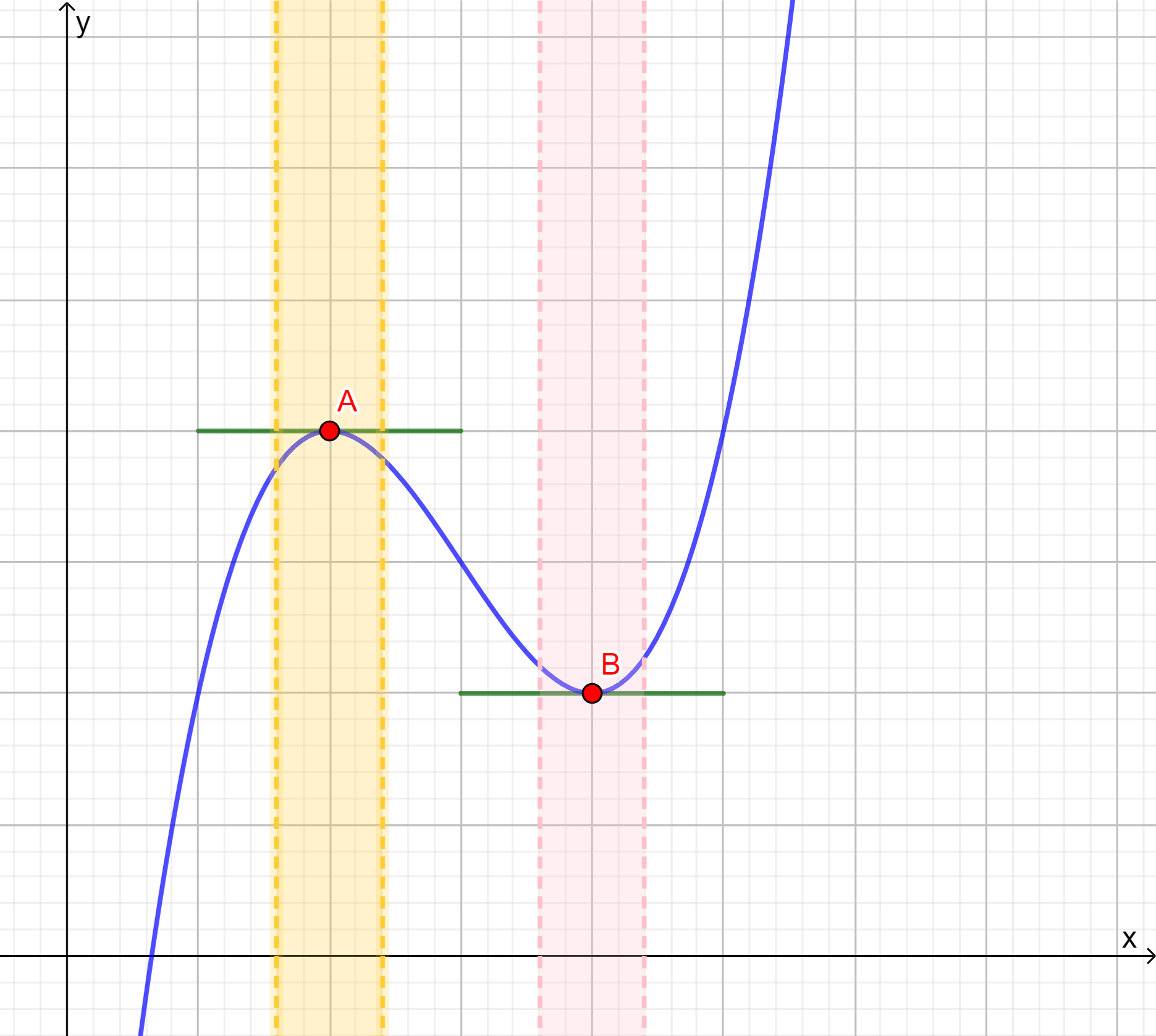
Gráficamente el resultado anterior se vería como sigue:
donde en el intervalo en el que se encuentra el punto $A$ la recta tangente a dicho punto tiene pendiente cero, es decir, es una recta horizontal. Observamos que para el intervalo (representado por la franja rosa) en el que se encuentra el punto $B$ tenemos una situación similar.
La derivada y la monotonía de las funciones
Teorema: Consideremos $f$ una función e $I$ un intervalo.
- Si $f'(x) > 0$ para todo $x\in I \Rightarrow f$ es creciente en $I$.
- Si $f'(x) \geq 0$ para todo $x\in I \Rightarrow f$ es no decreciente en $I$.
- Si $f'(x) < 0$ para todo $x\in I \Rightarrow f$ es decreciente en $I$.
- Si $f'(x) \leq 0$ para todo $x\in I \Rightarrow f$ es no creciente en $I$.
Demostración 1:
Queremos probar que para cualesquiera $x_1,x_2 \in I$ donde si $x_1<x_2$ entonces:
$$f(x_1)<f(x_2).$$
Así tomemos $x_1,x_2$ en el intervalo $I$ con $x_1 < x_2$. Veamos que $[x_1,x_2] \subseteq I$ y que $f$ es derivable en $(x_1,x_2) \subseteq I$. Y además tenemos que $f$ es continua en $[x_1,x_2] \subseteq I$, aplicando el Teorema del valor medio para la derivada:
$\exists \alpha \in (x_1,x_2)$ tal que $f'(\alpha)=\frac{f(x_2)-f(x_1)}{x_2-x_1}$.
Por hipótesis tenemos que:
$$ f'(\alpha)=\frac{f(x_2)-f(x_1)}{x_2-x_1} >0.$$
Debido a que también supusimos $x_2-x_1>0$ para que se cumpla la desigualdad anterior necesariamente debe ocurrir que:
$$f(x_2)-f(x_1)>0 \Rightarrow f(x_2)>f(x_1).$$
$\square$
Criterio de la primera derivada
Teorema (Criterio de la primera derivada): Si $f'(x_0)=0$ y existe $r>0$ tal que:
- Para todo $x \in (x_0-r,x_0)$, $f'(x)<0$ y para todo $x \in (x_0,x_0+r)$, $f'(x)>0$
$\Rightarrow x_0$ es mínimo local de $f$. - Para todo $x\in (x_0-r,x_0)$, $f'(x)>0$ y para todo $x \in (x_0,x_0+r)$, $f'(x)<0$
$\Rightarrow x_0$ es máximo local de $f$.
Demostración 1:
Sea $x \in (x_0-r, x_0)$ por hipótesis tenemos que $f'(x)<0$. Aplicando el teorema anterior afirmamos que $f$ es decreciente en $(x_0-r,x_0)$, así para cualquier $x < x_0$ en $(x_0-r, x_0)$:
$$f(x)>f(x_0).$$
Ahora tomando $x\in (x_0,x_0+r)$ tenemos que $f'(x)>0$. Y por el teorema anterior sabemos que $f$ es creciente en el intervalo $(x_0,x_0+r)$. Por definición para cualquier $x>x_0$ en $(x_0,x_0+r)$ ocurre que:
$$f(x_0)<f(x).$$
De lo anterior podemos concluir que para toda $x \in (x_0-r,x_0) \cup (x_0,x_0+r)= (x_0-r,x_0+r)$ se cumple la desigualdad:
$$f(x_0)<f(x).$$
que es justo la definición de $x_0$ mínimo local de $f$.
$\square$
A continuación veremos ejemplos donde aplicaremos los teoremas anteriores para localizar los máximos y mínimos de una función, como los intervalos donde es creciente o decreciente.
Ejemplo 1
Encuentra los puntos críticos de la siguiente función y determina si se trata de un máximo o un mínimo:
$$f(x)=(x-1)^{2}(x+1)^{3}$$
Solución:
Para encontrarlos seguiremos los siguientes pasos:
Paso 1: Hallamos la primera derivada de la función $f$.
\begin{align*}
f'(x)&= 2(x-1)(x+1)^{3}+3(x+1)^{2}(x-1)^{2}\\
&= (x-1)[2(x+1)^{3}+3(x+1)^{2}(x-1)]\\
&=(x-1)(x+1)^{2}[2(x+1)+3(x-1)]\\
&=(x-1)(x+1)^{2}[2x+2+3x+3]\\
&=(x-1)(x+1)^{2}(5x-1)\\
\therefore f'(x)&= (x-1)(x+1)^{2}(5x-1)
\end{align*}
Paso 2: Igualamos la derivada a cero para encontrar los puntos críticos.
$$f'(x)=0 \Leftrightarrow (x-1)(x+1)^{2}(5x-1) =0$$
El producto anterior lo cumple cuando:
\begin{align*}
(x+1)^{2} =0 & &\text{o}\quad 5x-1=0 & &\text{o}\quad x-1=0 \\
\sqrt{ (x+1)^{2}}= \sqrt{0} & &\text{o}\quad 5x=1& &\text{o}\quad x=1\\
x+1=0 & &\text{o}\quad x=\frac{1}{5}\\
x=-1
\end{align*}
Por lo que debemos determinar para $x=1$, $x=-1$ y $x=\frac{1}{5}$ si se trata de un máximo, un mínimo o ninguno de los dos.
Paso 3: Para determinar si es un máximo o mínimo, aplicando el Criterio de la primera derivada debemos sustituir en la primera derivada un valor $x_1<x$ para determinar si $f'(x_1)$ es positiva o negativa. De igual modo debemos evaluar una $x<x_2$ y obtener si $f'(x_2)$ es positiva o negativa.
Comencemos con $x=1$:
Si tomamos $x<1$ y sustituimos en $f'(x)=5(x-1)(x+1)^{2}(x-\frac{1}{5})$ a $x_1=\frac{1}{2}$ en la derivada
\begin{align*}
f’ \left(\frac{1}{2}\right)&= 5 \left(\frac{1}{2}-1\right) \left(\frac{1}{2}+1\right)^{2}\left(\frac{1}{2}-\frac{1}{5}\right)\\
&= 5\left(-\frac{1}{2}\right)\left(\frac{3}{2}\right)^{2}\left(\frac{3}{10}\right) \tag{que es negativo}
\end{align*}
Ahora para $x>1$ evaluamos $x_2=2$
\begin{align*}
f'(2)&= 5(2-1)(2+1)^{2}\left(2-\frac{1}{5}\right)\\
&=5(1)(3)^{2}\left(\frac{9}{5}\right) \tag{que es positivo}
\end{align*}
Ya que la derivada pasó de ser negativa a positiva tenemos que cuando $x=1$ la función tiene un mínimo.
$\therefore p_1=(1,0)$ es mínimo de $f$.
Continuemos con $x=-1$:
Para $x<-1$ tomaremos $x_1=-2$.
\begin{align*}
f'(-2)&=5(-2-1)(-2+1)^{2}\left(-2-\frac{1}{5}\right)\\
&=5(-3)(-1)^{2}\left(-\frac{11}{5}\right) \tag{que es positivo}
\end{align*}
Y para $x>-1$ consideramos ahora $x_2=-\frac{1}{2}$.
\begin{align*}
f’\left(-\frac{1}{2}\right)&=5\left(-\frac{1}{2}-1\right)^{2}\left(-\frac{1}{2}-\frac{1}{5}\right)\\
&=5\left(-\frac{3}{2}\right)\left(\frac{1}{2}\right)^{2}\left(-\frac{7}{10}\right)\tag{que es positivo}
\end{align*}
Debido a que la derivada no presenta cambio de signo, cuando $x=-1$ no es máximo ni mínimo.
Finalmente para $x=\frac{1}{5}$ análogamente procedemos:
Cuando $x< \frac{1}{5}$ sustituiremos $x_1=\frac{1}{6}$.
\begin{align*}
f’\left(\frac{1}{6}\right)&=5\left(\frac{1}{6}-1\right)\left(\frac{1}{6}+1\right)^{2}\left(\frac{1}{6}-\frac{1}{5}\right)\\
&=5\left(-\frac{5}{6}\right)\left(\frac{7}{6}\right)^{2}\left(-\frac{1}{30}\right)\tag{que es positivo}
\end{align*}
Ahora bien para $x>\frac{1}{5}$ evaluaremos $x_2=\frac{1}{2}$.
\begin{align*}
f’\left(\frac{1}{2}\right)&=5\left(\frac{1}{2}-1\right)\left(\frac{1}{2}+1\right)^{2}\left(\frac{1}{2}-\frac{1}{5}\right)\\
&=5\left(-\frac{1}{2}\right)\left(\frac{3}{2}\right)\left(\frac{3}{10}\right)\tag{que es negativo}
\end{align*}
Vemos que la derivada pasó de ser positiva a ser negativa, por lo tanto, cuando $x=\frac{1}{5}$ la función $f$ tiene un máximo.
$\therefore p_2=(0.2,1.10)$ es un máximo de $f$.
Ejemplo 2
Hallar los intervalos donde es creciente o decreciente la siguiente función:
$$f(x)=4x^{3}+3x^{2}-6x.$$
Solución:
Comenzaremos derivando la función y simplificando
\begin{align*}
f'(x)&= 12x^{2}+6x-6\\
&=6x^{2}+x-1\\
&=\left(x-\frac{1}{2}\right)(x+1)
\end{align*}
Sabemos que cuando $f'(x)>0$ la función es creciente, por ello veremos qué valores satisfacen la siguiente desigualdad:
$$\left(x-\frac{1}{2}\right)(x+1)>0.$$
El producto anterior cumple ser positivo cuando
Caso 1:
\begin{align*}
x -\frac{1}{2} >0 & &\text{y}\quad x+1>0\\
x > \frac{1}{2} & &\text{y}\quad x>-1\\
\end{align*}
Por lo que el intervalo solución para este caso es: $\left(\frac{1}{2}, \infty \right)$.
Caso 2:
\begin{align*}
x-\frac{1}{2}<0 & &\text{y}\quad x+1<0\\
x <\frac{1}{2} & &\text{y}\quad x<-1
\end{align*}
Así el intervalo solución es: $(-\infty, -1)$.
Concluimos que los intervalos donde $f$ es creciente son:
$$ (-\infty, -1) \cup \left(\frac{1}{2}, \infty \right).$$
Para encontrar donde la función es decreciente debemos trabajar con la desigualdad $f'(x)<0$, que sería:
$$\left(x-\frac{1}{2}\right)(x+1)<0.$$
Lo anterior se cumple en los siguientes casos:
Caso 3:
\begin{align*}
x-\frac{1}{2}>0 & &\text{y}\quad x+1<0\\
x>\frac{1}{2} & &\text{y}\quad x<-1
\end{align*}
Vemos que la solución de este caso es vacía.
Caso 4:
\begin{align*}
x-\frac{1}{2}<0 & &\text{y}\quad x+1>0\\
x<\frac{1}{2} & &\text{y}\quad x>-1
\end{align*}
El intervalo que cumple lo anterior es $\left(-1,\frac{1}{2}\right)$.
De los casos anteriores tenemos que $f$ es decreciente en el intervalo:
$$ \left(-1,\frac{1}{2}\right) $$
Más adelante
En la siguiente entrada seguiremos trabajando con los máximos y mínimos de funciones, por lo que te presentaremos una herramienta más para poder localizarlos: el Criterio de la segunda derivada. También veremos cómo determinar las regiones de concavidad o convexidad de una función y sus puntos de inflexión.
Tarea moral
- Da la demostración del teorema para el caso en que $x_0$ es un mínimo local de $f$.
- Prueba los siguientes puntos:
- Si $f'(x) \geq 0$ para todo $x\in I \Rightarrow f$ es no decreciente en $I$.
- Si $f'(x) < 0$ para todo $x\in I \Rightarrow f$ es decreciente en $I$.
- Si $f'(x) \leq 0$ para todo $x\in I \Rightarrow f$ es no creciente en $I$.
- Determina si los siguientes enunciados son verdaderos o falsos. De ser verdadero da la demostración correspondiente, de lo contrario da un contraejemplo:
- Si $f$ es una función creciente, derivable y continua en un intervalo $I \Rightarrow f'(x)>0$ para toda $x\in I$.
- Si $f$ es una función estrictamente creciente, continua y derivable en $I \Rightarrow f'(x)>0$ para toda $x\in I$.
- Realiza la gráfica de la función:
$$f(x)=\frac{1}{(x-1)^{2}}+1.$$
Determinando los intervalos donde $f$ es creciente o decreciente.
Señalando si es que existen:- máximos y mínimos (locales y globales).
- los valores $x$ donde $f(x)=0$.
- $\lim_{x \to \infty^{+}} f(x)$.
- $\lim_{x \to \infty^{-}} f(x)$.
Entradas relacionadas
- Ir a: Cálculo Diferencial e Integral I
- Entrada anterior del curso: Cálculo Diferencial e Integral I: Rectas tangente y normal a una curva.
- Entrada siguiente del curso: Cálculo Diferencial e Integral I: Localización de máximos y mínimos. Regiones de convexidad y puntos de inflexión.
- Resto de cursos: Cursos
Agradecimientos
Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»