Introducción
En esta entrada hablaremos sobre algunas propiedades importantes del cuadrilátero cíclico, mas allá de las primeras caracterizaciones como las vistas en el teorema de Ptolomeo.
Fórmula de Brahmagupta
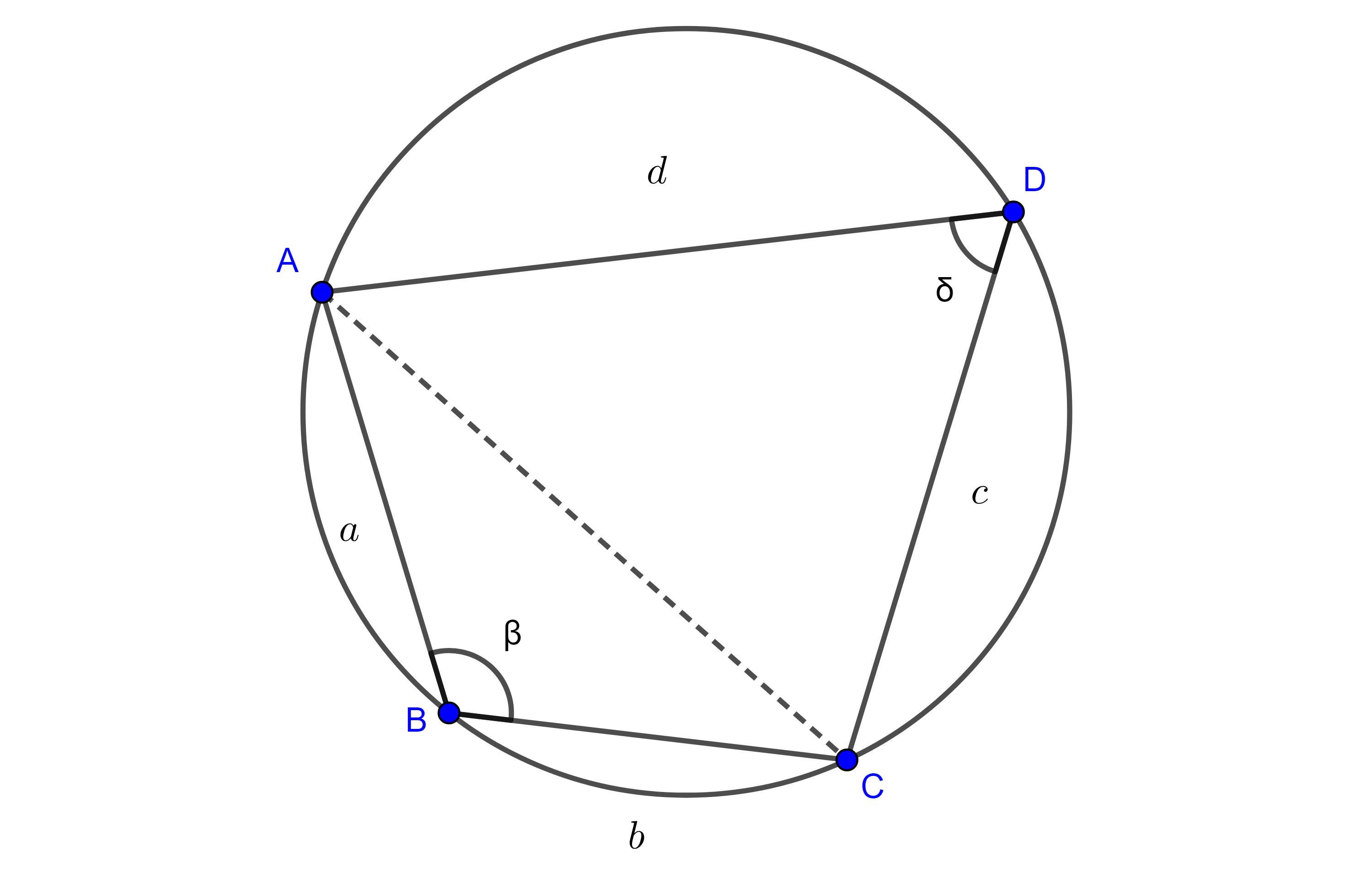
Teorema 1, fórmula de Bretschneider. Sea $\square ABCD$ un cuadrilátero convexo, si $AB = a$, $BC = b$, $CD = c$, $AD = d$, $s = \dfrac{a + b + c + d}{2}$ y $\beta = \angle CBA$, $\delta = \angle ADC$, entonces el área de $\square ABCD$ se puede calcular mediante la siguiente formula:
$(\square ABCD) = \sqrt{(s – a)(s – b)(s – c)(s – d) – \dfrac{abcd}{2}(1 + \cos(\beta + \delta))}$
Demostración. Calculamos el área de los triángulos que se forman al considerar la diagonal AC,
$(\triangle ABC) = \dfrac{ab \sin \beta}{2}$,
$(\triangle ACD) = \dfrac{cd \sin \delta}{2}$.
Por otro lado, empleando la ley de los cosenos podemos calcular $AC$
$AC^2 = a^2 + b^2 – 2ab \cos \beta = c^2 + d^2 – 2cd \cos \delta$.
De la última igualdad obtenemos
$(a^2 + b^2 – (c^2 + d^2))^2 = (2ab \cos \beta – 2cd \cos \delta)^2$.
Entonces:
$(\square ABCD) = (\triangle ABC) + (\triangle ACD) = \dfrac{ab \sin \beta}{2} + \dfrac{cd \sin \delta}{2}$
$\Rightarrow (\square ABCD)^2 = \dfrac{a^2b^2 \sin^2 \beta}{4} + \dfrac{abcd \sin \beta \sin \delta }{2} + \dfrac{c^2d^2 \sin^2 \delta}{4}$.
Por lo tanto,
$16(\square ABCD)^2 = 4 a^2b^2 \sin^2 \beta + 8 abcd \sin \beta \sin \delta + 4 c^2d^2 \sin^2 \delta$
$= 4a^2b^2(1 – \cos^2 \beta) + 4c^2d^2(1 – \cos^2 \delta) + 8abcd \sin \beta \sin \delta$
$= 4a^2b^2 + 4c^2d^2 + 8abcd – 8abcd – 4a^2b^2 \cos^2 \beta – 4c^2d^2 \cos^2 \delta$
$+ 8abcd\cos \beta\cos \delta – 8abcd\cos \beta\cos \delta + 8abcd \sin \beta \sin \delta$
$= (2ab + 2cd)^2 – (2ab \cos \beta – 2cd \cos \delta)^2 – 8abcd(1 + \cos \beta\cos \delta – \sin \beta \sin \delta)$
$ = (2ab + 2cd)^2 – (a^2 + b^2 – (c^2 + d^2))^2 – 8abcd(1 + \cos(\beta + \delta))$
$= (2ab + 2cd + a^2 + b^2 – (c^2 + d^2))(2ab + 2cd – a^2 – b^2 + (c^2 + d^2)) – 8abcd(1 + \cos(\beta + \delta))$
$ = (a^2 + 2ab +b^2 – (c^2 – 2cd + d^2))(c^2 + 2cd + d^2 – (a^2 – 2ab + b^2)) – 8abcd(1 + \cos(\beta + \delta))$
$=((a + b)^2 – (c – d)^2)((c + d)^2 – (a – b)^2) – 8abcd(1 + \cos(\beta + \delta))$
$=(a + b + c – d)(a + b + d – c)(a + c + d – b)(b + c + d – a) – 8abcd(1 + \cos(\beta + \delta))$
$= (2s – 2d)(2s – 2c)(2s – 2b)(2s – 2a) – 8abcd(1 + \cos(\beta + \delta))$
$\Rightarrow (\square ABCD) = \sqrt{(s – a)(s – b)(s – c)(s – d) – \dfrac{1}{2}abcd(1 + \cos(\beta + \delta))}$.
$\blacksquare$
Corolario, fórmula de Brahmagupta. Si $\square ABCD$ es cíclico entonces
$(\square ABCD) = \sqrt{(s – a)(s – b)(s – c)(s – d)}$.
Demostración. Si $\square ABCD$ es cíclico entonces $\beta + \delta = \pi$
por lo que $1 + \cos(\beta + \delta) = 0$.
$\blacksquare$
Observación. La fórmula de Bretschneider nos muestra que de todos los cuadriláteros convexos que tienen lados $a$, $b$, $c$ y $d$, aquellos que son cíclicos tienen mayor área.
Una propiedad del cuadrado
Teorema 2. De entre los cuadriláteros con el mismo perímetro el cuadrado es el que tiene la mayor área.
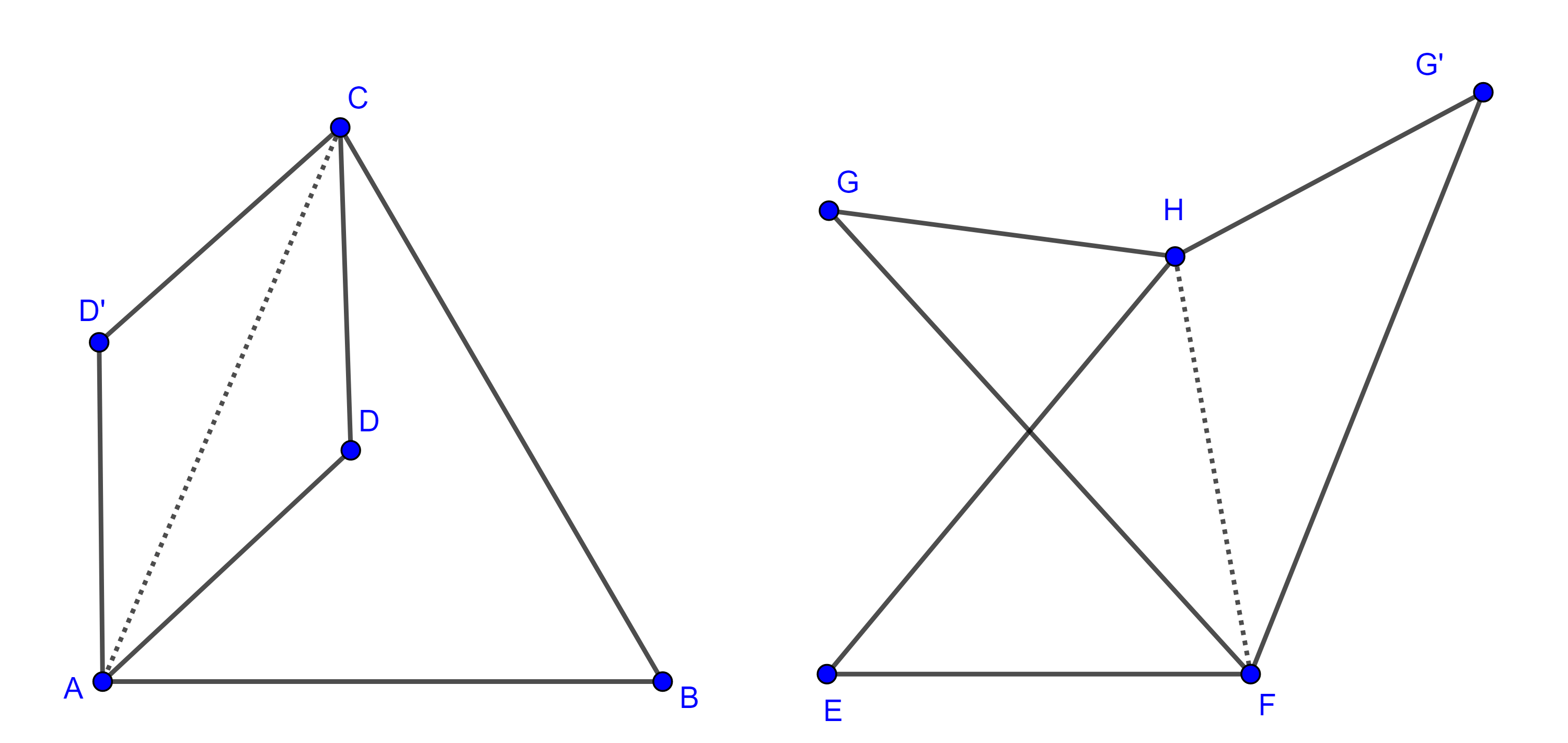
Demostración. Notemos primero que a partir de un cuadrilátero cóncavo o un cuadrilátero cruzado con un perímetro dado es posible construir un cuadrilátero convexo que tenga los mismos lados, pero mayor área.
Si en el cuadrilátero cóncavo $\square ABCD$, reflejamos $D$ respecto la diagonal $AC$ obtenemos $\square ABCD’$ el cual es convexo y $(\square ABCD’) = (\square ABCD) + (\square ADCD’)$.
Por lo tanto $(\square ABCD’) > (\square ABCD)$.
En el caso de un cuadrilátero cruzado reflejamos algún vértice respecto de la diagonal que no pasa por el vértice a reflejar, por ejemplo, en $\square EFGH$ reflejamos $G$ respecto de $\overline{FH}$ y obtenemos $\square EFG’H$.
Por lo tanto,
$(\square EFG’H) = (\triangle EFH) + (\triangle FG’H) = (\triangle EFH) + (\triangle FGH) > (\square EFGH)$.
De esta forma podemos fijarnos solo en el área de los cuadriláteros convexos, pero por la observación bastara con restringirnos a los cuadriláteros convexos y cíclicos.
Por la fórmula de Brahmagupta sabemos que el área depende de los lados del cuadrilátero cíclico.
En la entrada desigualdades geométricas vimos que para $w$, $x$, $y$, $z$ números reales positivos tesemos lo siguiente:
$wxyz \leq (\dfrac{w + x + y + z}{4})^4$, y la igualdad se da si y solo si $w = x = y = z$.
Aplicamos este resultado al área del cuadrilátero cíclico $\square ABCD$ de perímetro $P$ y lados $a$, $b$, $c$ y $d$.
$(\square ABCD)^2 = (s – a)(s – b)(s – c)(s – d) \leq (\dfrac{(s – a) + (s – b) + (s – c) + (s – d)}{4})^4$
$= (\dfrac{(4s – (a + b + c + d)}{4})^4 = (\dfrac{2P – P}{4})^4 = (\dfrac{P}{4})^4$
Por lo tanto,
$(\square ABCD) \leq (\dfrac{P}{4})^2$ y la igualdad se da
$\Leftrightarrow$ $(s – a) = (s – b) = (s – c) = (s – d)$
$ \Leftrightarrow$$ a = b = c = d$
$\Leftrightarrow \square ABCD$ es un cuadrado.
$\blacksquare$
Anticentro del cuadrilátero cíclico
Definición. Las rectas perpendiculares a los lados de un cuadrilátero que pasan por los puntos medios de los lados opuestos, se conocen como $m$-alturas.
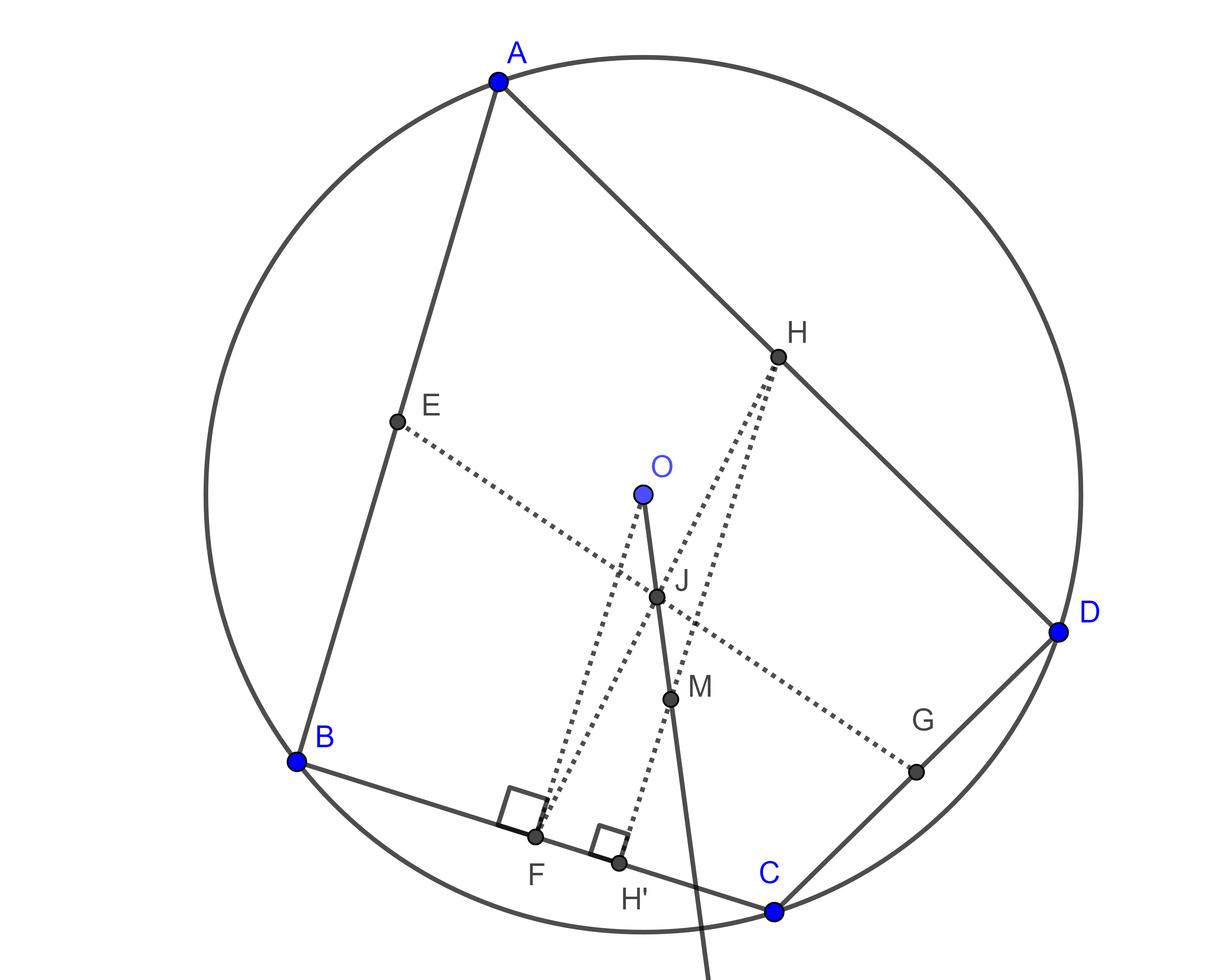
Teorema 3. Las $m$-alturas de un cuadrilátero cíclico son concurrentes, al punto de concurrencia se le conoce como anticentro, además, el circuncentro, el centroide y el anticentro de un cuadrilátero cíclico son colineales.
Demostración. Sea $\square ABCD$ cíclico y sean $E$, $F$, $G$ y $H$ los puntos medios de $AB$, $BC$, $CD$ y $DA$ respectivamente consideremos $O$ y $J$, el circuncentro y el centroide respectivamente de $\square ABCD$.
La perpendicular a $BC$ desde $H$ interseca a $BC$ en $H’$, $HH’$ interseca a la recta determinada por $O$ y $J$ en $M$.
Como $O$ esta en la mediatriz de $BC$ entonces $OF \perp BC$, y asi, $OF \parallel HH’$, en consecuencia $\angle JFO = \angle JHM$, además $\angle OJF = \angle MJH$ por ser opuestos por el vértice.
Por lo tanto, $\triangle JFO$ y $\triangle JHM$ son semejantes y como $J$ es el punto medio de $HF$, entonces, $JO = JM$, en otras palabras, $HH’$ pasa por $M$, el punto simétrico de $O $ respecto a $J$.
De manera similar podemos ver que las demás $m$-alturas de $\square ABCD$ pasan por $M$.
$\blacksquare$
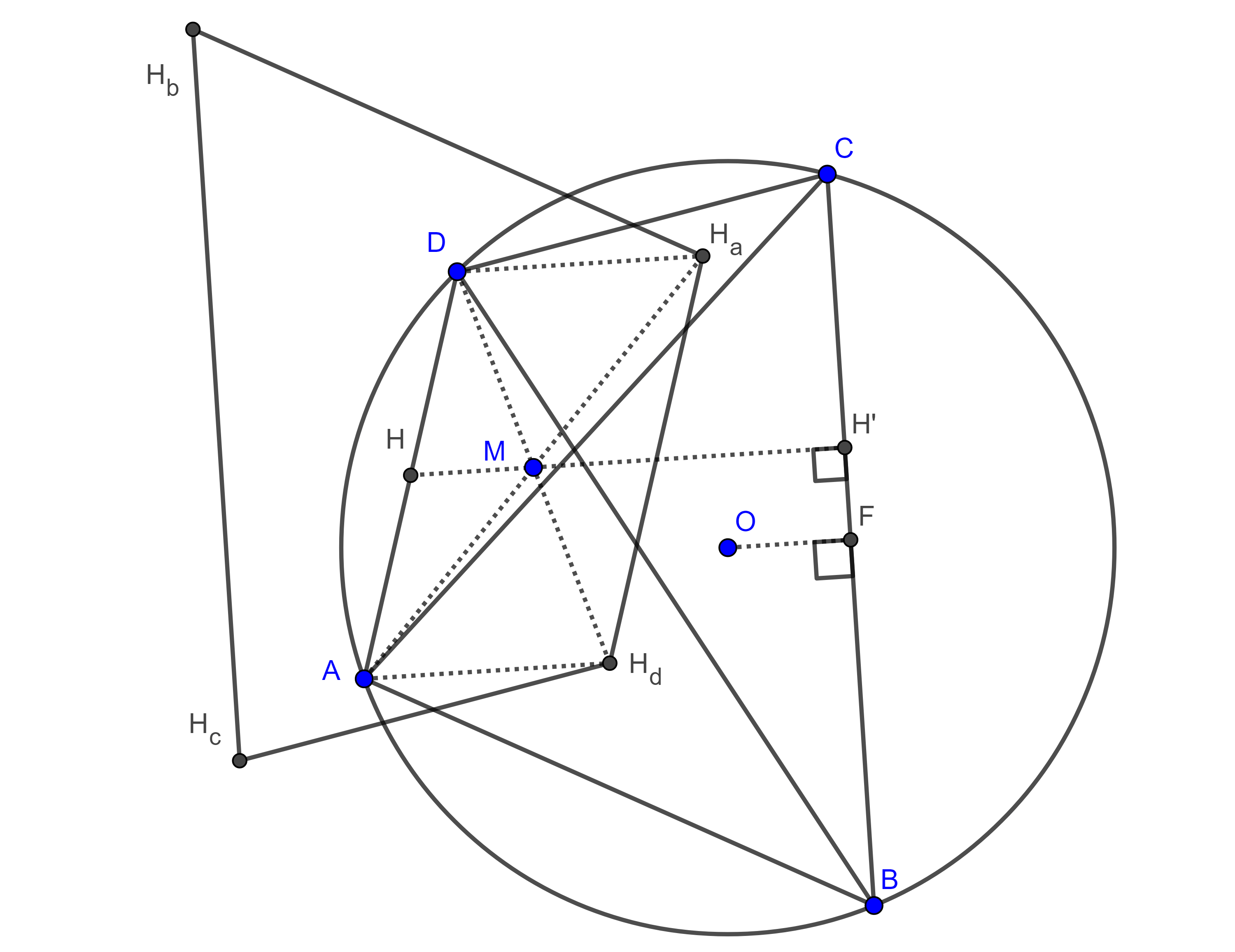
Proposición 1. Los ortocentros de los triángulos determinados por los cuatro vértices de un cuadrilátero cíclico forman un cuadrilátero simétrico al cuadrilátero original respecto del anticentro.
Demostración. Sean $\square ABCD$ cíclico y $H_{a}$, $H_{b}$, $H_{c}$ y $H_{d}$ los ortocentros de $\triangle BCD$, $\triangle ACD$, $\triangle ABD$ y $\triangle ABC$ respectivamente y $F$ el punto medio de $BC$.
Considerando los triángulos $\triangle ABC$ y $\triangle DBC$ y por la proposición 6 de la entrada triangulo órtico, tenemos que $AH_{d} = 2OF = DH_{a}$, además $AH_{d}$ y $DH_{a}$ son perpendiculares a $BC$ por lo tanto $AH_{d} \parallel DH_{a}$.
De esto se sigue que $\square AH_{d}H_{a}D$ es un paralelogramo, así que las diagonales $AH_{a}$ y $DH_{d}$ se intersecan en su punto medio.
De manera análoga vemos que $AH_{a}$ y los segmento $BH_{b}$, $CH_{c}$, se intersecan en su punto medio.
Por lo tanto, estos cuatro segmentos se bisecan mutuamente, es decir el punto de intersección $X$ es el centro de simetría de $\square ABCD$ y $\square H_{a}H_{b}H_{c}H_{d}$.
Ahora en $\triangle AH_{d}D$ consideremos la recta que pasa por $H$ el punto medio de $DA$ y el centro de simetría $X$, entonces $HX \parallel AH_d$, por lo tanto, $HX \perp $BC$ y así $HX$ es una $m$-altura.
De manera análoga vemos que las otras $m$-alturas pasan por $X$, por lo tanto, $X$ es el anticentro de $\square ABCD$.
$\blacksquare$
Teorema Japonés
Proposición 2. Sea $\square ABCD$ cíclico, considera $E$, $F$, $G$, $H$, los puntos medios de los arcos, $BC$, $CD$, $DA$, $AB$, respectivamente del circuncírculo de $\square ABCD$, entonces $EG \perp FH$.
Demostración. Considera $O$ el circuncentro de $\square ABCD$ y $X = EG \cap FH$.
Como $\angle EXF$ es un ángulo interior, tenemos lo siguiente:
$\angle EXF = \dfrac{\angle EOF + \angle GOH}{2}$
$= \angle EAF + \angle GCH = \angle EAC + \angle CAF + \angle GCA + \angle ACH $
$= \dfrac{\angle BAC}{2} + \dfrac{\angle CAD}{2} + \dfrac{\angle DCA}{2} + \dfrac{\angle ACB}{2} $
$ = \dfrac{\angle BAD + \angle DCB}{2} = \dfrac{\pi}{2}$.
$\blacksquare$
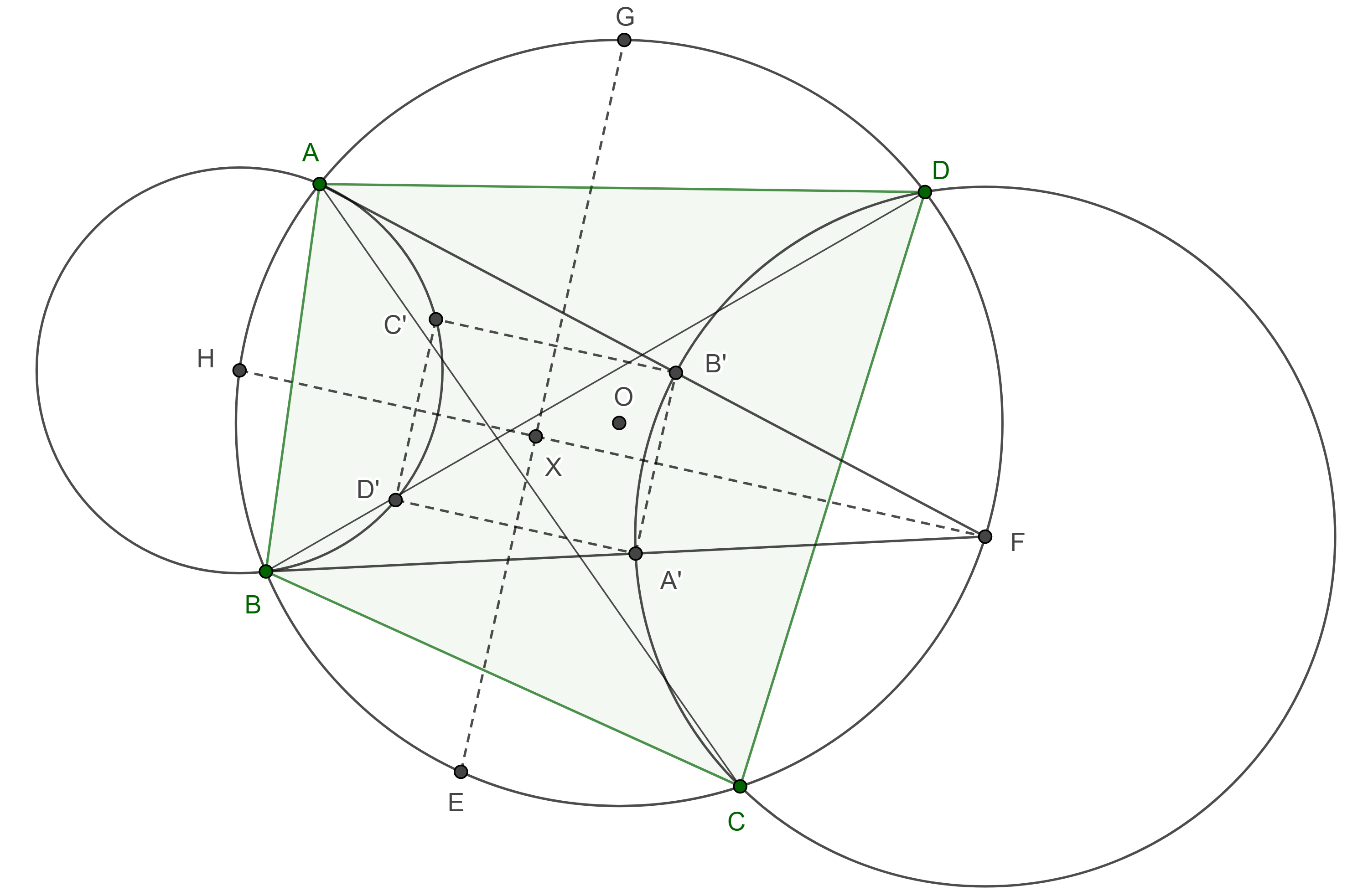
Teorema 4, teorema japonés. Los incentros de los cuatro triángulos que se forman al considerar las diagonales de un cuadrilátero cíclico, son los vértices de un rectángulo.
Demostración. Sean $A’$, $B’$, $C’$, $D’$, los incentros de $\triangle BCD$, $\triangle ACD$, $\triangle ABD$, $\triangle ABC$, donde $\square ABCD$ es cíclico (figura 5).
En $\triangle ACD$, como $AB’$ es la bisectriz de $\triangle CAD$ entonces $AB’$ interseca al circuncírculo de $\square ABCD$ en $F$ el punto medio del arco $\overset{\LARGE{\frown}}{CD}$.
Por el teorema 1 de la entrada circunferencias tritangentes, $B’$ pertenece a la circunferencia $(F, FC)$, con centro en $F$ y radio $FC = FD$.
De manera análoga podemos ver que $A’ \in (F, FC)$, por lo tanto, $\triangle A’FB’$ es isósceles.
Sea $H$ el punto medio del arco $\overset{\LARGE{\frown}}{AB}$, entonces $FH$ es bisectriz de $\triangle AFB$, en consecuencia, $A’B’ \perp FH$.
De mamera análoga vemos que $C’D’ \perp FH$ y $B’C’ \perp EG \perp D’A’$, donde $E$ y $G$ son los puntos medios de los arcos $\overset{\LARGE{\frown}}{BC}$ y $\overset{\LARGE{\frown}}{DA}$ respectivamente.
Por la proposición anterior, $EG \perp FH$, por lo tanto, $\square A’B’C’D’$ es un rectángulo.
$\blacksquare$
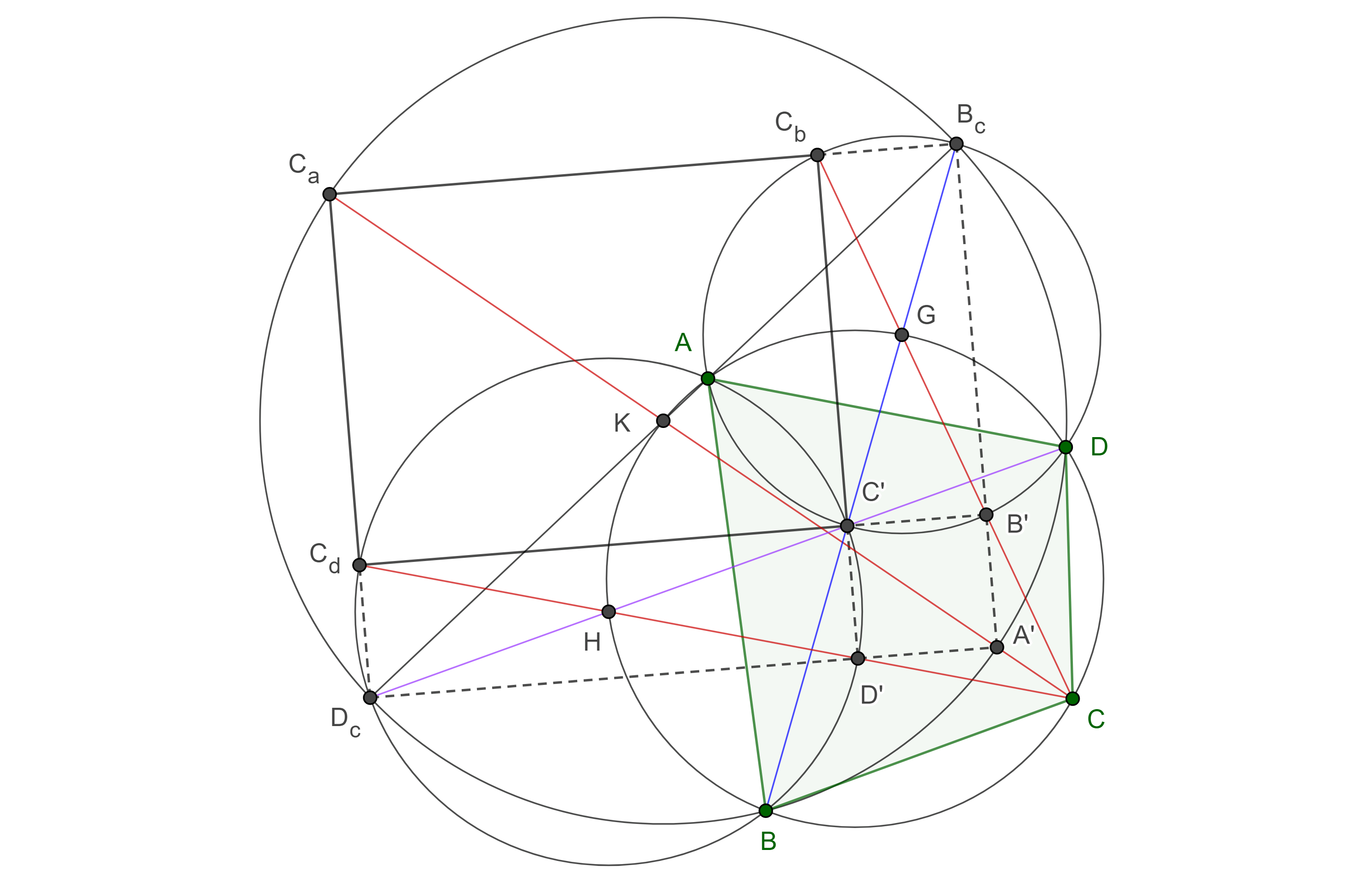
Teorema 5. De los cuatro triángulos que se forman al trazar las diagonales de un cuadrilátero cíclico, si consideremos tres que comparten un mismo vértice, entonces los tres excentros opuestos al vértice que comparten, son los vértices de un rectángulo, y el cuarto vértice es el incentro del triángulo restante.
Demostración. Usaremos la misma notación del teorema anterior.
En $\square ABCD$, consideremos los tres triángulos que comparten el vértice $C$, $\triangle CDB$, $\triangle CDA$, $\triangle CAB$ y sus respectivos excentros opuestos a $C$, $C_a$, $C_b$, $C_d$.
Nos apoyaremos en el teorema 1 de la entrada circunferencias tritangentes para hacer las siguientes afirmaciones.
$D’C_d$ es diámetro de la circunferencia $(H, HA)$, con centro en $H$ el punto medio de $\overset{\LARGE{\frown}}{AB}$, y radio $HA = HB = HC’$.
Consideremos $D_c$ el excentro de $\triangle ABD$ opuesto a $D$, $C’D_c$ es diámetro de $(H, HA)$.
Como $D’C_d$ y $C’D_c$, se bisecan y tienen la misma longitud, entonces, $\square C_dD_CD’C’$ es un rectángulo.
En consecuencia, las dos tercias de puntos, $C_d$, $C’$, $B’$; $D_c$, $D’$, $A’$, son colineales.
Igualmente, si consideramos $B_c$ el excentro de $\triangle ABD$ opuesto a $B$, podemos ver $B’C_b$ y $C’B_c$ son diámetros de $(G, GA)$ con $G$ el punto medio de $\overset{\LARGE{\frown}}{DA}$ y que las dos tercias $C_b$, $C’$, $D’$; $B_C$, $B’$, $A’$, son colineales.
Por otra parte, como $B_c$, $D_c$ son excentros de $\triangle ABD$, entonces $B_cD_c$ es diámetro de $(K, KB)$, la circunferencia con centro en $K$, el punto medio de $\overset{\LARGE{\frown}}{DB}$, y radio $KB = KD$.
Similarmente, como $A’$ y $C_a$, son dos centros tritangentes de $\triangle CBD$ entonces $A’C_a$ es diámetro de $(K, KB)$.
Por lo tanto, $\square C_aD_cA’B_c$ es un rectángulo.
En consecuencia, $\square C_aC_dC’C_b$ es un rectángulo.
$\blacksquare$
Más adelante…
En la siguiente entrada estudiaremos propiedades de los cuadriláteros cuyas diagonales son perpendiculares y veremos que pasa cuando además son cíclicos.
Tarea moral
A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.
- Demuestra la fórmula de Brahmagupta usando la fórmula de Herón.
- En la tarea moral de la entrada teorema de Ptolomeo se pide mostrar que es posible construir tres cuadriláteros cíclicos diferentes de lados $a$, $b$, $c$ y $d$ siempre que la suma de cualesquiera tres de ellos sea mayor que el restante, y que de estos se obtienen tres diagonales diferentes digamos $l$, $m$, y $n$ si $\square ABCD$ es construido de esa manera y $R$ es el circunradio muestra que:
$i)$ $(\square ABCD) = \dfrac{lmn}{4R}$
$ii)$ $(\square ABCD)^2 = \dfrac{(ab + cd)(ac + bd)(ad + bc)}{16R^2}$. - Demuestra que los centroides de los cuatro triángulos determinados por los cuatro vértices de un cuadrilátero cíclico son los vértices de otro cuadrilátero cíclico.
- Muestra que la suma de los cuadrados de las distancias del anticentro de un cuadrilátero cíclico a los cuatro vértices es igual al cuadrado del diámetro de la circunferencia en la que esta inscrito dicho cuadrilátero.
- Muestra que el anticentro de un cuadrilátero cíclico es el ortocentro del triángulo formado por los puntos medios de las diagonales y el punto en que estas rectas coinciden.
- Prueba que las circunferencia de los nueve puntos de los cuatro triángulos que se forman al considerar las dos diagonales de un cuadrilátero cíclico, concurren en el anticentro del cuadrilátero.
- Demuestra que la suma de los inradios de los triángulos obtenidos al trazar una diagonal de un cuadrilátero cíclico es igual a la suma de los inradios de los otros dos triángulos que se obtienen al considerar la otra diagonal.
Entradas relacionadas
- Ir a Geometría Moderna I.
- Entrada anterior del curso: Teoremas de Varignon y Van Aubel.
- Siguiente entrada del curso: Cuadrilátero ortodiagonal.
- Otros cursos.
Fuentes
- Gomez, A. y Bulajich, R., Geometría. México: Instituto de Matemáticas, 2002, pp 143-146.
- Altshiller, N., College Geometry. New York: Dover, 2007, pp 127-135.
- Coxeter, H. y Greitzer, L., Geometry Revisited. Washington: The Mathematical Association of America, 1967, pp 57-60.
- Wikipedia
Agradecimientos
Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»