Introducción

Decimos que un cuadrilátero convexo es ortodiagonal si sus diagonales son perpendiculares. En esta entrada veremos algunas propiedades del cuadrilátero ortodiagonal.

Dos caracterizaciones para el cuadrilátero ortodiagonal

Teorema 1. Un cuadrilátero convexo es ortodiagonal si y solo si la suma de los cuadrados de dos lados opuestos es igual a la suma de los cuadrados de los restantes lados opuestos.

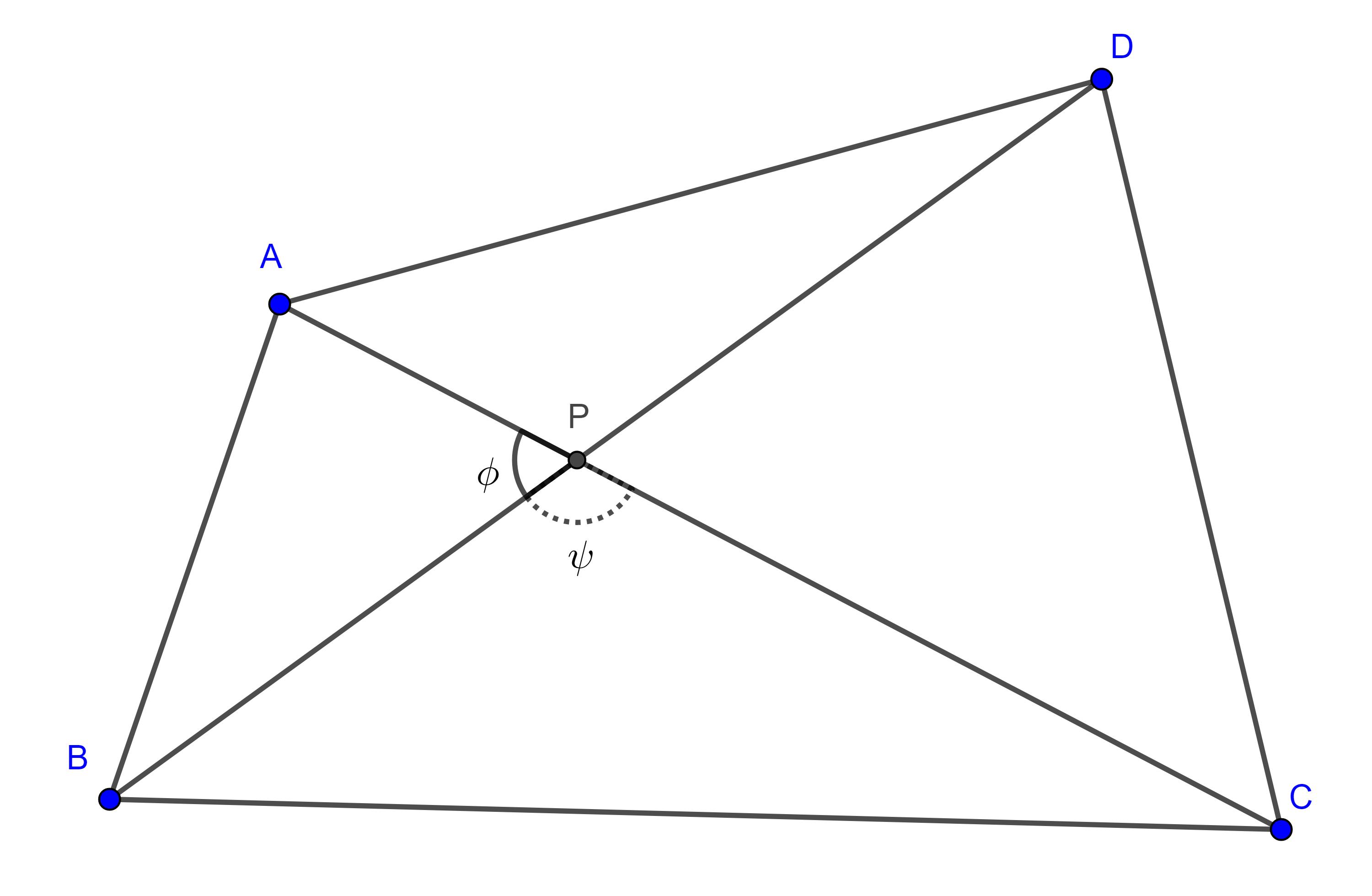
Demostración. Sea $\square ABCD$ convexo, consideremos $P$ la intersección de las diagonales, $\phi = \angle APB$, $\psi = \angle BPC$.

Como $\phi + \psi = \pi$ entonces $\cos \phi = – \cos \psi$.

Aplicando la ley de los cosenos a los triángulos $\triangle APB$, $\triangle BPC$, $\triangle CPD$ y $\triangle APD$ obtenemos,
$AB^2 = AP^2 + BP^2 – 2AP \times BP \cos \phi$,
$BC^2 = BP^2 + CP^2 – 2BP \times CP \cos \psi$,
$CD^2 = CP^2 + DP^2 – 2CP \times DP \cos \phi$,
$AD^2 = AP^2 + DP^2 – 2AP \times DP \cos \psi$.

Por lo tanto,
$AB^2 + CD^2 – BC^2 – AD^2 $
$= (AP^2 + BP^2 + 2AP \times BP \cos \psi) + (CP^2 + DP^2 + 2CP \times DP \cos \psi)$
$- (BP^2 + CP^2 – 2BP \times CP \cos \psi) – (AP^2 + DP^2 – 2AP \times DP \cos \psi)$
$= 2 \cos \psi (AP \times BP + CP \times DP + BP \times CP + AP \times DP)$.

Notemos que $0 < \psi < \pi$, por lo tanto,
$\overline{AC} \perp \overline{BD} \Leftrightarrow  \psi = \dfrac{\pi}{2} \Leftrightarrow  \cos \psi = 0$
$\Leftrightarrow  AB^2 + CD^2 = BC^2 + AD^2$.

$\blacksquare$

Proposición 1. Sean $\square ABCD$ convexo, $P$ la intersección de las diagonales, $m_{i}$ con $i = 1, 2, 3, 4$ las medianas de los triángulos $\triangle APB$, $\triangle BPC$, $\triangle CPD$ y $\triangle APD$, que pasan por $P$, entonces $\square ABCD$ es ortodiagonal si y solo si $m_{1}^2 + m_{3}^2 = m_{2}^2 + m_{4}^2$.

Demostración. Aplicando el teorema de Apolonio para calcular la longitud de las medianas en términos de los lados de sus respectivos triángulos obtenemos,

$m_{1}^2 + m_{3}^2 = m_{2}^2 + m_{4}^2$
$\Leftrightarrow  4m_{1}^2 + 4m_{3}^2 = 4m_{2}^2 + 4m_{4}^2$
$\Leftrightarrow  2(AP^2 + BP^2) – AB^2 + 2(CP^2 + DP^2) – CD^2$
$ = 2(BP^2 + CP^2) – BC^2 + 2(AP^2 + DP^2) – AD^2$
$\Leftrightarrow  AB^2 + CD^2 = BC^2 + AD^2$.

La última doble implicación es cierta por el teorema 1.

$\blacksquare$

Circunferencia de los 8 puntos del cuadrilátero ortodiagonal

Definición. Al cuadrilátero formado por los pies de las $m$-alturas de un cuadrilátero convexo se le conoce como cuadrilátero principal órtico.

Lema 1. Los vértices del paralelogramo de Varignon y los vértices del cuadrilátero principal órtico de un cuadrilátero convexo que se encuentran sobre lados opuestos, están en dos circunferencias con centro en $G$, el centroide del cuadrilátero.

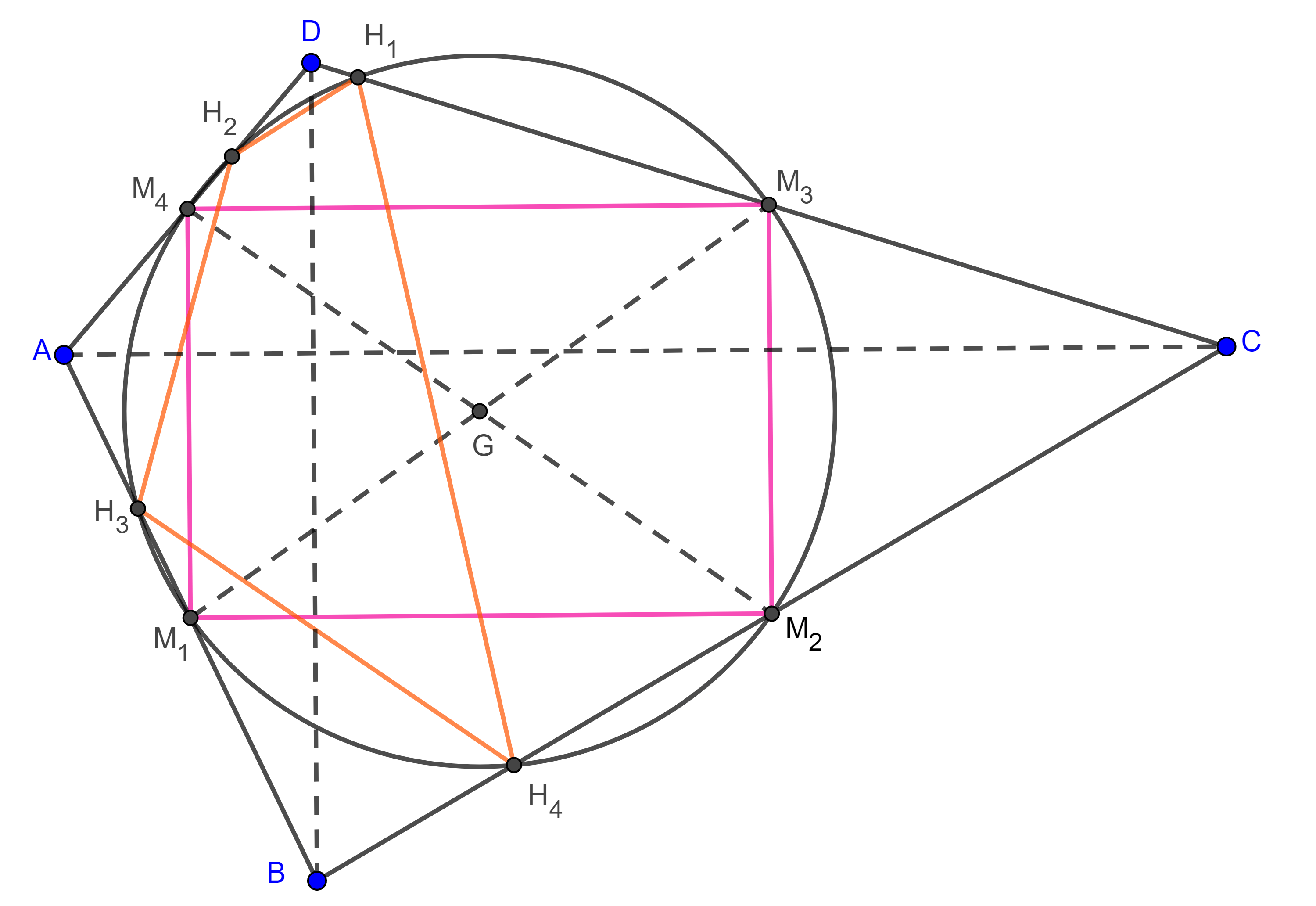
Demostración. Sean $\square ABCD$ un cuadrilátero convexo $M_{1}$, $M_{2}$, $M_{3}$ y $M_{4}$ los puntos medios de $AB$, $BC$, $CD$ y $AD$ respectivamente.

Recordemos que las diagonales del cuadrilátero de Varignon, es decir, las bimedianas $M_{1}M_{3}$ y $M_{2}M_{4}$, se intersecan en su punto medio, $G$, al que llamamos centroide.

Sean $M_{1}H_{1}$, $M_{2}H_{2}$, $M_{3}H_{3}$ y $M_{4}H_{4}$ las $m$-alturas de $\square ABCD$.

Por construcción $\angle M_{3}H_{1}M_{1} = \angle M_{1}H_{3}M_{3} = \dfrac{\pi}{2}$, por lo tanto, $M_{1}M_{3}$ es el diámetro de una circunferencia con centro en $G$ y que pasa por $H_{1}$ y $H_{3}$.

De manera análoga podemos ver que los puntos $H_{2}$ y $H_{4}$ están en una circunferencia de diámetro $M_{2}M_{4}$ con centro en $G$.

$\blacksquare$

Teorema 2. Los vértices del paralelogramo de Varignon y los vértices del cuadrilátero principal órtico de un cuadrilátero convexo están en una misma circunferencia con centro en el centroide del cuadrilátero si y solo si el cuadrilátero es ortodiagonal.

A dicha circunferencia se le conoce como primera circunferencia de los ocho puntos del cuadrilátero ortodiagonal.

Demostración. El lema anterior nos dice que los puntos ${M_{1}, H_{1}, M_{3}, H_{3}}$ y ${M_{2}, H_{2}, M_{4}, H_{4}}$ están en dos circunferencias con centro en $G$, el centroide de $\square ABCD$.

Además, las bimedianas de un cuadrilátero se bisecan en el centroide del cuadrilátero.

Por lo tanto, el paralelogramo de Varignon y el cuadrilátero principal órtico son ambos cíclicos y comparten la misma circunferencia si y solo si $M_{1}M_{3} = M_{2}M_{4}$, es decir, las bimedianas tienen la misma longitud, si y solo si el paralelogramo de Varignon es un rectángulo si y solo si $\square ABCD$  es ortodiagonal.

$\blacksquare$

Teorema de Brahmagupta

Teorema 3. de Brahmagupta. En un cuadrilátero ortodiagonal y cíclico, el anticentro coincide con la intersección de las diagonales del cuadrilátero.

Demostración. Recordemos que en un cuadrilátero cíclico las $m$-alturas son concurrentes y definimos al punto de concurrencia como el anticentro, el cual tiene la propiedad de ser simétrico al circuncentro respecto a $G$, el centroide del cuadrilátero.

Sea $\square ABCD$ ortogonal y cíclico, tracemos el segmento $MP$ que pasa por el punto medio de $AB$ y la intersección de las diagonales $P$, consideremos $H = MP \cap BC$.

En un triángulo rectángulo la distancia del punto medio de la hipotenusa a los tres vértices del triángulo es la misma, por lo tanto, $\triangle AMP$ es isósceles pues $\angle DPA = \dfrac{\pi}{2}$.

Esto implica que $\angle PAM = \angle MPA = \angle HPC$.

Donde la última igualdad se debe a que los ángulos considerados son opuestos por el vértice, además $\angle ADP = \angle PCH$.

Como consecuencia de las últimas dos igualdades tenemos $\triangle APD \sim \triangle PHC$, por criterio de semejanza AA.

Entonces $\angle CHP = \angle DPA = \dfrac{\pi}{2}$, por lo tanto, $MH$ es una $m$-altura de $\square ABCD$.

De manera análoga podemos ver que las otras $m$-alturas pasan por $P$ y como todas las $m$-alturas de un cuadrilátero cíclico concurren en el anticentro entonces este coincide con $P$.

$\blacksquare$

Proposición 2. En un cuadrilátero cíclico y ortodiagonal la distancia desde el circuncentro a uno de los lados del cuadrilátero es igual a la mitad del lado opuesto.

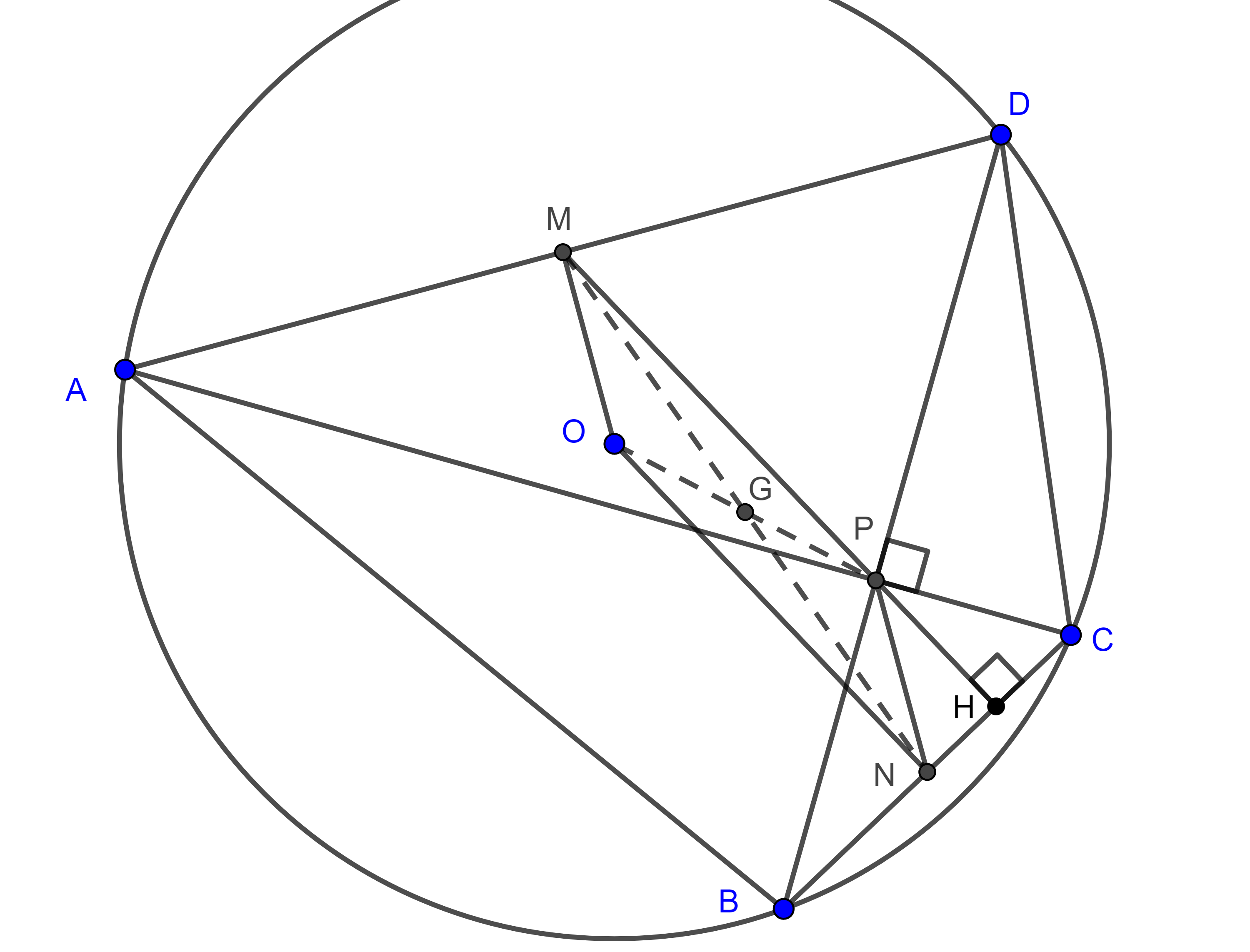
Demostración. Sea $G$ el centroide del cuadrilátero $\square ABCD$ (figura 5) y $N$ el punto medio de $BC$.

Sabemos que $G$ biseca a $MN$ y a $OP$, por lo tanto, $\square MONP$ es un paralelogramo, en consecuencia, la distancia de $O$ a $BC$ es $ON = MP = \dfrac{AD}{2}$.

Donde la primera igualdad se da porque $\square MONP$ es paralelogramo y la segunda porque $M$ es el punto medio de la hipotenusa en $\triangle APD$.

$\blacksquare$

Corolario 1. El circunradio de un cuadrilátero cíclico y ortodiagonal $\square ABCD$ con lados $a = AB$, $b = BC$, $c = CD$ y $d = AD$ cumple la siguiente igualdad, $4R^2 = a^2 + c^2 = b^2 + d^2$.

Demostración. Por la prueba de la proposición anterior sabemos que $\angle ONB = \dfrac{\pi}{2}$ (figura 5), por lo tanto podemos aplicar el teorema de Pitágoras a $\triangle ONB$.

$R^2 = OB^2 = ON^2 + BN^2 = (\dfrac{AD}{2})^2 + (\dfrac{BC}{2})^2$
$\Leftrightarrow  4R^2 = d^2 + b^2$.

De manera análoga se ve que $4R^2 = a^2 + c^2$.

$\blacksquare$

Circunferencia de Droz-Farny

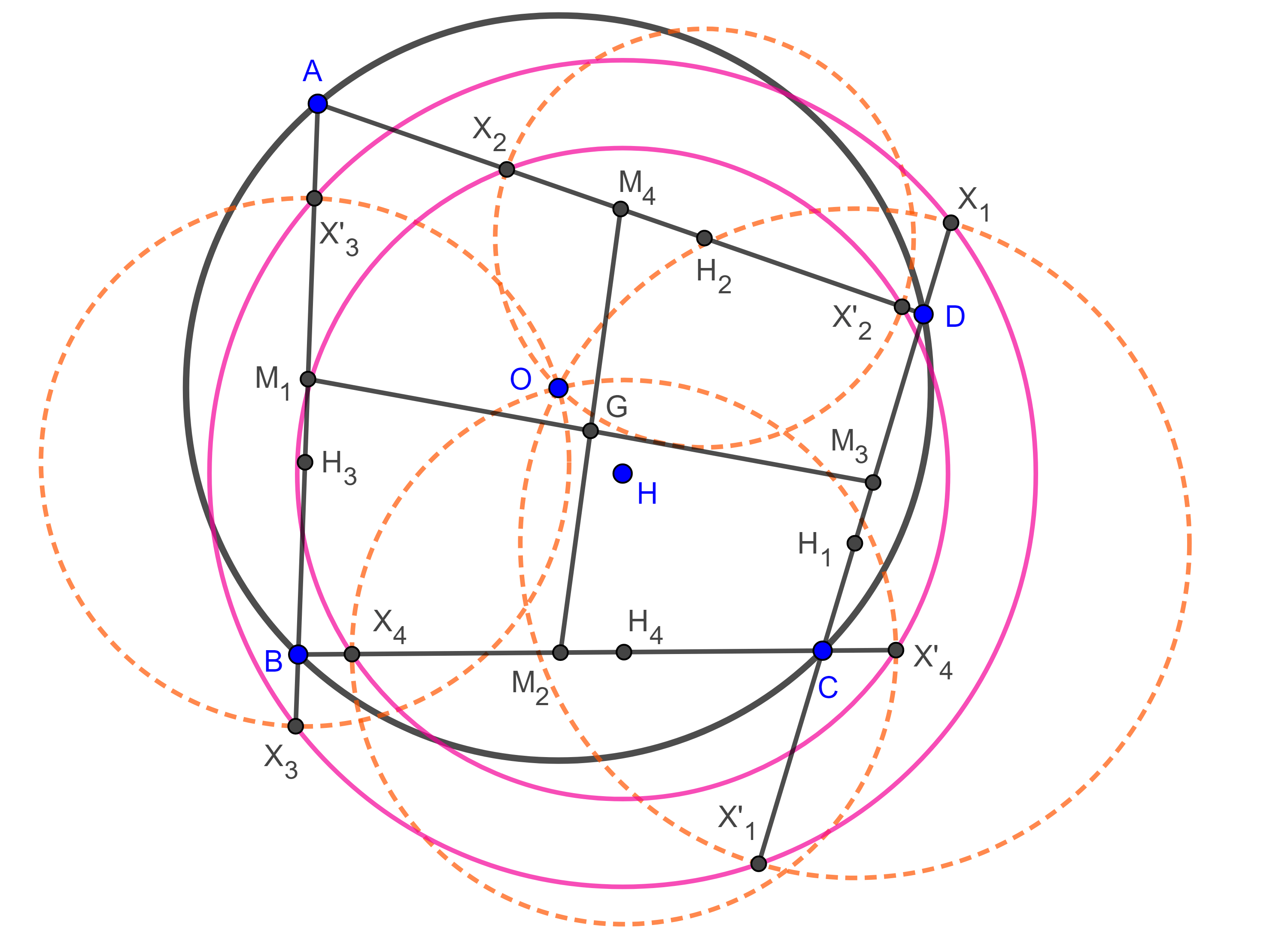
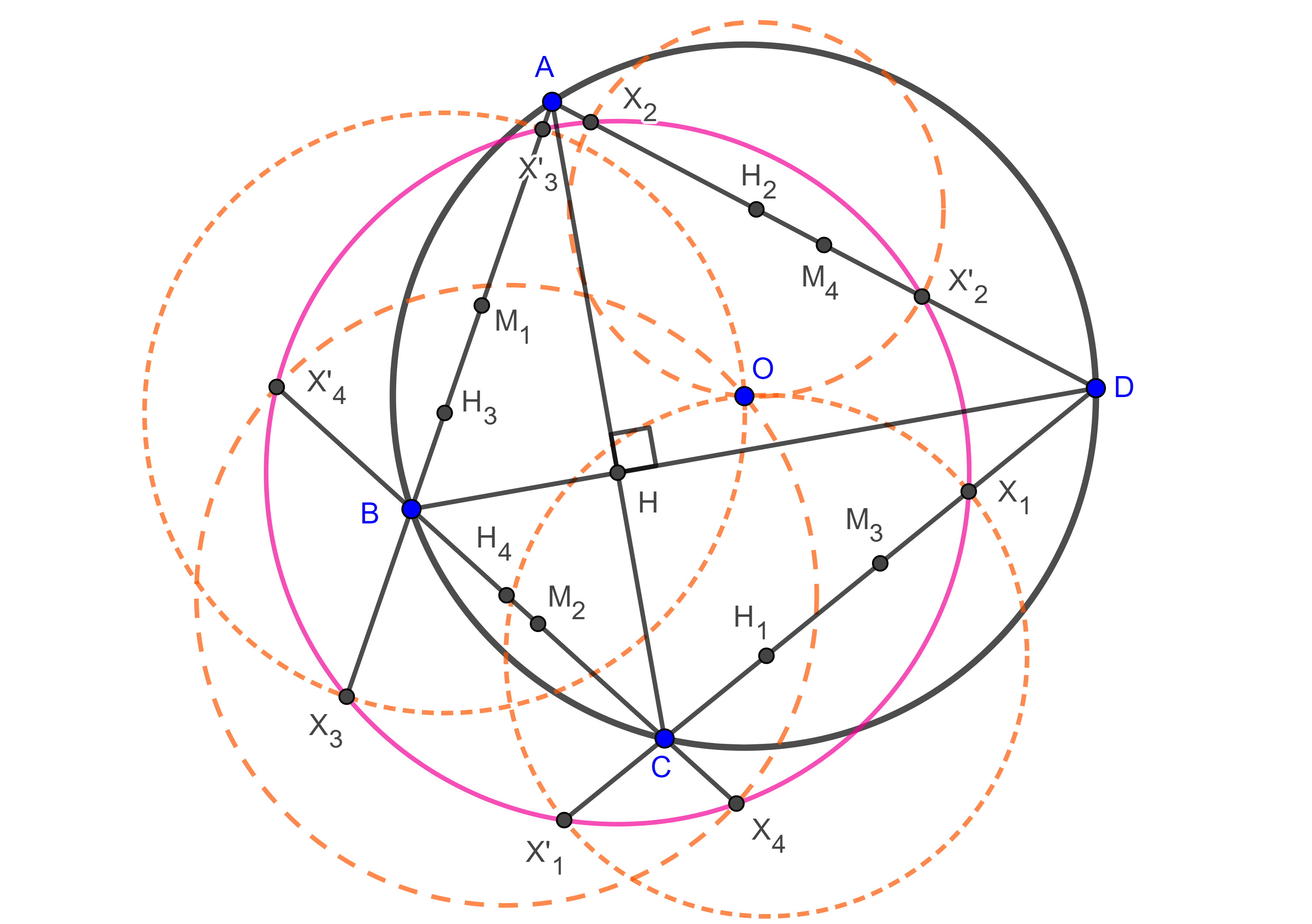
Lema 2. Sean $\square ABCD$ cíclico $O$ y $H$ el circuncentro y el anticentro respectivamente, consideremos el cuadrilátero principal órtico con vértices $H_{1} \in CD$, $H_{2} \in AD$, $H_{3} \in AB$, $H_{4} \in BC$, sean $X_{i}$, $X’_{i}$ las intersecciones de $(H_{i}, H_{i}O)$ (la circunferencia con centro en $H_{i}$ y radio $H_{i}O$) con el lado de $\square ABCD$ al que pertenece $H_{i}$. Entonces los puntos ${X_{1}, X’_{1}, X_{3}, X’_{3}}$ y los putos ${X_{2}, X’_{2}, X_{4}, X’_{4}}$ pertenecen a dos circunferencias con centro en $H$.

Demostración. Veamos que $\square X_{1}X’_{1}X_{3}X’_{3}$ es cíclico.

Dado que $HH_{1}$ es la mediatriz de $X_{1}X’_{1}$ entonces $HX_{1} = HX’_{1}$, de manera similar vemos que $HX_{3} = HX’_{3}$.

Por otra parte, como $X_{1} \in (H_{1}, H_{1}O)$, entonces $H_{1}X_{1} = H_{1}O$.

Sea $G$ el centroide del cuadrilátero $\square ABCD$ y recordemos que $G$ biseca a $OH$.

Aplicando el teorema de Pitágoras a $\triangle HH_{1}X_{1}$ y el teorema de Apolonio a la mediana $H_{1}G$ en $\triangle HH_{1}O$ obtenemos,
$HX_{1}^2 = HH_{1}^2 + H_{1}X_{1}^2 = HH_{1}^2 + H_{1}O^2$
$\begin{equation} = 2H_{1}G^2 + 2OG^2. \end{equation}$

De manera análoga calculamos
$\begin{equation} HX_{3}^2 = 2H_{3}G^2 + 2OG^2. \end{equation}$

Por el lema 1, $H_{1}$ y $H_{3}$ están en una misma circunferencia con centro en $G$ por lo tanto $H_{1}G = H_{3}G$,  de $(1)$ y $(2)$ se sigue que $HX’_{1} = HX_{1} = HX_{3} = HX’_{3}$.

Así, $X_{1}$, $X’_{1}$, $X_{3}$ y $X’_{3}$ están en una misma circunferencia con centro en $H$.

De manera análoga se ve que $X_{2}$, $X’_{2}$, $X_{4}$, $X’_{4}$ están en una misma circunferencia concéntrica con la anterior.

$\blacksquare$

Teorema 4. Sea $\square ABCD$ cíclico entonces los 8 puntos $X_{i}$, $X’_{i}$ con $i = 1, 2, 3, 4$ se encuentran en una misma circunferencia con centro en $H$, el anticentro del cuadrilátero cíclico, si y solo si $\square ABCD$ es ortodiagonal, esta es la primera circunferencia de Droz-Farny del cuadrilátero.

Demostración. Los puntos consideraos son concíclicos si y solo si las dos circunferencias a las que pertenecen tienen el mismo radio es decir $HX_{1} = HX_{2} = HX_{3} = HX_{4}$.

En la demostración del lema anterior vimos que $HX_{i}^2 = 2H_{i}G^2 + 2OG^2$.

Esto implica que $HX_{1} = HX_{2} = HX_{3} = HX_{4} \Leftrightarrow  H_{1}G = H_{2}G = H_{3}G = H_{4}G$, esto quiere decir que los vértices del cuadrilátero principal órtico de $\square ABCD$  están en una misma circunferencia con centro en $G$.

Por el teorema 3, esto ocurre si y solo si $\square ABCD$  es ortodiagonal.

$\blacksquare$

Proposición 3. Sea $\square ABCD$ cíclico y ortodiagonal entonces el radio de la primera circunferencia de Droz-Farny es igual al circunradio de $\square ABCD$.

Demostración. Por la prueba de lema 2 sabemos que
$\begin{equation} HX_{1}^2 = 2H_{1}G^2 + 2OG^2. \end{equation}$

El teorema 3 nos dice que el anticentro $H$ coincide con $P$, la intersección de las diagonales, por lo tanto $\triangle CHD$ es rectángulo (figura 7). Si $M_{3}$ es el punto medio de $CD$, la hipotenusa, entonces $M_{3}H = M_{3}C$.

Como $O$ esta en la mediatriz de $CD$, entonces $OM_3 \perp CD$.

Aplicando el teorema de Pitágoras a $\triangle OM_{3}C$ y el teorema de Apolonio a la mediana $M_{3}G$ en $\triangle OHM_{3}$ tenemos,

$\begin{equation} OC^2 = M_{3}O^2 + M_{3}C^2 = M_{3}O^2 + M_{3}H^2 = 2M_{3}G^2 + 2OG^2. \end{equation}$

Por el teorema 3, $M_{3}$ y $H_{1}$ están en una misma circunferencia con centro en $G$, por lo tanto $H_{1}G = M_{3}G$.

De $(3)$ y $(4)$ se sigue que $R = OC = HX_{1}$.

$\blacksquare$

Más adelante…

En la siguiente entrada hablaremos sobre cuadriláteros que tienen un incírculo.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

1. Muestra que de todos los cuadriláteros convexos con diagonales dadas los ortodiagonales son los de mayor área y calcula el área en función de las diagonales.
2.  Sea $\square ABCD$ un cuadrilátero convexo y $P$ la intersección de las diagonales, consideremos los circunradios $R_{1}$, $R_{2}$, $R_{3}$ y $R_{4}$ de los triángulos $\triangle APB$, $\triangle BPC$, $\triangle CPD$ y $\triangle APD$ respectivamente, demuestra que
   $i)$ $\square ABCD$ es ortodiagonal si y solo si $R_{1}^2 + R_{3}^2 = R_{2}^2 + R_{4}^2$
   $ii)$ $\square ABCD$ es ortodiagonal si y solo si los circuncentros de los triángulos $\triangle APB$, $\triangle BPC$, $\triangle CPD$ y $\triangle APD$ son los puntos medios de los lados del cuadrilátero.
3. Sea $\square ABCD$ un cuadrilátero convexo y $P$ la intersección de las diagonales, considera las alturas $h_{1}$, $h_{2}$, $h_{3}$ y $h_{4}$, de los triángulos $\triangle APB$, $\triangle BPC$, $\triangle CPD$ y $\triangle APD$ trazadas desde $P$, muestra que $\square ABCD$ es ortodiagonal si y solo si $\dfrac{1}{h_{1}^2} + \dfrac{1}{h_{3}^2} = \dfrac{1}{h_{2}^2} + \dfrac{1}{h_{4}^2}$.
4. Sean $\square ABCD$ un cuadrilátero convexo, $P$ la intersección de las diagonales, $P_{1}$, $P_{2}$, $P_{3}$ y $P_{4}$ las proyecciones trazadas desde $P$ a los lados $AB$, $BC$, $CD$ y $AD$ respectivamente, y considera los puntos $P’_{i}$ con $i = 1, 2, 3, 4$ como las intersecciones de $PP_{i}$ con el lado opuesto al que pertenece $P_{i}$ prueba que
   $i)$ $\square ABCD$ es ortodiagonal si y solo si $\angle CBP + \angle PCB + \angle PAD + \angle ADP = \pi$
   $ii)$ $\square ABCD$ es ortodiagonal si y solo si $\square P_{1}P_{2}P_{3}P_{4}$ es cíclico.
   $iii)$ $\square ABCD$ es ortodiagonal si y solo si los 8 puntos $P_{i}$, $P’_{i}$ con $i = 1, 2, 3, 4$ son cíclicos, a esta circunferencia se le conoce como segunda circunferencia de los ocho puntos del cuadrilátero ortodiagonal.
   $iv)$ La primera y la segunda circunferencias de los ocho puntos de un cuadrilátero ortodiagonal son la misma si y solo si el cuadrilátero es cíclico.

5. Muestra que un cuadrilátero convexo $\square ABCD$ es ortodiagonal si y solo si el cuadrilátero $\square P’_{1}P’_{2}P’_{3}P’_{4}$, definido en el ejercicio anterior (figura 8), es un rectángulo cuyos lados son paralelos a las diagonales de $\square ABCD$.
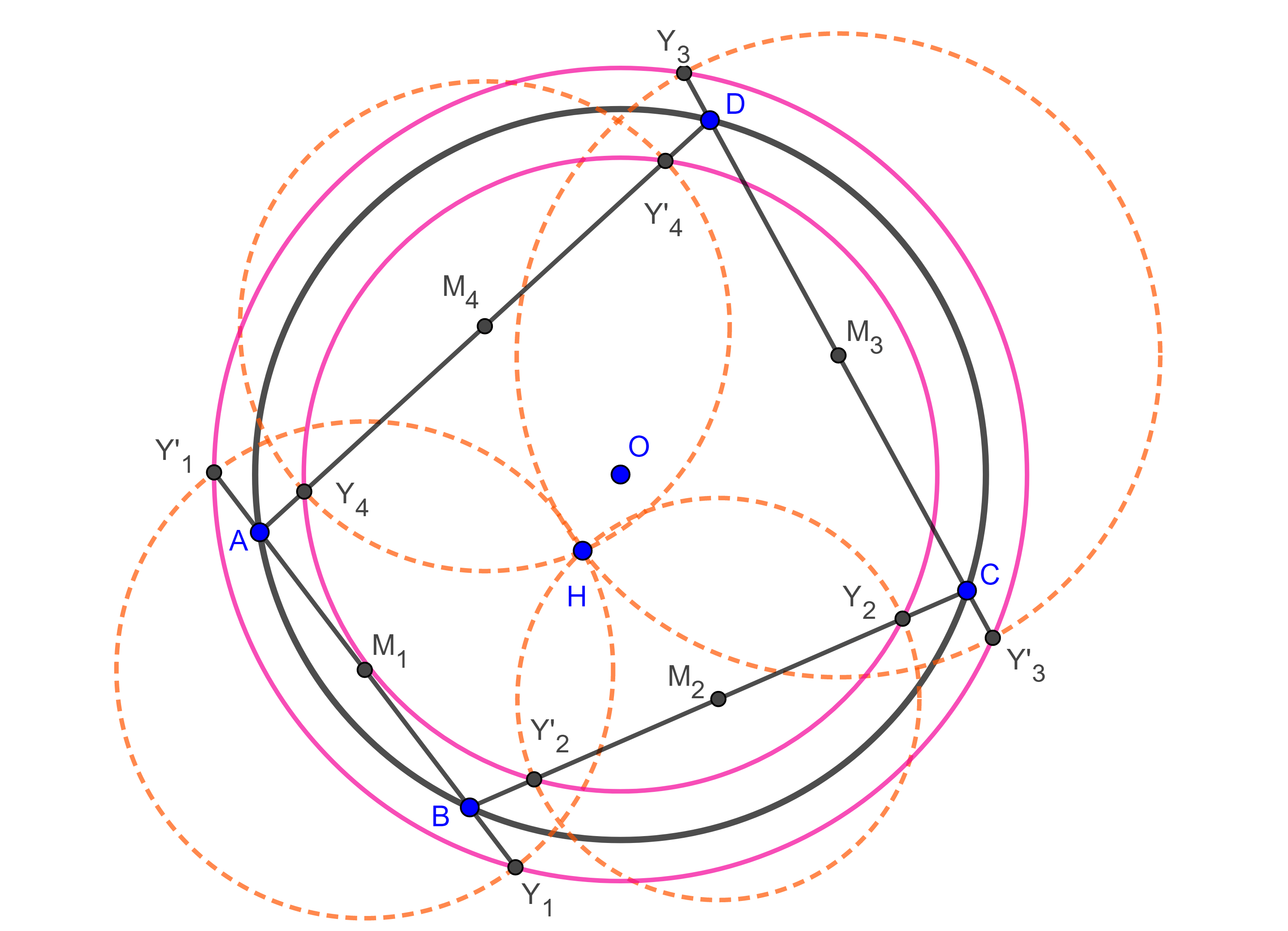
6. Sean $\square ABCD$ cíclico, $O$ el circuncentro, $H$ el anticentro y considera los puntos medios $M_{i}$ con $i = 1, 2, 3, 4$ del cuadrilátero (figura 9), define $Y_{i}$, $Y’_{i}$ como las intersecciones de $(M_{i}, M_{i}H)$ (la circunferencia con centro en $M_{i}$ y radio $M_{i}H$) con el lado de $\square ABCD$ al que biseca $M_{i}$.
   $i)$ Muestra que los puntos ${Y_{1}, Y’_{1}, Y_{3}, Y’_{3}}$ y los putos ${Y_{2}, Y’_{2}, Y_{4}, Y’_{4}}$ están en dos circunferencias con centro en $O$
   $ii)$ Dichas circunferencias son la misma si y solo si $\square ABCD$ es ortodiagonal, esta es la segunda circunferencia de Droz-Farny del cuadrilátero.

Entradas relacionadas

• Ir a Geometría Moderna I.
• Entrada anterior del curso: Cuadrilátero cíclico.
• Siguiente entrada del curso: Cuadrilátero circunscrito.
• Otros cursos.

Fuentes

• Altshiller, N., College Geometry. New York: Dover, 2007, pp 136-138.
• Mammana, Maria Flavia; Micale, Biagio; Pennisi, Mario., The Droz-Farny Circles of a Convex Quadrilateral, Forum Geometricorum, (2011), 11, pp 109–119.
• Josefsson, Martin., Characterizations of Orthodiagonal Quadrilaterals, Forum Geometricorum, (2012), 12, pp 13–25.
• Wikipedia

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»