Introducción

En una entrada anterior, acerca de funciones continuas, mencionamos dos teoremas fundamentales que estas funciones satisfacen: el teorema del valor intermedio y el teorema del valor extremo. Ya hablamos acerca del teorema del valor intermedio en una entrada anterior. El objetivo de esta entrada es mencionar aplicaciones del teorema del valor extremo.

Como recordatorio, el teorema del valor extremo o teorema de los valores extremos nos dice que si una función $f(x)$ es continua en un intervalo cerrado $[a, b]$, entonces existen valores $c$ y $d$ en $[a, b]$ tales que $f(c) \leq f(x) \leq f(d)$ para toda $x$ en el intervalo $[a, b]$.

En otras palabras, lo que nos dice el teorema es que si una función es continua en un intervalo cerrado, tenemos que la función debe alcanzar un valor máximo y un valor mínimo dentro del intervalo.

Dos teoremas para funciones derivables

Aprovecharemos para mencionar dos teoremas importantes que se ocuparán más adelante. Las demostraciones de dichos teoremas tienen que ver con la aplicación del teorema del valor extremo, estos teoremas son el teorema de Rolle y el teorema del valor medio (no confundir con el teorema del valor intermedio).

Teorema de Rolle. Sean $a<b$ reales y $f:[a,b]\to\mathbb{R}$ una función continua en el intervalo $[a, b]$ y derivable en $(a, b)$. Se tiene que si $f(a)=f(b)$, entonces existe $c$ en $(a, b)$ tal que $f^\prime(c)=0$.

Sugerencia pre-demostración. Por el teorema del valor extremo, la función debe alcanzar un máximo y un mínimo en el intervalo. Divide en casos de acuerdo a dónde están estos valores, si en los extremos o no.

Demostración: Como $f(x)$ es una función continua en $[a, b]$, por el teorema del valor extremo tenemos que $f(x)$ alcanza un valor máximo y un valor mínimo en el intervalo $[a, b]$. Tenemos entonces los siguientes casos.

• Caso i: Si el valor máximo y mínimo se encuentran en los extremos del intervalo, tenemos que la función $f(x)$ tiene que ser constante dado que $f(a)=f(b)$. y se tiene que $f^\prime(c)=0$ para todo $c$ en $[a, b]$.

• Caso ii: Si el valor mínimo o máximo no están en los extremos. Sean $c_1$ y $c_2$ en $(a, b)$, los valores en los que la función alcanza su mínimo y máximo respectivamente. Alguno de estos no está en los extremos. Como $f(x)$ es derivable en $(a, b)$, tenemos que también va a ser derivable en alguno de los puntos $c_1$ y $c_2$, teniendo que $f^\prime(c_1)=0$ o $f^\prime(c_2)=0$, así que basta con tomar $c=c_1$ o $c=c_2$.

$\square$

Teorema del valor medio. Sean $a<b$ reales y $f:[a,b]\to\mathbb{R}$ una función continua en $[a, b]$ y diferenciable en $(a, b)$. Entonces existe un número $c$ en $(a, b)$ tal que

$\frac{f(b)-f(a)}{b-a}=f^\prime(c)$.

Demostración: Consideremos la siguiente función auxiliar:

$g(x)=(f(b)-f(a))x-(b-a)f(x)$

Tenemos que $g(x)$ es continua en $[a, b]$ y además es derivable en $(a,b)$. La derivada de $g(x)$ está dada por

$g^\prime(x)=f(b)-f(a)-(b-a)f^\prime(x)$

Como $g(x)$ es continua en $[a, b]$, tenemos que por el teorema del valor extremo, la función alcanza un máximo y un mínimo en el intervalo $[a, b]$. Haciendo las cuentas, $g(a)=g(b)$, de modo que si el máximo y mínimo ocurren en los extremos, entonces $g$ es constante y toda $c\in (a,b)$ satisface $g'(c)=0$

En otro caso, sea $c\in(a, b)$ el valor en donde $g(x)$ alcanza su mínimo o su máximo. Tenemos que $g^\prime(c)=0$.

Así, como $g^\prime(c)=f(b)-f(a)-(b-a)f^\prime(c)$, tenemos que:

$0=f(b)-f(a)-(b-a)f^\prime(c)$

$(b-a)f^\prime(c)=f(b)-f(a)$

$f^\prime(c)=\frac{f(b)-f(a)}{b-a}$

$\square$

Alternativamente, en la función anterior pudimos haber aplicado el teorema de Rolle directamente a la función $g$. En las siguientes entradas veremos aplicaciones de estos resultados a problemas concretos.

Aplicación del teorema del valor extremo a un problema

Problema. Se tiene un circulo de radio $r$, y una tangente $L$ que pasa por un punto $P$ de la circunferencia. De un punto cualquiera $R$ en la circunferencia se traza una paralela a $L$ que corta a la circunferencia en $Q$. Determina el área máxima que puede tener el triángulo $PQR$.

Sugerencia pre-solución. Antes que nada, haz una figura. Usa el teorema del valor extremo para asegurar la existencia del valor máximo. Para ello, necesitarás construir una función continua cuyo valor sea el área buscada. Puedes usar argumentos de simetría para conjeturar cuándo se alcanza el valor máximo.

Solución. Hacemos el siguiente diagrama para entender mejor el problema.

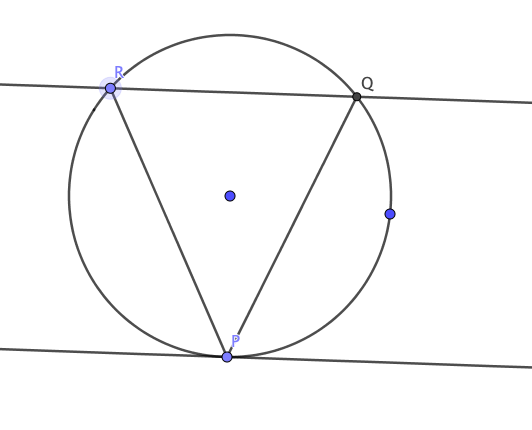
Fijémonos que las condiciones de la altura y la base del triángulo $PQR$ se pueden describir mediante la siguiente figura:

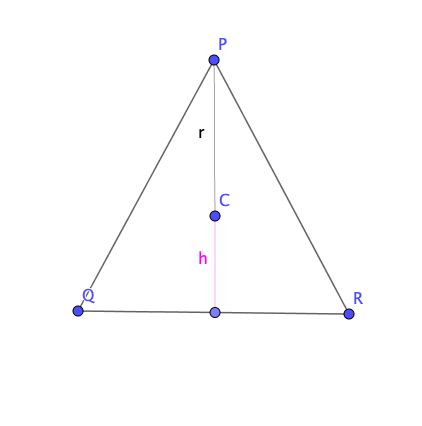
Notemos que la altura del triángulo está dada por $r+h$, donde $h$ puede variar entre $-r$ y $r$. Este dibujo también nos es de ayuda para determinar el valor de la base. Por el teorema de Pitágoras y sabiendo que la distancia del centro $C$ a los puntos $R$ y $Q$ es igual a $r$, tenemos que la base del triángulo es igual a $2\sqrt{r^2-h^2}$.

Así, el área del triángulo está dada por $(\sqrt{r^2-h^2})(r+h)$, pero como $h$ varía, nos conviene ver el área en función de $h$.

$A(h)=\sqrt{r^2-h^2}(r+h),$

La función $A(h)$ es una función continua en el intervalo $[-r, r]$.

Notemos que cuando $h$ toma los valores de $-r$ y $r$, el valor del área es nulo, es decir que en estos valores alcanza el mínimo, lo cual quiere decir que por el teorema del valor extremo, el valor máximo lo alcanza en algún valor en $(-r, r)$.

Si derivamos la función $A(h)$, tenemos

$A^\prime(h)=\frac{r^2-rh-2h^2}{\sqrt{r^2-h^2}}.$

Como sabemos que hay un máximo en el intervalo $(-r, r)$ y la derivada en este punto máximo debe ser igual a cero, hacemos $A^\prime(h)=0$.

Así,

$\frac{r^2-rh-2h^2}{\sqrt{r^2-h^2}}=0.$

Resolviendo la ecuación tenemos que

$h=\frac{r}{2}.$

Así, el área máxima del triángulo $PQR$ es $$A=\sqrt{r^2-\left(\frac{r}{2}\right)^2}\left(r+\frac{r}{2}\right)=\frac{3\sqrt{3}r^2}{4}.$$

$\square$

Más ejemplos

Se pueden encontrar más problemas de aplicación del teorema del vaalor extremo en la Sección 6.4 del libro Problem Solving through Problems de Loren Larson.