Introducción
En esta entrada voy a platicar de una forma en la que se puede plantear un modelo de epidemia básico usando álgebra lineal. Es un modelo bastante simple, sin embargo a partir de él se pueden verificar varias de las lecciones que hemos estado aprendiendo durante la crisis del coronavirus. A grandes rasgos, haremos algunas suposiciones razonables para plantear una epidemia como un modelo de Markov.
Ya que hagamos esto, estudiaremos dos escenarios posibles: en el que la gente sale de sus casas y en el que la gente se queda en sus casas. Para ello usaremos las librerías NumPy y Matplotlib de Python para hacer las cuentas y generar bonitas gráficas como la siguiente:
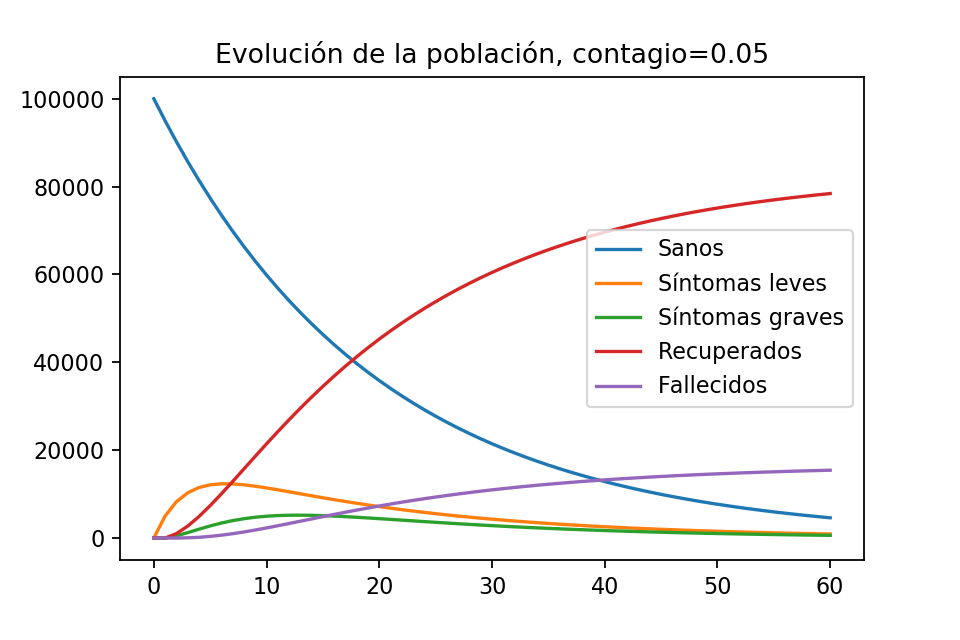
En particular, veremos que incluso de este modelo simple se notan contrastes importantes en ambos escenarios. En particular, se puede deducir la importancia de #QuédateEnCasa para retrasar el contagio y no saturar los sistemas de salud.
Advertencia: De ninguna forma esta entrada pretende modelar, específicamente, la evolución del coronavirus. Para ello hay expertos trabajando en el tema, y están usando modelos mucho más sofisticados que el que platicaré. Esta entrada es, en todo caso, una introducción al tema y ayuda a explicar, poco a poco, algunos de los argumentos que se usan en modelación matemática de epidemias.
Suposiciones y modelo tipo Markov
Comenzemos a plantear el modelo de epidemia básico. Pensemos en una enfermedad imaginaria, que se llama «Imagivid» y en un territorio imaginario que se llama «Imagilandia», donde la población inicial es de $100,000$ habitantes sanos, en el día $0$.
Vamos a pensar que una persona puede estar en alguno de los siguientes cinco estados:
- Sano
- Síntomas leves
- Síntomas graves
- Recuperado
- Fallecido
Para cada día $n$, consideremos el vector $$X(n)=(s(n),l(n),g(n),r(n),f(n))$$ de $5$ entradas cuyas entradas son los sanos, de síntomas leves, de síntomas graves, recuperados y fallecidos al día $n$. Por ejemplo al día $0$ dijimos que todos están sanos, así que $X(0)=(100000,0,0,0,0)$.
Haremos las siguientes suposiciones de cómo se pasa de un estado a otro
- Los únicos fallecidos del periodo de tiempo que tendremos son por Imagivid. Sólo se puede fallecer de ello tras tener síntomas graves. Si alguien tiene síntomas graves, entonces tiene cierta probabilidad $g_f$ de fallecer al día siguiente, $g_r$ de recuperarse y por lo tanto $1-g_r-g_f$ de quedarse como enfermo grave.
- Imagivid se contagia de persona a persona, y de un día a otro una persona tiene probabilidad $s_l$ de pasar de estar sana a tener síntomas leves. No se puede pasar directamente a tener síntomas graves, recuperarse o morir. De modo que se queda sana de un día a otro con probabilidad $1-s_l$
- Si una persona tiene síntomas leves, tiene probabilidad $l_g$ de pasar a tener síntomas graves y $l_r$ de pasar a recuperarse. Por lo tanto, tiene probabilidad $1-l_g-l_r$ de quedarse con síntomas leves.
- Una persona que se recupera desarrolla inmunidad a Imagivid, así que se queda en ese estado.
- Una persona que fallece, se queda en ese estado.
En otras palabras, tenemos el siguiente diagrama de cómo se pasa de tener un estado a otro, en donde los números en las flechas muestran la probabilidad de pasar de un estado a otro:
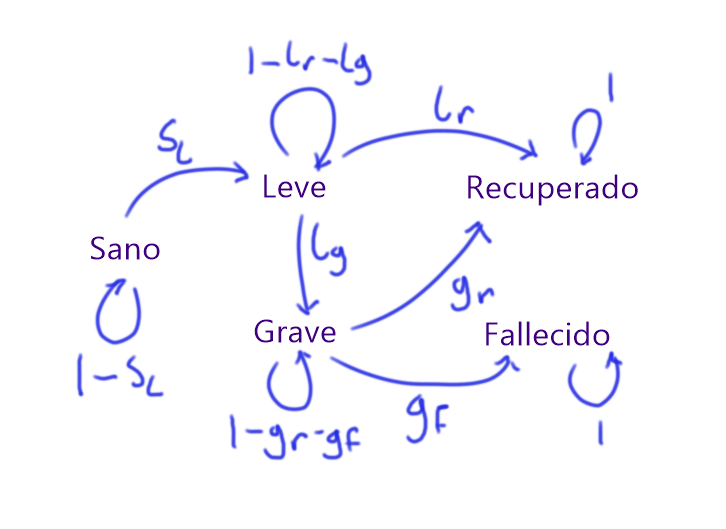
En lenguaje técnico, estamos modelando a la epidemia como un proceso de Markov. Sin embargo, no es necesario entender toda la teoría de procesos de Markov para entender lo que sigue, pues la idea es bastante intuitiva.
Con estos números y suposiciones, podemos entender, en valor esperado, cómo será el vector de población $$X(n+1)=(s(n+1), l(n+1), g(n+1), r(n+1), f(n+1))$$ si sabemos cómo es el vector $$X(n)=(s(n), l(n), g(n), r(n), f(n)).$$ Por ejemplo, podemos esperar que la cantidad de recuperados al día $n+1$ sea $$r(n+1)=l_r \cdot l(n)+ g_r \cdot g(n) + 1 \cdot r(n),$$ pues de los de síntomas leves del día $n$ habrá una proporción $l_r$ de ellos que se recuperen, de los graves del día $n$ habrá una proporción $g_r$ de ellos que se recuperen, y todos los recuperados del día $n$ se quedan recuperados. De esta forma, obtenemos el siguiente sistema de ecuaciones de lo que podemos esperar:
\begin{align*}
s(n+1)&=(1-s_l) \cdot s(n)\\
l(n+1)&=s_l \cdot s(n) + (1-l_r-l_g) \cdot l(n)\\
g(n+1)&= l_g \cdot l(n) + (1-g_r-g_f) \cdot g(n)\\
r(n+1)&=l_r \cdot l(n) + g_r \cdot g(n) + 1 \cdot r(n)\\
f(n+1)&=g_f \cdot g(n) + 1 \cdot f(n),
\end{align*}
Este sistema de ecuaciones se puede escribir de una forma mucho más compacta. Si definimos la matriz $$A=\begin{pmatrix} 1-s_l & 0 & 0 & 0 & 0 \\s_l & 1-l_r-l_g & 0 & 0 & 0 \\0 & l_g & 1-g_r-g_f & 0 & 0 \\ 0 & l_r & g_r & 1 & 0\\ 0 & 0 & g_f & 0 & 1 \end{pmatrix},$$ las ecuaciones anteriores se pueden abreviar simplemente a $$X(n+1)=AX(n).$$
De esta forma, si queremos entender qué esperar del día $n$, basta hacer la multiplicación matricial $X(n)=A^n X(0)$.
Un ejemplo concreto en Python
El modelo de epidemia básico que planteamos arriba depende de cinco parámetros:
- $s_l$, la probabilidad de pasar de estar sano a tener síntomas leves,
- $l_g$, la probabilidad de pasar de tener síntomas leves a graves,
- $l_r$, la probabilidad de pasar de tener síntomas leves a recuperarse,
- $g_r$, la probabilidad de pasar de tener síntomas graves a recuperarse y
- $g_f$, la probabilidad de pasar de tener síntomas graves, a fallecer.
Hagamos un ejemplo concreto, en el que estos parámetros para Imagivid son los siguientes: $s_l=0.30$, $l_g=0.10$, $l_r=0.20$, $g_r=0.10$ y $g_f=0.10$. En «la vida real», para hacer una modelación correcta se tienen que estimar estos parámetros de lo que ya se sepa de la enfermedad.
Si ponemos estos valores, la matriz que obtenemos es la siguiente:
$$A=\begin{pmatrix} 0.7 & 0 & 0 & 0 & 0 \\0.3 & 0.7 & 0 & 0 & 0 \\0 & 0.1 & 0.8 & 0 & 0 \\ 0 & 0.2 & 0.1 & 1 & 0\\ 0 & 0 & 0.1 & 0 & 1 \end{pmatrix}.$$
Vamos a usar la fórmula que obtuvimos en la sección anterior para entender cómo va evolucionando la epidemia de Imagivid. Para no hacer las cuentas a mano, usaremos Python. Trabajaremos con Python 3 y usaremos Numpy (para las cuentas de matrices) y Matplotlib (para visualizar gráficas). En el siguiente código definimos la población inicial, los parámetros de transición y la matriz de la sección anterior.
import numpy as np
import matplotlib.pyplot as plt
# En cada momento tendremos un vector
# de la distribución de la población
# (sanos, sintomas leves, sintomas graves,
# recuperados, fallecidos)
# Población inicial
x_0=(100000,0,0,0,0)
# Definimos las probabilidades de
# transición
S_L = 0.30
L_G = 0.10
L_R = 0.20
G_R = 0.10
G_F = 0.10
# Definimos la matriz A
A=np.array([[1-S_L,0,0,0,0],[S_L,1-L_G-L_R,0,0,0],[0,L_G,1-G_R-G_F,0,0],[0,L_R,G_R,1,0],[0,0,G_F,0,1]])Vamos a estudiar la evolución de Imagivid por 60 días. Por ello, vamos a hacer un bucle en Python que calcule cómo son los vectores de población de todos estos 60 días. Para empezar a entender cómo funciona nuestro modelo de epidemia, también pediremos que muestre los valores para los días 1, 2 y 3.
# Encontramos la evolución de la
# epidemia los primeros 60 días
evolution=[x_0]
for j in range(60):
evolution.append(np.matmul(A,evolution[-1]))
# Mostramos lo que pasa los primeros
# 3 días
for j in range(1,4):
print(evolution[j])Los valores que obtenemos son
\begin{align*}
X_1 &= (70000,30000,0,0,0)\\
X_2 &= (49000, 42000, 3000, 6000)\\
X_3 &= (34300, 44100, 6600, 14700, 300).
\end{align*}
Esto nos dice que al primer día hay $70000$ sanos y $30000$ con síntomas leves. En los primeros dos días no hay fallecidos, pues de acuerdo a nuestro modelo de epidemia un habitante primero debe presentar síntomas leves, luego graves y luego ya tal vez fallece. Al día 3 el modelo predice $300$ fallecidos.
Esto son sólo tres días, pero sería bueno poder entender qué sucede en todo el periodo de 60 días. Para ello, vamos a pedir a Python que nos muestre una gráfica de cómo evoluciona la población a través del tiempo. Para ello hacemos lo siguiente
# Hacemos gráfica para mostrar la evolución de todo el tiempo
plt.plot([j[0] for j in evolution], label="Sanos")
plt.plot([j[1] for j in evolution], label="Síntomas leves")
plt.plot([j[2] for j in evolution], label="Síntomas graves")
plt.plot([j[3] for j in evolution], label="Recuperados")
plt.plot([j[4] for j in evolution], label="Fallecidos")
plt.title("Evolución de la población, contagio=0.30")
plt.legend()
plt.show()Obtenemos la siguiente imagen
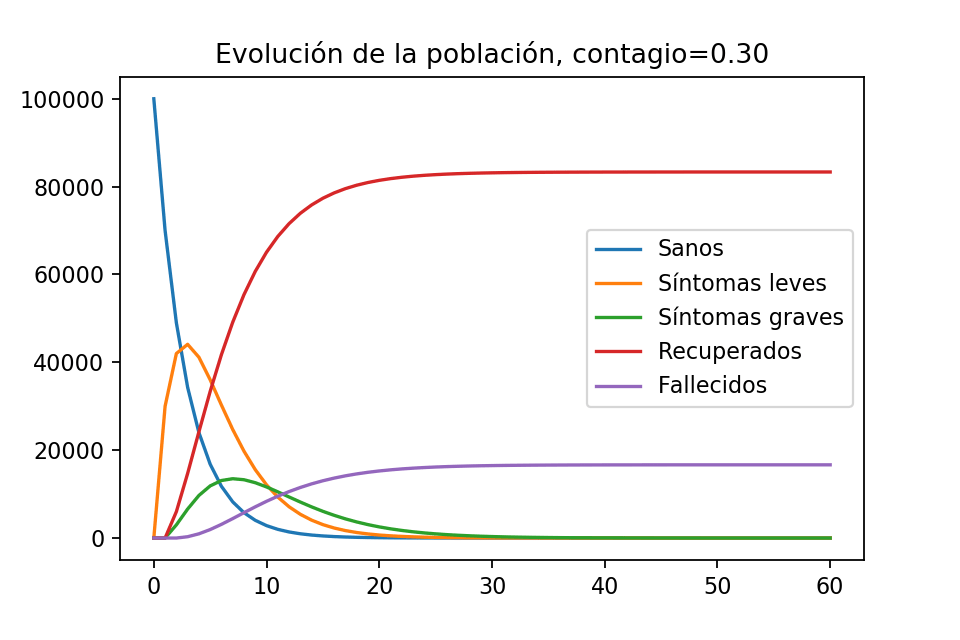
La gráfica tiene sentido es de esperarse que, tras cierta cantidad de tiempo, ya sólo haya habitantes recuperados y fallecidos. Notemos que hay un momento el el que la población con síntomas leves es de aproximadamente $40,000$ habitantes y que la población con síntomas graves llega a ser, en algún momento, como de $12,000$ habitantes.
¿Qué sucede al final de nuestro periodo de estudio? Si le pedimos a Python que nos de las últimas dos entradas del vector de población al día $60$,
#Mostramos recuperados y fallecidos al último día
print(evolution[-1][3])
print(evolution[-1][4])obtenemos $\sim 83,333$ recuperados y $\sim 16,666$ fallecidos al día $60$, de modo que en este escenario la epidemia cobró $16,666$ vidas de Imagilandia. De hecho una observación muy importante, viendo la gráfica, es que ya se tenía prácticamente esta cantidad de víctimas desde el día 30.
Disminuir la tasa de infección para retrasar la epidemia
Antes de que sucediera la tragedia, las autoridades de Imagilandia estudiaron el modelo de epidemia que acabamos de mencionar y se dieron cuenta de que tenían que tomar una acción inmediata para mejorar la situación. Decidieron que una cosa muy importante para que la situación mejorara era pedirle a la gente que se quedara en sus casas lo más posible, pues con ello se disminuiría la tasa de contagio. Para ello sacaron la campaña #QuédateEnCasa. Las personas hicieron caso.
Habiendo más personas sanas y enfermas en su propia casa, ahora ni los enfermos pueden contagiar a sanos, ni los sanos estar expuestos a enfermos. Así, una persona sana ahora tiene menor probabilidad de estar enferma al día siguiente. Supongamos que $s_l$ pasa de ser $0.30$ a ahora ser $0.05$. De esta forma, ahora tenemos una nueva matriz que ayuda a calcular la evolución de la pandemia:
$$A=\begin{pmatrix} 0.95 & 0 & 0 & 0 & 0 \\0.05 & 0.7 & 0 & 0 & 0 \\0 & 0.1 & 0.8 & 0 & 0 \\ 0 & 0.2 & 0.1 & 1 & 0\\ 0 & 0 & 0.1 & 0 & 1 \end{pmatrix}.$$
Vamos a pedirle de nuevo a Python que haga las cuentas para los primeros 60 días bajo las suposiciones de nuestro modelo de epidemia y que nos muestre una gráfica de la evolución de la población.
# Definimos las probabilidades de transición, que son iguales salvo que ahora la tasa de contagio es menor, y por lo tanto S_L es menor
S_L = 0.05
L_G = 0.10
L_R = 0.20
G_R = 0.10
G_F = 0.10
# Definimos la matriz A
A=np.array([[1-S_L,0,0,0,0],[S_L,1-L_G-L_R,0,0,0],[0,L_G,1-G_R-G_F,0,0],[0,L_R,G_R,1,0],[0,0,G_F,0,1]])
evolution2=[x_0]
for j in range(60):
evolution2.append(np.matmul(A,evolution2[-1]))
plt.plot([j[0] for j in evolution2], label="Sanos")
plt.plot([j[1] for j in evolution2], label="Síntomas leves")
plt.plot([j[2] for j in evolution2], label="Síntomas graves")
plt.plot([j[3] for j in evolution2], label="Recuperados")
plt.plot([j[4] for j in evolution2], label="Fallecidos")
plt.title("Evolución de la población, contagio=0.05")
plt.legend()
plt.show()La gráfica que obtenemos es la siguiente:
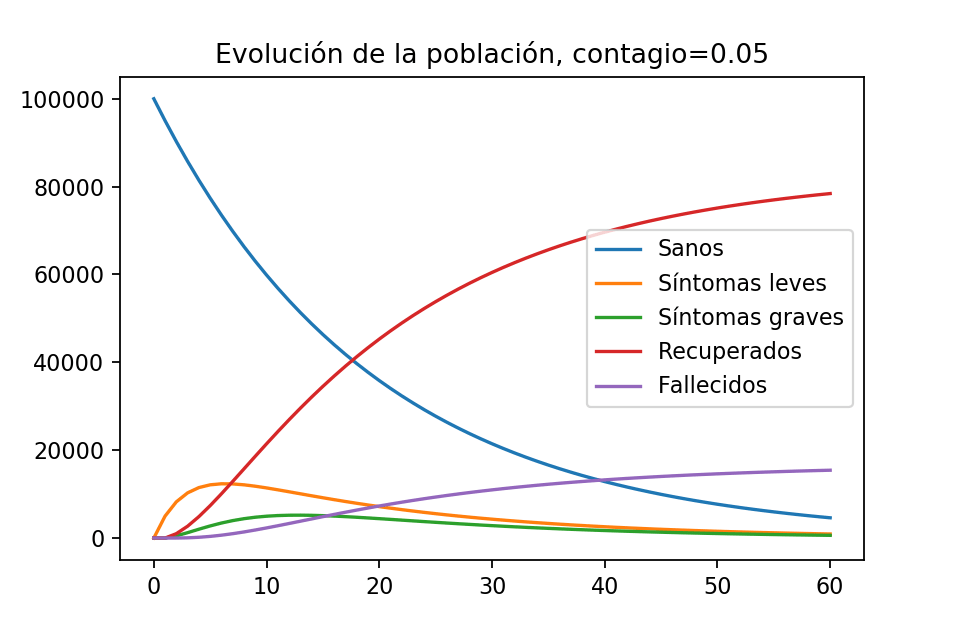
Una cosa fantástica en este escenario es que nunca hay muchas personas enfermas simultáneamente. En el peor día, parece haber como $12,000$ personas enfermas con síntomas leves, y parece que nunca hay más de $6000$ personas con síntomas graves. ¿Qué sucede con la mortalidad? Si le pedimos a Python que nos diga el número de habitantes recuperados y fallecidos al día 60,
print(evolution2[-1][3])
print(evolution2[-1][4])obtenemos $\sim 78,419$ recuperados y $\sim 15,438$ fallecidos. Esto es ligeramente mejor que en la situación anterior, en donde había $\sim 16,000$ fallecidos. Donde sí hay una diferencia es en lo que sucede al día $30$. Si pedimos a Python que nos muestre la cantidad de fallecidos al día $30$ en ambos escenarios obtenemos lo siguiente.
print(evolution[30][4])
print(evolution2[30][4])En el primer escenario, en el que la gente no se queda en casa, al día $30$ tenemos $\sim 16,493$ fallecidos, que es prácticamente ya todos los que habrá. Cuando la gente se queda en casa, al día $30$ sólo hay $\sim 10,963$, una buena parte menos.
Esto parece estar mejor, sin embargo, el tiempo va a seguir pasando, y de todas formas llegaremos al día $60$, en donde ambos escenarios son muy parecidos ¿Por qué entonces todo el esfuerzo de pedirle a la gente que se quede en casa, si la diferencia es mínima? Porque el tiempo es oro.
La carrera contra el tiempo
Hay muchas razones por las cuales es conveniente retrasar la epidemia de Imagivid en Imagilandia, aunque el modelo sencillo que mostramos arriba muestre qe a los 60 días parecería que habrá la misma cantidad de fallecidos.
Primero, es importante retrasar los contagios pues existe la posibilidad de que los científicos de Imagilandia entiendan mejor a Imagivid y, por ejemplo, desarrollen una vacuna o un tratamiento. ¿Qué sucedería si los científicos encuentran una cura al día $30$? En el primer escenario sólo se salvan unas $\sim 150$ vidas, pero en el segundo escenario se salvan unas $\sim 4,500$, osea, unas $\sim 4350$ más. En otras palabras, en el primer escenario el desarrollo científico llega demasiado tarde.
Segundo, también es importante retrasar la epidemia pues permite tener el número de casos simultáneos bajo control. Esto ya lo discutimos un poco arriba, pero pidamos a Python una gráfica más, para poder discutirlo de manera más clara. Supondremos, además, que Imagilandia cuenta con solamente $6000$ camas de hospital en donde se pueden tratar los casos severos de Imagivid, y le pediremos a Python que ponga esto como una línea horizontal.
plt.plot([j[1] for j in evolution2], color="green", linestyle=":", label="Leves, Contagio=0.05")
plt.plot([j[2] for j in evolution2], color="green", label="Severos, Contagio=0.05")
plt.plot([j[1] for j in evolution], color="red", linestyle=":", label="Severos, Contagio=0.30")
plt.plot([j[2] for j in evolution], color="red", label="Severos, Contagio=0.30")
plt.hlines(6000,0,60, color="black", label="Capacidad sistema salud")
plt.title("Enfermos a través del tiempo")
plt.legend()
plt.plot()Obtenemos la siguiente gráfica:
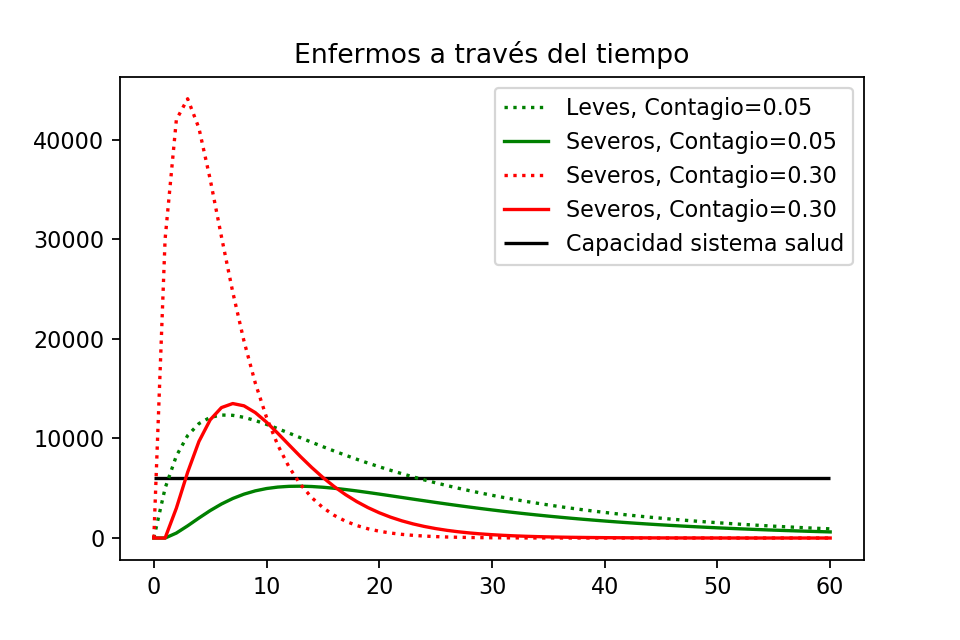
Cuando la gente sí se queda en sus casas y la tasa de contagio es baja (en verde), siempre hay suficiente espacio en el sistema de salud para tratar a a los enfermos graves.
Cuando la gente no se queda en sus casas y la tasa de contagio es alta (en rojo), notemos que los casos severos sobrepasan al sistema de salud. Aproximadamente entre los días $3$ y $15$ se tienen muchos enfermos graves que no podrán ser atendidos correctamente. Por ejemplo, al día 9 hay aproximadamente $\sim 6000$ enfermos graves por encima de la capacidad del sistema de salud. Sin atención médica, probablemente en vez de que sólo fallezcan el $10\%$ de ellos (según nuestro modelo), fallecerán casi todos, dando $5400$ víctimas más que no hemos contado.
De esta forma, siguiendo los consejos de quedarse en casa, la población de Imagilandia puede salvar, potencialmente, $\sim 4350$ personas por la vacuna y $\sim 5400$ personas por evitar saturar el sistema de salud, osea, salvar unas $\sim 9750$ vidas. Para ello es necesario que las autoridades hagan el llamado a quedarse, y que la población de Imagilandia haga caso. De aquí la importancia del #QuédateEnCasa.
Más contenido
Todo el código de Python del modelo lo corrí en una libreta de Jupyter. Puedes ver una versión en PDF de todo el código a continuación.
Si quieres el archivo de Jupyter para jugar con el modelo, puedes obtenerlo en el GitHub del proyecto: https://github.com/leomtz/linear-epidemid.
El modelo de epidemia que presentamos es una aplicación muy sencilla de álgebra lineal. En este blog hemos estado subiendo material de un curso de álgebra lineal que se imparte en la UNAM, y que ahora estamos impartiendo a distancia por la contingencia. A continuación ponemos el enlace a este curso y a otro material que te puede interesar.

Profesor Leonardo Martinez. Lo felicito por el estudio ofrecido. Le escribe Adolfo Valderrama Bielich. Nací en Lima, Perú, estudié Economía en la U de Lima y emigré a los EEUU en el 2002. Del 2016 al 2019 enseñe Matematicas en High School en Colorado, EEUU con licencia del estado de Colorado y ahora vendo paneles solares. He seguido de cerca las estadísticias de la pandemia con estas 3 páginas: https://ourworldindata.org/coronavirus?fbclid=IwAR0c_PRnaNYo9n5hK3E2Rqxf-DaJzLMd2xewmDNdrFWw12UUWtJpPFko5EI https://www.worldometers.info/coronavirus/country/us/ y http://covid19.healthdata.org/?fbclid=IwAR0SduMK5_R-XO6LP2JMtsbbR_1EjZXeBcd8pg7bU1FPQNhggjtWtTGZsz0. He trabajado con Desmos.com modelos de funciones bruja de agnes y Gaussianas. Por ejemplo para el total mundial de contagiados, he desarrollado estas funciones: https://www.desmos.com/calculator/zu3uh1ungu?fbclid=IwAR1A2ypmdnAx3DiSEkcqtBTv-tIgunPfLbcSGl8_Swo39WXhj25PgF3INJk que es consistente, pero como no conosco el ciclo porque depende es la suma de todos los paises y todavia no se sabe el de los EEUU, todavia no puedo predecir el total, pero si esta funcionando para Italia, España y Holanda. Como puedo hacer funciones de agnes y Gauss en Phyton? Atentos saludos Adolfo Valderrama Bielich.
Hola Adolfo. Gracias por la aportación de páginas. Aunque ojo, como enuncio en la entrada, mi objetivo nunca ha sido modelar al Covid.
No estoy muy seguro de en qué sentido se quieren usar funciones de Agnes o de Gauss para modelar la epidemia. Pero sí que se pueden hacer en Python. Recomendaría que le echaras un ojo a la documentación de NumPy, pues tiene mucha información de como usar diversas funciones.
Muchas gracias por el aporte Leonardo, lo anterior permite manejar mejor los escenarios y así poder entender que es lo mejor para todos.
Hola Álvaro. Gracias por leer y gracias por el comentario.
Excelente trabajo
Gracias por el comentario, Lindon.
Excelente aporte Leonardo. Muchas gracias por compartir estos datos.
Hola Christian. Gracias por el comentario.
Hola Christian. Gracias por tu comentario.
Si se incluyera probabilidad condicional para pasar de leve a grave y de grave a f, podría también utilizarse Markov?
La tercera ecuación en el Sistema de ecuaciones debe utilizer g(n) en lugar de l(n).
Muchas gracias por el ejempo
¿A qué te refieres en este caso con la probabilidad condicional? El modelo ya contempla cambios de leve a grave y de grave a fallecido.
Perfecto! mi duda era entonces si ya la estabas contemplando, no supe plantear la pregunta.
Encuentro que hay un pequeño error en la ecuación para g(n+1), pues entiendo que el último término en el lado derecho debe tener el factor g(n), no l(n).
Buen trabajo. Sencillo y elegante.
Hola Manuel. Gracias por la lectura y por la corrección. Ya debería reflejarse.
Buenas noches, cómo yo podría implementar este trabajo a excel?
Hola Jose. Es una buena pregunta. Podrías usar una columna para cada uno de los cinco estados , y en cada fila poner la fórmula que dependa de los estados de la fila anterior. Ya que tengas la cantidad de pasos que quieras, puedes hacer una gráfica en donde cada columna sea una función.
Gracias Leo, hay alguna forma en la que me puedas mostrar cómo realizar la gráfica en la herramienta de Excel?
Hola José. No tengo mucho tiempo para explicarlo. Pero como búsquedas, te puedo sugerir buscar en internet «cálculos recursivos en Excel», «recursiones en Excel» y «gráficas en Excel». Si no tienes tanta prisa, puedes escribirme a mi correo, y por ahí de junio que termine con los cursos que ando impartiendo, puedo apoyarte un poco más.
Se pueden hacer los markov en excel, y es bastante sencillo. Decision Modelling for Health Economic Evaluation de Andrew Briggs trae varios ejemplos de esto aplicados a Economía de la Salud. Dejo el link abajo.
(https://books.google.com.mx/books?id=x-URBAAAQBAJ&pg=PT52&lpg=PT52&dq=markov+models+briggs+excel&source=bl&ots=9qPrTbctNc&sig=ACfU3U3iX7B5p7wxWlynsyL2hjp-QDw0YA&hl=en&sa=X&ved=2ahUKEwjrsevgk9DpAhUCQq0KHTrVA-cQ6AEwEnoECAkQAQ#v=onepage&q=markov%20models%20briggs%20excel&f=false)
Profesor, tengo unas preguntas que me he formulado. Haber si me puedes contestar y muchas gracias.
(a) Piensa en la matriz de probabilidades de transición, en sus propiedades y sus implicaciones: ¿Hay conservación de la «masa» (se conserva la cantidad total de gente conforme el modelo evoluciona)?
(b) ¿Tendrá esta matriz un valor propio igual a 1? ¿Qué significa el vector propio asociado?
Hola Rey. De (a), sí, en efecto se conserva la cantidad total de gente conforme el modelo evoluciona. Esto lo puedes probar por inducción, y tiene que ver con que la suma de las entradas en cada columna es igual a 1. Sin embargo, ya que lo metes a una computadora es posible que haya algunos errores computacionales (por la forma en la que la compu hace las cuentas), que haga que haya algunos errores en las cifras decimales. De (b), es una muy buena pregunta. Justo por (a), si tomas v el vector de puros unos, se tiene que vA=v. En otras palabras, v es vector propio de A transpuesta, con valor propio 1. Esto quiere decir que 1 también es valor propio de A (los valores propios de una matriz son los mismos que los de su transpuesta). Ahora, v (el de puros unos), no necesariamente es eigenvector de A, pero sí debe haber uno que sí. Sería un vector v tal que Av=v. Esto se estudia en el tema de Cadenas de Markov en procesos estocásticos, y es un «estado estable», es decir, uno en el que ya no cambia el proceso representado por tu matriz. En esta entrada, un ejemplo de estos eigenvectores es el (0,0,0,1,0): si tienes una persona ya recuperada, entonces se queda recuperada. En fin, son algunas ideas. Si te interesa más, puedes echarle un ojo a temas de cadenas de Markov.
Una duda que disciplinas de las matemáticas contribuyen a modelar una epidemia?. Es para una tarea de la preparatoria. De antemano, muchas gracias por tu atención
Hola Braulio. Hay varias. Principalmente, son las ecuaciones diferenciales. Puedes echarle un ojo a esta página del modelo SIR: https://es.wikipedia.org/wiki/Modelo_SIR. Hay otras que también pueden ayudar, como el álgebra lineal y el cálculo. Saludos.