Introducción
En esta entrada estudiamos dos procedimientos generales que pueden ser útiles en la resolución de algunas construcciones geométricas.
Método analítico
Para problemas de construcciones geométricas en los cuales no es muy claro que pasos seguir, nos puede ayudar el método analítico el cual se divide en los siguientes pasos:
Análisis. Empezamos asumiendo que ya tenemos la figura que satisface las condiciones del problema y hacemos un dibujo aproximado de esta. A partir de esta figura indagamos que tipo de relación hay entre los datos que conocemos y los que no.
Construcción. Con la información obtenida llevamos a cabo nuestra construcción.
Demostración. Probamos que en efecto nuestra construcción nos lleva a la figura requerida.
Discusión. Hablamos sobre las condiciones bajo las cuales el problema puede ser resuelto, el número de soluciones posibles y otras observaciones.
A continuación, veremos un par de ejemplos.
($a$, $\angle A$, $b + c$)
Proposición 1. La mediatriz de un lado en todo triangulo siempre interseca al mayor de los lados restantes.
Demostración. Por contradicción, sea $\triangle ABC$ tal que $AC > AB$ y supongamos que la mediatriz de $BC$ interseca a $AB$ en $D$.
$\triangle DBC$ es isósceles, pues $D$ equidista a $B$ y a $C$,
$\Rightarrow \angle CBD = \angle DCB < \angle ACB$.
Por otro lado, sabemos que en todo triangulo al mayor de los lados siempre se opone el mayor de los ángulos, $\Rightarrow \angle CBD = \angle CBA > ACB$.
Lo cual es una contradicción, por tanto, $D \in AC$.
$\blacksquare$
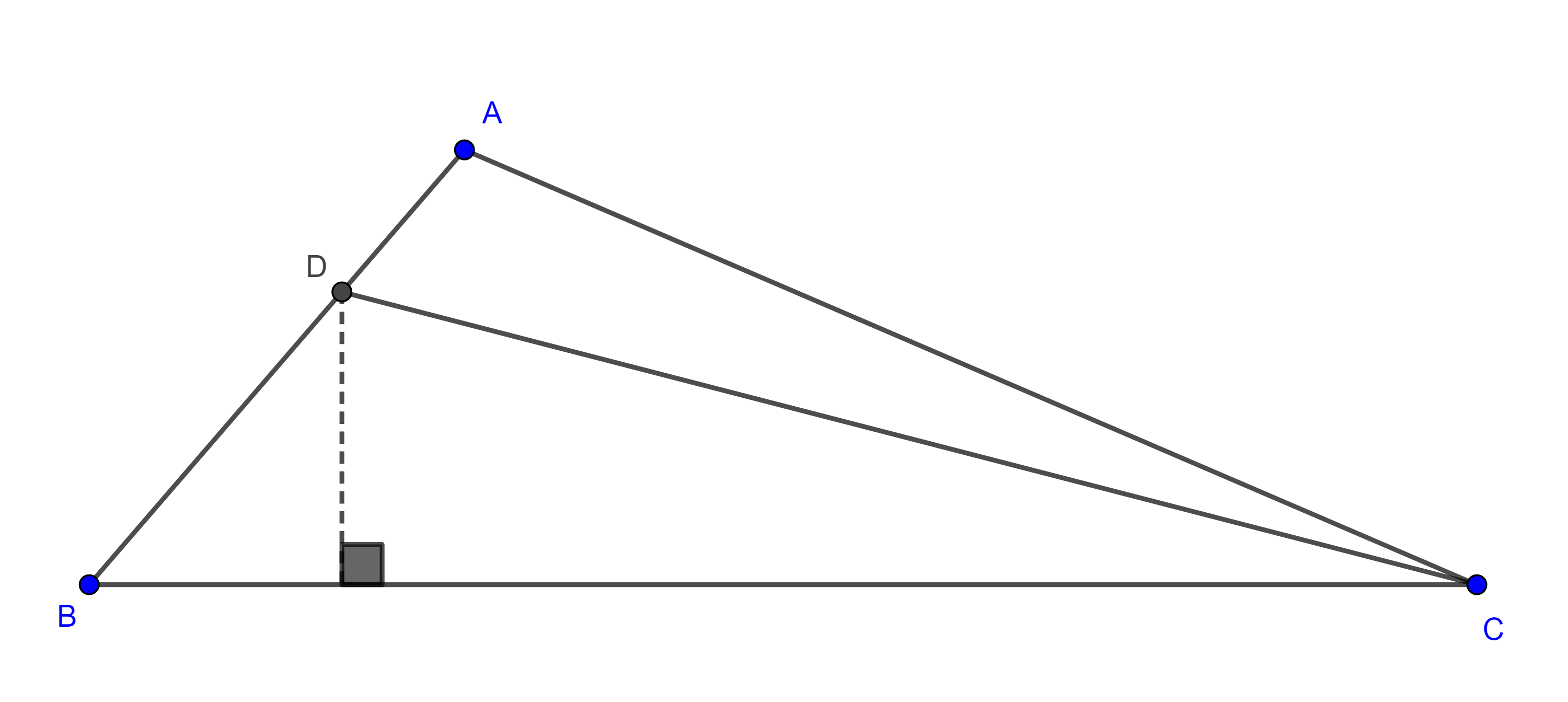
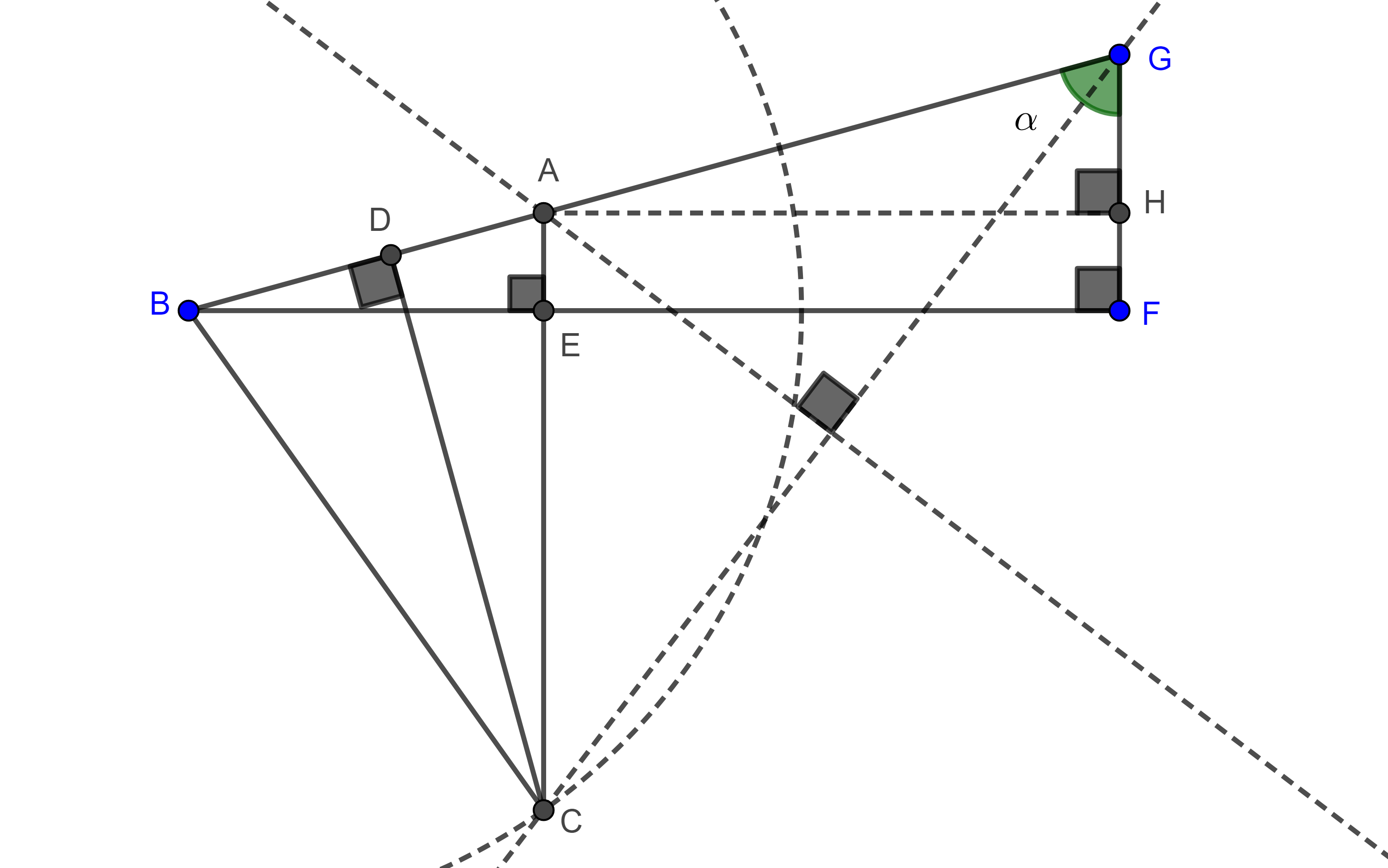
Problema 1. Construir un triángulo $\triangle ABC$ dados la base, el ángulo opuesto a la base y la suma de los lados restantes ($BC = a$, $\angle A = \alpha$, $AB + AC= c + b$).
Análisis. Supongamos que $\triangle ABC$ es el triángulo requerido, sea $D$ en la recta $AB$ tal que $AD = AC$. $\angle BAC$ es un ángulo exterior del triángulo isósceles $\triangle ACD$,
$\Rightarrow BAC = \angle D + \angle DCA = 2\angle D$
$\Rightarrow \angle D = \dfrac{\angle BAC}{2} = \dfrac{\alpha}{2}$.
Con estos elementos podemos construir el triángulo auxiliar $\triangle DBC$ y a partir de este a $\triangle ABC$.
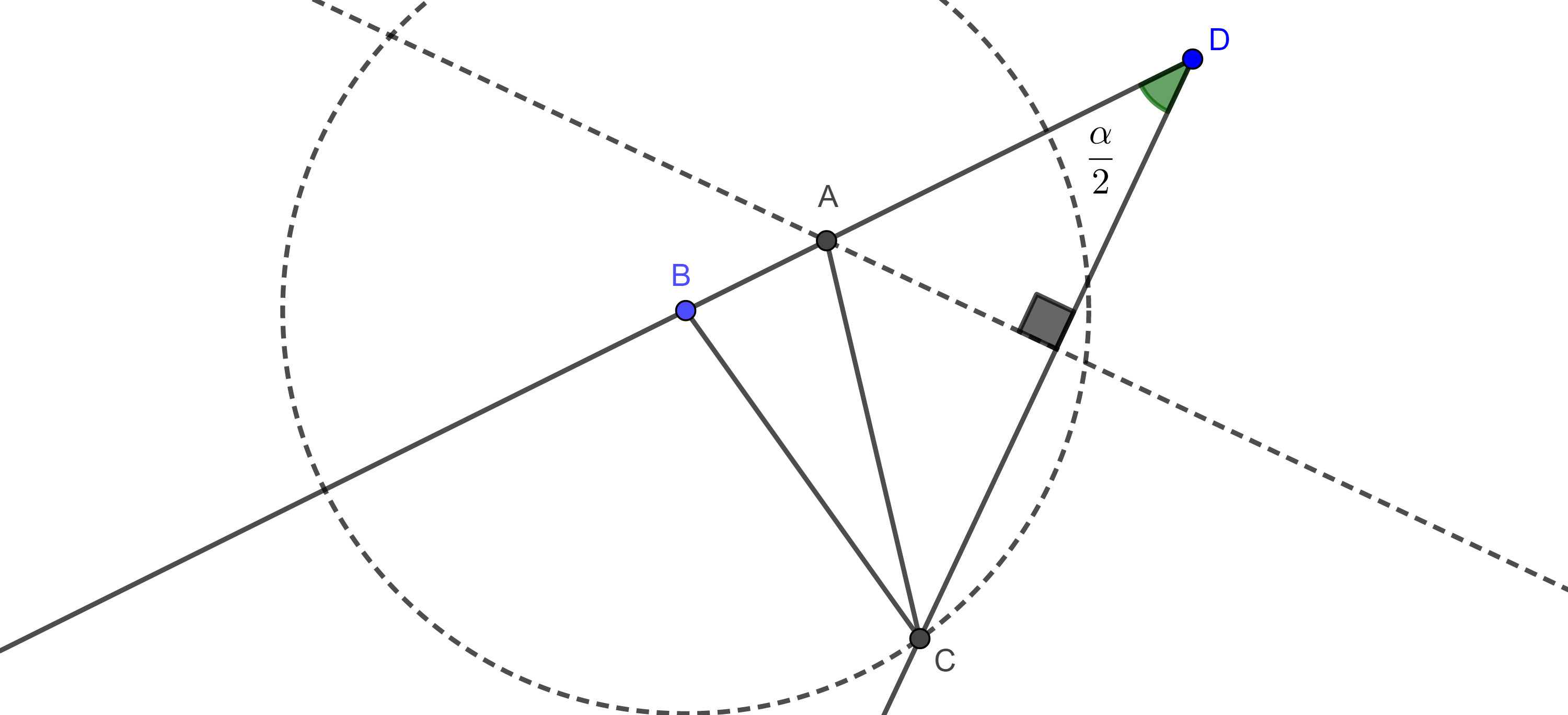
Construcción. Sobre un punto $D$ construimos el ángulo $\dfrac{\alpha}{2}$, sea $B$ sobre uno de los lados del ángulo tal que $DB = b + c$, dibujamos una circunferencia con centro en $B$ y radio $a$, $(B, a)$.
Sea $C$ la intersección de $(B, a)$ con el otro lado del ángulo $\dfrac{\alpha}{2}$.
Finalmente, el vértice $A$ de $\triangle ABC$, se encuentra en la intersección del lado $DB$, con la mediatriz de $CD$.
Demostración. Como $A$ es un punto en la mediatriz de $CD$, entonces $AD = AC$, y como $\triangle ADC$ es isósceles $\Rightarrow \angle DCA = \angle ADC = \dfrac{\alpha}{2}$.
Ya que $\angle BAC$ es ángulo exterior de $\triangle ADC$, es igual a la suma de los ángulos interiores no adyacentes a el $\Rightarrow \angle BAC = \angle DCA + \angle ADC = \alpha$.
Por otro lado, $BC = a$ y $AB + AC = AB + AD = b + c$, por construcción.
$\blacksquare$
Discusión. Por la proposición 2, notamos que es necesario que en el triángulo auxiliar $\triangle DBC$ se cumpla $DB > BC$, es decir $b + c > a$, para que la mediatriz de $CD$ interseque a $BD$.
También observamos que en la construcción de $\triangle DBC$, necesitamos que el radio de $(B, a)$ sea mayor o igual a la distancia de $B$ al segundo lado del ángulo $\alpha$, pues en caso contrario no es posible construir a $C$ y no habrá solución.
Finalmente, de cumplirse esta última condición puede haber una o dos soluciones distintas.
($a$, $\angle A$, $h_b + h_c$)
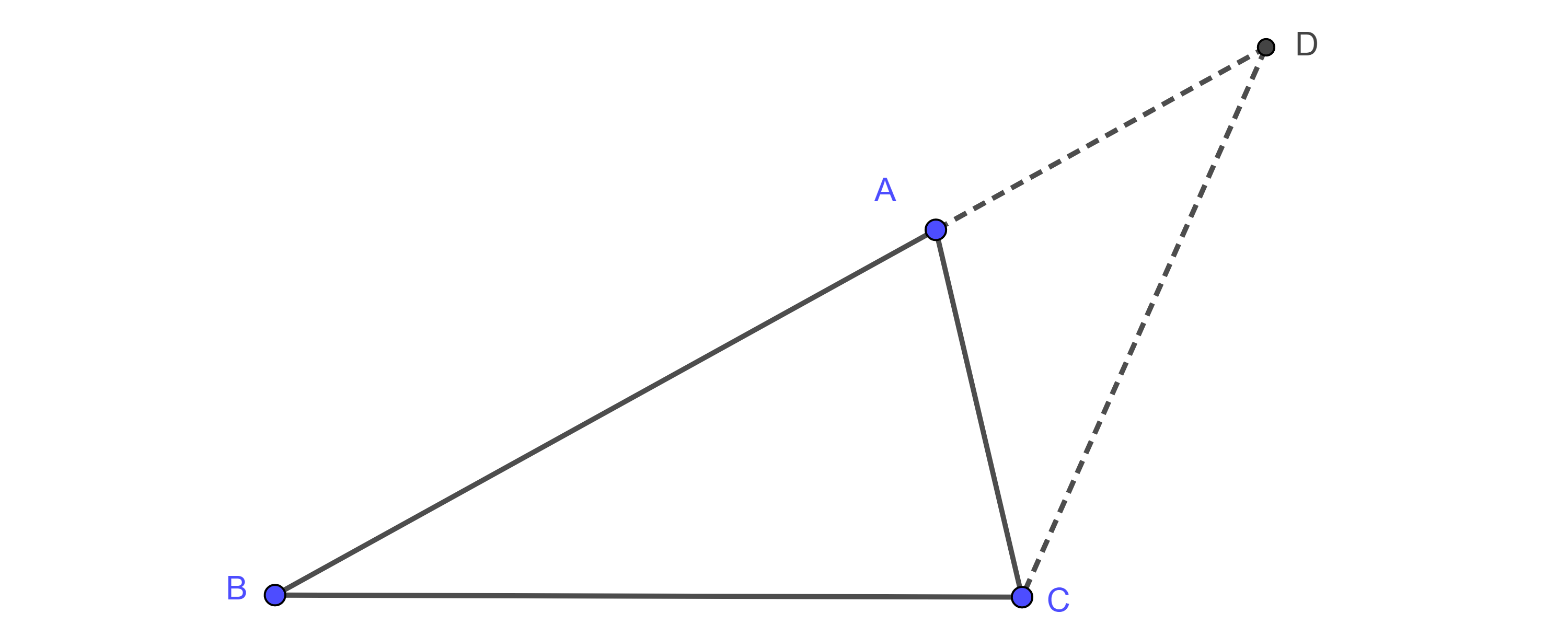
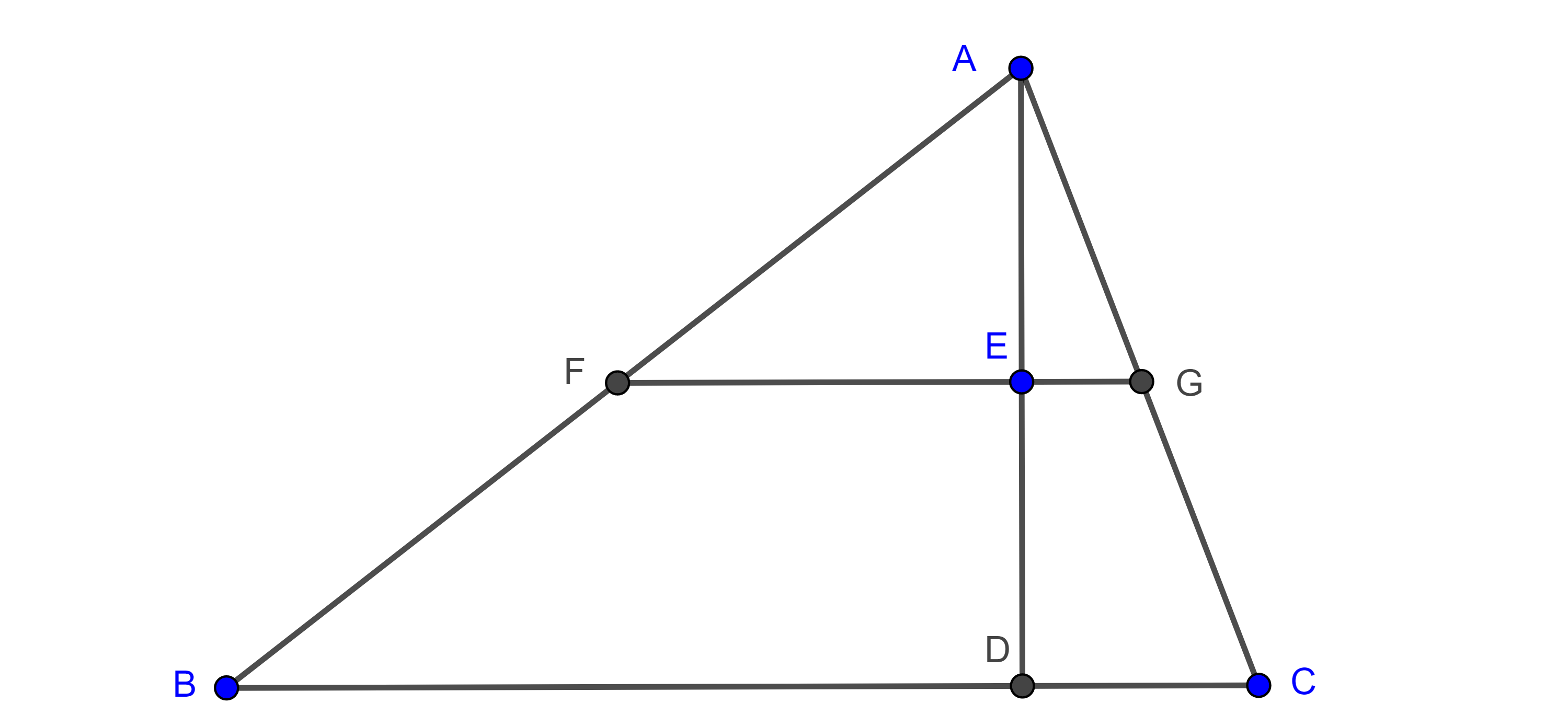
Problema 2. Construye un triángulo $\triangle ABC$ dados la base, el ángulo opuesto y la suma de las alturas perpendiculares a los otros dos lados ($BC = a$, $\angle A = \alpha$, $BD + CE = h_b + h_c$).
Análisis. Supongamos que $\triangle ABC$ es el triángulo requerido, y sean $BD = h_b$ y $CE = h_c$ las alturas por $B$ y $C$ respectivamente.
Sea $F$ sobre la recta $BD$ tal que $BF = BD + CE = h_b + h_c$.
Por $F$ trazamos una recta paralela a $AC$, la cual interseca a $AB$ en $G$, entonces $\angle BGF = \angle BAC = \alpha$ y $\angle GFB = \angle ADB = \dfrac{\pi}{2}$ por ser ángulos correspondientes.
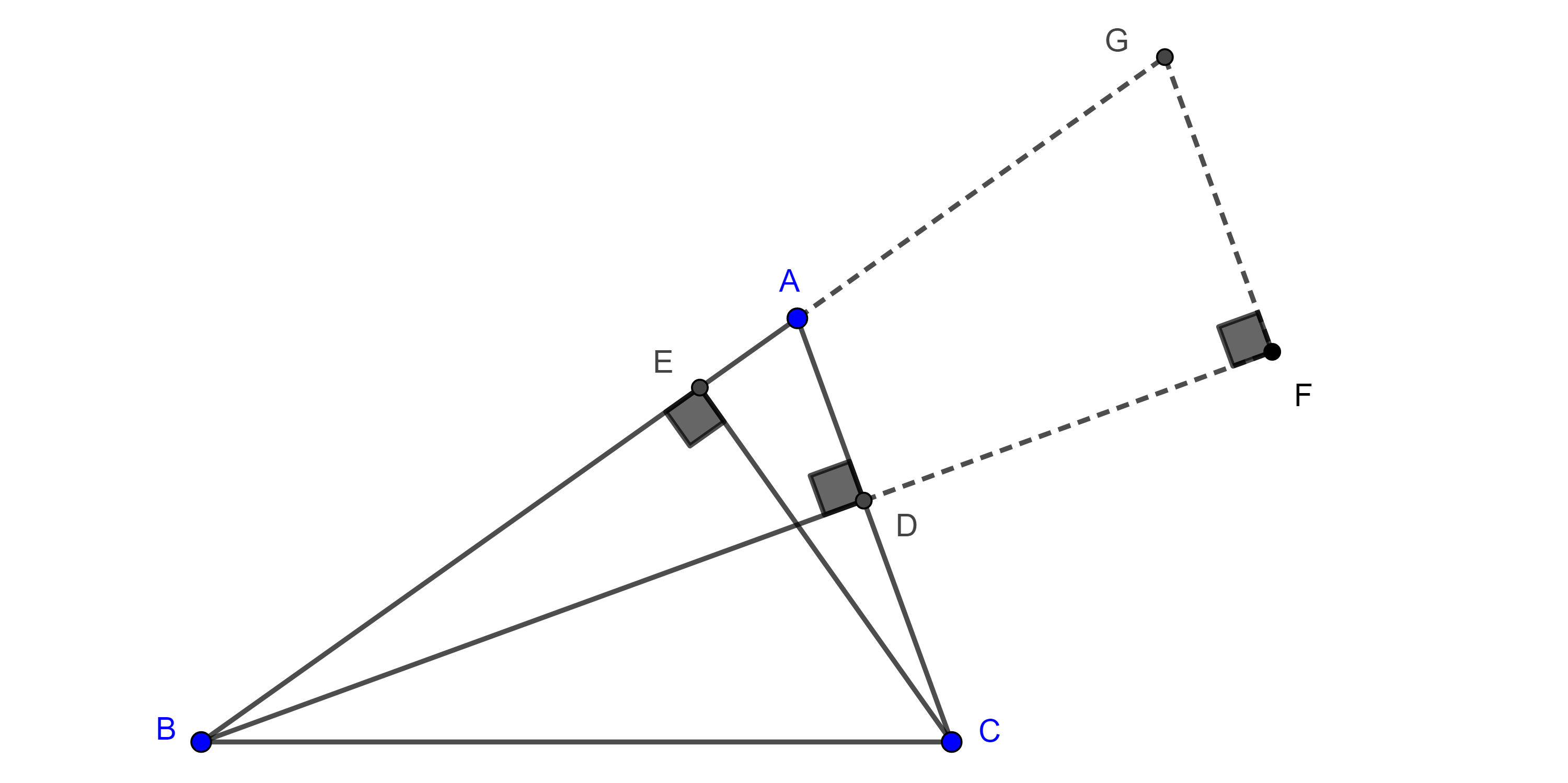
Construcción. De manera similar a la construcción del triángulo auxiliar $\triangle DBC$ del problema anterior, con la información que resulta del análisis ($BF = h_b + h_c$ y $\angle BGF = \alpha$), podemos construir el triángulo rectángulo auxiliar $\triangle BFG$.
Luego, trazamos una circunferencia con centro $B$ y radio $a$, $(B, a)$.
La intersección de $(B, a)$ con la bisectriz interior de $\angle BGF$ será el vértice $C$ y la intersección de $GB$ con la mediatriz de $GC$ será el vértice $A$.
Demostración. Por construcción $BC = a$, como $A$ está en la mediatriz de $GC$ entonces $\triangle AGC$ es isósceles por lo que $\angle GCA = \angle AGC$, pero $\angle AGC = \angle CGF$ pues $GC$ es bisectriz de $\angle AGF$,
$\Rightarrow \angle GCA = \angle CGF$ $\Rightarrow AC \parallel FG$
$\Rightarrow \angle BAC = \angle BGF = \alpha$
Como $AC \parallel FG$ entonces $BF \perp AC$.
Sean $BE$ y $CD$ las alturas de $\triangle ABC$ trazadas por $B$ y $C$ respectivamente.
Por $A$ trazamos una perpendicular a $AC$ que corta a $GF$ en $H$, como $\square AEFH$ es un rectángulo entonces $AH = EF$.
En los triángulos rectángulos $\triangle ADC$ y $\triangle GHA$ tenemos $AC = AG$ y $\angle DAC = \angle AGH$, por criterio de congruencia ALA $\triangle ADC \cong \triangle GHA$ $\Rightarrow CD = AH = EF$.
Por lo tanto, $BE + CD = BE + EF = BF = h_b + h_c$, por construcción.
$\blacksquare$
Discusión. Si el ángulo dado es obtuso entonces el triángulo rectángulo auxiliar $\triangle BFG$ incluirá al ángulo suplementario a $\angle A$ y el procedimiento será muy similar.
Notemos que $(B, a)$ puede intersecar a la bisectriz de $\angle BGF$ en cero, uno o dos puntos y por lo tanto existen cero, una o dos posibles soluciones.
Método de semejanza
Este método consiste en construir una figura semejante a la figura requerida omitiendo una de las condiciones dadas, la figura requerida se deriva a partir de la semejanza.
Ilustramos este método con un par de ejemplos.
($b$, $c$, $\dfrac{a}{h_a}$)
Problema 3. Construye un triangulo $\triangle ABC$ dados dos lados y la razón entre el tercer lado y la altura por el vértice opuesto ($AB = c$, $AC = b$, $\dfrac{BC}{AD} = \dfrac{a}{h_a}$).
Análisis. Supongamos que $\triangle ABC$ es el triángulo requerido, consideremos $D$, el pie de la altura desde $A$.
Sea $E \in AD$ tal que $AE = h_a$, por $E$ trazamos la paralela a $BC$ que interseca a $AB$ y a $AC$ en $F$ y $G$ respectivamente.
Como $\triangle ABC \sim \triangle AFG$, entonces
$\begin{equation} \dfrac{AF}{AG} = \dfrac{AB}{AC} = \dfrac{c}{b} \end{equation}$
y $\dfrac{FG}{AE} = \dfrac{BC}{AD} = \dfrac{a}{h_a}$,
como $AE = h_a \Rightarrow FG = a$
Construcción. Podemos construir el triángulo auxiliar $\triangle AFG$ con los siguientes datos, la base $FG = a$, la altura $AE = h_a$ y la razón entre los lados restantes $\dfrac{AF}{AG} = \dfrac{c}{b}$, este problema lo resolvimos en la entrada anterior.
Luego, sobre $AF$ construimos $B$ tal que $AB = c$ y sobre $AG$ construimos $C$ tal que $AC = b$.
Demostración. Por construcción se da la ecuación $(1)$, y por el reciproco del teorema de tales, esto implica $FG \parallel BC$ y $\triangle ABC \sim \triangle AFG$,
Sea $D = BC \cap AE$, el pie de la altura por $A$, entonces, $\dfrac{BC}{AD} = \dfrac{FG}{AE} = \dfrac{a}{h_a}$.
$\blacksquare$
Discusión. Debido a la construcción del triángulo auxiliar $\triangle AFG$ el problema tiene $0$, $1$ o $2$ soluciones posibles.
Construir un triángulo isósceles dado su incírculo
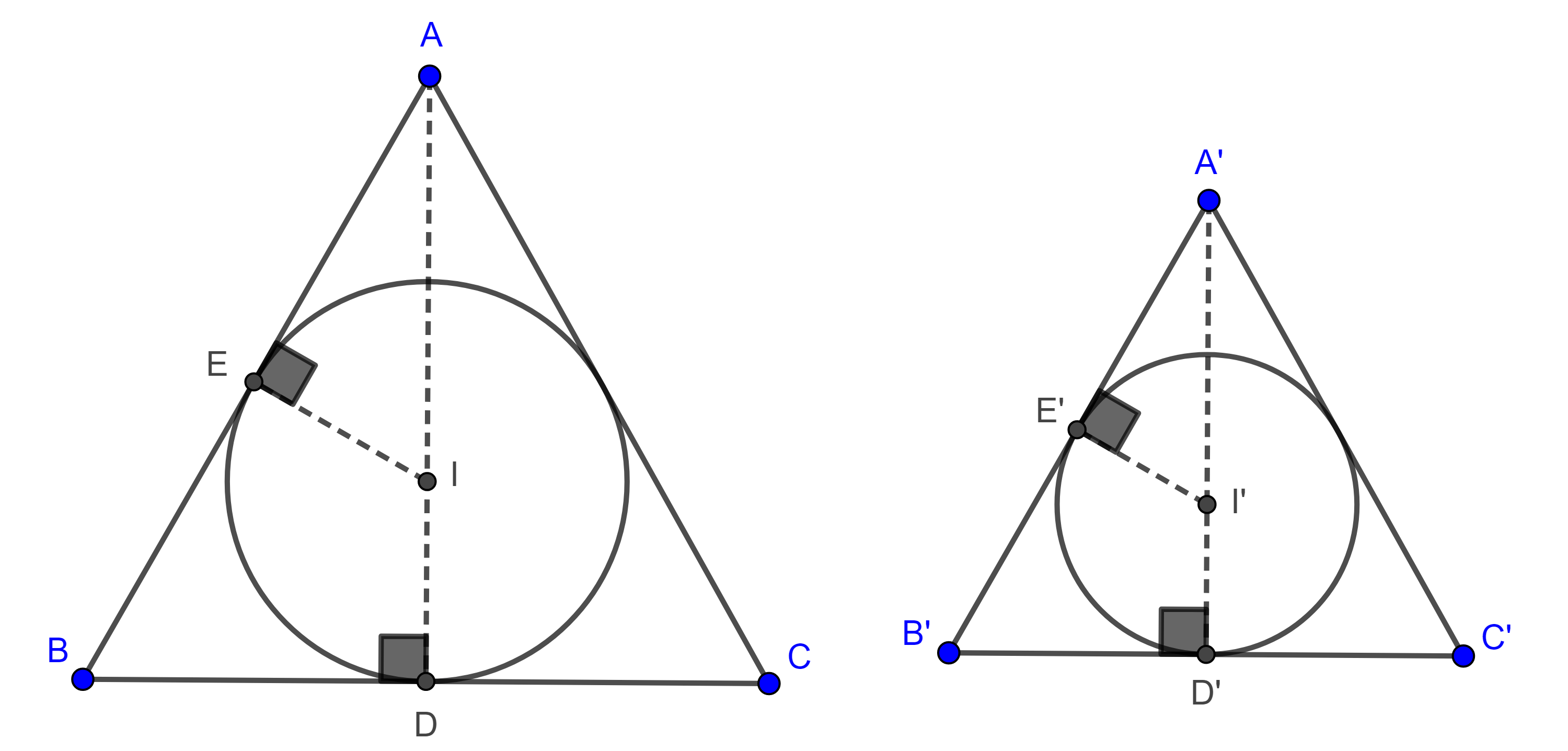
Proposición. 2 Dos triángulos isósceles son semejantes si la razón entre las alturas perpendiculares a las bases es igual a la razón entre sus inradios.
Demostración. Sean $\triangle ABC$ y $\triangle A’B’C’$ triángulos isósceles con $AB = AC$ y $A’B’ = A’C’$, $D$ y $D’$ los pies de las alturas desde $A$ y $A’$ respectivamente, consideremos $(I, r)$ y $(I’, r’)$ los incuncírculos de $\triangle ABC$ y $\triangle A’B’C’$ respectivamente.
Si $\dfrac{r}{r’} = \dfrac{AD}{A’D’} = \dfrac{h_a}{h_a’}$
$\Rightarrow h_a – r = \dfrac{rh_a’}{r’} – \dfrac{rr’}{r’} = \dfrac{r}{r’}(h_a’ – r’)$
$\Rightarrow \dfrac{AI}{A’I’} = \dfrac{h_a – r}{h’_a – r’} = \dfrac{r}{r’} = \dfrac{IE}{I’E’}$,
donde $E$ y $E’$ son los puntos de tangencia de $(I, r)$ y $(I’, r’)$ en $AB$ y $A’B’$ respectivamente.
Por criterio de semejanza hipotenusa-cateto, $\triangle AIE \sim \triangle A’I’E’$ $\Rightarrow$ $\angle EAI = \angle E’A’I’$, como $AI$ y $A’I’$ son bisectrices de $ \angle A$ y $ \angle A’$ respectivamente $\Rightarrow \angle A = \angle A’$.
Como $\angle B = \angle C$ y $\angle B’ = \angle C’$, obtenemos $2\angle B = 2\angle B’$, por cierto de semejanza AA, $\triangle ABC \sim \triangle A’B’C’$.
$\blacksquare$
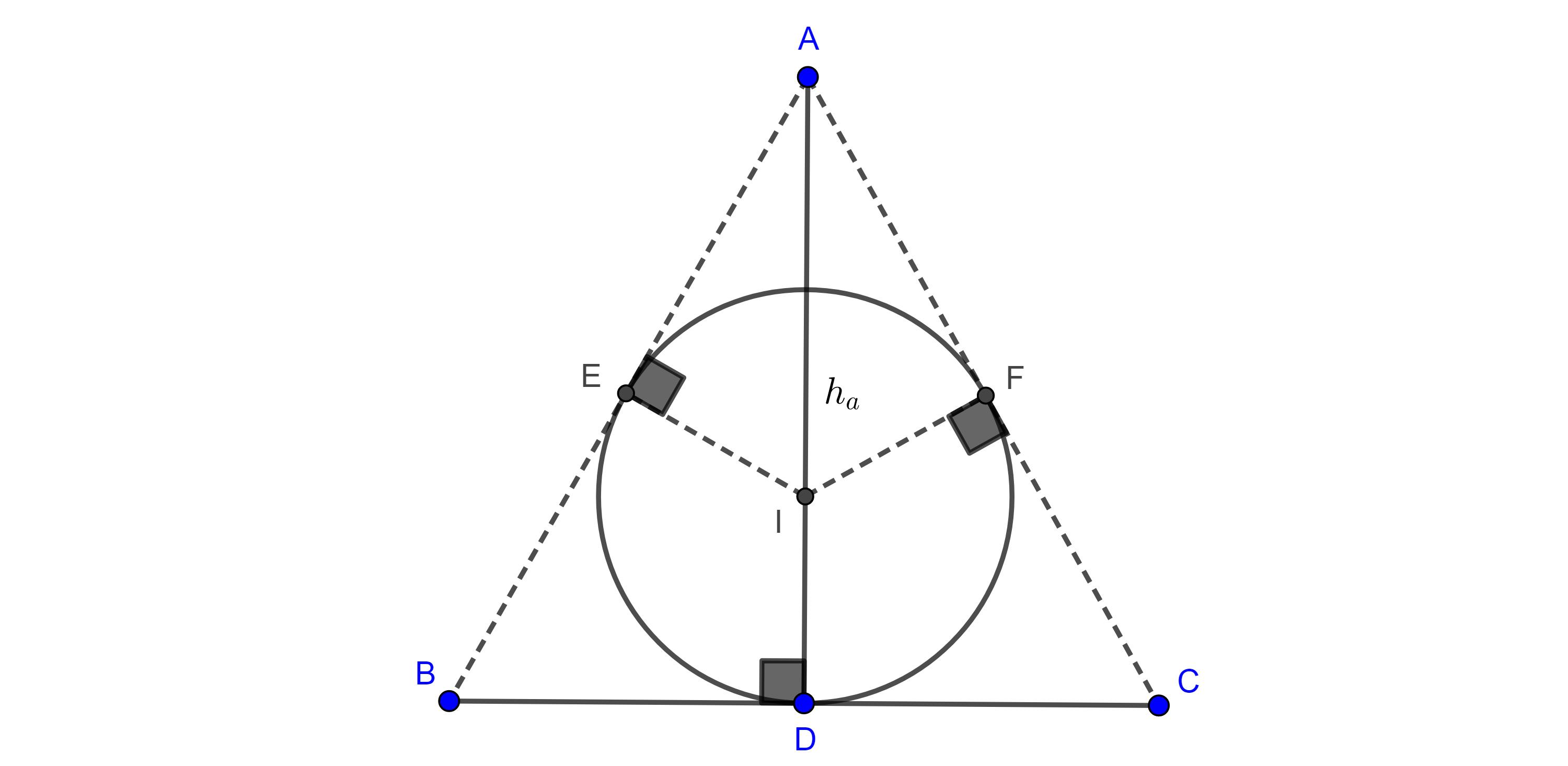
Problema 4. Dada una circunferencia $(I, r)$, construir un triángulo isósceles tal que $(I, r)$ es incírculo del triángulo y el cociente entre uno de los lados iguales del triángulo y la base es igual a una razón dada $\dfrac{p}{q}$.
Construcción. Construimos un triángulo $\triangle A’B’C’$ con $A’B’ = A’C’ = p$ y $B’C’ = q$, de este triangulo tomamos $h_a’$ la altura trazada desde $A’$ y $r’$ el inradio.
Ahora construimos $h_a = \dfrac{rh_a’}{r’}$.
Por un punto arbitrario $D \in (I, r)$ trazamos la tangente $l$ a $(I, r)$, en la recta $DI$, tomamos $A$ tal que $AD = h_a$, finalmente trazamos tangentes desde $A$ a $(I, r)$ y las intersecciones con $l$ serán los vértices $B$ y $C$.
Demostración. Sean $E$ y $F$ los puntos de tangencia de $AB$ y $AC$ respectivamente con $(I, r)$, por criterio de congruencia hipotenusa-cateto, $\triangle AIE \cong \triangle AIF$ por lo que $\angle BAI = \angle IAC$.
Como $AD \perp BC$, por criterio de congruencia ALA, $\triangle ADB \cong \triangle ADC$ $\Rightarrow AB = AC$, por lo tanto $\triangle ABC$ es un triángulo isósceles.
Dado que $\dfrac{h_a}{h_a’} = \dfrac{r}{r’}$, por la proposición 3, $\triangle ABC \sim \triangle A’B’C’$ y por tanto $\dfrac{AB}{BC} = \dfrac{A’B’}{B’C’} = \dfrac{p}{q}$.
$\blacksquare$
Más adelante…
La siguiente entrada tratara sobre homotecia, una transformación en el plano que agranda o achica una figura e incluso la invierte pero no cambia su forma, esta herramienta será muy útil en posteriores entradas.
Tarea moral
A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.
- Dados tres segmentos de longitudes $a$, $b$ y $c$ decimos que $x$ es la cuarta proporcional de $a$, $b$ y $c$ si $\dfrac{x}{a} = \dfrac{b}{c}$. Construir la cuarta proporcional de tres segmentos.
- Construye un triangulo dados la base, el ángulo opuesto a la base y la diferencia de los lados restantes ($a$, $\angle A$, $b – c$).
- Con los siguientes datos construye un triángulo, la base, el ángulo opuesto a la base y la diferencia de las alturas perpendiculares a los lados restantes ($a$, $\angle A$, $h_b – h_c$).
- Construye un cuadrado dada la suma de su lado $l$ y su diagonal $d$, $l + d$.
- Construye un triángulo dados un ángulo, la bisectriz del ángulo dado y la razón en que la bisectriz divide al lado opuesto.
Entradas relacionadas
- Ir a Geometría Moderna I.
- Entrada anterior del curso: Circunferencia de Apolonio.
- Siguiente entrada del curso: Homotecia.
- Otros cursos.
Fuentes
- Altshiller, N., College Geometry. New York: Dover, 2007, pp 17-37.
- Gomez, A. y Bulajich, R., Geometría. México: Instituto de Matemáticas, 2002, pp 45-50.
- Cut the Knot
Agradecimientos
Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»