Introducción

Probablemente recuerdes de los cursos de ecuaciones diferenciales algunos teoremas que, bajo ciertas condiciones, aseguran que existe una solución a una ecuación diferencial y además, esta es única. Puedes observar esta teoría a detalle en la página del curso Ecuaciones Diferenciales I en las secciones correspondientes a teorema de existencia y unicidad. Aquí probaremos el teorema como una aplicación del teorema de punto fijo de Banach. Comenzaremos resolviendo una ecuación diferencial particular.

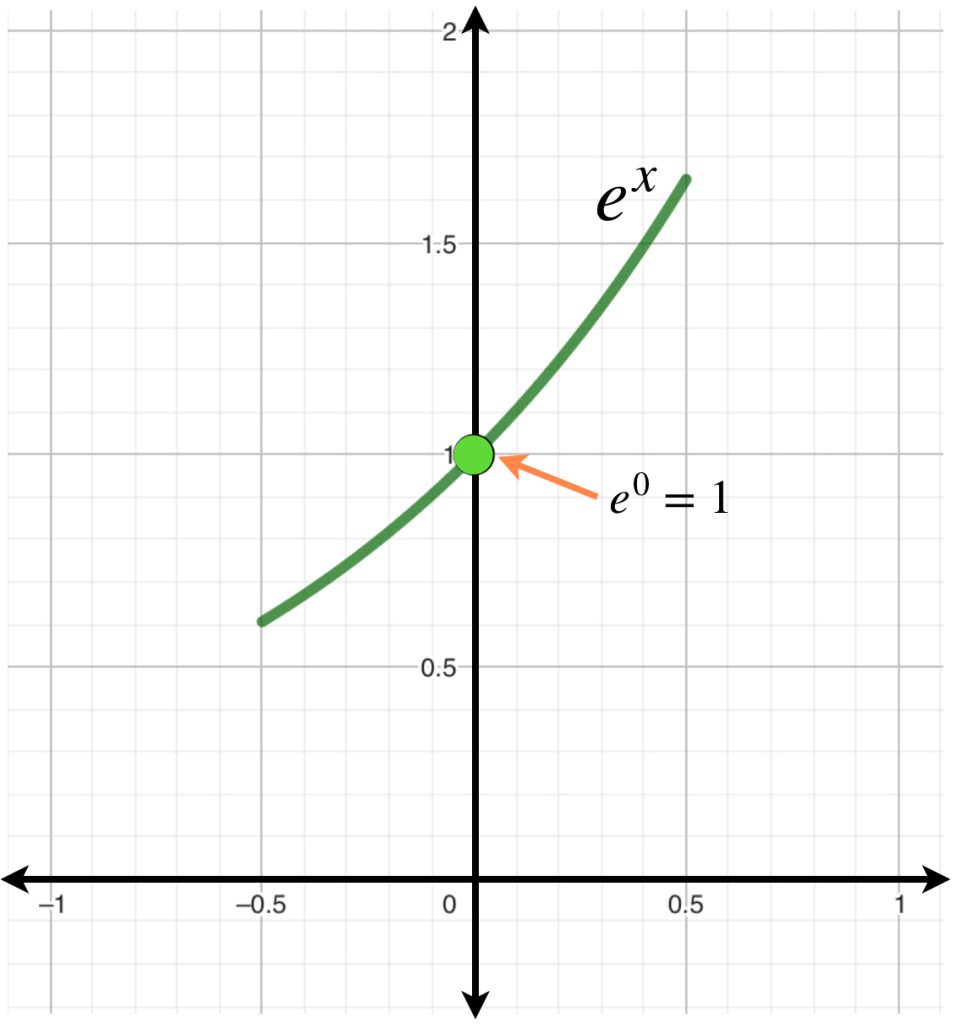
Ejemplo. $\dfrac{dy}{dx} = y,$ con condición inicial $y(0)=1.$

Considera la ecuación

$$\frac{d \, y(x)}{dx} = y(x), \, y(0)=1$$

Resolverla significa encontrar una función $y$ cuya derivada respecto a la variable $x$ coincida con ella misma. Ya que buscamos llegar a que la solución existe y es única, habría que pensar en hallarla dentro de un espacio métrico completo tras aplicar varias veces, una función contracción. En estas condiciones el teorema de punto fijo de Banach asegura que la sucesión generada converge a un punto fijo que, en este caso, representa la solución de la ecuación diferencial.

Comencemos identificando la contracción $\phi$ que servirá al objetivo. Si $f$ es punto fijo de $\phi$ se tiene que

$$\phi(f) = f$$

Y si además es solución de $\dfrac{dy}{dx} = y \,$ también cumple que

$$f'(x)=f(x)$$

Esto nos lleva a buscar a $f$ en el espacio de funciones continuas $\mathcal{C}[a,b]$ con la métrica uniforme $d_\infty$ y con $a,b \in \mathbb{R}$ tales que $0 \in [a,b],$ pues es donde se considera la condición inicial. Recordemos que en la entrada Convergencia uniforme y continuidad vimos propiedades que permiten concluir que este espacio sea completo. Así, el espacio identificado satisface las condiciones del teorema de punto fijo de Banach.

Supón que

\begin{align*}
&& f'(x) &=f(x)\\
&\Rightarrow &\int_{0}^{x} f'(t) \, dt & = \int_{0}^{x} f(t) \, dt \\
&\Rightarrow &f(x) \, – \, f(0) &= \int_{0}^{x} f(t) \, dt \\
&\Rightarrow &f(x) &= f(0) + \int_{0}^{x} f(t) \, dt
\end{align*}

De modo que definiremos $\phi$ como

$$\phi(f(x))\ := \, f(0) + \int_{0}^{x} f(t) \, dt $$

Si buscamos que la condición inicial sea $f(0) = 1,$ tenemos:

$$\phi(f(x))\ := \, 1 + \int_{0}^{x} f(t) \, dt$$

Existe un intervalo donde $\phi$ es contracción

A continuación probaremos que existe un intervalo $[a,b] \subset \mathbb{R}$ con $0 \in [a,b]$ donde la $\phi$ definida es contracción, es decir, que para cualquier $f,g \in \mathcal{C}[a,b]$ ocurre que $d_\infty(\phi(f)), \phi(g)) \leq \alpha \, d_\infty (f,g),$ para algún $\alpha \in (0,1).$

Proponemos $[a,b] = [-\frac{1}{2},\frac{1}{2}].$ Tenemos dos casos:

Si $0 \leq x.$

\begin{align*}
|\phi(f(x)) \, – \, \phi(g(x))|&= \left|1 + \int_{0}^{x} f(t) \, dt \, – \, \left(1 + \int_{0}^{x} g(t) \, dt \right)\right|\\
&= \left|\int_{0}^{x} f(t) – g(t) \, dt \right|\\
& \leq \int_{0}^{x} |f(t) – g(t)| \, dt\\
& \leq (x-0) d_\infty(f,g) \\
& \leq \frac{1}{2} d_\infty(f,g)
\end{align*}

Si $x < 0.$

\begin{align*}
|\phi(f(x)) \, – \, \phi(g(x))|&= \left|1 + \int_{0}^{x} f(t) \, dt \, – \, \left(1 + \int_{0}^{x} g(t) \, dt \right)\right|\\
&= \left|\int_{0}^{x} f(t) – g(t) \, dt \right|\\
&= \left|- \int_{x}^{0} f(t) – g(t) \, dt \right|\\
&= \left| \int_{x}^{0} f(t) – g(t) \, dt \right|\\
& \leq \int_{x}^{0} |f(t) – g(t)| \, dt\\
& \leq (0-x) d_\infty(f,g) \\
& \leq \frac{1}{2} d_\infty(f,g)
\end{align*}

De ambos casos se sigue que

\begin{align*}
d_\infty(\phi(f)), \phi(g)) &= \underset{x \, \in \, [-\frac{1}{2}, \frac{1}{2}]}{Sup} \, \{|\phi(f(x)) \, – \, \phi(g(x))|\} \\
&\leq \underset{x \, \in \, [-\frac{1}{2}, \frac{1}{2}]}{Sup} \, \left\{\frac{1}{2} d_\infty(f,g) \right\} \\
& = \frac{1}{2} d_\infty(f,g)
\end{align*}

Por lo tanto $d_\infty(\phi(f),\phi(g)) \leq \frac{1}{2} \, d_\infty(f,g)$

Lo cual prueba que $\phi$ es una contracción con constante $\alpha = \frac{1}{2}.$

Nota que $[-\frac{1}{2}, \frac{1}{2}]$ cumple que tiene al punto $0,$ valor considerado condición inicial y donde se busca que $f(0)=1.$ Por otro lado, el tamaño de este intervalo, o más específicamente, la distancia entre $0$ y $\frac{1}{2}$ permite concluir la última desigualdad. Aunque la solución que vamos a encontrar satisface la ecuación en todo $\mathbb{R},$ las condiciones de este método encuentran la solución en un intervalo pequeño.

Generamos la sucesión $(\phi^n)_{n \in \mathbb{N}}$

A continuación generaremos la sucesión a partir de iteraciones en la función constante que satisface que para todo $x \in [-\frac{1}{2}, \frac{1}{2}], \, f_0(x) := 1.$ El teorema de punto fijo de Banach nos dice que esto nos permite llegar en el límite a la función buscada.

$f_0(x) = 1$
$f_1(x) = \phi(f_0(x)) = 1 + \int_{0}^{x}1 \, dt = 1+x$
$f_2(x) = \phi(f_1(x)) = 1 + \int_{0}^{x}1+t \, dt = 1+x+ \frac{x^2}{2}$
$f_3(x) = \phi(f_2(x)) = 1 + \int_{0}^{x}1+t + \frac{t^2}{2}\, dt = 1+x+ \frac{x^2}{2}+ \frac{x^3}{6}$
.
.
.
Entonces $ \, \underset{n \to \infty}{lim} \,f_n(x) \, = \, \displaystyle \sum_{k=0}^{\infty}\dfrac{x^k}{k!} = e^x.$

Queda como ejercicio al lector confirmar que $\phi(e^x)= e^x$ es decir, que $e^x$ es punto fijo de $\phi$ y que satisface la ecuación diferencial.

Más adelante

Aplicaremos este método para resolver ecuaciones diferenciales más generales. Antes hablaremos de algunos resultados que usaremos en la prueba y veremos en la siguiente entrada.

Tarea moral

1. Evalúa $\phi(e^x)$ y confirma que es igual a $e^x.$
2. Propón otro intervalo $[a,b] \subset \mathbb{R}$ donde también funcione el método usado.
3. Resuelve la misma ecuación diferencial pero con condición inicial $y(1)=1.$

Enlaces

• Análisis Matemático.
• Enlace a entrada anterior.
• Enlace a entrada siguiente.

Introducción

En la entrada Contracciones mencionamos el teorema de punto fijo de Banach. Ahí mismo demostramos que si una contracción tiene un punto fijo, entonces este es único. En la entrada anterior vimos que la sucesión generada a partir de una contracción $\phi \,$ y un punto cualquiera $x_0$ del espacio métrico es de Cauchy. Estos dos resultados serán usados a continuación para expresar una demostración del teorema. Recordemos lo que expresa:

Teorema de punto fijo de Banach. Sea $(X,d)$ un espacio métrico completo y sea $\phi:X \to X$ una contracción, entonces:

1. Para cada $x_0 \in X$ la sucesión $(\phi^n(x_0))_{n \in \mathbb{N}} \,$ es de Cauchy y, en consecuencia $(\phi^n(x_0))_{n \in \mathbb{N}}$ converge a un punto $x^* \in X.$ $\, \, \phi^n$ representa la composición $\, \underset{n \, veces}{\underbrace{ \phi \circ … \circ \phi }}$
2. El punto $x^*$ descrito es punto fijo de $\phi.$
3. El punto fijo es único.
4. Podemos estimar la distancia de $\phi ^n(x_0)$ a $x^*$ usando la desigualdad:
   $$d( \phi ^n(x_0),x^*) \leq \frac{\alpha^n}{1-\alpha} \, d( x_0,\phi (x_0))$$

Demostración:
1. Se probó en la entrada anterior que la sucesión $(\phi^n(x_0))_{n \in \mathbb{N}} \,$ es de Cauchy. Como aquí agregamos el hecho de que el espacio es completo, concluimos que converge a algún punto $x^* \in X.$

2. Sea $x^* = \underset{n \to \infty}{lim}\, \phi ^n(x_0).$ Probemos que $x^*$ es punto fijo de $\phi.$
Sea $x_n= \phi^n(x_0).$ Apliquemos a cada término la función $\phi$ que como es contracción, entonces es Lipschitz y por tanto es continua, tal como se vio en la entrada Más conceptos de continuidad.

Como
$$(x_n)_{n \in \mathbb {N}} \to x^*$$
se sigue por lo visto en la entrada Funciones continuas en espacios métricos que
$$(\phi(x_n))_{n \in \mathbb {N}} \to \phi(x^*)$$
Pero para cada $n \in \mathbb{N}, \, \phi(x_n)= (x_{n+1})$ de modo que $(\phi(x_n))_{n \in \mathbb {N}}$ es una subsucesión de $(x_n)_{n \to \mathbb {N}} \to x^*.$ En consecuencia $(\phi(x_n))_{n \in \mathbb {N}}$ también converge a $x ^*.$
Pero por la unicidad del límite se sigue que.
$$ \phi(x^*) = x^*$$
Lo cual demuestra que $x^*$ es punto fijo de $\phi.$

3. Se probó en Contracciones.

4. En la demostración vista en la entrada anterior vimos que existe $N \in \mathbb{N}$ tal que si $n,m \geq N$ entonces

$$d(x_n,x_m) \leq \dfrac{\alpha^n}{1-\alpha} \, d( x_0,x_1)$$

Haciendo tender $m \to \infty$ se sigue que

$$d(x_n,x^*) \leq \dfrac{\alpha^n}{1-\alpha} \, d( x_0,x_1)$$

Por lo tanto

$$d(\phi^n(x_0),x^*) \leq \dfrac{\alpha^n}{1-\alpha} \, d( x_0,\phi(x_0)).$$

Que es lo que queríamos demostrar. Nota que esta última desigualdad nos permite acercarnos arbitrariamente al punto fijo de la contracción $\phi$ incluso sin conocerlo, pues su lado derecho puede elegirse tan pequeño como se desee, eligiendo un valor para $n$ suficientemente grande.

Ejemplo. $\phi : \mathbb{C} \to \mathbb{C}, \, \phi(z) = \dfrac{3iz}{4}$

Considera el espacio métrico completo $\mathbb{C}$ con la norma usual. Dejaremos como ejercicio probar que $\phi : \mathbb{C} \to \mathbb{C}, \, \phi(z) = \dfrac{3iz}{4}$ es contracción. La siguiente imagen muestra las primeras iteraciones de $\phi$ partiendo de $x_0 = 1.$ ¿A qué punto converge?

Si $n = 20,$ ¿puedes decir qué tan cerca está $\phi ^n(1)$ del punto fijo? Nota que puedes hacer una estimación sin tener que calcular la norma del punto $\phi ^n(1).$ Da el valor de $N \in \mathbb{N}$ a partir del cual la distancia al punto fijo sea menor que $\dfrac{1}{100}.$

Más adelante

Veremos el teorema de punto fijo de Banach aplicado en la demostración de la existencia y unicidad de la solución de una ecuación diferencial. Esto es, se buscan las funciones que satisfacen cierta ecuación. Estas funciones serán vistas como elementos de un espacio métrico completo. Como llegaremos a que la solución existe y es única, podemos esperar que dicha solución será punto fijo del espacio bajo cierta contracción.

Tarea moral

1. Resuelve las preguntas planteadas en el ejemplo arriba mencionado.
2. Considera el espacio de sucesiones acotadas en $\mathbb{R}$ con norma $\norm{(x_n)_{n \in \mathbb{N}}}= \underset{n \in \mathbb{N}}{sup}\, |x_n|.$
   a) Demuestra que la función $\phi(x_n)_{n \in \mathbb{N}}= (\frac{1}{2}(x_n))_{n \in \mathbb{N}}$ es contracción.
   b) Si $(x_0)$ es la sucesión acotada $(x_{0_n})_{n \in \mathbb{N}}.$ ¿Qué valores de $n \in \mathbb{N}$ satisfacen que la distancia entre $\phi^n(x_0)$ y la sucesión que es el punto fijo de $\phi$ sea menor que $\dfrac{1}{100}?$
3. Sea $X$ un espacio metrico y $\phi:X \to X$ una contracción. Demuestra que:
   a) Para cada $n \in \mathbb{N},$ la función $\phi^n$ es contracción.
   b) Si $x^*$ es punto fijo de $\phi,$ también lo es de $\phi^n.$
   c) Si $\psi: X \to X$ satisface que $\psi \circ \phi = \phi \circ \psi$ entonces $\psi$ tiene un punto fijo.
   d) Si $x^*$ es punto fijo para $\phi^k$ y para $\phi^{k+1}$ para algún $k \geq 2$ entonces $x^*$ es el punto fijo de $\phi.$

Enlaces

• Análisis Matemático.
• Enlace a entrada anterior.
• Enlace a entrada siguiente.

Introducción

En esta entrada continuaremos con la demostración del teorema de punto fijo de Banach, enunciado en la sección anterior. Vimos dos ejemplos de contracciones donde generamos una sucesión a partir de cualquier punto del espacio, evaluando la contracción recursivamente. En nuestros ejemplos observamos que la sucesión creada es convergente. ¿Lo será con cualquier contracción? Por lo pronto mostraremos que una sucesión así definida es de Cauchy.

Comencemos comprobándolo para el siguiente caso. Es más general que la primera función vista en Contracciones.

Ejemplo. $f(x)= \alpha x.$

En el espacio euclidiano $\mathbb{R}$ considera $f:\mathbb{R} \to \mathbb{R}$ definida como $f(x)= \alpha x,$ con $\alpha \in (0,1)$ constante. Entonces:
$$d(f(x),f(y))=d(\alpha \, x, \alpha \, y)=|\alpha \, x- \alpha \, y|= \alpha|x-y|=\alpha \, d(x,y)$$
Lo cual prueba que $f$ es contracción.

Veamos ahora que la sucesión generada al evaluar $f,$ partiendo de $x_0 \in \mathbb{R}$ es de Cauchy. Dado $x_0 \in \mathbb{R}$ tenemos:

$x_1:=f(x_0) = \alpha x_0$
$x_2:=f(x_1) = \alpha x_1 = \alpha^2 x_0$
$x_3:=f(x_2) = \alpha x_2 = \alpha^3 x_0$
.
.
.
$x_k:=f(x_{k-1}) = \alpha x_{k-1}= \alpha^k x_0$

Entonces la sucesión está dada por $(\alpha^n x_0)_{n \in \mathbb{N}}.$

A continuación, $ln(x)$ hace referencia al logaritmo natural de $x.$

Sea $\large{\varepsilon} >0$ y sea $N \in \mathbb{N}$ tal que $N > \dfrac{ln \left(\frac{\large{\varepsilon}}{|x_0|} \right)}{ln(\alpha)}.$

Como $\alpha \in (0,1), \, ln(\alpha)< 0.$ Se sigue que:

\begin{align*}
& &N \, ln(\alpha) &< ln \left(\frac{\varepsilon}{|x_0|} \right) \\
&\Rightarrow \, &exp \left(ln \left(\alpha^N \right) \right) &< exp \left( ln \left( \frac{\varepsilon}{|x_0|} \right) \right) \\
&\Rightarrow \, &\alpha^N&< \frac{\varepsilon}{|x_0|}
\end{align*}

La última desigualdad se usará en las siguientes líneas.

Sean $n,m \geq N.$ Supón sin pérdida de generalidad que $n \leq m$ entonces $\alpha^n \geq \alpha^m \geq 0 .$ Tenemos:

\begin{align*}
d(x_n,x_m) &= |x_n-x_m|\\
&=|\alpha^n x_0 \, – \, \alpha ^m x_0|\\
&= |\alpha ^n – \alpha^m||x_0|\\
&\leq \alpha ^n|x_0| \\
&\leq\alpha ^N |x_0| \\
&\leq \frac{\varepsilon}{|x_0|}|x_0| \\
&= \varepsilon
\end{align*}

Por lo tanto la sucesión $(\alpha^n x_0)_{n \in \mathbb{N}} \,$ es de Cauchy.

Pasemos a demostrar el caso general:

Proposición: Sea $(X,d)$ un espacio métrico, $\phi : X \to X$ una contracción con constante $\alpha \in (0,1)$ y sea $x_0 \in X.$ Entonces la sucesión $(\phi^n(x_0))_{n \in \mathbb{N}} \,$ es de Cauchy en $X.$

Demostración:
Comencemos con un análisis entre distancias de los primeros pares de puntos de la sucesión.

\begin{align*}
&d(x_1,x_2) = d(\phi(x_0),\phi(x_1)) &\leq \alpha d(x_0,x_1) \\
&d(x_2,x_3)=d(\phi(x_1),\phi(x_2)) \leq \alpha d(x_1,x_2) \leq \alpha (\alpha d(x_0,x_1)) &= \alpha^2 d(x_0,x_1)\\
&d(x_3,x_4) =d(\phi(x_2), \phi(x_3)) \leq \alpha d(x_2,x_3) \leq \alpha(\alpha^2d(x_0,x_1)) &= \alpha^3d(x_0,x_1)
\end{align*}

Por inducción sobre $n$ podemos concluir que la distancia entre cualquier punto de la sucesión y el siguiente está limitada por

\begin{equation}
d(x_n,x_{n+1})=d(x_n, \phi(x_n)) \leq \alpha^n d(x_0,x_1)
\end{equation}

Pasemos a probar que $(\phi^n(x_0))_{n \in \mathbb{N}} \,$ es de Cauchy en $X.$

Sea $\varepsilon>0$ y $N \in \mathbb{N}$ tal que $N \geq \, \dfrac{ln \left(\dfrac{\varepsilon(1- \alpha)}{d(x_0,x_1)}\right)}{ln (\alpha)}.$ Entonces si $n > N:$

\begin{align*}
& &n &> \dfrac{ln \left(\dfrac{\varepsilon(1- \alpha)}{d(x_0,x_1)}\right)}{ln (\alpha)} \\
&\Rightarrow & n \, ln (\alpha) &< ln \left(\dfrac{\varepsilon(1- \alpha)}{d(x_0,x_1)}\right) \\
&\Rightarrow & ln (\alpha^n) &< ln \left(\dfrac{\varepsilon(1- \alpha)}{d(x_0,x_1)}\right) \\
&\Rightarrow & exp(ln (\alpha^n)) &< exp \left(ln \left(\dfrac{\varepsilon(1- \alpha)}{d(x_0,x_1)}\right) \right) \\
&\Rightarrow & \alpha^n &< \dfrac{\varepsilon(1- \alpha)}{d(x_0,x_1)}
\end{align*}

\begin{equation}
\Rightarrow \, \dfrac{\alpha^n}{1- \alpha} d(x_0,x_1) < \large{\varepsilon}
\end{equation}

Sean $n,m \in \mathbb{N} \,$ tales que $n,m > N.$ Sin pérdida de generalidad supón que $m \geq n.$ Entonces $m \, = \, n+p$ para algún $p \in \mathbb{N}.$ A partir de la desigualdad del triángulo sabemos que la distancia entre el punto $x_n$ y el punto $x_m=x_{n+p}$ es menor igual que la suma de las distancias de todos los puntos de la sucesión que están entre ellos dos.

Se sigue:

\begin{align*}
d(x_n,x_m) &= d(x_n,x_{n+p})\\
&\leq d(x_n,x_{n+1}) +d(x_{n+1},x_{n+2}) …+ d(x_{n+p-2},x_{n+p-1})+d(x_{n+p-1},x_{n+p})\\
&\leq \alpha^n d(x_0,x_1) +\alpha^{n+1} d(x_0,x_1)+…+ \alpha^{n+p-2} d(x_0,x_1)+\alpha^{n+p-1} d(x_0,x_1) \text{ por ec. $(1)$}\\
&= (\alpha^n +\alpha^{n+1} +…+ \alpha^{n+p-2} +\alpha^{n+p-1} ) \, d(x_0,x_1) \\
&=\alpha^n \, (1+\alpha +…+\alpha^{p-2}+\alpha^{p-1}) \, d(x_0,x_1)
\end{align*}

Nota que $1+\alpha +…+\alpha^{p-2}+\alpha^{p-1}$ es la suma de los primeros términos de la serie $\sum_{k=0}^{\infty}\, \alpha^k.$ Probablemente has visto en otros cursos que ésta es una serie convergente y que $\sum_{k=0}^{\infty}\, \alpha^k \, = \dfrac{1}{1-\alpha}$, pues $|\alpha|<1$. Puedes consultarlo en la sección Cálculo Diferencial e Integral II: Series Geométricas. Entonces:

$$1+\alpha +…+\alpha^{p-2}+\alpha^{p-1} \leq \sum_{k=0}^{\infty}\, \alpha^k \, = \dfrac{1}{1-\alpha}$$

De modo que

\begin{align*}
\alpha^n \, (1+\alpha +…+\alpha^{p-2}+\alpha^{p-1}) \, d(x_0,x_1) &\leq \alpha^n \, \sum_{k=0}^{\infty}\, \alpha^k \, d(x_0,x_1) \\
&\leq \alpha^n \frac{1}{1- \alpha} \, d(x_0,x_1)\\
&< \varepsilon \text{ por ec. (2)}
\end{align*}

Por lo tanto $d(x_n,x_m) < \varepsilon \, $ lo cual demuestra que $(\phi^n(x_0))_{n \in \mathbb{N}} \,$ es una sucesión de Cauchy.

Más adelante

Terminaremos con la prueba del teorema de punto fijo de Banach. Mostraremos condiciones bajo las cuales esta sucesión de Cauchy es convergente y cómo aproximar la sucesión al punto de convergencia.

Tarea moral

1. Da un ejemplo de un espacio métrico completo y una función $\phi: X \to X$ que satisface que para cada $x,y \in X$ con $x \neq y, \, d(\phi(x), \phi(y)) < d(x,y)$ y que no tiene ningún punto fijo.
2. Prueba que si $X$ es un espacio métrico compacto y $\phi: X \to X$ satisface que para cada $x,y \in X$ con $x \neq y, \, d(\phi(x), \phi(y)) < d(x,y)$ entonces $\phi$ tiene un único punto fijo.

Enlaces

• Análisis Matemático.
• Enlace a entrada anterior.
• Enlace a entrada siguiente.

$\textcolor{Red}{\textbf{Extremos Restringidos (Multiplicadores de Lagrange)}}$

Supongase que se quieren hallar los valores extremos (máximo ó mínimo) de una función $f(x,y)$ sujeta a la restircción $x^2+y^2=1$; esto es, que $(x,y)$ está en el circulo unitario. Con mayor generalidad, podemos necesitar maximizar o minimizar $f(x,y)$ sujeta a la condición adicional de que $(x,y)$ también satisfaga una ecuación $g(x,y)=c$ donde $g$ es alguna función y $c$ es una constante. En el ejemplo $g(x,y)=x^2+y^2$ y $c=1$]. El conjunto de dichas $(x,y)$ es un conjunto de nivel de $g$.

En general, sean $f:u\subset \mathbb{R}^n\rightarrow \mathbb{R}$ y $g: u\subset \mathbb{R}^n\rightarrow \mathbb{R}$ funciones $C^1$ dadas, y sea $S$ el conjunto de nivel de $g$ con valor $c$. Recordar que el conjunto de nivel son los puntos $x\in
\mathbb{R}^n$ con $g(x)=c$] Cuando $f$ se restringe a $S$, de nuevo tenemos el concepto de máximos locales o mínimos locales de $f$ (extremos locales), y un máximo (valor mayor) o un minimo absoluto (valor menor) debe ser un extremo local.

$\textbf{Teorema.- Método de los multiplicadores de lagrange.}$ Sean $f:u\subset \mathbb{R}^n\rightarrow \mathbb{R}$ y $g: u\subset \mathbb{R}^n\rightarrow \mathbb{R}$ funciones $C^1$ con valores reales dados. Sean $x_0 \in u$ y $g(x_0)=c$, y sea $S$ el conjunto de nivel de $g$ con valor $c$. Suponer $\nabla g(x_0)\neq 0$.
Si $f|_s$ (f restringida a s) tiene un máximo o un mínimo local en $S$, en $x_0$, entonces existe un número real $\lambda$ tal que $\nabla f(x_0)=\lambda\nabla g(x_0)$.

$Demostrción$ Para $n=3$ el espacio tangente o plano tangente de $S$ en $x_0$ es el
espacio ortogonal a $\nabla g(x_0)$ y para $n$ arbitraria podemos dar la misma definición de espacio tangente de $S$ en $x_0$. Esta definición se puede motivar al considerar tangentes a trayectorias $c(t)$ que estan en $s$, como sigue: si $c(t)$ es una trayectoria en $S$ y $c(0)=x_0$, entonces $c'(0)$ es un vector tangente a $S$ en $x_0$, pero $$\frac{dg(c(t))}{dt}=\frac{d}{dt}(c)=0$$
Por otro lado usando regla de la cadena
$$\left.\frac{d}{dt}g(c(t))\right|_{t=0}=\nabla g(x_0)\cdot c'(0)$$
de manera que $\nabla g(x_0)\cdot c'(0)=0$, esto es, $c'(0)$ es ortogonal a $\nabla g(x_0)$.

Si $f|s$ tiene un máximo en $x_0$, entonces $f(c(t))$ tiene un máximo en $t=0$. Por cálculo de una variable, $\displaystyle\left.\frac{df(c(t))}{dt}\right|{t=0}=0$. Entonces por regla de la cadena $$0=\displaystyle\left.\frac{df(c(t))}{dt}\right|_{t=0}=\nabla f(x_0)\cdot c'(0)$$
Asi, $\nabla f(x_0)$ es perpendicular a la tangente de toda curva en $S$ y entonces tambien es perpendicular al espacio tangente completo de $S$ en $x_0$. Como el espacio perpendicular a este espacio tangente es una recta, $\nabla f(x_0)$ y $\nabla
g(x_0)$ son paralelos. Como $\nabla g(x_0)\neq 0$, se deduce que $\nabla f(x_0)$ es multiplo de $\nabla g(x_0)$.

$\textbf{Corolario.}$ Si $f$ al restringirse a una superficie $S$, tiene un máximo o un mínimo local en $x_0$, entonces $\nabla f(x_0)$ es perpendicular a $S$ en $x_0$.La geometria de los valores extremos restringidos.

$\textbf{Ejemplo.}$ Sea $S\subset\mathbb{R}^2$ la recta que pasa por $(-1,0)$ inclinada a $45^{o}$, y sea $f:\mathbb{R}^2 \rightarrow \mathbb{R}$ daa asi $f(x,y)=x^2+y^2$. Hallar los extremos de $f|_s$.

$Solución.$ Aqui $S=\left\{(x,y) | y-x-1=0 \right\}$ y por lo tanto hacemos $g(x,y)=-y-x-1$ y $c=0$. Tenemos $\nabla g(x,y)=-i+j \neq 0$. Los extremos relativos de $f|_s$ deben hallarse entre los puntos en que $\nabla f$ es ortogonal a $S$, esto es, inclinada a $-45^{o}$. Pero $\nabla f (x,y)=(2x.2y)$, que tiene la pendiente deseada sólo cuando $x=-y$, o cuando $(x,y)$ está sobre la recta L, que pasa por el origen inlinada a $-45^{o}$. Esto puede suceder en el conjunto $S$ sólo para el unico punto en
el que se intersecan L y S. Al referirnos a las curvas de nivel de $f$ se indica que este punto $(-\frac{1}{1},\frac{1}{2})$ es un mínimo relativo de $f|_s$ (Pero no de $f$).

$\textbf{Ejemplo.}$ Sea $f:\mathbb{R}^2\rightarrow \mathbb{R}$ dada asi $f(x,y)=x^2-y^2$ y sea $S$ el círculo de radio 1 alrededor del origen. Hallar los extremos de $f|_s$.

$Solución.$ El conjunto $S$ es la curva de nivel para $g$ con valor $t$. Donde $g:\mathbb{R}^2\rightarrow \mathbb{R}$, $(x,y) \rightarrow x^2+y^2$. La condición de que $\nabla f=\lambda \nabla g$ en $x_0$, es decir que $\nabla f$ y $\nabla g$ son pararlelos en $x_0$, es la misma que las curvas de nivel sean tangentes en $x_0$. Asi los puntos extremos de $f |_s$ son $(0,\pm 1)$ y $(\pm1,0)$. Evaluando $f$ hallamos que $(0,\pm 1)$ son mínimos y $(\pm1,0)$ son máximos. Usando Multiplicadores de
lagrange $\nabla f(x,y)=(2x,2y)$ y $\nabla g(x,y)=(2x,2y)$\ $\therefore$ \quad $(2x,-2y)=\lambda(2x,2y)$ cuya solución es $(0,\pm 1)$, $(\pm1,0)$.

$\textbf{Ejemplo.}$ Maximizar la función $f(x,y,z)=x+z$ sujeta a la restricción $x^2+y^2+z^2=1$

$Solución.$ Buscamos $\lambda$ y $(x,y,z)$ tales que $1=2x\lambda$, $0=2y\lambda$ y $1=2z\lambda$ $x^2+y^2+z^2=1$ la solución es $(\frac{1}{\sqrt{2}},0,\frac{1} {\sqrt{2}})$, $(-\frac{1}{\sqrt{2}},0,-\frac{1}{\sqrt{2}})$ comprobando los valores de $f$ en estos puntos podemos ver que el primer punto produce el máximo de $f$ y el segundo el mínimo.

$\textbf{Ejemplo.}$ Hallar los puntos extremos de $f(x,y,z)=x+y+z$ sujeto a las dos condiciones $x^2+y^2=2$ y $x+z=1$

$Solución.$ Aquí hay dos restricciones $g_1=(x,y,z)=x^2+y^2-2=0$ $g_2(x,y,z)=x+z-1=0$ asi, debemos encontrar $x,y,z,\lambda_1$ y $\lambda_2$ tales que $$\nabla f(x,y,z)=\lambda_1 \nabla g (x,y,z)+ \lambda_2 \nabla g_2(x,y,z)$$
$$g_1(x,y,z)=0 \quad y \quad g_2(x,y,z)=0$$
Calculando gradientes e igualando componentes, obtenemos

$\begin{eqnarray}
1=\lambda_1\cdot 2x+\lambda_2\cdot 1\\
1=\lambda_1 2y+\lambda_2\cdot 0\\
1=\lambda_1\cdot 0 + \lambda_2\cdot 1\\
x^2+y^2=2\\
x+z=1
\end{eqnarray}$

De (3) $\lambda_2=1$ y asi $2x\lambda_1=0$, $2y\lambda_1=1$.

Como la segunda implica $\lambda_1\neq 0$ $x=0$. Asi $y=\pm\sqrt{2}$ y $z=1$. Entonces los extremos deseados son $(0,\pm\sqrt{2},1)$.

Por inspección $(0,\sqrt{2},1)$ da un máximo relativo y $(0,-\sqrt{2},1)$ un mínimo relativo.

La condición $x+z=1$ implica que $z$ tambien está acotada. Se deduce que el conjunto de restricciones $S$ es cerrada y acotada,

Por lo tanto $f$ tiene un máximo y un mínimo en $S$ que se deben alcanzar en $(0,\sqrt{2},1)$ y $(0,-\sqrt{2},1)$ respectivamente.