Introducción

Para entender el método de los multiplicadores de Lagrange ilustraremos las ideas con un ejemplo.

Ejemplo. Sea $f:\mathbb{R}^{2}\rightarrow\mathbb{R}$ dada por
$$f(x,y)=(x+1)^{2}+y^{2}$$
En este caso vamos a encontrar los puntos críticos

$$\nabla f(x,y)=(2(x+1),2y)~\Rightarrow~\nabla f(x,y)=(0,0)~\Leftrightarrow~\begin{matrix}2(x+1)=0\\2y=0\end{matrix}~\Leftrightarrow~\begin{matrix}x=-1\\y=0\end{matrix}$$
por lo tanto el único punto crítico es $(-1,0)$ para ver si es máximo o mínimo nos fijamos que en la función
$$f(x,y)=(x+1)^{2}+y^{2}~\Rightarrow~f(x,y)\geq 0$$
en este caso cuando evaluamos en el punto crítico $(-1,0)$ se tiene
$$f(-1,0)=(-1+1)^{2}+0^{2}=0$$

por lo que podemos decir que el punto $(-1,0)$ es un punto mínimo.

La pregunta ahora es si la función alcanza un valor máximo, para ello debemos restringir el dominio de la función, en este caso al conjunto
$$\left\{(x,y)\in \mathbb{R}^{2}~|~|(x,y)|\leq 2\right\}$$

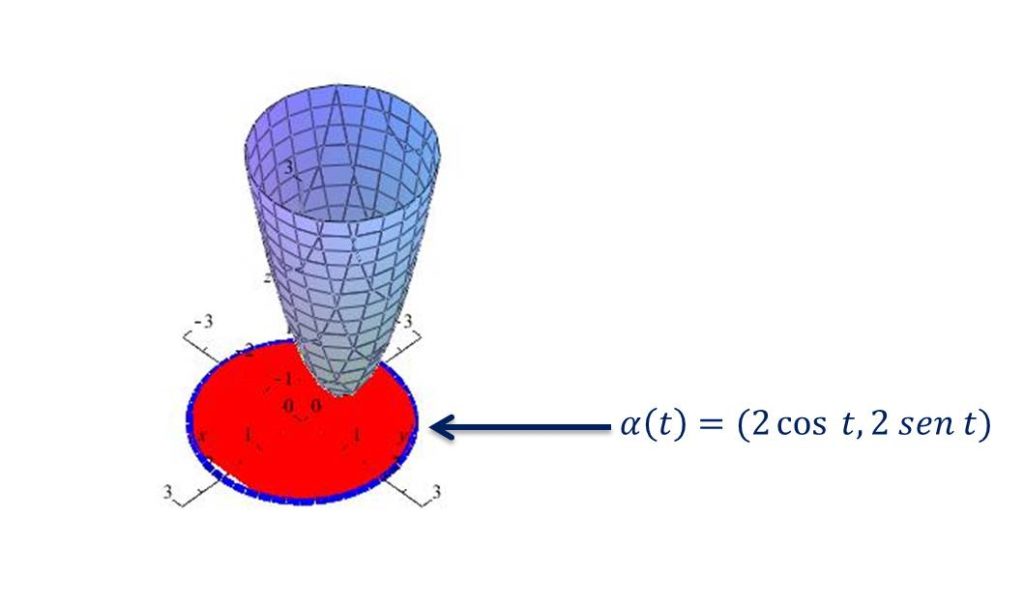
en la parte roja se calculo que $f$ alcanzaba un valor mínimo en $(-1,0)$ falta ver lo que ocurre en la frontera del conjunto, es decir en la parte azul. Esta parte se puede parametrizar.

donde $\alpha:[0,2\pi]\rightarrow\mathbb{R}^{2}$
Podemos entonces definir la función $g(t)=f\circ \alpha~(t)$ en este caso
$$g(t)=f\circ \alpha (t)=f(\alpha (t))$$
$$=f(2\cos~t,2 sen~t)$$
$$=(2\cos~t+1)^{2}+4 sen^{2}~t$$
$$=4\cos~t+5$$
lo que haremos ahora es encontrar los valores máximos y mínimos sobre g, en este caso

$$g'(t)=-4 sen t$$
por lo que
$$g'(t)=0~\Leftrightarrow~-4 sen t=0~\Leftrightarrow~t=0,~t=\pi,~t=2\pi$$
evaluando en g se tiene

$$g(0)=4\cos^{2}(0)+5$$
$$=9$$
$$g(\pi)=4\cos\pi+5$$
$$=1$$
$$g(2\pi)=4\cos^{2}(2\pi)+5$$
$$=9$$
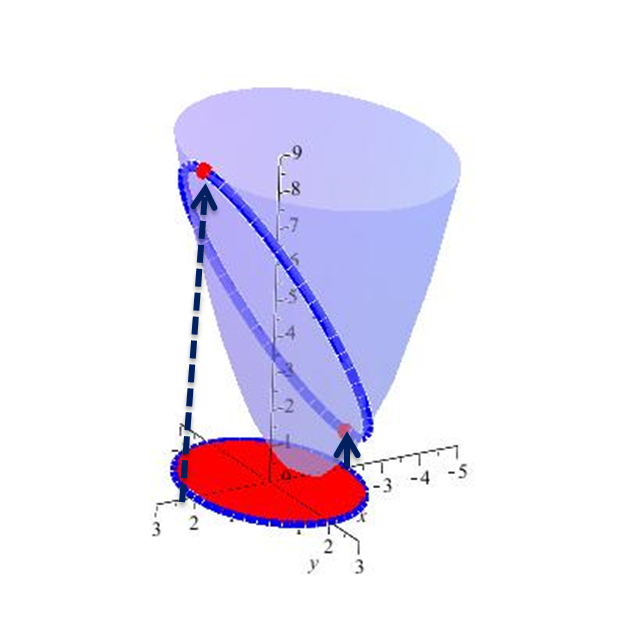
se tiene entonces que el máximo valor se alcanza en $t=0$, $t=2\pi$ y el mínimo valor se alcanza en $t=\pi$
Ahora sobre la frontera se tiene

$$\alpha(0)=(2\cos~0,2 sen~0)=(2,0)$$
$$\alpha(\pi)=(2\cos\pi, sen\pi)=(-2,0)$$
$$\alpha(2\pi)=(2\cos~2\pi, sen~2\pi)=(2,0)$$
por lo tanto tenenmos que el valor mínimo de f sobre el conjunto es 1 y que este valor se alcanza en $(-2,0)$

y su valor máximo sobre el conjunto es 9 y que este valor se alcanza en $(-2,0)$.\Por lo tanto comparando los valores de f en los puntos críticos que estan en el interior del conjunto
$$\left\{(x,y)\in\mathbb{R}^{2}~|~||(x,y)||=2\right\}$$
junto con los valores en la frontera de dicho conjunto, concluimos que f alcanza sus valores máximo y mínimo en los puntos $(-1,0)$ y $(2,0)$

El conjunto
$$\left\{(x,y)\in \mathbb{R}^{2}~|~||(x,y)||\leq 2\right\}$$
se puede considerarse como el conjunto de nivel de una función $g:\mathbb{R}^{2}\rightarrow\mathbb{R}$ en el caso de nuestro ejemplo la función g es
$$g(x,y)=x^{2}+y^{2}$$
Vamos a considerar los conjuntos de nivel de la función
$$f(x,y)=(x+1)^{2}+y^{2}$$
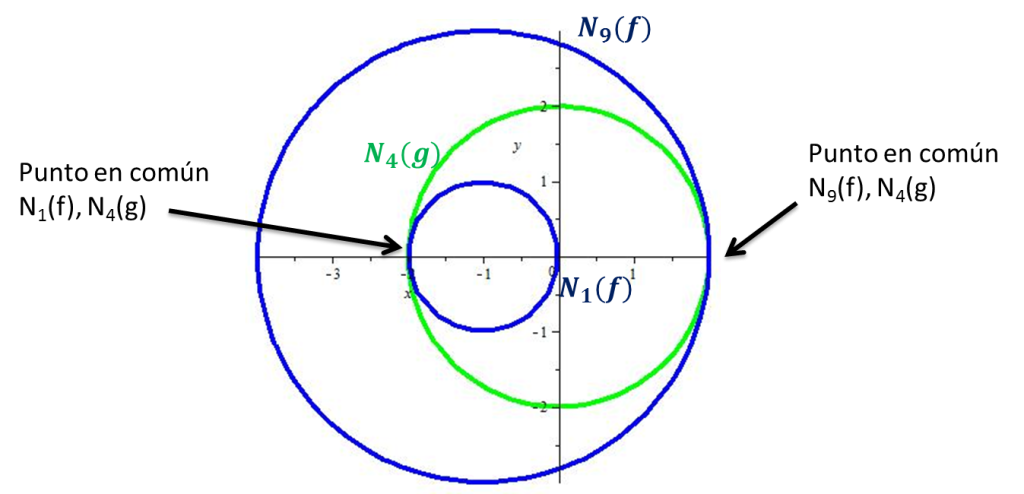
para $c=1$ y $c=9$ (que son los valores extremos que alcanzo f sobre el nivel 4 de g)

Observamos que estos conjuntos de nivel $N_{1}(f)$ y $N_{9}(f)$ se intersectan tangencialmente con $N_{4}(g)$ en los puntos $(-2,0)$ y $(2,0)$ que son justo los puntos en donde f alcanza sus valores extremos sobre la frontera del conjunto.Recordando que el gradiente de una función en un punto $x_{0}$ es ortogonal al conjunto de nivel que contiene a este punto, concluimos que los vectores
$$\nabla f(-2,0), \nabla g(-2,0)$$

deben de ser paralelos y lo mismo para

$$\nabla f(2,0),~\nabla g(2,0)$$
vamos averificar
$$\left(\begin{matrix}\nabla f(-2,0)=(-2,0)\\ \nabla g(-2,0)=(-4,0)\end{matrix}\right)~\Rightarrow~\nabla f(-2,0)=\frac{1}{2}\nabla g(-2,0)$$
$$\left(\begin{matrix}\nabla f(2,0)=(6,0)\\ \nabla g(2,0)=(4,0)\end{matrix}\right)~\Rightarrow~\nabla f(2,0)=\frac{3}{2}\nabla g(2,0)$$

Conjeturamos lo siguiente:
Si tenemos una función $f$ para la cual queremos calcular sus valores extremos sobre un conjunto de nivel de una función $g$ y localizar los puntos de este conjunto en los cuales alcanza estos valores extremos, es suficiente con encontrar los puntos $\hat{x}\in N_{c}(g)$ en los cuales se satisface que

$$\nabla f(\hat{x})=\lambda\nabla g(\hat{x})$$

Teorema 1. Método de los multiplicadores de lagrange.

Sean $f:u\subset \mathbb{R}^n\rightarrow \mathbb{R}$ y $g: u\subset \mathbb{R}^n\rightarrow \mathbb{R}$ funciones $C^1$ con valores reales dados. Sean $x_0 \in u$ y $g(x_0)=c$, y sea $S$ el conjunto de nivel de $g$ con valor $c$. Suponer $\nabla g(x_0)\neq 0$. Si $f|_s$ (f restringida a s) tiene un máximo o un mínimo local en $S$, en $x_0$, entonces existe un número real $\lambda$ tal que $\nabla f(x_0)=\lambda\nabla g(x_0)$.

Demostración. Para $n=3$ el espacio tangente o plano tangente de $S$ en $x_0$ es el
espacio ortogonal a $\nabla g(x_0)$ y para $n$ arbitraria podemos dar la misma definición de espacio tangente de $S$ en $x_0$. Esta definición se puede motivar al considerar tangentes a trayectorias $c(t)$ que estan en $s$, como sigue: si $c(t)$ es una trayectoria en $S$ y $c(0)=x_0$, entonces $c'(0)$ es un vector tangente a $S$ en $x_0$, pero
$$\frac{dg(c(t))}{dt}=\frac{d}{dt}(c)=0$$
Por otro lado usando regla de la cadena
$$\left.\frac{d}{dt}g(c(t))\right|{t=0}=\nabla g(x_0)\cdot c'(0)$$

de manera que $\nabla g(x_0)\cdot c'(0)=0$, esto es, $c'(0)$ es ortogonal a $\nabla g(x_0)$. Si $f|_s$ tiene un máximo en $x_0$, entonces $f(c(t))$ tiene un máximo en $t=0$. Por cálculo de una variable, $\displaystyle\left.\frac{df(c(t))}{dt}\right|{t=0}=0$. Entonces por regla de la cadena

$$0=\displaystyle\left.\frac{df(c(t))}{dt}\right|_{t=0}=\nabla f(x_0)\cdot c'(0)$$
Asi, $\nabla f(x_0)$ es perpendicular a la tangente de toda curva en $S$ y entonces tambien es perpendicular al espacio tangente completo de $S$ en $x_0$. Como el espacio perpendicular a este espacio tangente es una recta, $\nabla f(x_0)$ y $\nabla g(x_0)$ son paralelos. Como $\nabla g(x_0)\neq 0$, se deduce que $\nabla f(x_0)$ es multiplo de $\nabla g(x_0)$. $\square$

Ejemplo. Use el método de los multiplicadores de Lagrange para encontrar los valores extremos de la función $f:\mathbb{R}^{2}\rightarrow\mathbb{R}$ dada por
$$f(x,y)=2x+3y$$ sobre la restricción
$$x^{2}+y^{2}=4$$

Solución. En este caso la restricción la vemos como el conjunto de nivel cero de la función
$$g(x,y)=x^{2}+y^{2}-4$$
y tenemos entonces que
$$\left(\begin{matrix}\nabla f=(2,3)\\ \nabla g=(2x,2y)\end{matrix}\right)~\Rightarrow~(2,3)=\lambda (2x,2y)$$
tenemos el sistema

$$\left(\begin{matrix}2=2 \lambda x\\ 3= \lambda 2y \end{matrix}\right)~\Rightarrow~\left(\begin{matrix}\lambda=\frac{1}{x}\\ \lambda =\frac{3}{2}y \end{matrix}\right)~\Rightarrow~\frac{1}{x}=\frac{3}{2}y~\Rightarrow~y=\frac{3}{2}x$$
dicho valor se sustituye en la restricción

$$x^{2}+\left(\frac{3}{2}x\right)^{2}=4~\Rightarrow~x^{2}+\frac{9}{4}x^{2}=4~\Rightarrow~\frac{13}{4}x^{2}=4~\Rightarrow~13x^{2}=16~\Rightarrow~x^{2}=\frac{16}{13}~\Rightarrow~|x|=\frac{4}{\sqrt{13}}$$
por lo que
$$\left(\begin{matrix}y=\frac{3}{2}(\frac{4}{\sqrt{13}})=\frac{6}{\sqrt{13}}\\y=-\frac{3}{2}(\frac{4}{\sqrt{13}})=-\frac{6}{\sqrt{13}} \end{matrix}\right)$$
evaluando en nuestra función

El método de Lagrange se puede utilizar cuando hay más de una ecuación de restricción, pero se debe añadir otro multiplicador por cada restricción adicional. Si se requiere hallar los valores extremos de $f(x,y,z)$ sujetos a las restricciones $g(x,y,z)=0$ y $h(x,y,z)=0$ entonces la condición de Lagrange es
$$\nabla f=\lambda\nabla g+\mu \nabla h$$
sujeto a
$$g(x,y,z)=0$$
$$h(x,y,z)=0$$

Ejemplo. La intersección del plano
$$x+\frac{1}{2}y+\frac{1}{3}z=0$$
con la esfera
$$x^{2}+y^{2}+z^{2}=1$$ es un circulo. Halle el punto sobre este círculo con coordenada $x$ máxima
$\small{Solución}$ Se requiere maximizar la función
$$f(x,y,z)=x$$
sujeta a
$$x+\frac{1}{2}y+\frac{1}{3}z=0,~~~x^{2}+y^{2}+z^{2}=1$$
tenemos entonces
$$\left(\begin{matrix}\nabla f=(1,0,0)\\ \nabla g=\left(1,\frac{1}{2},\frac{1}{3} \right)\\ \nabla h=\left(2x,2y,2z \right) \end{matrix}\right)~\Rightarrow~(1,0,0)=\lambda \left(1,\frac{1}{2},\frac{1}{3} \right)+\mu (2x,2y,2z)$$

es decir
$$\begin{matrix}\lambda+\mu 2x=1\\ \frac{1}{2}\lambda+\mu 2y=0\\ \frac{1}{3}\lambda+\mu 2z=0 \end{matrix}~\Rightarrow~\begin{matrix}\mu=\frac{1-\lambda}{2x}\\ \lambda=-4\mu y\\ \lambda=-6\mu z\end{matrix}$$
las dos últimas nos llevan a
$$-4\mu y=-6\mu z~\Rightarrow~y=\frac{3}{2}z$$
este valor se sustituye en la primer restricción (plano)
$$x+\frac{1}{2}\left(\frac{3}{2}z\right)+\frac{1}{3}z=0~\Rightarrow~x=-\frac{13}{12}z$$
ambos valores se sustituyen en la segunda restricción (esfera)

$$\left(-\frac{13}{12}z\right)^{2}+\left(\frac{3}{2}z\right)^{2}+z^{2}=1~\Rightarrow~z=\pm\frac{12}{7\sqrt{13}}$$
por lo que los valores de $x,y$ son
$$x=\pm\frac{\sqrt{13}}{7}$$
$$y=\pm\frac{18}{7\sqrt{13}}$$
Tenemos entonces los puntos
$$P=\left(-\frac{\sqrt{13}}{7},\frac{18}{7\sqrt{13}},\frac{12}{7\sqrt{13}}\right),~~Q=\left(\frac{\sqrt{13}}{7},-\frac{18}{7\sqrt{13}},-\frac{12}{7\sqrt{13}}\right)$$
donde $Q$ es el punto con mayor coordenada $x$.