Introducción
En este apartado se abordará el tema de tasas equivalentes, el cual nos proporciona de una herramienta bastante útil, ya que nos permites poder obtener cualquier combinación posible de una tasas de interés efectiva a una nominal o a una instantánea. En pocas palabras, cualquier combinación posible
Definición de Tasa Equivalente
Una tasa equivalente es aquella que genera la misma cantidad de dinero, en el mismo tiempo, dicho con otras palabras, producen el mismo efecto de acumulación, después de un tiempo determinado, sin importar la periodicidad de pago, es decir, no importa que la periodicidad de pago no sea la misma.
Reglas de aplicación
Para poder aplicar éste concepto se hará sus de la triple igualdad, y en la siguiente imagen se muestra una descripción de todas las combinaciones posibles que se pueden realizar:
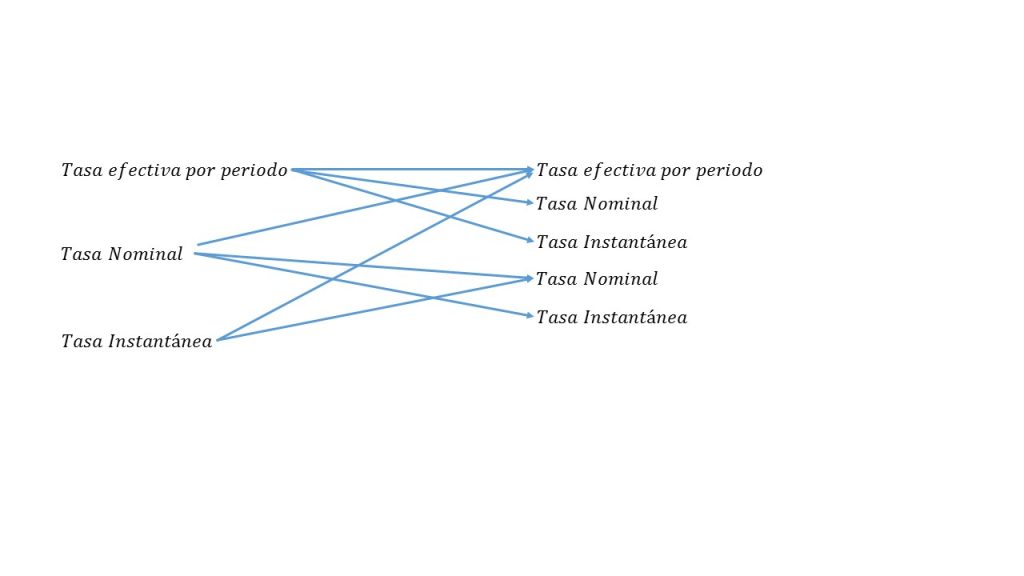
Para poder obtener tasa equivalentes hay que hacer uso del modelo de la triple igualdad
Debe cumplir que con una misma cantidad de dinero, se debe obtener el mismo monto acumulado, una vez transcurrido en el mismo tiempo, sin importar que la periodicidad de la tasa sea diferente.
Ejercicios resueltos
Ejercicio. Calcule la tasa efectiva mensual que sea equivalente a una tasa del 18% efectiva anual.
Solución
Lo que se necesita es obtener una tasa efectiva que sea equivalente a otra efectiva, con distinta periodicidad. Para hacerlo se realiza lo siguiente:
Se toma como capital inicial la cantidad de un peso, el cual lo vamos a acumular por un mes a una tasa $i$ mensual, lo cual se traduce en la siguiente expresión:
$$M=1(1+i)=(1+i)$$
Como la tasa que que nos dan es efectiva anual, y buscamos la tasa equivalente efectiva mensual que produzca el mismo monto durante un mes. Como la tasa que nos dan es anual, entonces $t$ debería ser medida en años, y se sabe que un año está formado por 12 meses, de tal forma que la variable $t=\frac{1}{12}$. Entonces tenemos la siguiente ecuación:
$$M=(1+0.18)^{\frac{1}{12}}=1.013888$$
Ahora se iguala ambas expresiones para encontrar la tasa equivalente que se quiere obtener.
$$(1+i)=1.01388$$
de dicha expresión se despeja $i$ y se obtiene:
$$i=1-1.013888=0.013888$$
Por lo tanto la tasa equivalente es del 1.1888%, la cual es la tasa efectiva mensual equivalente a 18% efectiva anual.
Comprobando la definición de tasa equivalente, se calculara el monto que producen ambas tasas con un capital de \$200 en un tiempo de 18 meses.
Primero se calcula con la tasa efectiva anual del 18%
$$200(1+0.18)^{1.5}=256.3615$$
Ahora se calcula con la tasa equivalente encontrada:
$$200(1+0.13888)^{18}=256.3615$$
Lo cual comprueba que se generan los mismos montos, por lo tanto las tasas son equivalentes.
Ejercicio. Calcule la tasa nominal pagadera 4 veces al año, es decir trimestral, equivalente a una tasa efectiva anual, del 15%
Solución
Aplicamos el mismo procedimiento:
Usando la triple igualdad se tiene:
$$M=K(1+i)^t=K\left(1+\frac{i^{(m)}}{m}\right)^{mt}$$
Luego:
$$M=1\left(1+\frac{i^{(4)}}{4}\right)^4=\left(1+\frac{i^{(4)}}{4}\right)^4$$
El monto acumulado es del 1.15% anual
$$M=(1+.15)=1.15$$
Luego, igualar ambas ecuaciones se tiene:
$$\left(1+\frac{i^{(4)}}{4}\right)^4=1.15$$
Despejamos $i^{4}
$$\left(1+\frac{i^{(4)}}{4}\right)^{\frac{4}{4}}=(1.15)^{\frac{1}{4}}$$
$$i^{4}=4((1.15)^{0.25}-1)=4(1.03555-1)=0.035558=0.142232$$
Por lo tanto, la tasa equivalente que se busca es: 14.2232%
Más adelante…
Se continuará abordando, temas de aplicación y combinación de herramientas como la que se vio en éste tema, para una mejor comprensión de la relevancia que van adquiriendo cada uno de los conceptos abordados.
Ir a Matemáticas Financieras
Entrada anterior:
Entrada siguiente:
