Si hay un Dios, es un gran matemático.
– Paul Dirac

Introducción

En la entrada anterior realizamos un desarrollo geométrico y un tanto cualitativo de un sistema de dos ecuaciones diferenciales lineales de primer orden homogéneas con coeficientes constantes con el fin de introducirnos a la teoría cualitativa de las ecuaciones diferenciales. En dicha entrada justificamos la razón por la que estudiaremos principalmente los sistemas compuestos por dos ecuaciones de primer orden.

En esta entrada presentaremos formalmente la teoría cualitativa y geométrica de los sistemas tanto lineales como no lineales compuestos por dos ecuaciones diferenciales de primer orden.

Teoría cualitativa

A lo largo del curso nos hemos centrado en el problema de obtener soluciones, hemos desarrollado una serie de métodos de resolución de ciertos tipos de ecuaciones diferenciales y sistemas lineales. Lo que haremos ahora es dar otro enfoque al estudio de las ecuaciones diferenciales planteándonos obtener información cualitativa sobre el comportamiento de las soluciones.

Hemos visto que, a medida que aumenta la complejidad de las ecuaciones diferenciales, o los sistemas lineales, mayor es la dificultad que tenemos para obtener soluciones. Existen incluso ecuaciones que no se sabe cómo se resuelven o ecuaciones en las que obtener su solución es bastante costoso, por lo que una alternativa será hacer un análisis cualitativo, pues muchas veces bastará conocer el comportamiento de las soluciones.

Recordemos que, además de hacer un análisis cualitativo, estamos interesados en hacer un análisis geométrico, así que centraremos nuestra atención en los sistemas de dos ecuaciones diferenciales ya que, como vimos en la entrada anterior, tenemos la oportunidad de hacer gráficas en dos dimensiones, es decir, podremos visualizar sin ningún problema el plano fase.

Sistemas autónomos

En la entrada anterior vimos la importancia de que el sistema no dependa explícitamente de la variable independiente $t$ para poder hacer nuestro desarrollo geométrico. Este tipo de sistemas tienen un nombre particular.

El sistema se denomina autónomo debido a que la variable independiente $t$ no aparece explícitamente en las ecuaciones del sistema. Las condiciones de $F_{1}$ y $F_{2}$ garantizan la existencia y unicidad de la solución definida $\forall$ $t \in \mathbb{R}$ del problema de valores iniciales

\begin{align*}
x^{\prime} &= F_{1}(x, y) \hspace{1.2cm} x(t_{0}) = x_{0} \\
y^{\prime} &= F_{2}(x, y), \hspace{1cm} y(t_{0}) = y_{0} \label{2} \tag{2}
\end{align*}

para cualquier $t_{0} \in \mathbb{R}$ y $(x_{0},y_{0}) \in \mathbb{R}^{2}$.

En el caso en el que tenemos una ecuación de segundo orden autónoma

$$\dfrac{d^{2}x}{dt^{2}} = f \left( x, \dfrac{dx}{dt} \right) \label{3} \tag{3}$$

Se puede convertir en un sistema autónomo introduciendo una nueva variable $y = \dfrac{dx}{dt}$, obteniendo el sistema

\begin{align*}
x^{\prime} &= y \\
y^{\prime} &= f(x, y) \label{4} \tag{4}
\end{align*}

Sistemas autónomos lineales

En el caso en el que el sistema autónomo es lineal y con coeficientes constantes, entonces lo podemos escribir como

\begin{align*}
x^{\prime} &= ax + by \\
y^{\prime} &= cx + dy \label{5} \tag{5}
\end{align*}

En donde $a, b, c$ y $d$ son constantes, $x = x(t): \mathbb{R} \rightarrow \mathbb{R}$ y $y = y(t): \mathbb{R} \rightarrow \mathbb{R}$.

Definimos las funciones $F_{1}: \mathbb{R}^{2} \rightarrow \mathbb{R}$ y $F_{2}: \mathbb{R}^{2} \rightarrow \mathbb{R}$ como

$$F_{1}(x, y) = ax + by \hspace{1cm} y \hspace{1cm} F_{2}(x, y) = cx + dy \label{6} \tag{6}$$

Podemos definir la función vectorial $F: \mathbb{R}^{2} \rightarrow \mathbb{R}^{2}$ como

$$F(x, y) = (F_{1}(x, y), F_{2}(x, y)) = (ax +by, cx +dy) \label{7} \tag{7}$$

Entonces el sistema autónomo (\ref{5}) se puede escribir como

$$Y^{\prime} = F(x, y) \label{8} \tag{8}$$

Por su puesto, si se define la matriz de coeficientes

$$\mathbf{A} = \begin{pmatrix}
a & b \\ c & d
\end{pmatrix} \label{9} \tag{9}$$

entonces el sistema lineal (\ref{5}) se puede escribir como

$$\begin{pmatrix}
x^{\prime} \\ y^{\prime}
\end{pmatrix} = \begin{pmatrix}
a & b \\ c & d
\end{pmatrix} \begin{pmatrix}
x \\ y
\end{pmatrix} \label{10} \tag{10}$$

o bien,

$$\mathbf{Y}^{\prime} = \mathbf{AY} \label{11} \tag{11}$$

como es costumbre.

Notación: Hemos visto que no necesariamente haremos uso de la notación vectorial como en la unidad anterior, así que con fines de notación usaremos letras en negrita cuando trabajemos con vectores (o matrices) y letras sin negrita cuando no usemos la notación vectorial a pesar de indicar lo mismo. Por ejemplo, la solución de un sistema en notación vectorial la escribiremos como

$$\mathbf{Y}(t) = \begin{pmatrix}
x(t) \\ y(t)
\end{pmatrix}$$

mientras que la misma solución sin notación vectorial como

$$Y(t) = (x(t), y(t))$$

Está última notación nos será de utilidad para representar coordenadas en el plano $\mathbb{R}^{2}$.

Algunas definiciones

Las siguientes definiciones son generales, para cualquier sistema autónomo de dos ecuaciones diferenciales de primer orden.

Las soluciones de un sistema autónomo reciben un nombre especial.

En la entrada anterior ya trabajamos con el plano fase, definámoslo formalmente.

Cada punto de la curva $C$ determina el estado del sistema en un instante $t$ correspondiente a una condición inicial determinada.

En la entrada anterior vimos que en cada punto $(x, y)$ de una curva solución, el vector

$$F(x, y) = (F_{1}(x, y), F_{2}(x, y))$$

es un vector tangente a dicha curva en cada punto $(x, y)$. El conjunto de vectores tangentes recibe un nombre.

Con estas definiciones podemos decir que el plano fase es una representación geométrica de todas las trayectorias de un sistema dinámico en el plano, donde cada curva representa una condición inicial diferente. Entendemos por sistema dinámico al sistema cuyo estado evoluciona con el tiempo.

Como ejemplo visualicemos el campo vectorial de dos sistemas de ecuaciones diferenciales sencillos usando la herramienta que ya conocemos.

Ejemplo: Visualizar el campo vectorial del sistema lineal

\begin{align*}
x^{\prime} &= x \\
y^{\prime} &= y
\end{align*}

Solución: La función vectorial es

$$F(x, y) = (x, y)$$

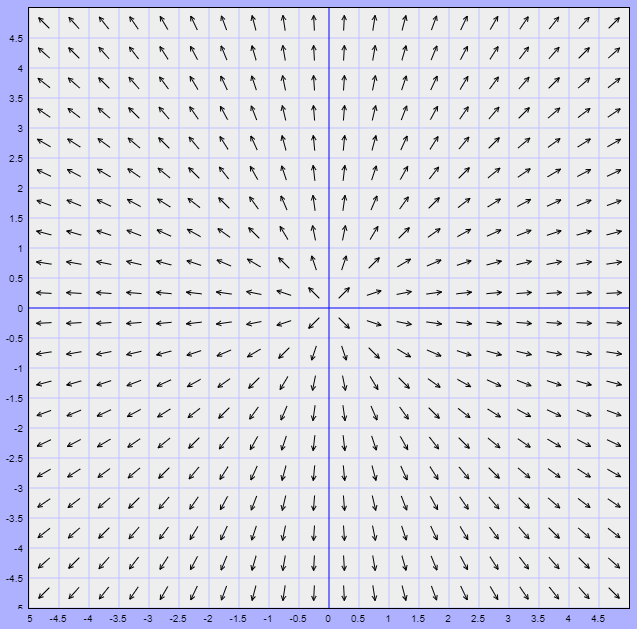
El campo vectorial en el plano fase se ilustra a continuación.

Los vectores del campo vectorial siempre señalan directamente alejándose del origen.

$\square$

Ejemplo: Visualizar el campo vectorial del sistema lineal

\begin{align*}
x^{\prime} &= -x \\
y^{\prime} &= -y
\end{align*}

Solución: La función vectorial es

$$F(x, y)= (-x, -y)$$

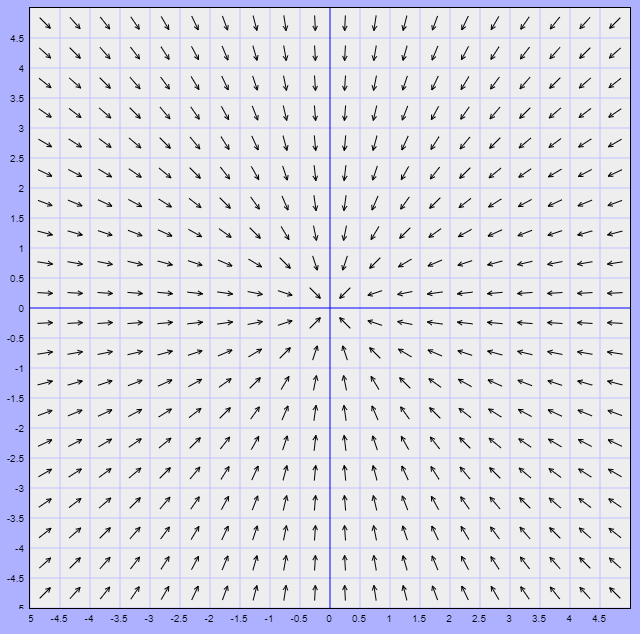
El campo vectorial se ilustra a continuación.

En este caso los vectores del campo vectorial apuntan directamente hacia el origen.

$\square$

Como el campo vectorial es tangente a las soluciones del sistema, entonces en los dos ejemplos anteriores deducimos que las soluciones son rectas con distintas pendientes para cada solución particular.

En la herramienta que utilizamos se puede dar clic sobre el campo vectorial para trazar distintas soluciones. Inténtalo con los ejemplos anteriores.

Puntos de equilibrio

Por sí solo el campo vectorial de un sistema ya nos da información sobre el comportamiento que presentan las trayectorias sin siquiera conocer explícitamente las soluciones del sistema, sin embargo en cada plano fase existe al menos un punto particular sobre el cual dependerá casi por completo el comportamiento de las soluciones, dichos puntos se conocen como puntos de equilibrio.

Una solución constante

$$Y(t) = (x(t), y(t)) = (x_{0}, y_{0}) \label{13} \tag{13}$$

para todo $t \in \mathbb{R}$ define únicamente un punto $(x_{0}, y_{0})$ en el plano fase y verifica que

$$F_{1}(x_{0}, y_{0}) = F_{2}(x_{0}, y_{0}) = 0 \label{14} \tag{14}$$

es decir,

$$F(x_{0}, y_{0}) = (0, 0) \label{15} \tag{15}$$

Como ejemplo determinemos los puntos de equilibrio de dos sistemas de ecuaciones diferenciales.

Ejemplo: Hallar los puntos de equilibrio del siguiente sistema de ecuaciones diferenciales y visualizar que ocurre alrededor de ellos.

\begin{align*}
x^{\prime} &= (x -1)(y -1) \\
y^{\prime} &= (x + 1)(y + 1)
\end{align*}

Solución: La función vectorial es

$$F(x, y) = ((x -1)(y -1), (x + 1)(y + 1))$$

Los puntos de equilibrio $(x_{0}, y_{0})$ son tales que

$$F(x_{0},y_{0}) = (0, 0)$$

es decir, tales que

$$((x_{0} -1)(y_{0} -1), (x_{0} + 1)(y_{0} + 1)) = (0, 0)$$

El sistema de ecuaciones que se forma es

\begin{align*}
(x_{0} -1) (y_{0} -1) &= 0 \\
(x_{0} + 1) (y_{0} + 1) &= 0
\end{align*}

Los puntos que verifican el sistema son

$$(x_{0}, y_{0}) = (1, -1) \hspace{1cm} y \hspace{1cm} (x_{0}, y_{0}) = (-1, 1)$$

Hemos encontrado dos puntos de equilibrio. Veamos cómo se ve el campo vectorial del sistema y que forma tienen las soluciones alrededor de estos puntos.

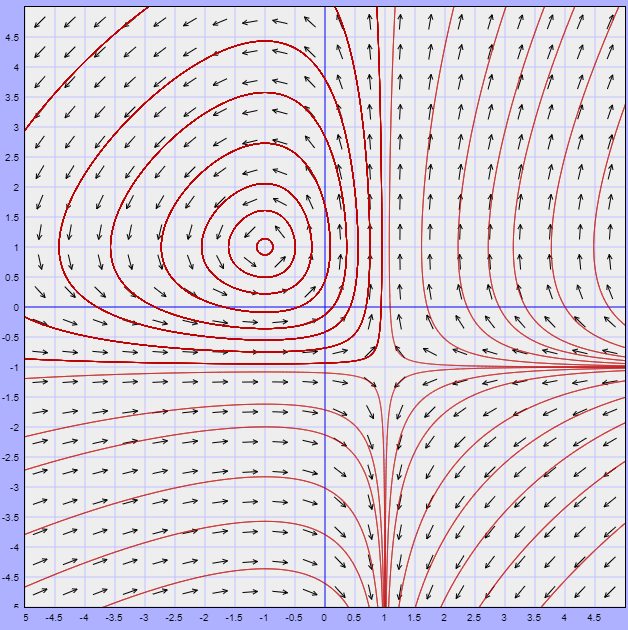
Recordemos que la dirección de las trayectorias está definida por la dirección del campo vectorial. En el plano fase observamos que alrededor del punto de equilibrio $(-1, 1)$ las soluciones son trayectorias cerradas que giran en torno a dicho punto, mientras que alrededor del punto de equilibrio $(1, -1)$ las trayectorias tienden a acercarse a dicho punto, pero cuando se aproximan a él inmediatamente se alejan.

$\square$

Más adelante caracterizaremos a los puntos de equilibrio de acuerdo al tipo de comportamiento que tienen las trayectorias alrededor de él. Por ahora notemos estas características. Veamos un ejemplo más.

Ejemplo: Hallar los puntos de equilibrio del siguiente sistema de ecuaciones diferenciales y visualizar que ocurre alrededor de ellos.

\begin{align*}
x^{\prime} &= x^{2} -1 \\
y^{\prime} &= -y
\end{align*}

Solución: La función vectorial es

$$F(x, y) = (x^{2} -1, -y)$$

Si

$$F(x_{0}, y_{0}) = (0,0)$$

entonces,

$$(x^{2}_{0} -1, -y_{0}) = (0, 0)$$

El sistema de ecuaciones que se obtiene es

\begin{align*}
x^{2}_{0} -1 &= 0 \\
-y_{0} &= 0
\end{align*}

De la segunda ecuación obtenemos inmediatamente que $y_{0} = 0$ y de la primer ecuación obtenemos que $x^{2}_{0}= 1$. Por lo tanto, los puntos de equilibrio son

$$(x_{0}, y_{0}) = (-1, 0) \hspace{1cm} y \hspace{1cm} (x_{0}, y_{0}) = (1, 0)$$

Veamos cómo se ve el plano fase.

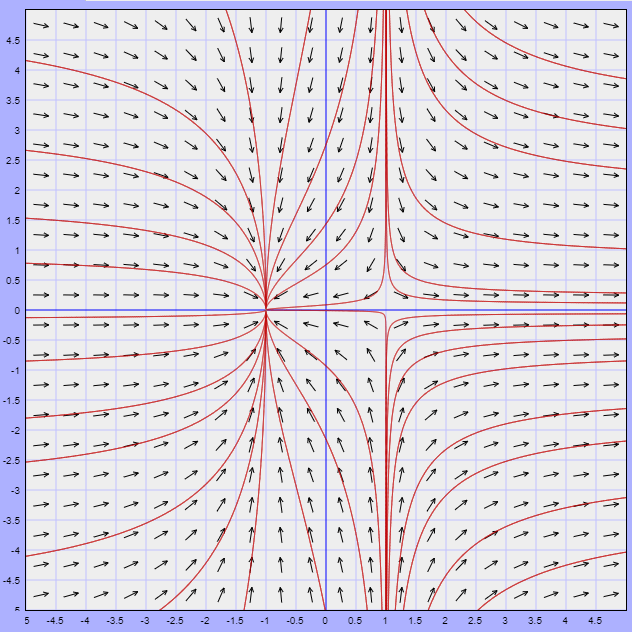
En esta ocasión observamos que las trayectorias tienden hacía el punto de equilibrio $(-1, 0)$, mientras que alrededor del punto de equilibrio $(1, 0)$ las trayectorias tienden a alejarse de él.

$\square$

Con estos dos ejemplos observamos tres cualidades de las trayectorias alrededor de los puntos de equilibrio. El primero de ellos es que hay trayectorias cerradas que permanecen cerca de un punto de equilibrio, pero que nunca llegan a él, por otro lado, hay trayectorias que tienden directamente hacía a un punto de equilibrio y finalmente hay puntos de equilibrio en los que las trayectorias tienden a alejarse de él. A esto se le conoce como estabilidad de los puntos de equilibrio y lo estudiaremos más adelante en esta entrada.

Un hecho importante es que los sistemas de los dos ejemplos anteriores son sistemas no lineales y ya comenzamos a caracterizar y visualizar el comportamiento de las soluciones a pesar de no conocer ningún método para obtener las soluciones explícitamente, de ahí la importancia de este análisis cualitativo.

Cabe mencionar que resolver sistemas no lineales puede ser muy complejo, al menos para un primer curso de ecuaciones diferenciales, es por ello que dedicamos la unidad anterior al caso exclusivamente lineal.

Por otro lado, es claro que cada punto del plano fase, o bien es un punto de equilibrio, o bien pasa por él una única trayectoria. Existe un resultado importante que nos permite saber cuando el único punto de equilibrio de un sistema lineal es el origen.

Demostración: Consideremos el sistema lineal ${\mathbf{Y}}’ = \mathbf{AY}$ cuya matriz de coeficientes es (\ref{9}), entonces podemos escribir al sistema lineal como

$$\begin{pmatrix}
x^{\prime} \\ y^{\prime}
\end{pmatrix} = \begin{pmatrix}
a & b \\ c & d
\end{pmatrix} \begin{pmatrix}
x \\ y
\end{pmatrix}$$

Sabemos que un punto $Y_{0} = (x_{0}, y_{0})$ es un punto de equilibrio del sistema si el campo vectorial en $Y_{0}$ es cero, es decir, si

$$F(x_{0}, y_{0}) = (0, 0)$$

Sabemos, por otro lado, que el sistema lineal también se puede escribir en términos de la función vectorial $F$ como

$$F(x, y) = (F_{1}(x, y), F_{2}(x, y)) = (ax + by, cx + dy)$$

Entonces $Y_{0} = (x_{0}, y_{0})$ es un punto de equilibrio si ocurre que

$$F(x_{0}, y_{0}) = (ax_{0} + by_{0}, cx_{0} + dy_{0}) = (0, 0) \label{16} \tag{16}$$

es decir, debe ocurrir que

$$\begin{pmatrix}
a & b \\ c & d
\end{pmatrix} \begin{pmatrix}
x_{0} \\ y_{0}
\end{pmatrix} = \begin{pmatrix}
ax_{0} + by_{0} \\ cx_{0} + dy_{0}
\end{pmatrix} = \begin{pmatrix}
0 \\ 0
\end{pmatrix} \label{17} \tag{17}$$

El par de ecuaciones que se tiene es

\begin{align*}
ax_{0} + by_{0} &= 0 \\
cx_{0} + dy_{0} &= 0 \label{18} \tag{18}
\end{align*}

Es claro que $(x_{0}, y_{0}) = (0, 0)$ es una solución de las ecuaciones (\ref{18}). Por tanto, $Y_{0} = (0, 0)$ es un punto de equilibrio y la función constante

$$Y(t) = (0, 0) \label{19} \tag{19}$$

para toda $t \in \mathbb{R}$ es una solución del sistema lineal. Ahora veamos si existe otra solución que no sea la trivial.

Cualesquiera puntos de equilibrio $(x_{0}, y_{0}) \neq (0, 0)$ deben también satisfacer el sistema (\ref{18}). Para encontrarlos supongamos por ahora que $a\neq 0$, de la primer ecuación se obtiene que

$$x_{0} = -\dfrac{b}{a}y_{0} \label{20} \tag{20}$$

Sustituyendo en la segunda ecuación, se tiene

$$c \left( -\dfrac{b}{a} \right) y_{0} + dy_{0} = 0$$

que puede escribirse como

$$(ad -bc)y_{0} = 0 \label{21} \tag{21}$$

Entonces,

$$y_{0} = 0 \hspace{1cm} o \hspace{1cm} ad -bc =0$$

Si $y_{0} = 0$, entonces $x_{0} = 0$ y de nuevo obtenemos la solución trivial. Por tanto, un sistema lineal tiene puntos de equilibrio no triviales sólo si

$$ad -bc = 0$$

es decir si el determinante de $\mathbf{A}$ es igual a cero. Esto significa que si $|\mathbf{A}| \neq 0$, entonces el único punto de equilibrio del sistema lineal es el origen.

$\square$

Una observación importante en la demostración es que el cálculo que hicimos no depende de los valores de los coeficientes $a, b, c$ y $d$, sólo de la condición $a \neq 0$, por tanto ¡todo sistema lineal tiene un punto de equilibrio en el origen!.

Estabilidad de puntos de equilibrio

Veíamos que hay tres cualidades de las trayectorias alrededor de puntos de equilibrio. De acuerdo al comportamiento que tengan las trayectorias alrededor de los puntos de equilibrio éstos recibirán un nombre.

Lo que esta definición nos dice es que si una trayectoria está cerca del punto de equilibrio $(x_{0}, y_{0})$, entonces se mantendrá cerca de él para $t_{0} \leq t \rightarrow \infty$.

Es este caso las trayectorias cercanas al punto de equilibrio $(x_{0}, y_{0})$ no sólo se mantendrán cerca de dicho punto, sino que tenderán a él para $t_{0} \leq t \rightarrow \infty$.

Contrario a un punto de equilibrio estable, si las trayectorias están cerca del punto de equilibrio $(x_{0}, y_{0})$, entonces se alejarán de él para $t_{0} \leq t \rightarrow \infty$.

Las definiciones anteriores son aplicables a cualquier punto de equilibrio $(x_{0}, y_{0})$, sin embargo las definiciones se vuelven más intuitivas si el punto de equilibrio sobre el que se trabaja es el origen $(x_{0}, y_{0}) = (0, 0)$ del plano $XY$ o plano fase.

Supongamos que el punto de equilibrio del sistema (\ref{1}) es el origen y que está aislado, esto es que existe un entorno donde no hay otro punto de equilibrio. Notemos que el hecho de que el punto de equilibrio sea el origen no supone ningún tipo de restricción ya que se puede hacer el cambio de variable

\begin{align*}
\hat{x} &= x -x_{0} \\
\hat{y} &= y -y_{0} \label{24} \tag{24}
\end{align*}

y transformar al sistema (\ref{1}) en

\begin{align*}
\hat{x}^{\prime} &= F(\hat{x} + x_{0}, \hat{y} + y_{0}) \\
\hat{y}^{\prime} &= G(\hat{x} + x_{0}, \hat{y} + y_{0}) \label{25} \tag{25}
\end{align*}

cuyo punto de equilibrio es el punto $(0, 0)$. En estas condiciones definimos de manera más intuitiva la estabilidad de un punto de equilibrio.

Realicemos algunos ejemplos de manera gráfica.

Ejemplo: Definir el tipo de punto de equilibrio del siguiente sistema visualizando el comportamiento de las trayectorias alrededor de dicho punto.

\begin{align*}
x^{\prime} &= 5y \\
y^{\prime} &= -2x
\end{align*}

Solución: Es claro que el punto de equilibrio es el origen ya que si $x = 0$ y $y = 0$, entonces

$$F(0, 0) = (0, 0)$$

El campo vectorial y algunas trayectorias del sistema se muestran a continuación.

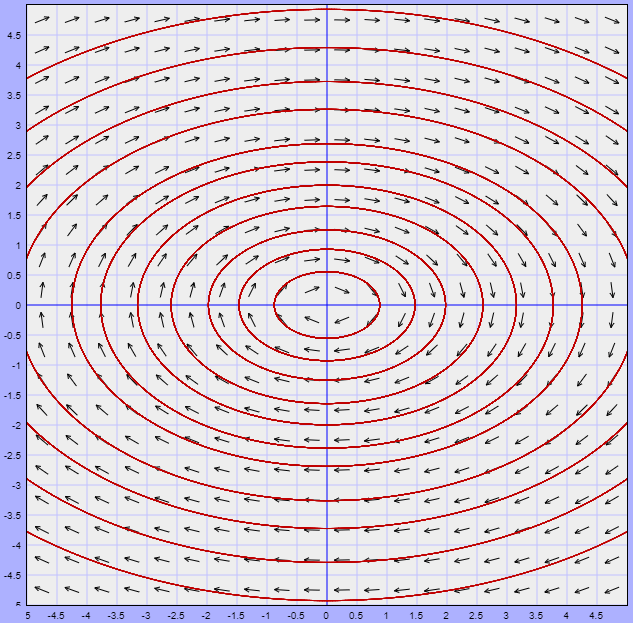
Observamos que las trayectorias son cerradas, lo que significa que todas las que están cerca del punto de equilibrio permanecerán cerca de él, pero nunca llegarán a él conforme $t \rightarrow \infty$. De acuerdo a las definiciones anteriores, el punto de equilibrio corresponde a un punto estable. Veremos más adelante que este tipo de trayectorias corresponden a soluciones periódicas.

$\square$

Ejemplo: Definir el tipo de punto de equilibrio del siguiente sistema visualizando el comportamiento de las trayectorias alrededor de dicho punto.

\begin{align*}
x^{\prime} &= -3x -4y \\
y^{\prime} &= 2x + y
\end{align*}

Solución: Como el sistema es lineal podemos aplicar el teorema visto para verificar que el único punto de equilibrio del sistemas es el origen. La matriz de coeficientes es

$$\mathbf{A} = \begin{pmatrix}
-3 & -4 \\ 2 & 1
\end{pmatrix} $$

Calculemos el determinante.

$$\begin{vmatrix}
-3 & -4 \\ 2 & 1
\end{vmatrix} = -3 + 8 = 5 \neq 0$$

Como $|A| \neq 0$, entonces el único punto de equilibrio es el origen.

El plano fase del sistema se ilustra a continuación.

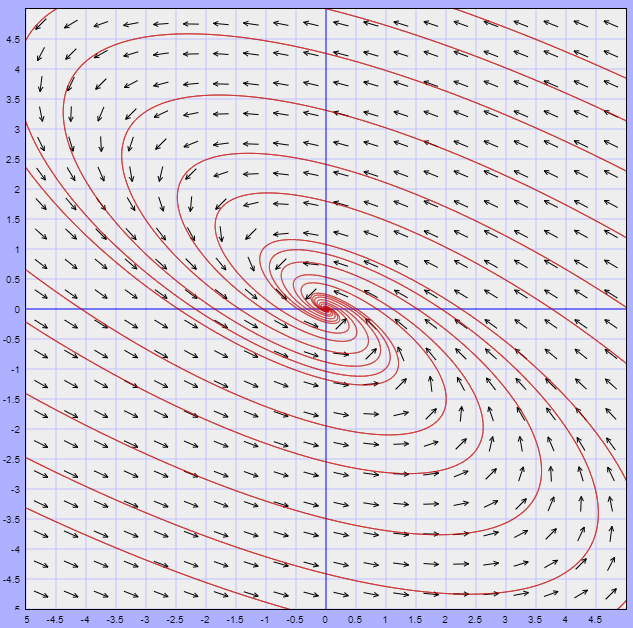
Es este caso se logra observar que las trayectorias cerca del punto de equilibrio tienden a él conforme $t \rightarrow \infty$, lo que lo define como un punto de equilibrio asintóticamente estable.

$\square$

Veamos un último ejemplo.

Ejemplo: Definir el tipo de punto de equilibrio del siguiente sistema visualizando el comportamiento de las trayectorias alrededor de dicho punto.

\begin{align*}
x^{\prime} &= 5x -2y \\
y^{\prime} &= 2x -3y
\end{align*}

Solución: Nuevamente se puede verificar que el único punto de equilibrio del sistema es el origen. Observemos el plano fase.

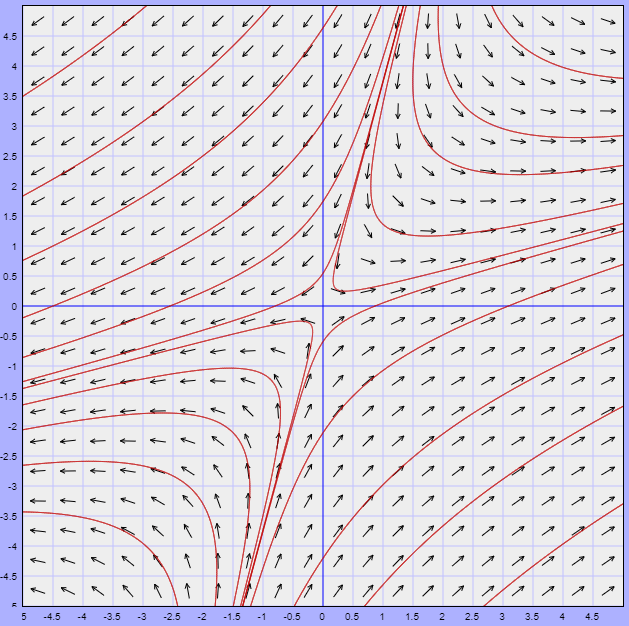
En este caso se observa que cerca del punto de equilibrio las trayectorias se alejan de él, por lo que dicho punto es un punto inestable.

$\square$

Al menos geométricamente ya somos capaces de identificar el tipo de comportamiento que tienen las trayectorias alrededor de los puntos de equilibrio según su clasificación.

Más adelante resolveremos algunos sistemas lineales y haremos este mismo análisis desde una perspectiva analítica analizando las soluciones que obtengamos. Más aún, veremos que de acuerdo al valor de los eigenvalores del sistema será el tipo de punto de equilibrio que tendrá dicho sistema. Pero antes de ello, en la siguiente entrada estudiemos algunas propiedades cualitativas de las trayectorias.

Tarea moral

Los siguientes ejercicios no forman parte de la evaluación del curso, pero servirán para entender mucho mejor los conceptos vistos en esta entrada, así como temas posteriores.

1. Visualizar el campo vectorial y algunas trayectorias de los siguientes sistemas. ¿Tienen puntos de equilibrio?.

• $x^{\prime} = (y -x)(y -1)$
  $y^{\prime} = (x- y)(x -1)$

• $x^{\prime} = -y(y -2)$
  $y^{\prime} = (x -2)(y -2)$

2. Determinar los puntos de equilibrio de los siguientes sistemas y clasificarlos como estables, asintóticamente estables o inestables. Visualizar el campo vectorial y algunas trayectorias.

• $x^{\prime} = 2y$
  $y^{\prime} = 2x$

• $x^{\prime} = -8y$
  $y^{\prime} = 18x$

• $x^{\prime} = 2x + y + 3$
  $y^{\prime} = -3x -2y -4$

• $x^{\prime} =-5x + 2y$
  $y^{\prime} = x -4y$

• $x^{\prime} = 2x + 13y$
  $y^{\prime} = -x -2y$

• $x^{\prime} = x(7 -x -2y)$
  $y^{\prime} = y(5 -x -y)$

3. Analizar el comportamiento de las curvas solución del siguiente sistema.

• $x^{\prime} = 3/y$
  $y^{\prime} = 2/x$
  
  ¿Qué se puede observar?. ¿Hay puntos de equilibrio?.

Más adelante…

Conforme avanzamos nos damos cuenta que es posible describir cualitativamente las soluciones de un sistema tanto lineal como no lineal compuesto por dos ecuaciones diferenciales de primer orden homogéneas con coeficientes contantes, esto tiene la enorme ventaja de que ya no es necesario conocer explícitamente las soluciones del sistema para poder trabajar.

Continuando con nuestro desarrollo cualitativo, en la siguiente entrada estudiaremos algunas propiedades de las trayectorias en el plano fase.

Entradas relacionadas

• Página principal del curso: Ecuaciones Diferenciales I
• Entrada anterior del curso: Introducción a la teoría cualitativa de las ecuaciones diferenciales
• Siguiente entrada del curso: Propiedades cualitativas de las trayectorias

• Video relacionado al tema: Geometría de las soluciones a un sistema de dos ecuaciones de primer orden, plano fase y campo vectorial asociado
• Video relacionado al tema: Puntos de equilibrio y estabilidad para sistemas de dos ecuaciones de primer orden

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»