Introducción
En la entrada anterior vimos la definición de la integral para funciones complejas de variable real, es decir, funciones híbridas. Aunque de cierta manera esta definición nos limita, ya que en general trabajamos con funciones complejas de variable compleja.
Al igual que sucedió con el concepto de diferenciabilidad para una función compleja de variable compleja, también existe el concepto de integrabilidad para funciones complejas. En esta entrada veremos que aunque muchas de las definiciones y resultados para este tipo de integrales son una extensión de los conceptos de integración para funciones de varias variables reales, vistos en nuestros cursos de Cálculo, la integración en el sentido complejo va más allá de un simple salto de los resultados para funciones reales a la variable compleja, ya que como veremos, a través de la integración compleja es posible obtener herramientas e ideas únicas para el estudio de la teoría de las funciones complejas.
Definición 34.1. (Integral de contorno o integral de línea compleja.)
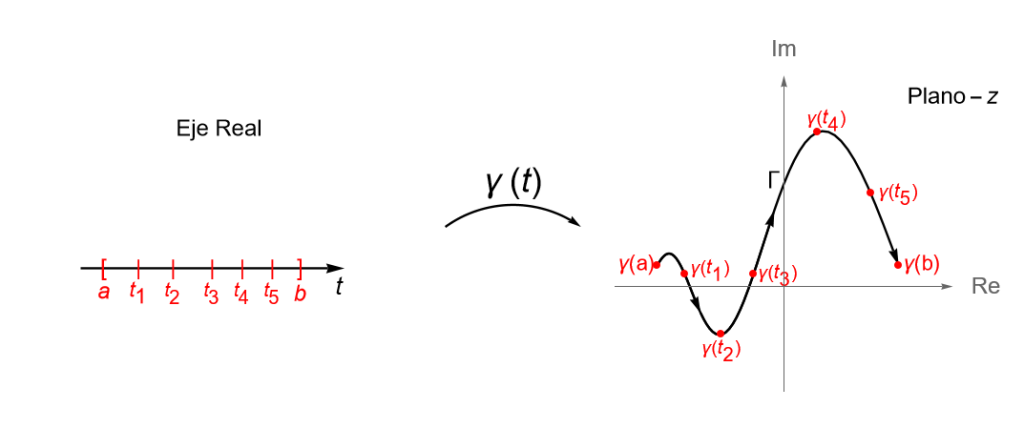
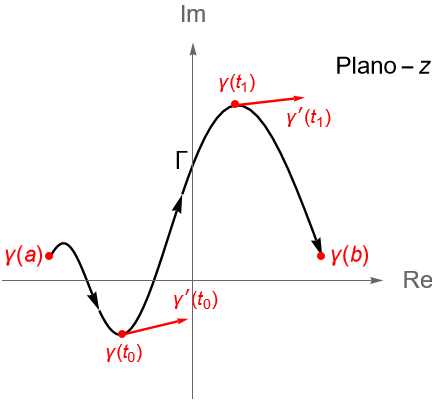
Sean $U\subset\mathbb{C}$ un conjunto abierto, $[a,b]\subset\mathbb{R}$, con $a<b$ un intervalo cerrado, $f: U \to \mathbb{C}$ una función continua en $U$ y $\gamma:[a,b] \to U$ un contorno en $U$ (definición 32.9). Se define a la integral de contorno o integral de línea compleja, a lo largo de $\gamma$, como:
\begin{equation*}
\int_{\gamma} f(z) dz := \int_{a}^{b} f(\gamma(t)) \gamma'(t)dt.\tag{34.1}
\end{equation*}
Si $C$ denota al contorno dado por la trayectoria $\gamma$, entonces la integral en (34.1) se puede escribir como:
\begin{equation*}
\int_{C} f(z) dz.
\end{equation*}
Observación 34.1.
Recordemos que un contorno es una trayectoria $\gamma$ de clase $C^1$ o de clase $C^1$ a trozos, por lo que al igual que con las integrales de funciones híbridas, esta definición ya considera el caso en el que $\gamma$ sea una curva suave a trozos. En tal caso, para la partición:
\begin{equation*}
P : a=t_0 < t_1 < \cdots < t_{n-1}<t_n=b,
\end{equation*}del intervalo $[a,b]$, tal que $\gamma_k$, la restricción de $\gamma$ al intervalo $[t_{k-1}, t_k]$, es una curva suave para $1\leq k\leq n$, entonces:
\begin{equation*}
\int_{\gamma} f(z) dz = \int_{\gamma_1} f(z) dz + \cdots + \int_{\gamma_n} f(z) dz = \sum_{k=1}^n \int_{\gamma_k} f(z) dz. \tag{34.2}
\end{equation*}
Observación 34.2.
Si $f(z) = u(z)+iv(z)$ y $\gamma(t)=\gamma_1(t)+i\gamma_2(t)$, tenemos que:
\begin{align*}
f(\gamma(t)) \gamma'(t) & = \left[u(\gamma(t))+iv(\gamma(t))\right]\left[\gamma_1 ‘(t)+i\gamma_2′(t)\right]\\
& = u(\gamma(t)) \gamma_1 ‘(t) – v(\gamma(t)) \gamma_2′(t) + i \left[u(\gamma(t)) \gamma_2 ‘(t) + v(\gamma(t)) \gamma_1′(t)\right],
\end{align*}por lo que la función híbrida $g(t)= f(\gamma(t)) \gamma'(t)$ es continua (o continua a trozos) en $[a,b]$, entonces la integral del lado derecho en (34.1) está bien definida.
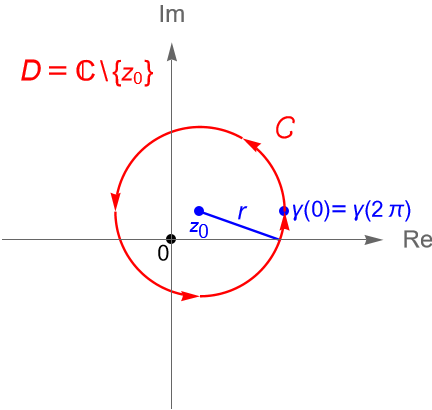
Ejemplo 34.1.
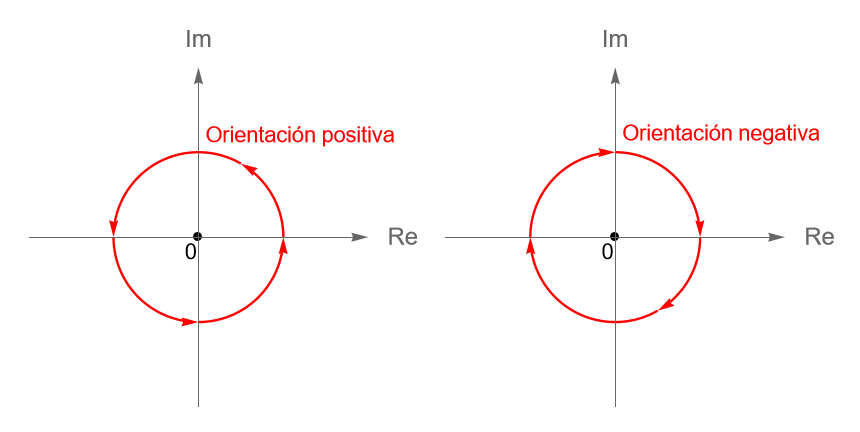
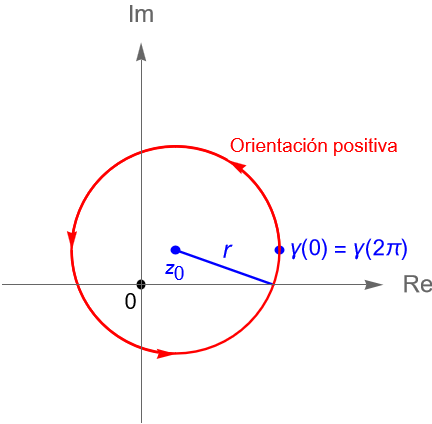
Sea $C$ el contorno dado por la circunferencia $C(z_0, r)$, con $r>0$ y $z_0\in\mathbb{C}$ fijo, orientada positivamente.
a) Veamos que:
\begin{equation*}
\int_{C} \frac{1}{z-z_0} dz = i 2\pi.
\end{equation*}
b) Si $n\in\mathbb{Z}$ es tal que $n\neq1$, veamos que:
\begin{equation*}
\int_{C} \frac{1}{(z-z_0)^n} dz = 0.
\end{equation*}
Solución. Primeramente, podemos parametrizar al contorno $C$ mediante la trayectoria $\gamma(t)=z_0 + re^{it}$, con $0\leq t\leq 2\pi$. Por la proposición 32.1(1) y el ejemplo 32.1 tenemos que $\gamma'(t)=ire^{it}$.
Sea $D := \mathbb{C}\setminus\{z_0\}$. Claramente $C$ es un contorno en $D$.
a) Sea $f(z)=\dfrac{1}{z-z_0}$. Dado que $f$ es una función racional, entonces es analítica en el dominio $D$ y por tanto continua en $D$.
De acuerdo con la definición 34.1, tenemos que:
\begin{align*}
\int_{C} \frac{1}{z-z_0} dz & = \int_{0}^{2\pi} f(\gamma(t)) \gamma'(t)dt\\
& = \int_{0}^{2\pi} \frac{1}{z_0 +re^{it} – z_0} ire^{it} dt\\
& = \int_{0}^{2\pi} i dt\\
& = i 2\pi.
\end{align*}
b) Sean $n\in\mathbb{Z}$ tal que $n\neq1$ y $f(z)=\dfrac{1}{(z-z_0)^n}$. Análogamente tenemos que la función racional $f$ es continua en $D$.
Considerando la definición 34.1, el ejemplo 32.1 y las proposiciones 33.1(3), 33.2, 20.2(2) y 20.2(10), tenemos que:
\begin{align*}
\int_{C} \frac{1}{(z-z_0)^n} dz & = \int_{0}^{2\pi} f(\gamma(t)) \gamma'(t)dt\\
%& = \int_{0}^{2\pi} \frac{1}{(z_0 +re^{it} – z_0)^n} ire^{it} dt\\
& = ir^{1-n} \int_{0}^{2\pi} e^{it(1-n)} dt\\
& = ir^{1-n} \left. \frac{e^{it(1-n)}}{i(1-n)} \right|_{0}^{2\pi}\\
& = \frac{r^{1-n}}{1-n} \left(e^{i2\pi(1-n)} – e^{0}\right)\\
& = \frac{r^{1-n}}{1-n} \left(1 – 1\right)\\
& = 0.
\end{align*}
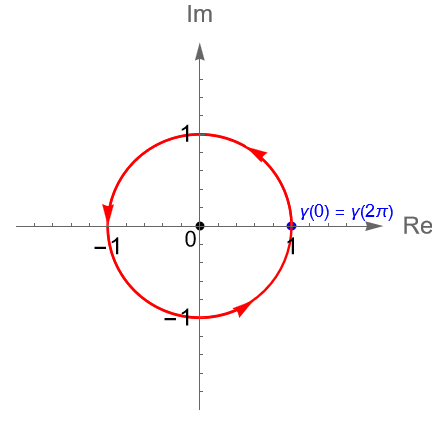
En particular, si $C$ es la circunferencia unitaria, orientada positivamente, es decir, dada por la trayectoria $\gamma(t)=e^{it}$, con $0\leq t\leq 2\pi$, entonces se cumple que:
\begin{equation*}
\int_{C} \frac{1}{z} dz = \int_{C(0,1)} \frac{1}{z} dz = 2\pi i.
\end{equation*}
Ejemplo 34.2.
De acuerdo con los ejemplos 32.1, 33.2 y las proposiciones 20.2(2) y 33.1(3), para el contorno $C$ dado por la circunferencia unitaria, orientada positivamente, es decir, $\gamma(t)=e^{it}$, con $0\leq t\leq 2\pi$, tenemos que:
\begin{align*}
\int_{C(0,1)} z^{n} dz & = \int_{0}^{2\pi} e^{itn} i e^{it} dt\\
& = i \int_{0}^{2\pi} e^{it(n+1)} dt\\
& = \left\{ \begin{array}{lcc}
0 & \text{si} & n \neq -1, \\ \\
i2\pi & \text{si} & n=-1.
\end{array} \right.
\end{align*}para todo $n\in\mathbb{Z}$.
Ejemplo 34.3.
Sea $C$ el contorno dado por la circunferencia $C(0, 1)$, orientada positivamente. Veamos que:
\begin{equation*}
\int_{C} \frac{1}{\overline{z}} dz = 0 \quad \text{y} \quad \int_{C} \overline{z} dz = i2\pi.
\end{equation*}
Solución. Podemos parametrizar a $C$ como la trayectoria $\gamma(t)=e^{it}$, con $0\leq t\leq 2\pi$, por lo que $\gamma'(t)=ie^{it}$.
Por la proposición 20.2(8) tenemos que $\overline{e^{it}} = e^{\overline{it}} = e^{-it}$, entonces, de acuerdo con la definición 34.1, el ejemplo 33.2 y las proposiciones 20.2(2), 20.2(3) y 33.1(3), tenemos que:
\begin{align*}
\int_{C(0,1)} \frac{1}{\overline{z}} dz & = \int_{0}^{2\pi} \frac{1}{\overline{e^{it}}} i e^{it} dt\\
& = \int_{0}^{2\pi} \frac{1}{e^{-it}} i e^{it} dt\\
& = i \int_{0}^{2\pi} e^{i2t} dt\\
& = i \cdot 0\\
& = 0.
\end{align*}
\begin{align*}
\int_{C(0,1)}\overline{z} dz & = \int_{0}^{2\pi} \overline{e^{it}} i e^{it} dt\\
& = \int_{0}^{2\pi} e^{-it} i e^{it} dt\\
& = i \int_{0}^{2\pi} 1 dt\\
& = i 2\pi.
\end{align*}
Ejemplo 34.4.
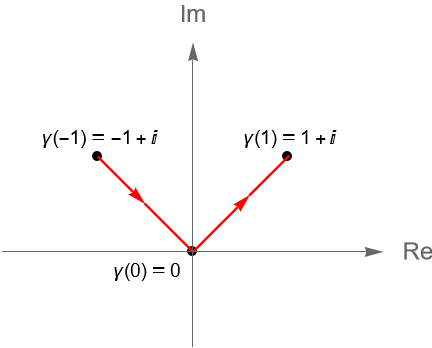
Evaluemos la integral $\int_{\gamma} (x+y) dz$ a lo largo del contorno $\gamma=[0,1+i]+[1+i, i]$.
Solución. De acuerdo con el ejemplo 15.1, es claro que para $z=x+iy\in\mathbb{C}$ la función $f(z)=\operatorname{Re}(z)+\operatorname{Im}(z)$ es una función continua en $\mathbb{C}$. Notemos que el contorno dado por la trayectoria $\gamma$ es una curva suave a trozos. Por el ejemplo 32.2 tenemos que:
\begin{equation*}
[0,1+i](t) = (1+i)t, \quad [1+i,i](t) = 1+i -t, \quad \forall t\in[0,1].
\end{equation*}
De acuerdo con la definición 32.13, tenemos que:
\begin{equation*}
\gamma(t) : = \left( [0,1+i] + [1+i,i] \right)(t) = \left\{ \begin{array}{lcc} (1+i)t & \text{si} & 0 \leq t \leq 1, \\ \\
2-t+i & \text{si} & 1 \leq t \leq 2. \end{array} \right.
\end{equation*}
Es claro que las curvas $\gamma_1 = \left. \gamma\right|_{[0,1]}$ y $\gamma_2 = \left. \gamma\right|_{[1,2]}$ son suaves, cuyas derivadas son, respectivamente, $\gamma_1′(t) = 1+i$ y $\gamma_2′(t) = -1$.
Entonces, por (34.2), (34.1) y las proposiciones 33.1 y 33.2, se tiene que:
\begin{align*}
\int_{\gamma} (x+y) dz & = \int_{\gamma_1} (x+y) dz + \int_{\gamma_2} (x+y) dz\\
& = \int_{0}^{1} 2t(1+i) dt + \int_{1}^{2} (3-t)(-1) dt\\
&= \left.(1+i)t^2\right|_{0}^{1} – \left.\left[3t – \frac{t^2}{2}\right]\right|_{1}^{2}\\
& = -\frac{1}{2} + i.
\end{align*}
Observación 34.3.
Considerando la definición 33.1 y el producto interior de $\mathbb{R}^2$, tenemos que:
\begin{align*}
\int_{\gamma} f(z) dz & = \int_{a}^{b} f(\gamma(t)) \gamma'(t) dt\\
& = \int_{a}^{b} \left[u(\gamma(t)) \gamma_1 ‘(t) – v(\gamma(t)) \gamma_2′(t)\right] dt + i \int_{a}^{b} \left[v(\gamma(t)) \gamma_1′(t) + u(\gamma(t)) \gamma_2 ‘(t)\right] dt\\
& = \int_{a}^{b} \left(u(\gamma(t)), -v(\gamma(t))\right) \cdot \left(\gamma_1 ‘(t), \gamma_2′(t)\right) dt + i \int_{a}^{b} \left(v(\gamma(t)), u(\gamma(t))\right) \cdot \left( \gamma_1′(t), \gamma_2 ‘(t)\right) dt.
\end{align*}
Si definimos a los campos vectoriales, en el plano, $F, G: U\subset\mathbb{R}^2 \to \mathbb{R}^2$ dados, respectivamente, por:
\begin{equation*}
F(x,y)=(u(x,y), -v(x,y)) \quad \text{y} \quad G(x,y)=(v(x,y), u(x,y)),
\end{equation*}entonces:
\begin{align*}
\int_{\gamma} f(z) dz & = \int_{a}^{b} F(\gamma(t)) \cdot \gamma'(t) dt + i \int_{a}^{b} G(\gamma(t)) \cdot \gamma'(t) dt\\
& = \int_\Gamma F \cdot d\gamma + i \int_\Gamma G \cdot d\gamma,
\end{align*}donde $\Gamma=\gamma([a,b])$. Es decir, la interal que definimos en 34.1 se puede expresar en términos de la integral de línea de dos campos vectoriales en $\mathbb{R}^2$.
En este punto es conveniente recordar el siguiente resultado de Cálculo.
Teorema 34.1. (Cambio de variable.)
Sean $[a,b], [c,d]\subset\mathbb{R}$, con $a<b$ y $c<d$, dos intervalos cerrados, $f: [a,b] \to \mathbb{R}$ y $g: [c,d] \to \mathbb{R}$ dos funciones tales que $g([c,d])\subseteq [a,b]$, $f$ es continua en $[a,b]$ y $g$ de clase $C^1$ en $[c,d]$, entonces:
\begin{equation*}
\int_{c}^{d} f(g(t)) g'(t) dt = \int_{g(c)}^{g(d)} f(t)dt.
\end{equation*}
Una consecuencia del resultado anterior es la siguiente:
Proposición 34.1. (Independencia de la parametrización.)
Sean $U\subset\mathbb{C}$ un conjunto abierto, $[a,b], [c,d]\subset\mathbb{R}$, con $a<b$ y $c<d$, dos intervalos cerrados, $f: U \to \mathbb{C}$ una función continua en $U$ y $\gamma_1:[a,b] \to U$ un contorno en $U$. Si $\gamma_2:[c,d] \to U$ es una reparametrización de $\gamma_1$, entonces:
\begin{equation*}
\int_{\gamma_1} f(z) dz = \int_{\gamma_2} f(z) dz.
\end{equation*}
Demostración. Dadas las hipótesis, tenemos que existe una biyección $\sigma:[c,d]\to[a,b]$ continua de clase $C^1$ tal que $\sigma$ es creciente y $\gamma_2=\gamma_1\circ \sigma$.
Entonces, de acuerdo con la observación 34.2, la definición 34.1, el teorema 34.1 y la regla de la cadena, para $s=\sigma(t)$ tenemos que:
\begin{align*}
\int_{\gamma_2} f(z) dz & = \int_{c}^{d} f(\gamma_2(t)) \gamma_2′(t)dt\\
& = \int_{c}^{d} f(\gamma_1(\sigma(t))) \gamma_1′(\sigma(t)) \sigma'(t)dt\\
& = \int_{\sigma(c)}^{\sigma(d)} f(\gamma_1(s)) \gamma_1′(s) ds\\
& = \int_{a}^{b} f(\gamma_1(s)) \gamma_1′(s) ds\\
& = \int_{\gamma_1} f(z) dz.
\end{align*}
$\blacksquare$
Ejemplo 34.5.
Determinemos el valor de la integral:
\begin{equation*}
\int_{C} \frac{dz}{z-2},
\end{equation*}donde $C$ es la semicircunferencia superior de radio $r=1$ y centro en $z_0=2$.
Solución. Es claro que $C$ es un contorno ya que la trayectoria $\gamma(t)=2+e^{i\pi}$, con $0\leq t\leq \pi$, que lo parametriza, es una curva suave.
De acuerdo con el ejemplo 34.1, inferimos que el valor de dicha integral es $i\pi$. Procedemos a verificar lo anterior utilizando la proposición 34.1, es decir, considerando otra parametrización para el contorno $C$.
De acuerdo con el ejemplo 32.13(b), sabemos que $\beta(t)=2+e^{i\pi t}$, con $0\leq t \leq 1$, es una reparametrización de la curva $\gamma$.
Entonces, por la definición 34.1 tenemos que:
\begin{align*}
\int_{C} \frac{1}{z-2} dz & =\int_{0}^{1} f(\beta(t)) \beta'(t)dt\\
& = \int_{0}^{1} \frac{1}{2 +e^{i\pi t} – 2} i\pi e^{i\pi t} dt\\
& = \int_{0}^{1} i\pi dt\\
& = i\pi.
\end{align*}
Al igual que con las integrales de funciones híbridas, las integrales de contorno cumplen algunas propiedades que resultan de utilidad al resolver ciertos problemas.
Proposición 34.2. (Propiedades integrales de contorno.)
Sean $U\subset\mathbb{C}$ un conjunto abierto, $[a,b]\subset\mathbb{R}$, con $a<b$ un intervalo cerrado, $f, g: U \to \mathbb{C}$ dos funciones continuas en $U$ y $\gamma:[a,b] \to U$ un contorno en $U$. Se cumplen las siguientes propiedades.
- Si $\lambda, \mu \in\mathbb{C}$ son dos constantes, entonces:
\begin{equation*}
\int_{\gamma} \left[\lambda f(z) + \beta g(z)\right] dz = \lambda \int_{\gamma} f(z) dz + \beta \int_{\gamma} g(z) dz.
\end{equation*} - \begin{equation*}
\int_{-\gamma} f(z) dz = – \int_{\gamma} f(z) dz.
\end{equation*} - Si el contorno $\gamma$ es tal que $\gamma = \gamma_1 + \gamma_2$, entonces:
\begin{equation*}
\int_{\gamma} f(z) dz = \int_{\gamma_1} f(z) dz + \int_{\gamma_2} f(z) dz.
\end{equation*}En general, si $\gamma = \gamma_1 + \cdots + \gamma_n$, entonces:
\begin{equation*}
\int_{\gamma} f(z) dz = \int_{\gamma_1} f(z) dz + \cdots + \int_{\gamma_n} f(z) dz = \sum_{k=1}^n \int_{\gamma_k} f(z) dz.
\end{equation*}
Demostración. Dadas las hipótesis.
- Se deja como ejercicio al lector.
- De acuerdo con la definición 32.12 sabemos que $-\gamma(t) = \gamma(b+a-t)$ para toda $t\in[a,b]$, entonces, para $s=b+a-t$, por la observación 34.2, la definición 34.1, el teorema 34.1, la regla de la cadena y la proposición 33.1(7), tenemos que:
\begin{align*}
\int_{-\gamma} f(z) dz & = \int_{a}^{b} f(-\gamma(t)) \left[-\gamma(t)\right]’dt\\
& = \int_{a}^{b} f(\gamma(a+b-t)) \left[-\gamma'(a+b-t)\right]dt\\
& = \int_{b}^{a} f(\gamma(s)) \gamma'(s)ds\\
& = -\int_{a}^{b} f(\gamma(s)) \gamma'(s)ds\\
& = – \int_{\gamma} f(z) dz.
\end{align*} - Supongamos que existen $\gamma_1:[a_1, b_1] \to U$ y $\gamma_2:[a_2, b_2] \to U$ tales que $a=a_1$, $b=b_1+b_2-a_2$ y $\gamma_1(b_1)=\gamma_2(a_2)$, es decir, $\gamma=\gamma_1+\gamma_2$, entonces, por las definiciones 32.13, 34.1, la observación 34.2, la proposición 33.1(4) y el teorema 34.1, para $s=t-b_1+a_2$ tenemos que:
\begin{align*}
\int_{\gamma} f(z) dz & = \int_{\gamma_1+\gamma_2} f(z) dz\\
& = \int_{a}^{b_1+b_2-a_2} f\left[\left(\gamma_1+\gamma_2\right)(t)\right] \left(\gamma_1+\gamma_2\right)'(t)dt\\
& = \int_{a}^{b_1} f(\gamma_1(t)) \gamma_1′(t)dt + \int_{b_1}^{b_1+b_2-a_2} f(\gamma_2(t-b_1+a_2)) \gamma_2′(t-b_1+a_2)dt\\
& = \int_{a}^{b_1} f(\gamma_1(t)) \gamma_1′(t)dt + \int_{a_2}^{b_2} f(\gamma_2(s)) \gamma_2′(s)ds\\
& = \int_{\gamma_1} f(z) dz + \int_{\gamma_2} f(z) dz.
\end{align*}El caso general se deja como ejercicio al lector.
$\blacksquare$
Observación 34.4.
Notemos que si $\gamma:[0,1] \to \mathbb{C}$ está dada por $\gamma(t)=it$ y $f(z)=1$, tenemos que:
\begin{align*}
\int_{\gamma} f(z) dz & = \int_{0}^{1} f(\gamma(t)) \gamma'(t)dt\\
& = \int_{0}^{1} 1 \cdot i \, dt\\
& = i.
\end{align*}
De donde se sigue que $\operatorname{Re}\left(\displaystyle \int_{\gamma} f(z) dz \right) = 0$.
Sin embargo, tenemos que $\operatorname{Re} f(z) = 1$, por lo que:
\begin{equation*}
\int_{\gamma} \operatorname{Re} f(z) dz = i.
\end{equation*}
Entonces, a diferencia de las integrales de funciones híbridas, para las integrales de contorno, en general tenemos que:
\begin{equation*}
\operatorname{Re}\left(\displaystyle \int_{\gamma} f(z) dz \right) \neq \int_{\gamma} \operatorname{Re} f(z) dz.
\end{equation*}
Ejemplo 34.6.
Verifiquemos el resultado del ejemplo 34.4 utilizando la proposición 34.2(3).
Solución. Para todo $t\in [0,1]$ se cumple que:
\begin{align*}
[0,1+i](t) & = (1+i)t, \quad [0,1+i]'(t) = 1+i,\\
[1+i,i](t) & = 1+i -t, \quad [1+i,i]'(t) = -1.
\end{align*}
Entonces, de acuerdo con la definición 34.1 y las proposiciones 33.2 y 34.2(3), tenemos que:
\begin{align*}
\int_{\gamma} (x+y) dz & = \int_{[0,1+i]} (x+y) dz + \int_{[1+i,i]} (x+y) dz\\
& = \int_{0}^{1} 2t(1+i) dt + \int_{0}^{1} (2-t)(-1) dt\\
&= \left.(1+i)t^2\right|_{0}^{1} + \left.\left[\frac{t^2}{2} – 2t\right]\right|_{0}^{1}\\
& = -\frac{1}{2} + i.
\end{align*}
Observación 34.5.
Aunque puede suceder que la integral de contorno de una función compleja a lo largo de dos curvas distintas sea la misma, esto en general no es cierto.
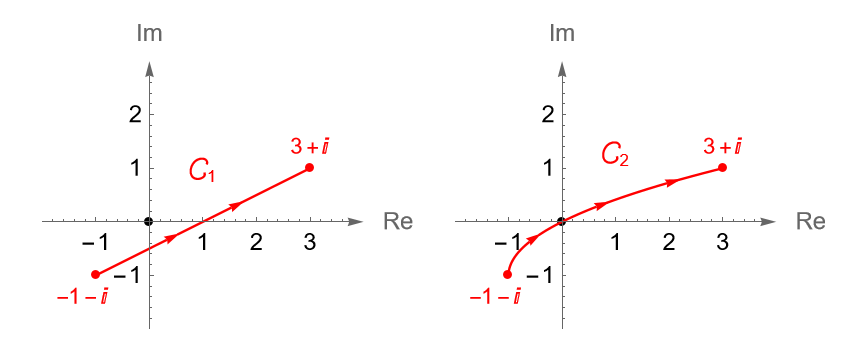
Ejemplo 34.7.
Veamos que:
\begin{equation*}
\int_{C_1} z dz = \int_{C_2} z dz,
\end{equation*}donde $C_1$ es el contorno dado por el segmento de recta que une a $z_1 = -1-i$ con $z_2 = 3+i$ y $C_2$ es el contorno que va de $z_1$ a $z_2$ a través del pedazo de la parábola $x=y^2+2y$, figura 123.
Solución. De acuerdo con el ejemplo 32.2, podemos parametrizar al contorno $C_1$ mediante la trayectoria $\gamma_1:[0,1]\to\mathbb{C}$ dada por:
\begin{equation*}
\gamma_1(t) = -1-i+[3+i-(-1-i)]t = -1-i+(4+2i)t, \quad \forall t\in[0,1].
\end{equation*}
Por otra parte, podemos parametrizar al contorno $C_2$ como $\gamma_2(t)=x_2(t)+iy_2(t)$, donde:
\begin{equation*}
x_2(t)=t^2+2t, \quad y_2(t)=t.
\end{equation*}
Tenemos que $ t\in\mathbb{R}$, por lo que si $\gamma_2(t)=-1-i$, entonces:
\begin{equation*}
t^2+t(2+i)+1+i = (t+1)(t+1+i)=0 \quad \Longrightarrow \quad t=-1.
\end{equation*}
Análogamente, si $\gamma_2(t)=3+i$, entonces:
\begin{equation*}
t^2+t(2+i)-3-i = (t-1)(t+3+i)=0 \quad \Longrightarrow \quad t=1.
\end{equation*}
Por lo tanto $\gamma_2 : [-1,1]\to \mathbb{C}$, dada por $\gamma_2(t)=t^2+2t+it$, es una parametrización de $C_2$.
De acuerdo con la definición 34.1 y las proposiciones 33.1 y 33.2, tenemos que:
\begin{align*}
\int_{C_1} z dz & = \int_{0}^{1} \left[-1-i+(4+2i)t\right](4+2i) dt\\
& = (-1-i)(4+2i) \int_{0}^{1} dt + (4+2i)^2 \int_{0}^{1} t dt\\
& = (-2-6i) \left. t\right|_{0}^{1} + 4(3+4i) \left. \frac{t^2}{2}\right|_{0}^{1}\\
& = -2-6i + 6+8i\\
& = 4+2i.
\end{align*}
\begin{align*}
\int_{C_2} z dz & = \int_{-1}^{1} \left[t^2+2t+it\right](2t+2+i)dt\\
& = \int_{-1}^{1} \left[2t^3+6t^2+3t+i(3t^2+4t)\right]dt\\
& = \int_{-1}^{1} \left(2t^3+6t^2+3t\right)dt + +i\int_{-1}^{1}\left(3t^2+4t\right) dt\\
& = \left. \left(\frac{t^4}{2}+2t^3+\frac{3t^2}{2}\right)\right|_{-1}^{1} + \left. i\left(t^3+2t^2\right)\right|_{-1}^{1}\\
& = 4+2i.
\end{align*}
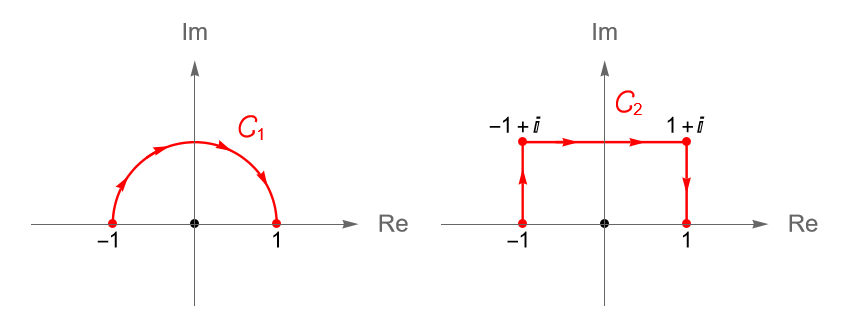
Ejemplo 34.8.
Veamos que:
\begin{equation*}
\int_{C_1} \overline{z} dz = -\pi i \quad \text{y} \quad \int_{C_2} \overline{z} dz = -4i,
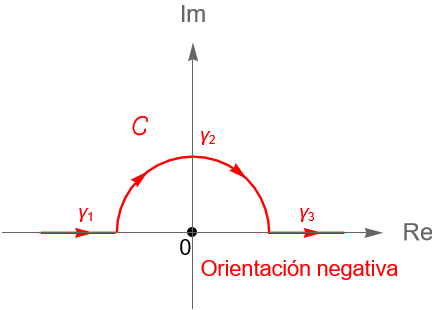
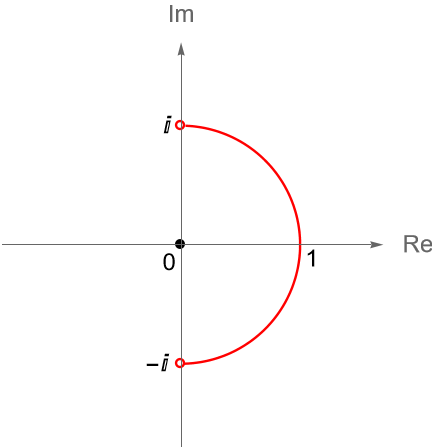
\end{equation*}donde $C_1$ es el contorno que va de $-1$ a $1$ a través de la semicircunferencia unitaria superior y $C_2$ es el contorno que va de $-1$ a $1$ a través de la poligonal $[z_1, z_2, z_3, z_4]$, donde $z_1 = -1, z_2 = -1+i, z_3=1+i$ y $z_4 = 1$, ambos orientados negativamente, figura 124.
Solución. Considerando la definición 32.12, podemos parametrizar a $C_1$ mediante la curva opuesta de la semicircunferencia unitaria superior, orientada positivamente, es decir, $\beta(t)=e^{it}$, con $0\leq t \leq \pi$. Entonces, una parametrización del contorno $C_1$ está dada por la trayectoria $\gamma_1:[0,\pi]\to\mathbb{C}$ dada por:
\begin{equation*}
\gamma_1(t):= -\beta(t) = \beta(\pi + 0 – t) = \beta(\pi-t) = e^{i(\pi-t)} = -e^{-it}, \quad \forall t\in[0,\pi].
\end{equation*}
Considerando lo anterior, del ejemplo 32.1 se sigue que:
\begin{equation*}
\gamma_1′(t) = \frac{d}{dt} \left(-e^{-it}\right) = -(-i)e^{-it} = ie^{-it}.
\end{equation*}
Por otra parte, de acuerdo con la definición 32.13 y la observación 32.15, podemos parametrizar al contorno $C_2$, descrito por la poligonal $[z_1, z_2, z_3, z_4]$, donde $z_1 = -1, z_2 = -1+i, z_3=1+i$ y $z_4 = 1$, a través de la trayectoria $\gamma_2=[z_1, z_2] + [z_2, z_3] + [z_3, z_4]$. De acuerdo con el ejemplo 32.2 tenemos que:
\begin{align*}
[z_1, z_2](t) & = -1 + [-1+i-(-1)]t = -1+it,\\
[z_2, z_3](t) & = -1+i + [1+i-(-1+i)]t = -1+2t+i,\\
[z_3, z_4](t) & = 1+i + [1-(1+i)]t = 1+i(1-t),
\end{align*}donde $t\in[0,1]$ para los tres segmentos de recta. Entonces:
\begin{align*}
[z_1, z_2]'(t) & = \frac{d}{dt} \left(-1+it\right) = i,\\
[z_2, z_3]'(t) & = \frac{d}{dt} \left(-1+2t+i\right) = 2,\\
[z_3, z_4]'(t) & = \frac{d}{dt} \left(1+i(1-t)\right) = -i.
\end{align*}
Utilizando la definición 32.13 es fácil obtener de manera explícita la regla de correspondencia de $\gamma_2$, sin embargo, podemos utilizar la proposición 34.2(3) y simplificar las cuentas.
Por lo tanto, de la definición 34.1 y las proposiciones 20.2 y 33.1, tenemos que:
\begin{align*}
\int_{C_1} \overline{z} dz & = \int_{0}^{\pi} \overline{-e^{-it}}(ie^{-it}) dt\\
& = -i\int_{0}^{\pi}e^{it}e^{-it} dt\\
& = -i\int_{0}^{\pi} e^{0} dt\\
& = -i \pi.
\end{align*}
Mientras que de la definición 34.1 y las proposiciones 34.2(3), 33.1 y 33.2, se sigue que:
\begin{align*}
\int_{C_2} \overline{z} dz & = \int_{ [z_1, z_2]} \overline{z} dz + \int_{ [z_2, z_3]} \overline{z} dz + \int_{ [z_3, z_4]} \overline{z} dz\\
& = \int_{0}^{1} \left(\overline{-1+it}\right) i dt + \int_{0}^{1} \left(\overline{-1+2t+i}\right) 2 dt + \int_{0}^{1} \left[\overline{1+i(1-t)}\right](-i) dt\\
& = i\int_{0}^{1} \left(-1-it\right) dt + 2 \int_{0}^{1} \left(-1+2t-i\right) dt -i \int_{0}^{1} \left[1-i(1-t)\right] dt\\
& = \left.i\left(-t-i\frac{t^2}{2}\right)\right|_{0}^{1} + \left. 2 \left(-t+t^2-it\right)\right|_{0}^{1} – \left. i \left[t+i\frac{(1-t)^2}{2}\right]\right|_{0}^{1}\\
& = i\left(-1-\frac{i}{2}\right) – 2i – i \left(1-\frac{i}{2}\right)\\
& = -4i.
\end{align*}
Definición 34.2. (Integral con respecto de la longitud de arco.)
Sean $U\subset\mathbb{C}$ un conjunto abierto, $[a,b]\subset\mathbb{R}$, con $a<b$ un intervalo cerrado, $f: U \to \mathbb{C}$ una función continua en $U$ y $\gamma:[a,b] \to U$ un contorno en $U$. Se define a la integral de $f$ {\bf con respecto de la longitud de arco $|dz|$}, a lo largo de $\gamma$, como:
\begin{equation*}
\int_{\gamma} f(z) |dz| := \int_{a}^{b} f(\gamma(t)) \left|\gamma'(t)\right| dt.\tag{34.3}
\end{equation*}
Si el contorno está dado por una trayectoria $\gamma$ suave a trozos, para la partición:
\begin{equation*}
P : a=t_0 < t_1 < \cdots < t_{n-1}<t_n=b,
\end{equation*}del intervalo $[a,b]$, tal que $\gamma_k$, la restricción de $\gamma$ al intervalo $[t_{k-1}, t_k]$, es una curva suave para $1\leq k\leq n$, se cumple que:
\begin{equation*}
\int_{\gamma} f(z) |dz| = \int_{\gamma_1} f(z) |dz| + \cdots + \int_{\gamma_n} f(z) |dz| = \sum_{k=1}^n \int_{\gamma_k} f(z) |dz|. \tag{34.4}
\end{equation*}
Observación 34.6.
Notemos que si $f(z)=1$, entonces de (34.3) obtenemos:
\begin{equation*}
\int_{\gamma}|dz| = \int_{a}^{b} \left|\gamma'(t)\right| dt,
\end{equation*}la cual corresponde con la longitud de arco de una curva en $\mathbb{C}$, definición 32.15.
El siguiente resultado justifica la definición anterior.
Lema 34.1.
Si $\gamma$ es una curva suave a trozos, es decir, un contorno en $\mathbb{C}$, entonces $\gamma$ es rectificable (definición 32.16) y la longitud de arco de dicha curva es:
\begin{equation*}
\ell(\gamma)=\int_{\gamma}|dz|.
\end{equation*}
Se puede consultar una prueba detallada de este resultado en:
- An Introduction to Complex Function Theory, Bruce P. Palka.
- Function of One Complex Variable, John B. Conway.
- Teoría de funciones de una variable compleja, Felipe Zaldívar.
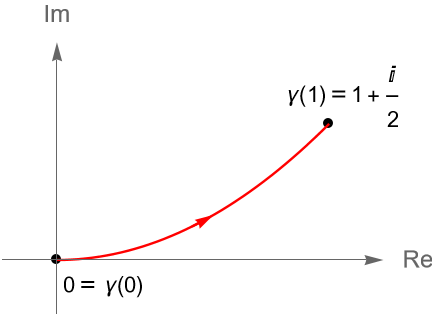
Ejemplo 34.9.
Evaluemos las siguientes integrales.
a) $\displaystyle \int_{\gamma} z^{-2} |dz|$, donde la trayectoria $\gamma$ describe a la circunferencia $C(0,2)$ orientada positivamente, es decir, $\gamma(t)=2e^{it}$, con $0\leq t\leq 2\pi$.
b) $\displaystyle \int_{\gamma} x |dz|$, donde $\gamma(t)=t+i\left(\dfrac{t^2}{2}\right)$, con $0\leq t\leq 1$, figura 125.
Solución.
a) Es claro que $\gamma$ es un contorno y $\gamma'(t)=i2e^{it}$. Más aún, sabemos que la función $f(z)=z^{-2}$ es analítica en el dominio $D=\mathbb{C}\setminus\{0\}$, por lo que es continua en $D$ y el contorno descrito por $\gamma$ está completamente contenido en $D$. Entonces, por la definción 34.2, las proposiciones 20.2(6), 20.2(7), 33.1(3) y el ejemplo 33.2, tenemos que:
\begin{align*}
\int_{\gamma} z^{-2} |dz| & = \int_{0}^{2\pi} \left(2e^{it}\right)^{-2}\left|i2e^{it}\right| dt\\
& = \frac{1}{2} \int_{0}^{2\pi}e^{-i2t} dt\\
& = \frac{1}{2}(0)\\
& = 0.
\end{align*}
b) Es claro que $\gamma$ es un contorno, con $\gamma'(t)=1+it$. Por otra parte, por el ejemplo 15.1(a) sabemos que la función $f(z)=\operatorname{Re}(z)=x$, para $z=x+iy\in\mathbb{C}$, es continua en todo $\mathbb{C}$. Entonces, por la definción 34.2 tenemos que:
\begin{align*}
\int_{\gamma} x |dz| & = \int_{0}^{1} t\left|1+t^2\right| dt\\
& = \frac{1}{2} \int_{0}^{1}2t\sqrt{1+t^2}dt\\
& = \frac{1}{2} \left.\left[ \frac{2\left(1+t^2\right)^{3/2}}{3}\right]\right|_{0}^{1}\\
& = \frac{2\sqrt{2}-1}{3}.
\end{align*}
Proposición 34.3. (Propiedades integrales con respecto de la longitud de arco.)
Sean $U\subset\mathbb{C}$ un conjunto abierto, $[a,b]\subset\mathbb{R}$, con $a<b$ un intervalo cerrado, $f, g: U \to \mathbb{C}$ dos funciones continuas en $U$ y $\gamma:[a,b] \to U$ un contorno en $U$. Se cumplen las siguientes propiedades.
- Si $\lambda, \mu \in\mathbb{C}$ son dos constantes, entonces:
\begin{equation*}
\int_{\gamma} \left[\lambda f(z) + \beta g(z)\right] |dz| = \lambda \int_{\gamma} f(z) |dz| + \beta \int_{\gamma} g(z) |dz|.
\end{equation*} - \begin{equation*}
\int_{-\gamma} f(z) |dz| = \int_{\gamma} f(z) |dz|.
\end{equation*} - Si el contorno $\gamma$ es tal que $\gamma = \gamma_1 + \gamma_2$, entonces:
\begin{equation*}
\int_{\gamma} f(z) |dz| = \int_{\gamma_1} f(z) |dz| + \int_{\gamma_2} f(z) |dz|.
\end{equation*}En general, si $\gamma = \gamma_1 + \cdots + \gamma_n$, entonces:
\begin{equation*}
\int_{\gamma} f(z) |dz| = \int_{\gamma_1} f(z) |dz| + \cdots + \int_{\gamma_n} f(z) |dz| = \sum_{k=1}^n \int_{\gamma_k} f(z) |dz|.
\end{equation*} - Si $\beta$ es una reparametrización de $\gamma$, entonces:
\begin{equation*}
\int_{\beta} f(z) |dz| = \int_{\gamma} f(z) |dz|.
\end{equation*} - \begin{equation*}
\left|\int_{\gamma} f(z) dz \right| \leq \int_{\gamma} |f(z)| |dz|.
\end{equation*}En particular, si $M$ es una constante tal que $|f(z)|\leq M$ y $L=\ell\left(\gamma\right)$, entonces:
\begin{equation*}
\left|\int_{\gamma} f(z) dz\right| \leq ML.
\end{equation*}
Demostración. Dadas las hipótesis.
- Se deja como ejercicio al lector.
- Se deja como ejercicio al lector.
- Se deja como ejercicio al lector.
- Se deja como ejercicio al lector.
- De acuerdo con la definición 34.1 y la proposición 33.1(5) tenemos que:
\begin{align*}
\left|\int_{\gamma} f(z) dz \right| & = \left| \int_{a}^{b} f(\gamma(t)) \gamma'(t) dt\right|\\
& \leq \int_{a}^{b} \left| f(\gamma(t))\gamma'(t)\right| dt\\
& = \int_{a}^{b} \left| f(\gamma(t))\right| \, \left|\gamma'(t)\right| dt\\
& = \int_{\gamma} |f(z)| |dz|.
\end{align*}Si $M=\max\limits_{z\in\gamma}|f(z)|$ y $L=\ell\left(\gamma\right)$, entonces $|f(z)| \leq M$, por lo que de la monotonía de la integral para funciones reales se sigue que:
\begin{equation*}
\left|\int_{\gamma} f(z) dz \right| \leq \int_{\gamma} |f(z)| |dz| \leq \int_{a}^{b} M |\gamma'(t)| dt = ML.
\end{equation*}
$\blacksquare$
Observación 34.7.
Muchas veces, en la teoría y en la práctica, no es necesario evaluar una integral de contorno, sino que simplemente basta con obtener una cota superior de su módulo, por ello la propiedad dada en la proposición 34.3(5) es de mucha utilidad.
Ejemplo 34.10.
Determinemos una cota superior para:
\begin{equation*}
\left|\int_{\gamma} \frac{e^{z}}{z^2+1} dz \right|,
\end{equation*}donde $\gamma$ describe a la circunferencia $C(0,2)$ en sentido positivo.
Solución. Tenemos que una parametrización del contorno $C(0,2)$ es $\gamma(t)=2e^{it}$, para $0\leq t \leq 2\pi$. Sabemos que $\gamma'(2)=i2e^{it}$, entonces, de la proposición 20.2(6) y la definción 32.15 se sigue que:
\begin{equation*}
L := \ell(\gamma) = \int_{0}^{2\pi}|\gamma'(t)| dt = \int_{0}^{2\pi}|i2e^{it}| dt = \int_{0}^{2\pi} 2 dt = 4\pi.
\end{equation*}
Por el corolario 16.1(2) es claro que la función racional:
\begin{equation*}
f(z) = \frac{e^{z}}{z^2+1},
\end{equation*}es analítica en $D=\mathbb{C}\setminus\{-i, i\}$ y por tanto continua en $D$. Además el contorno $C(0,2)$ está completamente contenido en $D$.
Por la proposición 20.2(4), para $z=x+iy\in\mathbb{C}$ sabemos que $|e^z| = e^x$ y de la observación 3.1 tenemos que $x = \operatorname{Re}(z)\leq |z|$, entonces, corolario 31.1(1), $|e^z| \leq e^{|z|}$.
De lo anterior, para $z=\gamma(t)$ tenemos que:
\begin{equation*}
\left|e^{2e^{it}}\right| \leq e^{|2e^{it}|} = e^{2},
\end{equation*}y considerando la desigualdad del triángulo, proposición 3.3, tenemos que:
\begin{equation*}
\left|z^2+1\right| = \left|\left(2e^{it}\right)^2+1\right| = \left|4e^{i2t}+1\right| \geq \left|4e^{i2t}\right| – \left|1\right| = 4-1=3.
\end{equation*}
Entonces, para $z=\gamma(t)$, es decir, para $|z|=2$, se cumple que:
\begin{equation*}
\left|f(z)\right| = \left|\frac{e^{z}}{z^2+1}\right| \leq \frac{e^2}{3} =: M.
\end{equation*}
Por lo tanto, por la proposición 34.3(5) tenemos que:
\begin{equation*}
\left|\int_{\gamma} \frac{e^{z}}{z^2+1} dz \right| \leq M L = \frac{4\pi e^2}{3}.
\end{equation*}
Ejemplo 34.11.
Sea $r>0$. Veamos que:
\begin{equation*}
\left|\int_{\gamma} e^{iz^2} dz \right| \leq \frac{\pi(1-e^{-r^2})}{4r},
\end{equation*}donde $\gamma(t) = re^{it}$, con $0\leq t \leq \dfrac{\pi}{4}$.
Solución. Sabemos que la función $f(z)=e^{iz^2}$ es entera y por tanto continua en $\mathbb{C}$. Por otra parte, es claro que el arco de circunferencia $C(0,r)$ descrito por $\gamma(t) = re^{it}$, $0\leq t \leq \dfrac{\pi}{4}$, es un contorno en $\mathbb{C}$ y $\gamma'(t)=ire^{it}$. Entonces, por la proposición 20.2(6), es claro que:
\begin{equation*}
\left|\gamma'(t)\right| = \left|ire^{it}\right| = r.
\end{equation*}
Si $z=x+iy\in\mathbb{C}$, entonces $iz^2= i(x^2-y^2) – 2xy$, por lo que, de acuerdo con la proposición 20.2(4), tenemos que:
\begin{equation*}
\left|f(z)\right| = \left|e^{iz^2}\right| = e^{\operatorname{Re}\left(iz^2\right)} = e^{-2xy}.
\end{equation*}
De la proposición 20.2(5) se sigue que $\gamma(t)=re^{it} = r\operatorname{cos}(t)+ir\operatorname{cos}(t)$, entonces:
\begin{equation*}
\left|f\left(\gamma(t)\right)\right| = e^{-2r^2\operatorname{cos}(t)\operatorname{sen}(t)} = e^{-r^2\operatorname{sen}(2t)}.
\end{equation*}
Sea $u=2t$. Notemos que:
\begin{equation*}
0\leq u \leq \dfrac{\pi}{2} \quad \Longrightarrow \quad \operatorname{sen}(u) \geq \frac{2u}{\pi} \quad \Longrightarrow \quad -r^2 \operatorname{sen}(u) \leq -\frac{2ur^2}{\pi}.
\end{equation*}
Por lo que:
\begin{align*}
\int_{\gamma} \left|f(z)\right| |dz| & = \int_{0}^{\pi/4} \left|f\left(\gamma(t)\right)\right| \, \left|\gamma'(t)\right| dt\\
& = \int_{0}^{\pi/4} r e^{-r^2\operatorname{sen}(2t)} dt\\
& = \frac{r}{2} \int_{0}^{\pi/2} e^{-r^2\operatorname{sen}(u)} du\\
& \leq \frac{r}{2} \int_{0}^{\pi/2} \operatorname{exp}\left(-\dfrac{2ur^2}{\pi}\right) du\\
& = \left.\left[-\dfrac{\pi \operatorname{exp}\left(-\dfrac{u2r^2}{\pi}\right)}{4r}\right]\right|_{0}^{\pi/2}\\
& = \frac{\pi(1-e^{-r^2})}{4r}.
\end{align*}
Entonces, por la proposición 34.3(5) tenemos que:
\begin{equation*}
\left|\int_{\gamma} e^{iz^2} dz \right| \leq \int_{\gamma} \left|e^{iz^2}\right| \, |dz| \leq \frac{\pi(1-e^{-r^2})}{4r}.
\end{equation*}
Observación 34.8.
En este punto es importante hacer un comentario sobre la notación para integrales de contorno a lo largo de segmentos de recta. Si $f$ es una función compleja continua en el segmento de recta que une a los puntos $z_1, z_2\in\mathbb{C}$, con $z_1\neq z_2$, es decir, $f$ es continua en $[z_1, z_2]$, entonces denotamos lo anterior como:
\begin{equation*}
\int_{[z_1, z_2]} f(z) dz := \int_{z_1}^{z_2} f(z) dz.
\end{equation*}
\begin{equation*}
\int_{[z_1, z_2]} f(z) |dz| := \int_{z_1}^{z_2} f(z) |dz|.
\end{equation*}
Así por ejemplo, como $[z_2, z_1](t) = -[z_1, z_2](t)$, de la proposición 34.2(2) se sigue que:
\begin{equation*}
\int_{z_2}^{z_1} f(z) dz = – \int_{z_1}^{z_2} f(z) dz.
\end{equation*}
Además, como $[z_1, z_1]$ corresponde con un contorno constante, entonces:
\begin{equation*}
\int_{z_1}^{z_1} f(z) dz = 0.
\end{equation*}
Considerando lo anterior, si $z_3$ es un tercer punto en el segmento $[z_1, z_2]$, distinto de $z_1$ y de $z_2$, entonces:
\begin{equation*}
\int_{z_1}^{z_2} f(z) dz = \int_{z_1}^{z_3} f(z) dz + \int_{z_3}^{z_2} f(z) dz.
\end{equation*}
Debe ser claro que lo anterior no es una consecuencia directa de la proposición 34.2(3), ya que si consideramos la definición 32.13, no es difícil verificar que el contorno dado por $[z_1, z_3] + [z_3, z_2]$ no es igual al contorno dado por $[z_1, z_2]$.
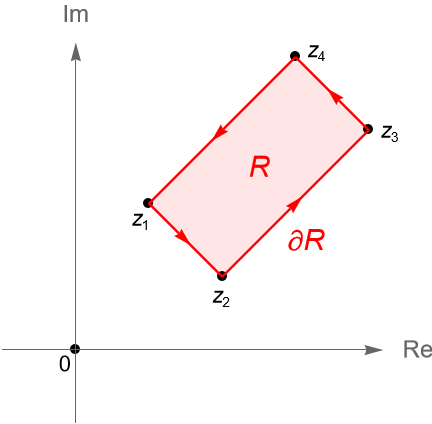
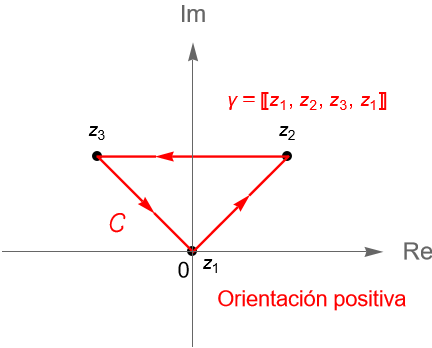
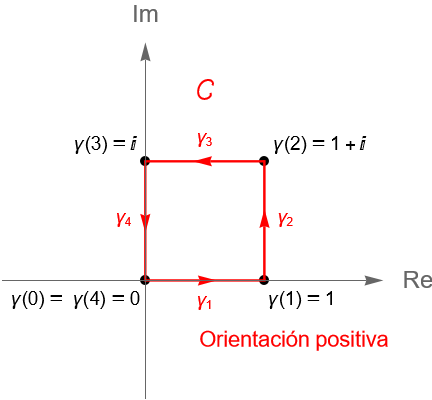
Ejemplo 34.12.
Si $R\subset\mathbb{C}$ es un rectángulo en el plano complejo con vértices $z_1, z_2, z_3, z_4\in\mathbb{C}$, entonces el contorno poligonal dado por $\gamma = [z_1, z_2] + [z_2, z_3] + [z_3, z_4] + [z_4, z_1]$ parametriza a la frontera $\partial R$ de dicho rectángulo, en sentido positivo relativo a $R$, figura 126. Considerando la notación dada en la observación 34.6, la integral de contorno de una función $f$ continua a lo largo de $\gamma$ está dada por:
\begin{equation*}
\int_{\delta R} f(z) dz = \int_{z_1}^{z_2} f(z) dz + \int_{z_2}^{z_3} f(z) dz + \int_{z_3}^{z_4} f(z) dz + \int_{z_4}^{z_1} f(z) dz.
\end{equation*}
Tarea moral
- Completa las demostraciones de las proposiciones 34.2 y 34.3.
- Evalúa las siguientes integrales.
a) $\displaystyle \int_{\gamma} (2xy-ix^2) dz$, donde $\gamma(t)=t+it^2$, con $0\leq t\leq 1$.
b) $\displaystyle \int_{\gamma} \dfrac{z^2-1}{z(z^2+4)} dz$, donde $\gamma(t)=e^{it}$, con $0\leq t\leq 2\pi$.
Hint: Utiliza fracciones parciales.
c) $\displaystyle \int_{C} z^2 |dz|$, donde $C=C(i,2)$, orientada positivamente.
d) $\displaystyle \int_{\gamma} z |dz|$, donde $C\gamma=[e, 1] + [1, -1+i\sqrt{3}]$. - Sea $C$ el contorno dado por el segmento de recta que va de $1$ a $i$. Determina una cota superior para:
\begin{equation*}
\left|\int_{C} \operatorname{cos}^2(z) dz\right|.
\end{equation*} - Sea $f:C(0,1) \to \mathbb{C}$ una función continua tal que $|f(z)|\leq M$ para todo $z\in C(0,1)$, con $M>0$. Prueba que si:
\begin{equation*}
\left|\int_{C(0,1)} f(z) dz\right| = 2\pi M,
\end{equation*}
entonces $f(z)=c\overline{z}$, donde $c\in\mathbb{C}$ es una constante tal que $|c|=M$.
Hint: Considera el ejercicio 4 de la entrada 33. - Si $\gamma(t)=e^{1+it}$, con $0\leq t \leq \pi$, muestra que:
\begin{equation*}
\left|\int_{\gamma} \left[\operatorname{Log}(z)\right]^{-1} dz\right| \leq e \operatorname{Log}(\pi+\sqrt{\pi^2+1}).
\end{equation*} - Sean $P(z)$ y $Q(z)$ dos polinomios complejos de grado $n$ y $m$, respectivamente, tales que $m\geq n+2$. Muestra que:
\begin{equation*}
\lim\limits_{r\to \infty} \int_{C} \frac{P(z)}{Q(z)} dz = 0,
\end{equation*}donde el contorno $C$ es la circunferencia $C(0,r)$.
Hint: Utiliza la proposición 34.3(5). - Evalúa la integral $\int_{\gamma} \overline{z} dz$, donde:
a) $\gamma$ es el pedazo de la parábola $y=x^2$ que va de $0$ a $1+i$;
b) $\gamma$ es el arco de la cicloide dada por:
\begin{equation*}
x(t)=a(t-\operatorname{sen}(t)), \quad y(t)=a(1-\operatorname{cos}(t)),
\end{equation*}entre los puntos $(0,0)$ y $(a\pi, 2a)$, con $a>0$. - Verifica que:
\begin{equation*}
\int_{\gamma_1} \frac{1}{z} dz \neq \int_{\gamma_2} \frac{1}{z} dz,
\end{equation*}donde $\gamma_1(t)=e^{-it}$ y $\gamma_2(t)=e^{it}$, con $t\in[0,2\pi]$.
Más adelante…
En esta entrada hemos definido de manera formal lo que es una integral de una función compleja de variable compleja. Como vimos, esta definición es similar a la de una integral de línea y muchos de las propiedades de este tipo de integrales están sustentados por la teoría de integración para integrales reales, por lo que la operabilidad de estas integrales resulta sencilla gracias a los resultados de nuestros cursos de Cálculo.
En la siguiente entrada probaremos el Teorema Fundamental del Cálculo para integrales de contorno y el lema de Goursat, así como otros resultados importantes sobre las integrales de contorno para funciones complejas, los cuales nos serán de utilidad para probar algunos de los resultados fundamentales en la teoría de la Variable Compleja, como el teorema de Cauchy.
Entradas relacionadas
- Ir a Variable Compleja I.
- Entrada anterior del curso: Integrales de funciones híbridas.
- Siguiente entrada del curso: Integrales de contorno II.