Introducción
Para esta unidad veremos diferentes aplicaciones de la integral en algunas diferentes ramas en donde son de utilidad las integrales para calcular algún objetivo en concreto.
En la unidad anterior vimos las técnicas de integración para resolver integrales, ahora que ya sabemos unas cuantas técnicas que nos permitirá facilitar los temas que vienen por delante. En esta sección veremos como calcular el área entre curvas, es decir, determinar el área entre dos gráficas acotadas por dos funciones.
Área entre curvas
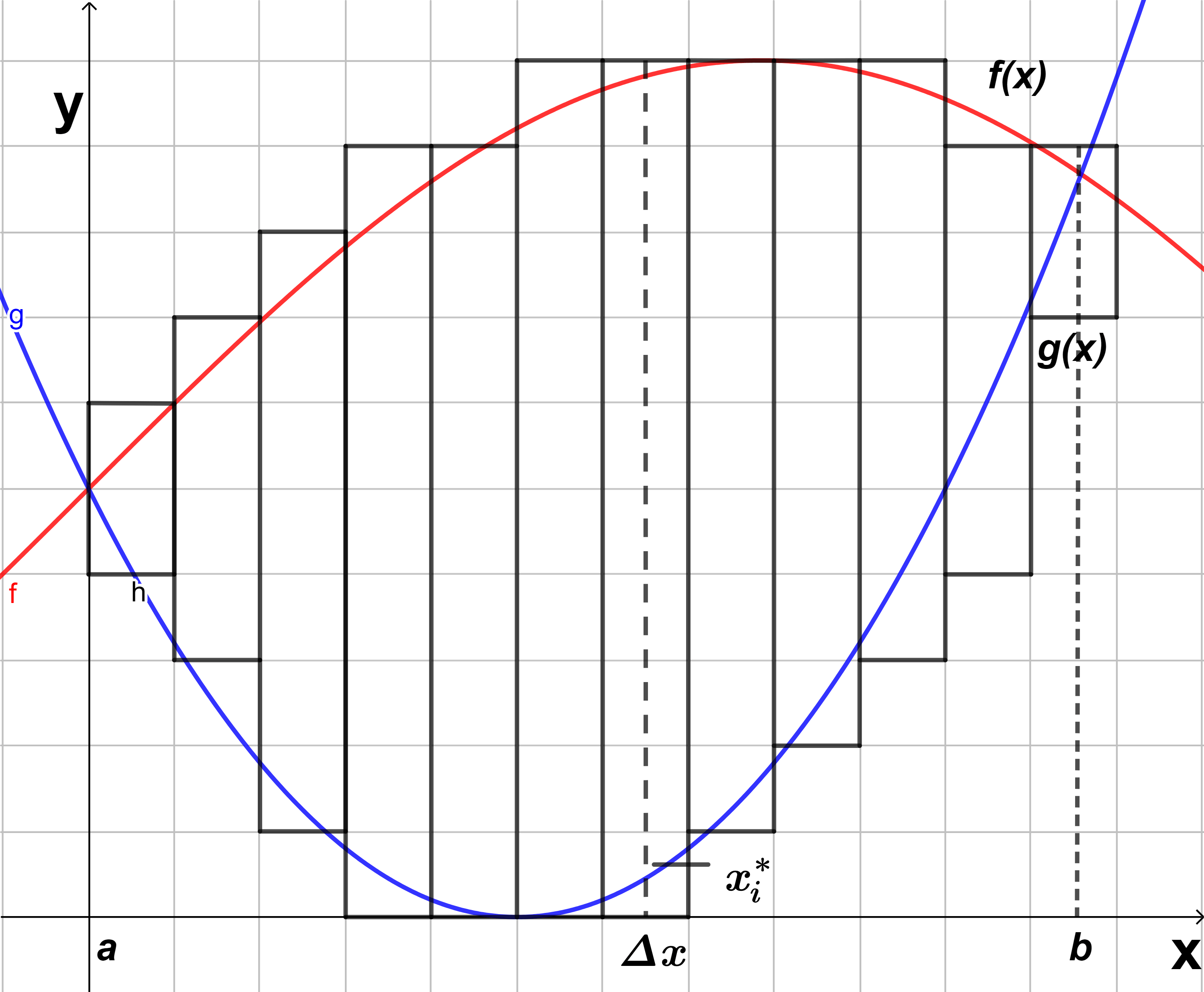
Queremos encontrar el área que está acotada por una curva $y=f(x)$ y $y=g(x)$ entre las rectas verticales $x=a$ y $x=b$ como se muestra en la figura $(1)$, donde $f$ y $g$ son funciones continuas en el intervalo $[a,b]$, supóngase que $f(x) \geq g(x)$, para encontrar esa área, aproximamos la región con $n$ rectángulos basándonos en una partición $P=\left \{ x_{0}, x_{1},…, x_{n} \right \}$ en $[a, b]$ como se ve en la figura $(1)$, donde el área del k-ésimo rectángulo con base $\Delta x$ y altura $f(x_{i}^{*})-g(x_{i}^{*})$ es:
$$A=(f(x_{i}^{*})-g(x_{i}^{*}))\Delta x$$
Por tanto, sumando las áreas de todos los $n$ rectángulos aproximando al área entre las gráficas, obtenemos:
$$\sum_{i=1}^{n}(f(x_{i}^{*})-g(x_{i}^{*}))\Delta x$$
Tendremos una mejor aproximación si $n \rightarrow \infty$. Por tanto, definimos el área $A$ de $S$ como el valor límite de la suma de las áreas de los rectángulos de aproximación como:
$$A=\lim_{n \rightarrow \infty }\sum_{i=1}^{n}(f(x_{i}^{*})-g(x_{i}^{*}))\Delta x$$
Vemos que esta suma es una suma de Riemann [Hipervinculo: Calculo II. Definicion de la integral ],por lo que definimos el área entre curvas como sigue.
Definición. Si $f$ y $g$ son continuas con $f(x) \geq g(x)$ en todo $[a, b]$, el área de la región entre las curvas $y=f(x)$ y $y=g(x)$ y las rectas $x=a$ y $x=b$, está dada por la integral:
$$A=\int_{a}^{b}[f(x)-g(x)]dx$$
Por lo que al área que está acotada entre dos funciones lo podemos calcular por medio de una integral, veamos unos ejemplos.
Ejemplos
- Determine el área de la región acotada entre las curvas $y=e^{x}$, $y=x$ y las rectas $x=0$ y $x=1$
Graficamos las curvas como se muestra en la figura $(2)$, vemos que $e^{x} > x$ en todo el intervalo $[0, 1]$, por definición, tenemos que el área de la región está dada como:
$$\int_{0}^{1}[e^{x}-x]dx=\int_{0}^{1}e^{x}dx-\int_{0}^{1}xdx=\left [ e^{x} \right ]\bigg|_{0}^{1}-\left [ \frac{x^{2}}{2} \right ]\bigg|_{0}^{1}=e-1-\frac{1}{2}$$
por lo que el área es: $$A=e-1.5$$
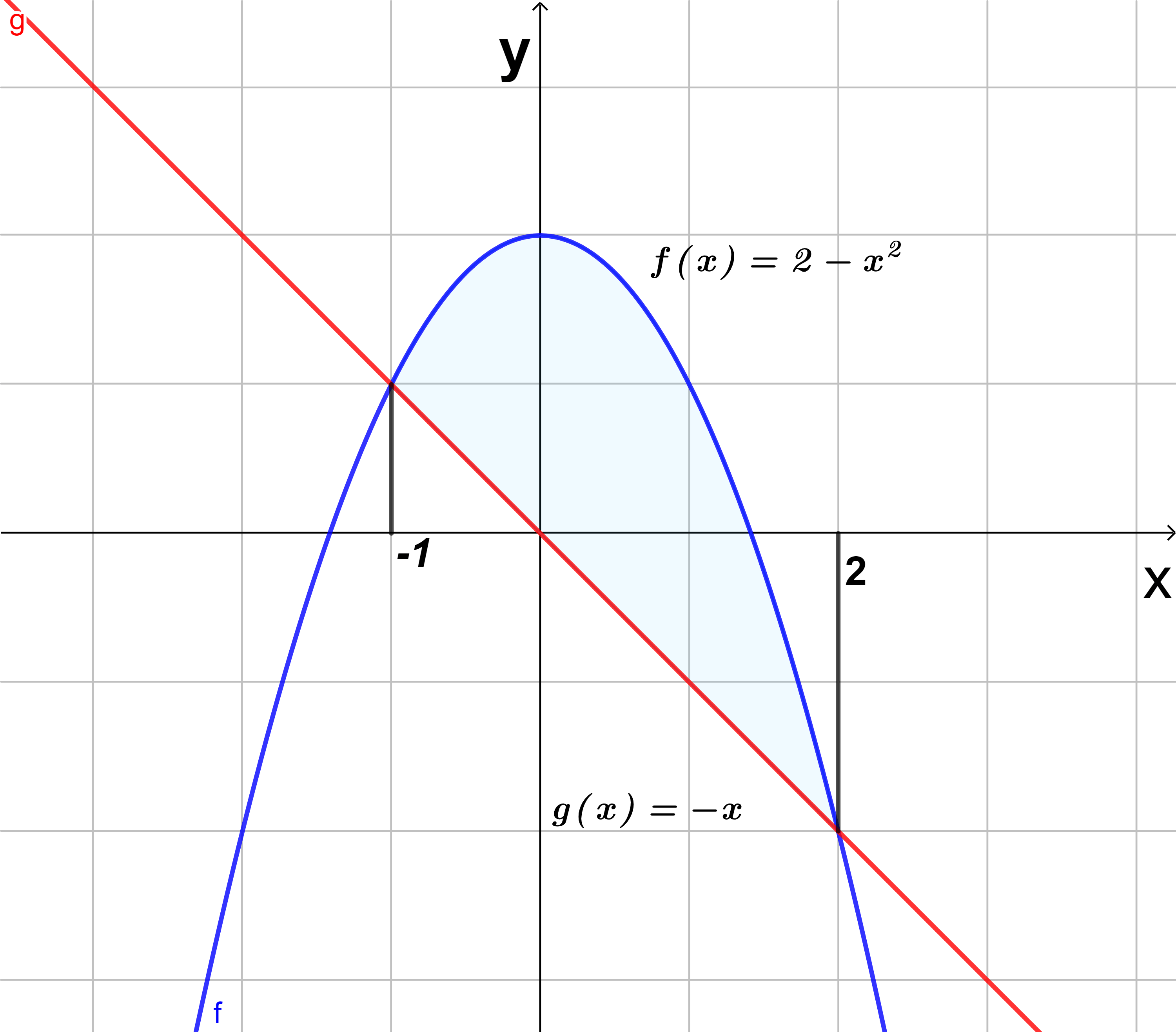
- Encontrar el área de la región acotada por la parábola $y=2-x^{2}$ y la recta $y=-x$
En este caso tenemos que encontrar los límites de integración, para saber de donde a donde vamos a integrar, para eso igualamos las dos funciones:
$$2-x^{2}=-x \Rightarrow x^{2}-x-2=0 \Rightarrow (x+1)(x-2)=0$$
Por lo que la región a integrar va de $x=-1$ a $x=2$, a veces es necesario graficar las funciones para ver quien es $f(x)$ y $g(x)$ en el intervalo deseado, ya que podríamos tener un área negativa si intercambiamos las funciones que no corresponden, de la figura $(3)$, vemos que $f(x)=2-x^{2}$ y $g(x)=-x$, así el área entre las curvas es:
$$\int_{-1}^{2}[2-x^{2}+x]dx=\int_{-1}^{2}2dx-\int_{-1}^{2}x^{2}dx+\int_{-1}^{2}xdx=\left [ 2x-\frac{x^{3}}{3}+\frac{x^{2}}{2} \right ]\bigg|_{-1}^{2}=(4-\frac{8}{3}+2)-(-2+\frac{1}{3}+\frac{1}{2})=\frac{9}{2}$$
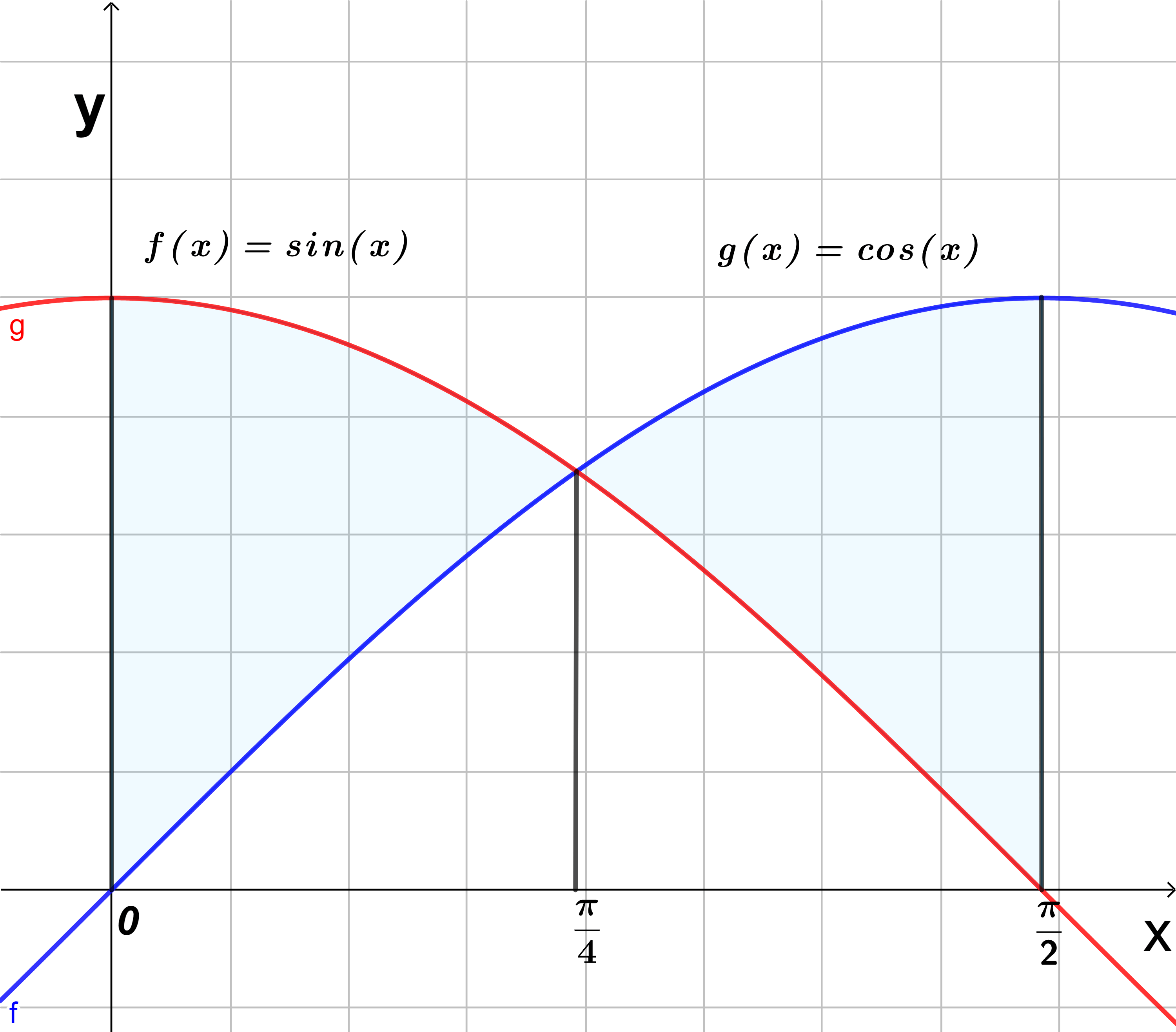
- Calcule el área de la región acotada entre las curvas $y=\cos(x)$, $y=\sin(x)$ y las rectas $x=0$ y $x=\frac{\pi }{2}$
De la figura vemos que: $\cos(x) \geq \sin(x)$ cuando $0 \leq x \leq \frac{\pi }{4}$ y $\sin(x) \geq \cos(x)$ cuando $\frac{\pi }{4} \leq x \leq \frac{\pi }{2}$ por lo que dividimos el área total como: $A=A_{1}+A_{2}$ y las integrales quedan de la siguiente forma:
$$A=A_{1}+A_{2}=\int_{0}^{\frac{\pi }{4}}[\cos(x)-\sin(x)]dx+\int_{\frac{\pi }{4}}^{\frac{\pi }{2}}[\sin(x)-\cos(x)]dx=\left [ \sin(x)+\cos(x) \right ]\bigg|_{0}^{\frac{\pi }{4}}+\left [ -\cos(x)-\sin(x) \right ]\bigg|_{\frac{\pi }{4}}^{\frac{\pi }{2}}$$
$$=(\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}}-0-1)+(-0-1+\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}})=2\sqrt{2}-2$$
Tarea moral
Los siguientes ejercicios no son para evaluación, pero son ejercicios para que practiques lo aprendido que te ayudaran en el desarrollo del entendimiento del tema, por lo que te invitamos a resolver los siguientes ejercicios propuestos relacionados con el tema visto.
A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.
- Encontrar el área de la región delimitada por la curva $y=x\sqrt{4-x^{2}}$ en el intervalo $[-2, 2]$
- Encontrar el área de la región delimitada por las curvas $y=1$ y $y=\cos^{2}(x)$ en el intervalo $[0, \pi]$
- Encontrar el área de la región delimitada por las curvas $y=\sqrt{x}$ y $y=x-2$
- Encontrar el área de la región delimitada por las curvas $y=x^{2}$ y $y=2-x$ en el intervalo $[0, 2]$
- Encontrar el área de la región delimitada por las curvas $y=\cos(x)$ y $y=\sin(x)$ en el intervalo $[0, 2\pi]$
Más adelante…
En esta sección deducimos la forma de calcular el área que está delimitada entre dos funciones mediante la aplicación de la fórmula deducida. La integral tiene más aplicaciones que solo calcular el área de la integral de una función, en la siguiente sección veremos ahora como calcular la longitud del arco de una función en un intervalo dado.
Entradas relacionadas
- Ir a Cálculo Diferencial e Integral II.
- Entrada anterior del curso: Cálculo Diferencial e Integral II: Criterios de convergencia para las integrales impropias. – El blog de Leo (nekomath.com)
- Siguiente entrada del curso: Cálculo Diferencial e Integral II: Longitud de arco – El blog de Leo (nekomath.com)