Introducción
Anteriormente se dio la definición de sucesión y revisamos algunos ejemplos. En esta entrada, se definirá la convergencia para una sucesión y se darán varios ejemplos de sucesiones convergentes y no convergentes.
Límite de una sucesión
A continuación daremos la definición de límite de una sucesión:
Definición. Sea $\{ a_n \}$ una sucesión en $\mathbb{R}$. Sea $L \in \mathbb{R}$, decimos que $L$ es el límite de la sucesión $\{a_n\}$ si para todo $ \varepsilon > 0$ existe un número natural $n_0$ tal que para todo $n \geq n_0$ se satisface $ | a_n – L |< \varepsilon$.
Si una sucesión tiene como límite a $L$, también decimos que converge a $L$ y lo denotamos como $$\lim_{n\to \infty} a_n = L.$$
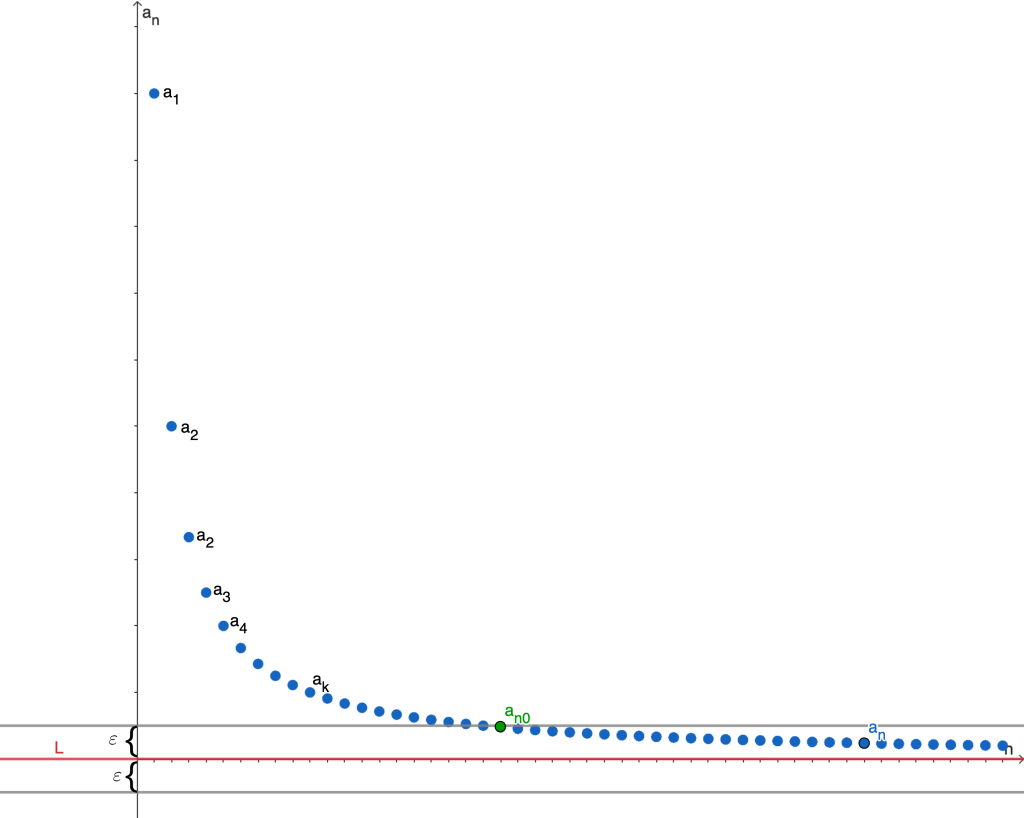
En términos más simples, la definición nos indica que una sucesión es convergente a $L$ si a partir de cierto elemento en la sucesión, $a_{n_0}$, los términos están lo suficientemente cerca, $\varepsilon$, de $L$. Para ilustrar estos elementos, a continuación se presenta la gráfica de la sucesión $\{a_n\} = \{ \frac{1}{n} \}$, y más adelante probaremos que converge a $L = 0$.
Observación. Cada punto de la gráfica está determinado por las coordenadas $(i, a_i)$ con $i \in \mathbb{N}$, pero por simplicidad, se denotan únicamente como $a_i$.
Ejemplos de sucesiones convergentes
Ahora continuaremos con algunos ejemplos de sucesiones convergentes. Es importante recalcar que para demostrar que una sucesión converge a $L$, deberemos especificar las condiciones que $n_0$ debe cumplir tal que para un $\varepsilon > 0$ arbitrario dado, $| a_n – L |< \varepsilon$ para todo $n \geq n_0$.
Ejemplo 1. Sea $k$ un número real y consideremos la sucesión $\{ a_n \} = \{k\}$, entonces $$\lim_{n \to \infty} k = k.$$
Demostración.
Sea $\varepsilon > 0$ (establecemos el valor arbitrario de un épsilon positivo).
Para esta sucesión cualquier valor de $n_0$ sirve, en particular consideremos $n_0 = 1$ (en este caso se puede dar $n_0 $ explícitamente).
Si $n \geq n_0 = 1$, entonces
\begin{gather*}
|a_n-k| = |k-k| = 0 < \varepsilon. \\
\therefore \lim_{n \to \infty} k = k.
\end{gather*}
$\square$
El ejemplo anterior es uno sencillo, sin embargo, como lo podemos ver en los comentarios entre paréntesis, están presentes los pasos relevantes para demostrar la convergencia. En este caso, dado que nuestra sucesión era un valor constante, el valor de $n_0$ que funcionaba era cualquier número natural, pero, en la mayoría de los casos, su valor estará definido en términos de épsilon.
Ejemplo 2. Consideremos la sucesión $\{ \frac{1}{n} \}$, entonces $$\lim_{n \to \infty} \frac{1}{n} = 0.$$
Demostración.
Sea $\varepsilon >0$.
Dado que el valor de $\varepsilon$ es positivo, por la propiedad Arquimediana, existe $n_0 \in \mathbb{N}$ tal que $1 < n_0 \cdot \varepsilon$, es decir, $\frac{1}{n_0} < \varepsilon$. Así, para cualquier $n \geq n_0$ se tiene que $\frac{1}{n} \leq \frac{1}{n_0} < \varepsilon $. De lo anterior se sigue que
$| \frac{1}{n} – 0| = \frac{1}{n} < \varepsilon.$
$\therefore | \frac{1}{n} – 0| < \varepsilon$ para todo $n \geq n_0.$
$$\therefore \lim_{n \to \infty} = 0.$$
$\square$
En este último ejemplo podemos observar cómo se establecen condiciones que $n_0$ debe cumplir en función de $\varepsilon$, así como la relevancia de la propiedad Arquimediana que estará constantemente presente al momento de demostrar convergencia mediante su definición.
Ejemplo 3. Demuestra que
$$\lim_{n \to \infty} \frac{8n-5}{3n} = \frac{8}{3}.$$
Demostración.
Sea $\varepsilon > 0$.
Notemos que
$$\left\lvert \frac{8n-5}{3n} – \frac{8}{3} \right\rvert = \left\lvert \frac{8n-5-8n}{3n} \right\rvert = \left\lvert \frac{-5}{3n} \right\rvert = \frac{5}{3n}.$$
\begin{align*}
\therefore \left\lvert \frac{8n-5}{3n} – \frac{8}{3} \right\rvert = \frac{5}{3n}. \tag{1}
\end{align*}
Consideremos $n_0 \cdot \varepsilon > \frac{5}{3}$, que sabemos que existe gracias a la propiedad Arquimediana. De esta forma, se tiene que
$$\varepsilon > \frac{5}{3n_0}.$$
Si $n \geq n_0$, entonces tenemos
\begin{align*}
\left\lvert \frac{8n-5}{3n} – \frac{8}{3} \right\rvert =& \frac{5}{3n}, \text{ por (1)} \\
\leq & \frac{5}{3n_0}, \text{ pues }n \geq n_0 \\
<& \varepsilon.
\end{align*}
$$\therefore \left\lvert \frac{8n-5}{3n} – \frac{8}{3} \right\rvert < \varepsilon.$$
$$\therefore \lim_{n \to \infty} \frac{8n-5}{3n} = \frac{8}{3}.$$
$\square$
Ejemplo 4. $$\lim_{n \to \infty} \left( \sqrt{n+1}-\sqrt{n} \right) = 0.$$
Demostración.
Sea $\varepsilon > 0$. Para simplificar la expresión, multiplicaremos por un uno haciendo uso del conjugado de la expresión anterior.
\begin{align*}
\sqrt{n+1}-\sqrt{n} =& (\sqrt{n+1}-\sqrt{n}) \cdot \frac{\sqrt{n+1}+\sqrt{n}}{\sqrt{n+1}+\sqrt{n}} \\ \\
=& \frac{\sqrt{n+1} ^ 2 – \sqrt{n}^2}{\sqrt{n+1}+\sqrt{n}} \\ \\
=& \frac{n+1 – n}{\sqrt{n-1}+\sqrt{n}} \\ \\
=&\frac{1}{\sqrt{n-1}+\sqrt{n}} \\ \\
\leq & \frac{1}{\sqrt{n}}.
\end{align*}
$$\therefore \sqrt{n-1}-\sqrt{n} \leq \frac{1}{\sqrt{n}}.$$
Consideremos $n_0 > \frac{1}{\varepsilon^2} \Rightarrow \frac{1}{\sqrt{n_0}} < \varepsilon$. Entonces tenemos
\begin{align*}
\left\lvert \sqrt{n-1}-\sqrt{n} – 0 \right\rvert =& \frac{1}{\sqrt{n-1}+\sqrt{n}} \text{, por la observación anterior} \\
\leq & \frac{1}{\sqrt{n}} \\
\leq & \frac{1}{\sqrt{n_0}}, \text{pues } n \geq n_0 \\
< & \varepsilon.
\end{align*}
$\therefore |\sqrt{n-1}-\sqrt{n} – 0| < \varepsilon.$
$$\therefore \lim_{n \to \infty} \left(\sqrt{n+1}-\sqrt{n} \right)= 0.$$
$\square$
Los dos ejemplos de arriba hacen uso de manipulaciones algebraicas que nos permiten simplificar nuestro problema; esta técnica de simplificación de expresiones, cuyo fin es llevarlas a otras más sencillas, es ampliamente usada para demostrar la convergencia de sucesiones.
Ejemplos de sucesiones no convergentes
Después de haber revisado ejemplos de sucesiones convergentes, vale la pena conocer sucesiones que no convergen, es decir, que su límite no existe.
Ejemplo 5. Consideremos la sucesión $\{ a_n \} = \{ (-1)^n \}$. Probaremos que el límite de $\{a_n\}$ no existe.
Demostración.
Procederemos a hacer esta demostración por contradicción. Supongamos que existe $L \in \mathbb{R}$ tal que $$\lim_{n \to \infty} (-1)^n = L.$$
Consideremos $\varepsilon = 1/2 > 0$. Por definición, existe $n_0 \in \mathbb{N}$ tal que si $n\geq n_0$ entonces $|(-1)^n-L| < \frac{1}{2}.$
Como $2n_0 > n_0$ y $2n_0+1>n_0$, entonces
\begin{gather*}
|(-1)^{2n_0}-L| < \frac{1}{2} \Rightarrow |1-L|< \frac{1}{2}. \tag{1} \\
|(-1)^{2n_0+1}-L| < \frac{1}{2} \Rightarrow |-1-L| = |1+L|< \frac{1}{2}. \tag{2}
\end{gather*}
Y notemos que
\begin{align*}
2 = |1+1| =& |1-L+L+1| \\
\leq & |1-L| + |1+L| \\
< & \frac{1}{2} + \frac{1}{2} \text{, por (1) y (2).}
\end{align*}
Lo anterior implica que $2<1$ y esto es una contradicción.
Por tanto, podemos concluir que tal límite no existe.
$\square$
Ahora estudiaremos una nueva definición para un tipo particular de sucesiones que no tienen como límite a un número real $L$.
Definición. Sea $\{a_n\}$ una sucesión en $\mathbb{R}$. Decimos que $\{a_n\}$ diverge a infinito si $\forall M \in \mathbb{R}$ existe $n_0 \in \mathbb{N}$ tal que si $n \geq n_0$ entonces $M < a_n$.
La definición anterior nos indica que una sucesión diverge a infinito si para cualquier número real $M$, existe un término de la sucesión $a_{n_0}$ a partir del cual todos los valores subsecuentes en la sucesión son mayores que $M$. Cuando una sucesión $\{ a_n \}$ diverja a infinito lo denotaremos como $$\lim_{n \to \infty} a_n = \infty.$$
Ejemplo 6. La sucesión $\{a_n\} = \{n\}$ diverge a infinito.
Demostración.
Sea $M \in \mathbb{N}$. Sabemos que $\mathbb{N}$ no está acotado superiormente, entonces existe $n_0 \in \mathbb{N}$ tal que $M< n_0$, de esta forma, si $n \geq n_0$, se tiene que $M<n$.
$\square$
Ejemplo 7. $$\lim_{n \to \infty} n^2 = \infty.$$
Demostración.
Procederemos a hacer la prueba por contradicción. Supongamos que para todo $n\in \mathbb{N}$ se tiene que $n^2 \leq M$ para algún $M \in \mathbb{R}$. Se sigue que
$\sqrt{n^2} \leq \sqrt{M}.$
Es decir,
$n \leq \sqrt{M}.$
Lo cual es una contradicción pues sabemos que el conjunto de los números naturales no está acotado superiormente.
$\therefore \{ n^2 \}$ diverge a infinito.
$\square$
Más adelante…
Se han revisado las definiciones de convergencia y divergencia a infinito, hemos visto diversos ejemplos de ambas definiciones. En las siguientes entradas se revisarán criterios para la convergencia de sucesiones, así como sus propiedades y teoremas con lo cual podremos determinar si una sucesión es convergente o no de manera más rápida.
Tarea moral
A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.
- Prueba que el límite de una sucesión convergente $\{ a_n \}$ es único.
Sugerencia:
1. Proceder por contradicción y asumir que existen dos números reales distintos $L$ y $L’$ tales que
$$\lim_{n \to \infty} a_n = L \quad \text{y} \quad \lim_{n \to \infty} a_n = L’.$$
2. Utilizar la definición de límite de una sucesión empleando el siguiente valor de épsilon: $$\varepsilon = \frac{|L-L’|}{2}.$$
$\varepsilon > 0$, ¿por qué? - Demuestra lo siguiente:
a) $$\lim_{n \to \infty} \frac{(-1)^n}{n} = 0.$$
b) $$\lim_{n \to \infty} \sqrt{n} = \infty.$$
c) $$\lim_{n \to \infty} \sqrt{12+ \frac{1}{n}} = \sqrt{12}.$$ - Sea $\{ a_n \}$ una sucesión en $\mathbb{R}$ y sea $L \in \mathbb{R}$. Prueba que $$\lim_{n \to \infty} a_n = L \Leftrightarrow \lim_{n \to \infty} a_n – L = 0.$$
- Una sucesión también puede ser divergente a $-\infty$. Propón una definición análoga a la de divergencia a infinito y prueba que $$\lim_{n \to \infty} – \sqrt{n} = – \infty.$$
Entradas relacionadas
- Ir a Cálculo Diferencial e Integral I
- Entrada anterior del curso: Sucesiones de números reales
- Siguiente entrada del curso: Operaciones con sucesiones convergentes
- Resto de cursos: Cursos
Agradecimientos
Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»