Introducción
En la entrada anterior dimos una clasificación de los ceros y las singularidades de una función analítica, en particular de las singulares aisladas que como vimos pueden clasificarse en tres tipos: singularidades removibles, polos y singularidades esenciales.
Esta entrada corresponde con la última del curso. En ella definiremos el residuo de una función analítica y veremos el teorema del residuo, mediante el cual nos será posible evaluar integrales reales, tanto impropias como integrales definidas, de una manera sencilla.
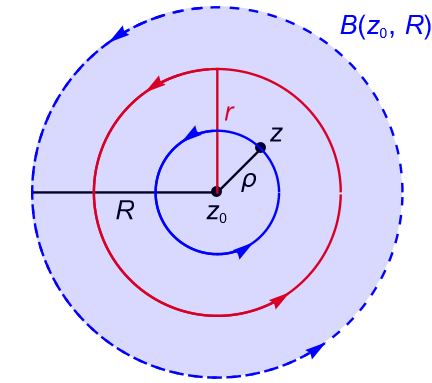
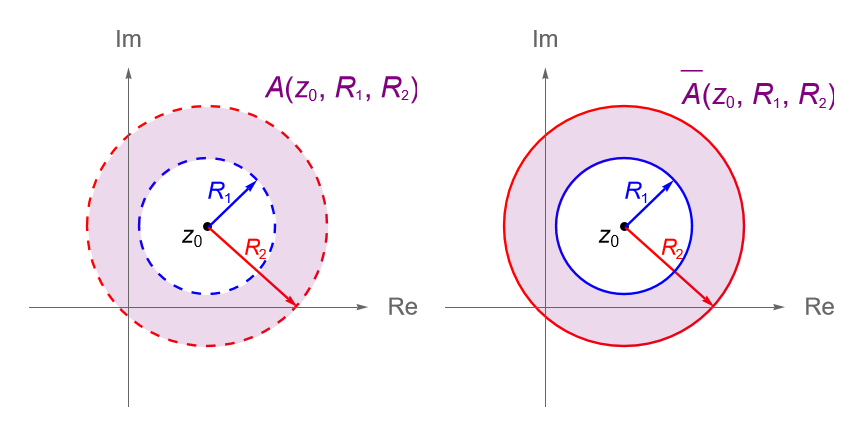
De acuerdo con la observación 42.5, sabemos que si $f$ es una función analítica en el disco abierto perforado $B^*(z_0,R)$, con $R>0$, y $z_0\in\mathbb{C}$ es una singularidad asilada de $f$, entonces para $0<r<R$, se cumple que la circunferencia $\gamma_r(t)=z_0+re^{it}$, con $t\in[0,2\pi]$, está contenida en el anillo $A(z_0,0,R) = B^*(z_0,R)$ y en dicho anillo $f$ tiene una expansión en serie de Laurent, por lo que:
\begin{equation*}
\int_{\gamma_r} f(z) dz = 2\pi i c_{-1},
\end{equation*}de donde:
\begin{equation*}
c_{-1} = \frac{1}{2\pi i}\int_{\gamma_r} f(z) dz, \tag{44.1}
\end{equation*}donde $0<r<R$.
Definición 44.1. (Residuo de una función analítica.)
Sean $f$ una función analítica en el disco abierto perforado $B^*(z_0,R)$, con $R>0$, y $z_0\in\mathbb{C}$ una singularidad asilada de $f$. El coeficiente $c_{-1}$ dado en (44.1) es llamado el {\bf residuo de $f$ en $z_0$} y se denota como:
\begin{equation*}
\operatorname{Res}(f,z_0) := c_{-1}.
\end{equation*}
Ejemplo 44.1.
De acuerdo con el ejemplo 42.7, para todo $z\in A(0,1,2)$, tenemos que:
\begin{equation*}
f(z) = \frac{1}{z^2-3z+2}= – \sum_{n=-\infty}^{-1} z^{n} -\sum_{n=0}^{\infty}\frac{z^n}{2^{n+1}} = – \sum_{n=-\infty}^{-2} z^{n} – \frac{1}{z} -\sum_{n=0}^{\infty}\frac{z^n}{2^{n+1}},
\end{equation*}por lo que $\operatorname{Res}(f,0) = -1$.
Por otra parte, del mismo ejemplo, para todo $z\in A(-i,\sqrt{2},\sqrt{5})$, tenemos que:
\begin{align*}
f(z) & = \frac{1}{z^2-3z+2}\\
& = -\sum_{n=-\infty}^{-1} \frac{\left(z+i\right)^{n}}{(1+i)^{n+1}} – \sum_{n=0}^{\infty} \frac{\left(z+i\right)^n}{(2+i)^{n+1}}\\
& = -\sum_{n=-\infty}^{-2} \frac{\left(z+i\right)^{n}}{(1+i)^{n+1}} – \frac{1}{z+i} – \sum_{n=0}^{\infty} \frac{\left(z+i\right)^n}{(2+i)^{n+1}},
\end{align*}por lo que $\operatorname{Res}(f,-i) = -1$.
Ejemplo 44.2.
Del ejemplo 42.8 tenemos que en $A(0,0,\infty)$ se cumple que:
\begin{equation*}
f(z) = e^{1/z} = \sum_{n=0}^\infty \frac{1}{ z^n \, n!},
\end{equation*}por lo que $\operatorname{Res}(f,0) = 1$.
Ejemplo 44.3.
Del ejemplo 42.9 tenemos que en $A(0,1,\infty)$ se cumple que:
\begin{equation*}
f(z) = \frac{1}{(1-z)^3} = -\frac{1}{2}\sum_{n=1}^\infty \frac{n(n+1)}{ z^{n+2}},
\end{equation*}por lo que $\operatorname{Res}(f,0) = 0$.
Procedemos a caracterizar al residuo de una función analítica.
Observación 44.1.
De acuerdo con la proposición 43.2, sabemos que si $f$ tiene una singularidad removible en $z_0$, entonces:
\begin{equation*}
f(z) = \sum_{n=0}^\infty c_n(z-z_0)^n, \quad \forall z \in B^*(z_0,R),
\end{equation*}por lo que $\operatorname{Res}(f,z_0) = c_{-1} = 0$. ¿Qué sucede si $z_0$ es un polo?
Proposición 44.1.
Sean $f$ una función analítica en $A(z_0,0,R)$, con $R>0$ y $z_0\in\mathbb{C}$ una singularidad aislada de $f$. Si $f$ tiene un polo de orden $m\in\mathbb{N}^+$ en $z_0$, entonces:
\begin{equation*}
\operatorname{Res}(f,z_0) = \frac{1}{(m-1)!} \lim_{z \to z_0} \frac{d^{m-1}}{dz^{m-1}} \left[(z-z_0)^m f(z)\right].
\end{equation*}
Si $z_0$ es un polo simple, es decir, $m=1$, entonces no hay diferenciación.
Demostración. Dadas las hipótesis, por la proposición 43.3(6) tenemos que:
\begin{equation*}
f(z)=\sum_{n=-m}^{\infty} c_n (z-z_0)^n, \quad \forall z\in A(z_0,0,R).
\end{equation*}
Entonces, para $z\in A(z_0,0,R)$ tenemos que:
\begin{equation*}
(z-z_0)^m f(z)=\sum_{n=0}^{\infty} c_{n-m} (z-z_0)^n.
\end{equation*}
Por la convergencia uniforme de la serie de potencias, teorema 39.2, tenemos que:
\begin{align*}
\frac{d^{m-1}}{dz^{m-1}} (z-z_0)^m f(z) & = \frac{d^{m-1}}{dz^{m-1}}\sum_{n=0}^{\infty} c_{n-m} (z-z_0)^n\\
& = \sum_{n=0}^{\infty} \frac{d^{m-1}}{dz^{m-1}} c_{n-m} (z-z_0)^n\\
& = \sum_{n=m-1}^{\infty} \frac{n!}{(n-m+1)!} c_{n-m} (z-z_0)^{n-m+1}\\
& = (m-1)! \,\, c_{-1} + \sum_{n=m}^{\infty} \frac{n!}{(n-m+1)!} c_{n-m} (z-z_0)^{n-m+1}.
\end{align*}
Entonces:
\begin{equation*}
\lim_{z\to z_0} \frac{d^{m-1}}{dz^{m-1}} (z-z_0)^m f(z) = (m-1)! \,\, c_{-1} + 0,
\end{equation*}de donde:
\begin{equation*}
\operatorname{Res}(f,z_0) = c_{-1} = \frac{1}{(m-1)!} \lim_{z \to z_0} \frac{d^{m-1}}{dz^{m-1}} \left[(z-z_0)^m f(z)\right].
\end{equation*}
$\blacksquare$
Corolario 44.1.
Sean $f$ una función analítica en $A(z_0,0,R)$, con $R>0$ y $z_0\in\mathbb{C}$ una singularidad aislada de $f$.
- $f$ tiene un polo simple en $z_0$ si y solo si:
\begin{equation*}
\operatorname{Res}(f,z_0) = \lim_{z \to z_0} f(z) \neq 0.
\end{equation*} - Si $f(z) = \dfrac{p(z)}{q(z)}$, donde $p$ y $q$ son analíticas en $z_0$, $p(z_0) \neq 0$ y $q$ tiene un cero simple en $z_0$, entonces:
\begin{equation*}
\operatorname{Res}(f,z_0) = \operatorname{Res}\left(\dfrac{p}{q},z_0\right) = \dfrac{p(z_0)}{q'(z_0)}.
\end{equation*}
Demostración. Dadas las hipótesis, tenemos:
- $\Rightarrow)$ Por la proposición 43.3(3) y la la proposición 44.1, tenemos que:
\begin{equation*}
0 \neq \lim_{z \to z_0} (z-z_0) f(z) = \operatorname{Res}(f,z_0).
\end{equation*}$(\Leftarrow$ Por la definición 44.1, tenemos que:
\begin{equation*}
c_{-1} = \operatorname{Res}(f,z_0) = \lim_{z \to z_0} (z-z_0) f(z) \neq 0,
\end{equation*}por lo que el resultado se sigue de la proposición 43.3. - Como $q$ tiene un cero simple en $z_0$, entonces, $q'(z_0) \neq 0$, proposición 43.1(2). Más aún, por el ejercicio 7 de la entrada anterior, tenemos que $1/q$ tiene un polo simple en $z_0$, por lo que $f$ tiene un polo simple en $z_0$, ya que $p(z_0) \neq 0$, entonces, como $q(z_0) = 0$, del inciso anterior se sigue que:
\begin{align*}
\operatorname{Res}\left(\dfrac{p}{q},z_0\right) & = \operatorname{Res}(f,z_0)\\
& = \lim_{z \to z_0} (z-z_0) \dfrac{p(z)}{q(z)}\\
& = \lim_{z \to z_0} \dfrac{p(z)}{\dfrac{q(z) – q(z_0)}{z-z_0}}\\
& = \dfrac{p(z_0)}{q'(z_0)}.
\end{align*}
$\blacksquare$
Ejemplo 44.4.
Determinemos el residuo de la función $f(z) = \left(\dfrac{z+1}{z-1}\right)^3$, en la singularidad aislada $z_0=1$.
Solución. Notemos que para $z\neq 1$ se tiene que:
\begin{equation*}
(z-1)^3 f(z) = (z+1)^3
\end{equation*}de donde:
\begin{equation*}
\lim_{z \to 1} (z-1)^3 f(z) = \lim_{z \to 1} (z+1)^3 = 8 \neq 0,
\end{equation*}por lo que, proposición 43.3(3), $z_0 =1$ es un polo de orden $3$.
De la proposición 44.1 se sigue que:
\begin{align*}
\operatorname{Res}(f,1) & = \frac{1}{2!} \lim_{z \to 1} \frac{d^2}{dz^2} (z-1)^3 f(z)\\
& = \frac{1}{2} \lim_{z \to 1} \frac{d^2}{dz^2} (z+1)^3\\
& = \frac{1}{2} \lim_{z \to 1} 6(z+1)\\
& = \frac{12}{2}\\
& =6.
\end{align*}
Ejemplo 44.5.
Sea $f(z) = \dfrac{1}{z^4+1}$. Es claro que $f$ tiene como singularidades aisladas a las cuatro raíces de $-1$. Por la proposición 5.1, sabemos que dichas raíces están dadas por:
\begin{equation*}
z_k = \operatorname{cis}\left(\frac{\pi+2\pi k}{4}\right) = \operatorname{exp}\left(i\left[\frac{\pi+2\pi k}{4}\right]\right), \quad k=0,1,2,3.
\end{equation*}
Tenemos que $z_0 = e^{i\pi/4}, z_1 = e^{i3\pi/4}, z_2 = e^{i5\pi/4}$ y $z_3 = e^{i7\pi/4}$, por lo que:
\begin{equation*}
f(z) = \dfrac{1}{z^4+1} = \dfrac{1}{(z-z_0)(z-z_1)(z-z_2)(z-z_3)}.
\end{equation*}
Es claro que para $k=0,1,2,3$ se cumple que:
\begin{equation*}
\lim_{z \to z_0} (z-z_k) f(z) \neq 0,
\end{equation*}por lo que, proposición 43.3, las cuatro raíces son polos simples de $f$.
Procedemos a determinar sus residuos considerando el corolario 44.1(2). sean $p(z)=1$ y $q(z) = z^4+1$. Tenemos que $q'(z) = 4z^3$, por lo que:
\begin{align*}
\operatorname{Res}(f,z_0) &= \frac{1}{q'(z_0)} = \frac{1}{4(e^{i\pi/4})^3} = \frac{1}{4} e^{-i3\pi/4} = -\frac{1}{4\sqrt{2}} – i\frac{1}{4\sqrt{2}}.\\
\operatorname{Res}(f,z_1) &= \frac{1}{q'(z_1)} = \frac{1}{4(e^{i3\pi/4})^3} = \frac{1}{4} e^{-i9\pi/4} = \frac{1}{4\sqrt{2}} – i\frac{1}{4\sqrt{2}}.\\
\operatorname{Res}(f,z_2) &= \frac{1}{q'(z_2)} = \frac{1}{4(e^{i5\pi/4})^3} = \frac{1}{4} e^{-i15\pi/4} = -\frac{1}{4\sqrt{2}} +i\frac{1}{4\sqrt{2}}.\\
\operatorname{Res}(f,z_3) &= \frac{1}{q'(z_0)} = \frac{1}{4(e^{i7\pi/4})^3} = \frac{1}{4} e^{-i21\pi/4} = -\frac{1}{4\sqrt{2}} + i\frac{1}{4\sqrt{2}}.
\end{align*}
Teorema 44.1. (Teorema del Residuo.)
Sean $D\subset\mathbb{C}$ un dominio y $f:D\to\mathbb{C}$ una función analítica en $D$ excepto por un número finito de singularidades aisladas (distintas) $z_1, z_2, \ldots, z_n \in D$. Si $\gamma$ es un contorno cerrado simple en $D\setminus\{z_1, z_2, \ldots, z_n\}$ tal que $n(\gamma,z) = 0$ para todo $z\in \mathbb{C}\setminus D$, entonces:
\begin{equation*}
\frac{1}{2\pi i} \int_{\gamma} f(z) dz = \sum_{k=1}^n \operatorname{Res}(f,z_k) \, n(\gamma, z_k).
\end{equation*}
Demostración. Dadas las hipótesis, como las singularidades son aisladas, dado $k\in \{1,\ldots, n\}$, existe $r_k>0$ tal que $f$ tiene una expansión en serie de Laurent:
\begin{equation*}
f(z) = \sum_{j=-\infty}^\infty c_j (z-z_k)^j, \quad \forall z\in A(z_k, 0, r_k).
\end{equation*}
Del corolario 39.1 tenemos que la función:
\begin{equation*}
g_k(z) := \sum_{j=-\infty}^{-1} c_j (z-z_k)^j,
\end{equation*}es analítica en $\mathbb{C}\setminus\{z_k\}$.
Notemos que:
\begin{equation*}
\lim_{z\to z_k} (z-z_k) \left[f(z)- g_k(z)\right] = 0,
\end{equation*}por lo que, proposición 43.3(6), $f-g_k$ tiene una singularidad removible en $z_k$.
Del ejemplo 34.2, para toda $j\leq -2$ tenemos que:
\begin{equation*}
\int_{\gamma} (z-z_k)^j dz = 0.
\end{equation*}
Entonces, por la convergencia uniforme de la serie que define a $g_k$, proposición 39.1, y las definiciones 36.1 y 44.1, tenemos que:
\begin{align*}
\frac{1}{2\pi i} \int_{\gamma} g_k(z) dz & = \frac{1}{2\pi i} \int_{\gamma} \sum_{j=-\infty}^{-1} c_j (z-z_k)^j dz\\
& = \sum_{j=-\infty}^{-1} \frac{c_j}{2\pi i} \int_{\gamma} (z-z_k)^j dz\\
& = \frac{c_{-1}}{2\pi i} \int_{\gamma} \frac{1}{z-z_k} dz\\
& = \operatorname{Res}(f,z_k) \, n(\gamma, z_k).
\end{align*}
Consideremos ahora a la función:
\begin{equation*}
F(z):= f(z) – \sum_{k=1}^n g_k(z), \quad \forall z \in D\setminus\{z_1, z_2, \ldots, z_n\}.
\end{equation*}
Dado $m \in \{1,\ldots, n\}$, sabemos que $f-g_m$ tiene una singularidad removible en $z_m$ y $g_k$ es una función definida y analítica en $z_m$ para todo $k\neq m$. Notemos que lo anterior se cumple para todo $m$, por lo que $F$ puede redefinirse de modo que sea una función analítica en $D$. Entonces, del teorema de Cauchy, versión homológica (teorema 38.4), como $n(\gamma,z)=0$ para todo $z\in \mathbb{C}\setminus D$, se tiene que:
\begin{equation*}
0 = \int_{\gamma} F(z) dz = \int_{\gamma} f(z) dz – \sum_{k=1}^n \int_{\gamma} g_k(z) dz.
\end{equation*}
De donde:
\begin{equation*}
\frac{1}{2\pi i} \int_{\gamma} f(z) dz = \sum_{k=1}^n \int_{\gamma} \frac{1}{2\pi i} g_k(z) dz = \sum_{k=1}^n \operatorname{Res}(f,z_k) \, n(\gamma, z_k).
\end{equation*}
$\blacksquare$
Una consecuencia inmediata de este resultado es el siguiente corolario. Sin embargo, considerando el teorema de Cauchy para dominios múltiplemente conexos, proposición 38.1, podemos dar una prueba sencilla del mismo.
Corolario 44.2. (Teorema del Residuo de Cauchy.)
Sean $D\subset\mathbb{C}$ un dominio, $C$ un contorno cerrado simple, orientado positivamente, contenido en $D$. Si $f$ es una función analítica en $D$, excepto por un número finito de singularidades aisladas (distintas) $z_1, z_2, \ldots, z_n$, las cuales están dentro de $C$, entonces:
\begin{equation*}
\int_{C} f(z)dz = 2\pi i \sum_{k=1}^n \operatorname{Res}(f,z_k).
\end{equation*}
Demostración. Dadas las hipótesis, como $D$ es abierto, entonces podemos tomar pequeñas circunferencias $\gamma_{k}(t) = z_k + r_k e^{it}$, con $t\in[0,2\pi]$, alrededor de la singularidad aislada $z_k$, tal que $\gamma_k$ está contenida dentro de $C$ y $\gamma_k$ no contiene a ninguna otra singularidad $z_j$ de $f$ si $j\neq k$.
Sea $\varepsilon>0$ tal que el disco abierto perforado $B^*(z_k,r_k+\varepsilon)$, no contiene a ninguna singularidad $z_j$ de $f$ si $j\neq k$. Entonces en $B^*(z_k,r_k+\varepsilon)$ la función $f$ tiene una representación en serie de Laurent y $\gamma_k$ está contenida en $B^*(z_k,r_k+\varepsilon)$. Por lo que, de la observación 42.5 y la definición 44.1, se sigue que:
\begin{equation*}
\int_{\gamma_k} f(z) dz = 2\pi i c_{-1} = 2\pi i \operatorname{Res}(f,z_k),
\end{equation*}para $k=1,\ldots, n$.
Por lo tanto, del teorema de Cauchy para dominios múltiplemente conexos, proposición 38.1, tenemos que:
\begin{equation*}
\int_{C} f(z) dz = \sum_{k=1}^n \int_{\gamma_k} f(z) dz = 2\pi i\sum_{k=1}^n \operatorname{Res}(f,z_k).
\end{equation*}
$\blacksquare$
Ejemplo 44.6.
Evaluemos la integral:
\begin{equation*}
\int_{\gamma} \frac{1}{z^4+1} dz,
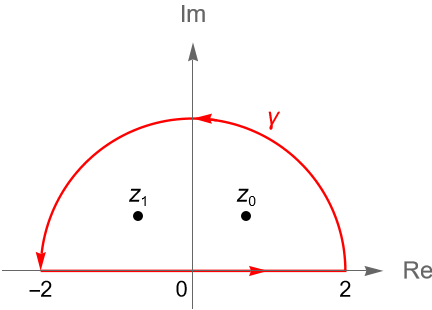
\end{equation*}donde $\gamma$ es el contorno cerrado simple de la figura 149.
Solución. Por el ejemplo 44.5 sabemos que $f$ tiene cuatro polos simples en los puntos $z_0 = e^{i\pi/4}, z_1 = e^{i3\pi/4}, z_2 = e^{i5\pi/4}$ y $z_3 = e^{i7\pi/4}$. Es claro que solo $z_0$ y $z_1$ están dentro del contorno $\gamma$, por lo que del teorema del residuo se sigue que:
\begin{align*}
\int_{\gamma} \frac{1}{z^4+1} dz & = 2\pi i \left(\operatorname{Res}(f,z_0) + \operatorname{Res}(f,z_1)\right)\\
& = 2\pi i \left(-\frac{1}{4\sqrt{2}} – i\frac{1}{4\sqrt{2}} + \frac{1}{4\sqrt{2}} – i\frac{1}{4\sqrt{2}}\right)\\
& = 2\pi i \left(-\frac{2i}{4\sqrt{2}}\right)\\
& = \frac{\pi}{\sqrt{2}}.
\end{align*}
Ejemplo 44.7.
Veamos que:
\begin{equation*}
\int_{\gamma} e^{1/z} dz = 2\pi i,
\end{equation*}donde $\gamma$ es la circunferencia unitaria orientada positivamente.
Solución. Por el ejemplo 43.5 sabemos que $f(z) = e^{1/z}$ tiene una singularidad esencial en $z_0 = 0$, por lo que no podemos recurrir a los resultados previos para determinar el residuo de $f$. Sin embargo, considerando el ejemplo 44.2, tenemos que el coeficiente $z^{-1}$ es $1$, por lo que $\operatorname{Res}(f,0)=1$.
Por el teorema del residuo, como $z_0 = 0$ es una singularidad aislada de $f$ y está dentro del contorno cerrado $\gamma$, tenemos que:
\begin{equation*}
\int_{\gamma} e^{1/z} dz = 2\pi i \operatorname{Res}(f,0) = 2\pi i(1) = 2\pi i.
\end{equation*}
Observación 44.2.
El teorema del residuo nos permite evaluar integrales reales muy particulares, analizamos los siguientes dos tipos.
- Integrales reales trigonométricas de la forma:
\begin{equation*}
\displaystyle \int_{0}^{2\pi} F(\operatorname{cos}(t),\operatorname{sen}(t)) dt,
\end{equation*}donde $F(\operatorname{cos}(t),\operatorname{sen}(t))$ es una función racional de $\operatorname{cos}(t)$ y $\operatorname{sen}(t)$ con coeficientes reales y cuyo denominador no se anula en el intervalo $[0,2\pi]$. Por ejemplo las integrales:
\begin{equation*}
\int_{0}^{2\pi} \frac{1}{2+\operatorname{cos}(t)} dt \quad \text{y} \quad \int_{0}^{2\pi} \frac{\operatorname{cos}^2(t)}{2+\operatorname{cos}(t)} dt,
\end{equation*}son de este tipo. - Integrales reales impropias del tipo:
\begin{equation*}
\displaystyle \int_{-\infty}^{b} f(t) dt, \quad \displaystyle \int_{a}^{\infty} f(t) dt, \quad \displaystyle \int_{-\infty}^{\infty} f(t) dt,
\end{equation*}donde $f$ es una función continua en el dominio de integración y $a,b\in\mathbb{R}$.
Para el primer tipo de integrales consideramos a la circunferencia unitaria orientada positivamente, es decir, $\gamma(t) = e^{it}$, con $t\in[0,2\pi]$.
Haciendo la sustitución $z=\gamma(t) = e^{it}$, con $0\leq t\leq 2\pi$, tenemos que $dt = \dfrac{dz}{iz}$. Considerano las definiciones de las funciones $\operatorname{sen}(t)$ y $\operatorname{sen}(t)$, tenemos que:
\begin{align*}
\operatorname{cos}(t) & = \dfrac{e^{it}+e^{-it}}{2} = \dfrac{z+\dfrac{1}{z}}{2},\\
\operatorname{sen}(t) & = \dfrac{e^{it}-e^{-it}}{2i} = \dfrac{z-\dfrac{1}{z}}{2i}.
\end{align*}
Entonces:
\begin{equation*}
\int_{0}^{2\pi} F(\operatorname{cos}(t),\operatorname{sen}(t)) dt = \int_{\gamma} \frac{1}{iz} F\left(\frac{1}{2}\left[z+\dfrac{1}{z}\right],\frac{1}{2i}\left[z-\dfrac{1}{z}\right]\right) dz.
\end{equation*}
Utilizando el teorema del residuo tenemos que:
\begin{equation*}
\int_{\gamma} \frac{1}{iz} F\left(\frac{1}{2}\left[z+\dfrac{1}{z}\right],\frac{1}{2i}\left[z-\dfrac{1}{z}\right]\right) dz = 2\pi i \sum,
\end{equation*}donde $\sum$ es la suma de los residuos de la función:
\begin{equation*}
\frac{1}{iz} F\left(\frac{1}{2}\left[z+\dfrac{1}{z}\right],\frac{1}{2i}\left[z-\dfrac{1}{z}\right]\right).
\end{equation*}
Ejemplo 44.8.
Evaluemos la integral:
\begin{equation*}
\int_{0}^{2\pi} [\operatorname{cos}^3(t) + \operatorname{sen}^2(t)] dt.
\end{equation*}
Solución. Tenemos que:
\begin{align*}
\operatorname{cos}^3(t) & = \left[\frac{1}{2}\left(z+\dfrac{1}{z}\right)\right]^3 = \frac{1}{8}\left(z^3+\dfrac{1}{z^3}+3z+\frac{3}{z}\right),\\
\operatorname{sen}^2(t) & = \left[\frac{1}{2i}\left(z-\dfrac{1}{z}\right)\right]^2 = -\frac{1}{4}\left(z^2+\dfrac{1}{z^2}-2\right),
\end{align*}de donde:
\begin{align*}
\operatorname{cos}^3(t) + \operatorname{sen}^2(t) & = \frac{1}{8}\left(z^3+\dfrac{1}{z^3}+3z+\frac{3}{z}\right) – \frac{1}{4}\left(z^2+\dfrac{1}{z^2}-2\right)\\
& = \frac{z^3}{8} +\dfrac{1}{8z^3} – \frac{z^2}{4} -\dfrac{1}{4z^2} +\frac{3z}{8} +\frac{3}{8z} +\frac{1}{2}\\
& = \frac{z^6-2z^5+3z^4+4z^3+3z^2-2z+1}{8z^3}.
\end{align*}
Consideremos a la siguiente función:
\begin{equation*}
f(z) = \frac{z^6-2z^5+3z^4+4z^3+3z^2-2z+1}{i8z^4}.
\end{equation*}
Es claro que $z_0 = 0$ es una singularidad aislada de $f$. Más aún, $z_0 = 0$ es un polo de orden $4$ ya que:
\begin{equation*}
\lim_{z\to 0} (z-0)^4 f(z) = \lim_{z\to 0} \frac{z^6-2z^5+3z^4+4z^3+3z^2-2z+1}{i8} = \frac{1}{8i} \neq 0.
\end{equation*}
Notemos que $z_0 = 0$ está dentro de la circunferencia unitaria $\gamma$, por lo que:
\begin{align*}
\operatorname{Res}(f,0) & = \frac{1}{3!} \lim_{z \to 0}\frac{d^3}{dz^3} (z-0)^4 f(z)\\
& = \frac{1}{6} \lim_{z \to 0}\frac{d^3}{dz^3} \left(\frac{z^6-2z^5+3z^4+4z^3+3z^2-2z+1}{i8}\right)\\
& = \frac{1}{6} \lim_{z \to 0} \left(\frac{120z^3-120z^2+72z+24}{i8}\right)\\
& = \frac{24}{48i}= -\frac{i}{2}.
\end{align*}
Entonces:
\begin{align*}
\int_{0}^{2\pi} [\operatorname{cos}^3(t) + \operatorname{sen}^2(t)] dt & = \int_{\gamma} \frac{1}{iz} \left[\frac{z^6-2z^5+3z^4+4z^3+3z^2-2z+1}{8z^3}\right] dz\\
& = \int_{\gamma} f(z) dz\\
& = 2\pi i \operatorname{Res}(f,0)\\
& =2 \pi i \left(-\frac{i}{2}\right)\\
& = \pi.
\end{align*}
Para el segundo tipo de integrales reales, recordemos que para una función $f$ continua en $(-\infty, b]$ y $[a, \infty)$, respectivamente, las integrales reales impropias se definen en términos de límites, es decir:
\begin{align*}
\displaystyle \int_{-\infty}^{b} f(t) dt & = \lim_{R \to \infty} \int_{-R}^{b} f(t) dt,\\
\displaystyle \int_{a}^{\infty} f(t) dt & = \lim_{R \to \infty} \int_{a}^{R} f(t) dt,
\end{align*}siempre que los límites existan, en tal caso las integrales se llaman convergentes, en caso contrario se dice que las integrales divergen.
Por otra parte, si $f$ es continua en $(-\infty, \infty)$ y las integrales impropias $\displaystyle \int_{-\infty}^{0} f(t) dt$ y $\displaystyle \int_{0}^{\infty} f(t) dt $ existen, entonces la integral $\displaystyle \int_{-\infty}^{\infty} f(t) dt $ es convergente y está dada por:
\begin{equation*}
\displaystyle \int_{-\infty}^{\infty} f(t) dt = \lim_{R \to \infty} \int_{-R}^{0} f(t) dt + \lim_{R \to \infty} \int_{0}^{R} f(t) dt.
\end{equation*}
Definición 44.2. (Valor principal de Cauchy.)
Se define el valor principal de Cauchy de la integral impropia $ \displaystyle \int_{-\infty}^{\infty} f(t) dt$ como:
\begin{equation*}
\text{P.V.} \displaystyle \int_{-\infty}^{\infty} f(t) dt = \lim_{R \to \infty} \int_{-R}^{R} f(t) dt,
\end{equation*}si el límite existe.
Observación 44.3.
El valor principal de Cauchy de una integral puede existir incluso si la integral impropia es divergente. Por ejemplo:
\begin{equation*}
\int_{-R}^{R} t dt = \frac{R^2}{2} – \left(-\frac{R^2}{2}\right) = 0,
\end{equation*}por lo que:
\begin{equation*}
\text{P.V.} \displaystyle \int_{-\infty}^{\infty} t dt = \lim_{R \to \infty} \int_{-R}^{R} t dt = 0.
\end{equation*}
Sin embargo, la integral impropia de $f(t)=t$, en $(-\infty,\infty)$, es divergente, ya que:
\begin{equation*}
\displaystyle \int_{0}^{\infty} t dt = \lim_{R \to \infty} \int_{0}^{R} t dt = \lim_{R \to \infty} \frac{R^2}{2} = \infty.
\end{equation*}
Cuando una integral impropia $\displaystyle \int_{-\infty}^{\infty} f(t) dt$ es convergente, entonces existe su valor principal de Cauchy y ambas integrales son iguales, ya que:
\begin{align*}
\text{P.V.} \displaystyle \int_{-\infty}^{\infty} f(t) dt & = \lim_{R \to \infty} \int_{-R}^{R} f(t) dt\\
& = \lim_{R \to \infty} \left[\int_{-R}^{0} f(t) dt + \int_{0}^{R} f(t) dt\right]\\
& = \lim_{R \to \infty} \int_{-R}^{0} f(t) dt + \lim_{R \to \infty} \int_{0}^{R} f(t) dt\\
& = \displaystyle \int_{-\infty}^{\infty} f(t) dt.
\end{align*}
Entonces, al evaluar integrales impropias utilizando integrales de contorno debe ser claro que estamos calculando su valor principal de Cauchy, y si dicha integral existe entonces coincidirá con el valor obtenido por este método.
Para evaluar un integral impropia $ \displaystyle \int_{-\infty}^{\infty} f(t) dt$, donde $f$ es una función racional continua en $(-\infty,\infty)$, reemplazamos a la variable real $t$ por la variable compleja $z$ e integramos a $f$ sobre un contorno cerrado $\gamma$, orientado positivamente, que consiste del intervalo real $[-R,R]$ en el eje $x$ y una semicircunferencia $C_R$ de radio $R$ suficientemente grande para que los polos de $f$ estén en el interior de $\gamma$, como en la figura 149, en el semiplano superior $\operatorname{Im}(z)>0$.
Entonces, por la proposición 34.2(3) y el teorema del residuo, tenemos que:
\begin{equation*}
\int_{\gamma} f(z) dz = \int_{C_R} f(z) dz + \int_{-R}^{R} f(z) dz = 2\pi i \sum_{k=1}^n \operatorname{Res}(f,z_k),
\end{equation*}donde $z_k$, con $k=1,\ldots, n$, denota a los polos en el semiplano superior $\operatorname{Im}(z)>0$.
Por lo tanto, si se muestra que:
\begin{equation*}
\lim_{R \to \infty} \int_{C_R} f(z) dz = 0,
\end{equation*}entonces tenemos que:
\begin{equation*}
\text{P.V.} \displaystyle \int_{-\infty}^{\infty} f(t) dt = \lim_{R \to \infty} \int_{-R}^{R} f(t) dt = 2\pi i \sum_{k=1}^n \operatorname{Res}(f,z_k).
\end{equation*}
Ejemplo 44.9.
Determinemos el valor principal de Cauchy de la integral impropia:
\begin{equation*}
\displaystyle \int_{-\infty}^{\infty} \frac{1}{(t^2+1)(t^2+9)}dt.
\end{equation*}
Solución. Sea:
\begin{equation*}
f(z) = \frac{1}{(z^2+1)(z^2+9)} = \frac{1}{(z-i)(z+i)(z-3i)(z+3i)}.
\end{equation*}
Dado que $z_1 = i$ y $z_2 = 3i$ son los dos polos simples en el semiplano superior $\operatorname{Im}(z)>0$, entonces podemos tomar a $\gamma$ como el contorno cerrado formado por el intervalo real $[-R,R]$ y la semicircunferencia $C_R(t)=Re^{it}$, con $t\in[0,\pi]$, para $R>3$, como en la figura 149.
Por la proposición 34.2(3) y el teorema del residuo, tenemos que:
\begin{align*}
\int_{\gamma} f(z) dz & = \int_{C_R} \frac{1}{(z^2+1)(z^2+9)} dz + \int_{-R}^{R} \frac{1}{(t^2+1)(t^2+9)} dt\\
& = 2\pi i \sum_{k=1}^2 \operatorname{Res}(f,z_k)\\
& = 2\pi i\left[\operatorname{Res}(f,z_1) + \operatorname{Res}(f,z_2)\right].
\end{align*}
Para los polos simples $z_1=i$ y $z_2=3i$, por la proposición 44.1 tenemos que:
\begin{align*}
\operatorname{Res}(f,z_1) & = \lim_{z \to z_1} (z-z_1) f(z)\\
& = \lim_{z \to i} (z-i)\frac{1}{(z-i)(z+i)(z-3i)(z+3i)}\\
& = \lim_{z \to i} \frac{1}{(z+i)(z-3i)(z+3i)}\\
& = \frac{1}{16i},
\end{align*}
\begin{align*}
\operatorname{Res}(f,z_2) & = \lim_{z \to z_2} (z-z_2) f(z)\\
& = \lim_{z \to 3i} (z-3i)\frac{1}{(z-i)(z+i)(z-3i)(z+3i)}\\
& = \lim_{z \to 3i} \frac{1}{(z-i)(z+i)(z+3i)}\\
& = -\frac{1}{48i},
\end{align*}por lo que:
\begin{equation*}
\int_{C_R} \frac{1}{(z^2+1)(z^2+9)} dz + \int_{-R}^{R} \frac{1}{(t^2+1)(t^2+9)} dt = 2\pi i\left[\frac{1}{16i} -\frac{1}{48i}\right] = \frac{\pi}{12}.
\end{equation*}
Notemos que:
\begin{equation*}
|(z^2+1)(z^2+9)| = |z^2+1| \, |z^2+9| \geq ||z^2|-1| \, ||z^2| – 9| =(R^2-1) (R^2-9).
\end{equation*}
Entonces, de la proposición 34.3(5) tenemos que:
\begin{align*}
\left| \int_{C_R} \frac{1}{(z^2+1)(z^2+9)} dz \right| & \leq \int_{C_R} \frac{1}{|(z^2+1)(z^2+9)|} |dz|\\
& \leq \frac{1}{(R^2-1)(R^2-9)} \int_{C_R} |dz|\\
& = \frac{1}{(R^2-1)(R^2-9)} \ell(C_R)\\
& = \frac{\pi R}{(R^2-1)(R^2-9)},
\end{align*}de donde:
\begin{equation*}
\lim_{R\to\infty} \left| \int_{C_R} \frac{1}{(z^2+1)(z^2+9)} dz \right| \leq \lim_{R\to\infty} \frac{\pi R}{(R^2-1)(R^2-9)} = 0.
\end{equation*}
Por lo tanto:
\begin{equation*}
\text{P.V.} \displaystyle \int_{-\infty}^{\infty} \frac{1}{(t^2+1)(t^2+9)} dt= \lim_{R \to \infty} \int_{-R}^{R} \frac{1}{(t^2+1)(t^2+9)} dt = \frac{\pi}{12}.
\end{equation*}
Tarea moral
- Evalúa la siguientes integrales, donde la circunferencia $C(z_0,R)$ está orientada positivamente.
a) $\displaystyle\int_{C(0,3)} \dfrac{dz}{z^4+z^3-2z^2}$.
b) $\displaystyle\int_{C(0,1)} \dfrac{z^2+3z-1}{z(z^2-3)} dz$.
c) $\displaystyle\int_{C(0,3)} \dfrac{z^2+1}{(z-1)^2}dz$.
d) $\displaystyle\int_{C(0,1/10)} \dfrac{dz}{z^5-1}$. - Muestra que:
\begin{equation*}
\int_{0}^{2\pi} \frac{dt}{1+\operatorname{cos}^3(t)} = \pi.
\end{equation*} - Determina el residuo de la función $f(z) = \dfrac{\pi \operatorname{cot}(\pi z)}{z^2}$ en $z_0 = 0$.
- En cada caso determina el residuo de cada función en todas sus singularidades aisladas.
a) $f(z) = \dfrac{1+z}{z}$.
b) $f(z) = \operatorname{csc}(\pi z)\dfrac{z+1}{z-1}$.
c) $f(z) = \dfrac{1+z}{z^2+2z+2}$.
d) $f(z) = \dfrac{\operatorname{sen(z^2)}}{z^2(z^2+1)}$. - Verifica que:
\begin{equation*}
\int_{0}^{2\pi} \frac{\operatorname{cos}(2t) dt}{5-4\operatorname{cos}(t)} = \frac{\pi}{6}.
\end{equation*} - Prueba que $\operatorname{Res}(f+g,z_0) = \operatorname{Res}(f,z_0) + \operatorname{Res}(g,z_0)$.
- Prueba que si $f$ tiene un polo simple en $z_0$ y $g$ es analítica en $z_0$, entonces:
\begin{equation*}
\operatorname{Res}(f(z)g(z),z_0) = g(z_0)\operatorname{Res}(f(z),z_0).
\end{equation*} - Muestra que:
\begin{equation*}
\text{P.V.} \int_{-\infty}^{\infty} \frac{1}{(t^2+1)(t^2+4)} dt= \frac{\pi}{6}.
\end{equation*}
Más adelante…
Esta entrada es la última de estas notas. En ella hemos definido lo que es un residuo de una función analítica y establecimos algunos resultados que nos permiten su cálculo. En particular abordamos el Teorema del Residuo y vimos algunas aplicaciones de este resultado para evaluar integrales reales.
Como es bien sabido, la teoría de la Variable Compleja es muy extensa, por lo que existen muchas otras aplicaciones de la misma, que resultan muy útiles para resolver problemas relacionados con Ecuaciones Diferenciales, Transformadas de Laplace, Transformadas de Fourier, entre otros tantos. Sin embargo, debido a lo extenso de dichos temas, tales aplicaciones se escapan del objetivo de estas notas, pero pueden consultarse sobre ellas en la bibliografía de estas notas.
Entradas relacionadas
- Ir a Variable Compleja I.
- Entrada anterior del curso: Clasificación de ceros y singularidades de una función analítica.