Introducción
Inducción y recursión son dos conceptos similares con los que seguramente te has topado en tu formación matemática, e incluso tal vez antes. Muchas veces se llegan a confundir ambos conceptos, ya que ambos tienen una fuerte relación con el 5° axioma de Peano.
Aunque lo detallaremos a lo largo de la entrada, el principio de Inducción es una propiedad de los números naturales, que nos sirve para demostrar que todos los naturales satisfacen una propiedad. Es decir, es una estrategia de demostración. En contraste, la recursión es un resultado que justifica el hecho de poder dar una definición para todos los naturales, basándonos en la definición de su antecesor. En otras palabras, es una estrategia de definición.
Al final de la entrada demostraremos el teorema de recursión débil, en cuya prueba, podremos apreciar cómo es que depende directamente del Principio de inducción.
Pruebas por inducción
Recordemos el 5° axioma de Peano, el cual probamos en la entrada pasada que se satisface en nuestro modelo:
Si $S\subset \mathbb{N}$ satisface que
- $0\in S$ y
- si $n\in S$, implica que $\sigma(s)\in S$,
entonces $S=\mathbb{N}$.
Como hemos mencionado en entradas anteriores, esta proposición es muy similar al principio de Inducción que probablemente hayas ocupado desde el curso de Álgebra Superior I. Más aún, en la entrada pasada, seguimos la misma estrategia que en otros cursos, a la hora de ocupar el 5° axioma. Efectivamente, la equivalencia entre ambos resultados es casi inmediata, y como ejemplo ilustrativo, probaremos el Principio de Inducción a partir del 5° axioma de Peano.
Proposición (Principio de Inducción): Sea $P(n)$ una propiedad, es decir, una proposición matemática que depende de un entero $n$. Si se tiene que:
- $P(0)$ es verdadera y
- cada vez que $P(n)$ es cierto, también lo es $P(n+1)$,
entonces P(n) es cierta para todos los números naturales.
Demostración. Sea $P(n)$ una propiedad que satisface 1. y 2. y consideremos el conjunto $S:=\{n\in\mathbb{N}: P(n)\text{es verdadera}\}$.
Como $P(0)$ es verdadera, entonces $0\in S$.
Tomemos $n\in S$, entonces $P(n)$ es verdadera, y por 2., tenemos que $P(n+1)$ es verdadera; es decir, $n+1\in S$. Por el 5° Axioma de Peano, se tiene que $S=\mathbb{N}$, por lo que por la definición de $S$, se tiene que $P(n)$ es cierta para cada $n\in \mathbb{N}$
$\square$
Definiciones por recursión
Una de nuestras primeras ideas para poder construir a $\mathbb{N}$, fue intentar construir a mano cada elemento. Para esto, dimos una definición de lo que significaba el $0$ y el sucesor de un número. Después empezamos a iterar una y otra vez la función sucesor para obtener el sucesor del último número encontrado. Discutimos por qué es que esta idea no sería el mejor camino (sólo nos permite llegar hasta una cantidad finita de naturales), por lo tuvimos que introducir el Axioma del Infinito para resolver el problema. Veamos la analogía entre esta idea y el siguiente ejemplo intuitivo.
Ejemplo: Definamos la función factorial de un número natural, como:
- $0!=1$
- $(n+1)!=(n!)(n+1)$
Entonces, $3!:=(2!)(3)=(1!)(2)(3)=(0!)(1)(2)(3)=(1)(1)(2)(3)=6$.
Recordemos que al definir a los naturales, necesitábamos conocer un número para poder definir su sucesor. Aquí sucede lo mismo: en la definición de factorial necesitamos conocer quién es el factorial de un número para poder definir el factorial de su sucesor. A este tipo de definiciones se les conoce como definiciones recursivas, ya que para definir algo para un número, necesitamos tener conocimiento del valor de la función en los números anteriores.
Queda una pregunta muy importante. Si a los naturales no los pudimos definir de manera recursiva, ¿por qué podemos afirmar que la función factorial sí existe? A continuación enunciaremos algunos teoremas que nos garantizarán que sí podemos hacer este tipo de definiciones recursivas en nuestro modelo. Daremos una versión fuerte y una versión débil. Demostraremos la versión débil, pues basta para mucho de lo que queremos definir en los naturales (sumas, productos, potencias).
Las siguientes secciones son un poquito técnicas. Si las puedes seguir por completo, es fantástico. Pero incluso si no es así, basta con que en el fondo te quedes con la idea importante detrás: sí se vale definir de manera recursiva. Más adelante podrás regresar a este tema y entenderlo por completo.
Los teoremas de la recursión
Antes de la demostración principal de esta entrada, enunciaremos los teoremas que nos importan y hablaremos de manera intuitiva de lo que dicen. Hay dos versiones que veremos: una fuerte y una débil. Aunque parece que dicen cosas diferentes, en realidad son equivalentes. Será muy claro que la versión fuerte «implica» a la débil. Pero luego, en los problemas de tarea moral, se esbozará cómo ver que la versión débil se puede utilizar para demostrar la fuerte.
Teorema (Recursión Fuerte): Sea $X$ un conjunto y $x_{0}\in X$. Supongamos que tenemos varias funciones (una por cada natural $i$)
$$\{f_i:X\to X\}_{i\in\mathbb{N}\setminus \{0\}}.$$
Entonces existe una única función $g:\mathbb{N}\to X$ tal que:
- $g(0)=x_{0}$
- $g(\sigma(n))=f_{\sigma(n)}(g(n))$.
¿Qué es lo que quiere decir este teorema? Para responder esta pregunta veamos el siguiente diagrama:
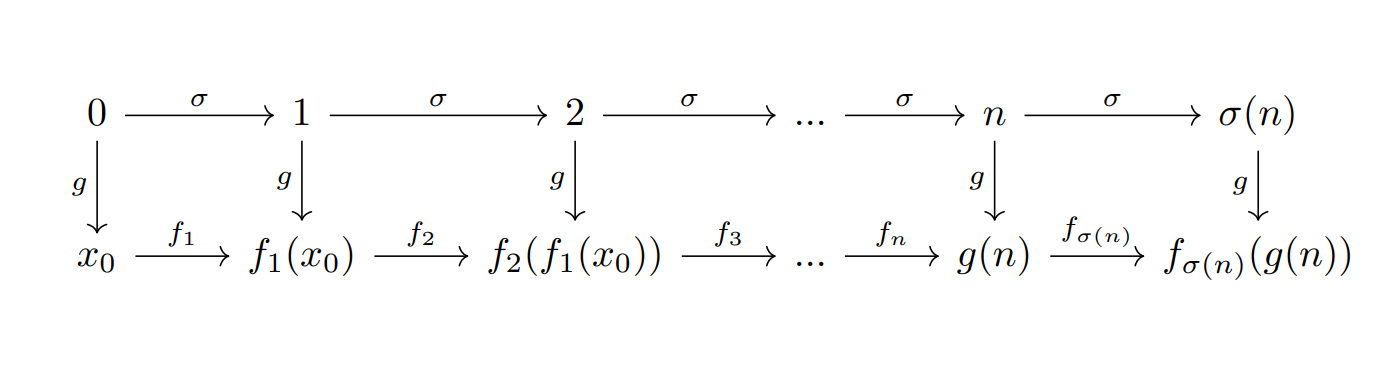
Nuestro diagrama empieza en $0$, el cual queremos que sea mandado a algún $x_{0}\in X$, para la definición de los demás números, ocupamos la segunda característica que esperamos que $g$ satisfaga. Por ejemplo $g(1)=g(\sigma(0))=f_{1}(g(0))=f_{1}(x_{0})$. Este análisis coincide con lo que nos presenta el primer cuadro de flechas del diagrama anterior, que nos presenta los dos caminos que debe satisfacer $g$, para que sea la función que queremos. Como da lo mismo si «primero aplicamos $\sigma$ y luego $g$», a que si «primero aplicamos $g$ y luego $f_1$», decimos que el primer cuadrado del diagrama conmuta.
Análogamente, ya que conocemos la definición de $g(1)$ podemos fijarnos en el segundo cuadro, para poder definir $g(2)$ (de nuevo, conmuta) y seguir «recursivamente» para cualquier número natural.
Ejemplo: ¿Qué conjunto, y qué funciones necesitamos para definir el factorial?
Consideremos $X=\mathbb{N}$, definiremos intuitivamente (ya que aún no lo hemos definido formalmente), $f_{i}:\mathbb{N}\longrightarrow \mathbb{N}$, como $f_{i}(n)=i\cdot n$, es decir, el producto por $i$.
El teorema de Recursión Fuerte, nos dice que existe una única función $g$ tal que
- $g(0)=1$
- $g(\sigma(n))=f_{\sigma(n)}(g(n))=\sigma(n)\cdot g(n)$
Denotemos $n!:=g(n)$. Entonces tenemos que $\sigma(n)!=n!\cdot \sigma(n)$, justo como queremos.
$\triangle$
El teorema de Recursión Débil y su demostración
El teorema de Recursión Débil tiene un enunciado parecido al teorema de recursión fuerte y puede ser visto como una consecuencia directa del teorema anterior pues se obtiene de la versión fuerte tomando $f_{1}=f_{2}=\ldots=f_{n}=\ldots$
Teorema (Recursión Débil): Sea $X$ un conjunto y $x_{0}\in X$. Supongamos que tenemos una función $f:X\to X$. Entonces existe una única función $g:\mathbb{N}\to X$ tal que:
- $g(0)=x_{0}$
- $g(\sigma(n))=f(g(n))$.
Para concluir con esta entrada, probaremos el teorema de Recursión Débil. Antes de hacer esto introducimos un concepto auxiliar y una propiedad de los naturales.
Recordemos que como conjunto, $m=\{0,1,…,m-1\}$, lo que sugiere la siguiente definición.
Definición: Si $n,m\in \mathbb{N}$, decimos que $n<m$ si $n\in m$.
Puede probarse que esta relación en $\mathbb{N}$ es un orden total, y que sastisface la siguiente propiedad.
Teorema (Principio el Buen Orden): Sea $S\subset\mathbb{N}$ un conjunto no vacío, es decir $S\neq \emptyset$. Entonces $S$ tiene un elemento mínimo. Es decir, existe $n\in S$ tal que $n<m$ para todo $m\in S\setminus\{n\}$.
La prueba del Principio del Buen Orden y más propiedades de $<$ serán estudiadas con mayor detalle en entradas posteriores. Con esto en mente demostramos el teorema de Recursión Débil.
Demostración. Recordemos que por definición, toda función con dominio $A$ y codominio $B$, es un subconjunto de $A\times B$, por lo que una buena idea es analizar el conjunto $\wp(\mathbb{N}\times X)$, definamos
\[\Re:=\{R\in\wp(\mathbb{N}\times X)\mid (0,x_{0})\in R \text{ y si }(n,x)\in R\text{, entonces }(\sigma(n),f(x))\in R\}\]
Esta definición se ve terriblemente complicada. Pero la intuición es clara: $\Re$ tiene a todas las posibles colecciones de parejas de $\mathbb{N}\times X$ que cumplen lo que queremos. El problema es que muchas de ellas no son funciones y tenemos que «arreglar esto».
Probablemente, notarás alguna similitud entre el conjunto $\Re$ y el conjunto de los subconjuntos inductivos (que se menciona en La construcción de los naturales). Siguiendo esta analogía, definiremos $g:=\bigcap \Re$ (podemos hacer esta intersección ya que $\Re$ no es vacío pues $\mathbb{N}\times X$ está en $\Re$).
- Demostremos que $g\in \Re$:
Por las propiedades de la intersección, tenemos que $g\subset\mathbb{N}\times X$, por lo que $g\in \wp(\mathbb{N}\times X)$. Veamos que $(0,x_{0})\in g$. Sea $R\in\Re$ arbitrario, entonces $(0,x_{0})\in R$, por lo que $(0,x_{0})\in\bigcap \Re=g$. Por último, si $(n,x)\in g$, demostremos que $(\sigma(n),f(x))\in g$, para esto, sea $R\in \Re$ arbitrario, como $(n,x)\in g$, entonces $(n,x)\in R$, por lo que $(\sigma(n),f(x))\in R$. Es decir, $(\sigma(n), f(x))\in\bigcap \Re=g$. Por todo lo anterior, $g\in\Re$.
- Veamos ahora que $Dom(g)=\mathbb{N}$:
Usemos el quinto axioma de Peano, como $(0,x_{0})\in g$, entonces $0\in Dom(g)$. Supongamos ahora que $n\in Dom(g)$ y demostremos que $\sigma(n)\in Dom(g)$, por la hipótesis de inducción, existe $x\in X$ tal que $(n,x)\in g$, y como $g\in\Re$, tenemos que $(\sigma(n),f(x))\in g$, pero esto quiere decir que $\sigma(n)\in Dom(g)$. Entonces $Dom(g)$ es inductivo, entonces $Dom(g)=\mathbb{N}$.
- Demostremos ahora que $g$ sí es función. Para esto, tenemos ver que «cada natural se va a un sólo elemento», en símbolos, si $(n,x),(n,y)\in g$ entonces $n=m$.
Aquí es donde ocuparemos el Principio del Buen Orden. Consideremos $S:=\{n\in\mathbb{N}\mid (n,x),(n,y)\in g \text{ y } x\neq y \}$. Procedamos por contradicción, supongamos que $S\neq\emptyset$, entonces, $S$ tiene un elemento mínimo, denotémoslo por $n$.
Si $n=0$, entonces existe $x\in X$ tal que $(0,x)\in X$ y $x\neq x_{0}$. Entonces consideremos $g’=g\setminus\{(0,x)\}$. Notemos que $g’\in\Re$, ya que $(0,x_{0})\in g’$, ya que $(0,x_{0})\neq (0,x)$. Además si $(k,a)\in g’$, entonces $(k,a)\in g$, por lo que $(\sigma(k),f(a))\in g$, y como $0$ nunca es el sucesor de otro número, tenemos que $(\sigma(k),f(a))\neq(0,x)$, por lo tanto $(\sigma(k),f(a))\in g’$, es decir, $g’\in \Re$, lo que implica que $g=\bigcap \Re\subset g’=g\setminus\{(0,x)\}$ lo cual es absurdo, por lo que $n\neq 0$.
Como $n\neq 0$, debemos tener que existe $m$ tal que $\sigma(m)=n$ ¿Por qué?. Y como $n$ es el mínimo en $S$, tenemos que $m\not\in S$, es decir, existe un único $x\in X$ tal que $(m,x)\in g$, esto implica que $(\sigma(m),f(x))=(n,f(x))\in g$, y como $n\in S$, debe existir $y\in X$, $y\neq f(x)$ tal que $(n,y)\in g$. Análogamente a como lo hicimos antes, consideremos $g’=g\setminus (n,y)$ y veamos que $g’\in \Re$. Como $(n,y)\neq(0,x_{0})$, tenemos que $(0,x_{0})\in g’$. Más aún, si $(k,a)\in g’$, demostremos que $(\sigma(k),f(a))\in g’$, para esto supongamos que no.
Como $(k,a)\in g’$, tenemos que $(k,a)\in g$, por lo que $(\sigma(k),f(a))\in g$, esto implica que $(\sigma(k),f(a))=(n,y)$ ya que este es el único elemento de $g$ que no está en $g’$. Como $\sigma(k)=n=\sigma(m)$, concluimos, por la inyectividad de $\sigma$, que $k=m$. Esto quiere decir que $(k,a)=(m,a)\in g$, pero recordando que $x$ es el único elemento relacionado con $m$, concluimos que $x=a$, en síntesis, $(k,a)=(m,x)$, por lo que $(\sigma(k),f(a))=(\sigma(m),f(x))=(n,f(x))\neq(n,y)$. Esto implica que $(\sigma(k), f(a))\in g’$, contradiciendo nuestra suposición de que no lo estaba.
Entonces hemos probado que $(0,x_{0})\in g’$ y que cada vez que $(k,a)\in g’$, también lo está $(\sigma(k), f(a))$. Esto quiere decir que $g’\in\Re$, y como lo hicimos anteriormente, tendremos que $g=\bigcap \Re\subset g’=g\setminus\{(n,y)\}$, lo cual es una contradicción. Esto quiere decir, que suponer que $S$ tiene un elemento mínimo, es absurdo, por lo que $S=\emptyset$. Lo que traducido quiere decir que para todo $n\in\mathbb{N}$, existe un único $x\in X$ tal que $(n,x)\in g$. Es decir, que $g$ sí es una función.
- Demostremos que $g$ satisface las dos propiedades del Teorema.
Ya vimos que $g\in \Re$, por lo que $g(0)=x_{0}$. Sea ahora $n\in \mathbb{N}$ y $x=g(n)$, de nuevo, como $g\in\Re$, tenemos que $g(\sigma(n))=f(x)=f(g(n))$.
- Por último, demostremos la unicidad de $g$.
Si $h:\mathbb{N}\longrightarrow X$ es otra función que satisface las características del Teorema, consideremos $A=\{n\in\mathbb{N}\mid h(n)=g(n)\}$, como $h(0)=x_{0}=g(0)$. Tenemos que $0\in A$. Supongamos que $n\in A$. Tendríamos entonces que $h(\sigma(n))=f(h(n))=f(g(n))=g(\sigma(n))$, es decir que $\sigma(n)\in A$, por lo que $A$ es inductivo, y por consiguiente, $A=\mathbb{N}$. En resumen, $h$ y $g$, coinciden en dominio, codominio y regla de correspondencia, entonces $h=g$, como debíamos probar.
$\square$
La demostración del teorema de Recursión Fuerte requiere de algunos detalles adicionales, pero puede deducirse del teorema de Recursión Débil. Dejamos esto como uno de los problemas de la tarea moral.
Más adelante…
El teorema de Recursión será la mayor herramienta que tendremos para poder darle una forma más familiar a los números naturales, ya que las operaciones de suma y multiplicación, que veremos en la siguiente entrada, tendrán una definición recursiva.
Y así como el teorema de la Recursión nos permitirá definir, usaremos continuamente el principio de Inducción para poder demostrar las numerosas propiedades que estas operaciones tienen.
Tarea moral
A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.
- Demuestra el 5° Axioma de Peano a partir del Principio de Inducción.
- Demuestra que si $n\neq 0$ entonces existe $m$ tal que $\sigma(m)=n$.
- ¿Qué función $g$, satisface que $g(0)=1$ y $g(\sigma(n))=2\cdot g(n)$? ¿Qué función $f$ estamos ocupando?
- ¿Qué conjunto y que función nos permitiría definir la sucesión de Fibonacci $a_{n+2}=a_{n+1}+a_{n}$ usando el Teorema de Recursión?
- Demuestra el Teorema de Recursión Fuerte, usando el Débil. Sugerencia: Considera, $F(n,x):\mathbb{N}\times X\longrightarrow \mathbb{N}\times X$, como $F(n,x)=(\sigma(n),f_{\sigma(n)}(x))$.
Entradas relacionadas
- Ir a: Álgebra Superior II
- Entrada anterior del curso: La construcción de los naturales
- Entrada siguiente del curso: Definición de suma y propiedades básicas
Agradecimientos
Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»
