(Trabajo de titulación asesorado por la Dra. Diana Avella Alaminos)
Introducción
Ahora sí, comenzaremos con el tema de este curso. Después de estudiar las operaciones binarias por fin veremos para qué nos sirven. Los grupos son una estructura algebraica. Están constituidos por dos partes, un conjunto y una operación ¿Puedes imaginarte de qué tipo de operación estamos hablando?
Para motivarlo, veamos cómo resolvemos esta ecuación:
\begin{align*}
x+8 & = 5\\
(x + 8) + (-8) &= 5 + (-8)\\
x + 0 &= -3\\
x &= -3.
\end{align*}
Al resolver la ecuación, formalmente estamos usando las siguientes propiedades:
- Asociatividad.
- Inverso aditivo.
- Neutro.
En ese mismo orden.
En esta entrada definiremos formalmente a los grupos y daremos muchos ejemplos para que te empapes de la definición. Revisaremos los ejemplos que vimos en entradas anteriores y determinaremos cuáles son un grupo y cuáles no.
¿Qué es un grupo?
Definición. Sea $G$ un conjunto con una operación binaria $*$. Decimos que $(G,*)$ es un grupo si
- La operación $*$ es asociativa, es decir, $(a * b)*c = a*(b*c) \quad \forall a,b,c \in G$
- Existe $e \in G$ tal que $e*a = a*e = a \quad \forall a \in G$.
A $e$ se le llama neutro en $G$. - Para toda $a \in G$ existe $\tilde{a} \in G$ tal que $a*\tilde{a} = \tilde{a}*a=e$.
En este caso, $\tilde{a}$ se llama inverso de a.
Si además * es conmutativa, es decir $a*b = b*a \quad \forall a,b \in G$, decimos que $(G,*)$ es un grupo abeliano.
Nota. Sea $G$ conjunto con una operación binaria $*$:
- Si $G \neq \emptyset$, $(G,*)$ se llama magma.
- Si $G\neq \emptyset$ y se cumple 1, $(G,*)$ se llama semigrupo.
- Si se cumplen 1 y 2, $(G,*)$ se llama monoide.
Repaso de ejemplos anteriores
Veamos de nuevo algunos ejemplos de las entradas anteriores y comprobemos si cumplen con la definición de grupo.
- $G : = \z^+$, $a*b = \text{máx}\{a,b\}$.
- En la entrada anterior vimos que $*$ es asociativa y conmutativa.
- $1$ es el neutro.
Demostración. $1*a = a*1 = \text{máx}\{1,a\} = a \quad \forall a \in \z^+$. $\blacksquare$ - $2$ no tiene inverso.
Demostración. $2*a = \text{máx}\{2,a\} \geq 2 \quad \forall a \in \z^+$, por lo que $2 * a \neq 1 \quad a \in \z^+$.
$\therefore (\z^+,*)$ NO es un grupo. $\blacksquare$
- $G:= \z^+$, $a*b = a$.
- No tiene neutro, si existiera $e \in \z^+$ neutro, entonces para toda $a\in\z^+$, por la definción de la operación $e*a = e$, pero la definición de neutro requiere que $e*a = a$. Entonces, esto implica que $e = a$ y como esto no es necesariamente cierto, pues $a$ es un entero positivo cualquiera, obtenemos una contradicción.
$\therefore (\z^+,*)$ NO es un grupo. $\blacksquare$
- $(\cM_{2\times 2}(\z), +)$ es un grupo abeliano, la demostración queda como ejercicio.
- $(\{ f \; | \; f:\r \to \r\}, \circ)$ no es un grupo, pues aunque $\mathrm{id}_{\r}$ es neutro, no todo elemento tiene inverso. Esto porque no toda función es biyectiva, como se ve en Álgebra Superior I.
- $(S_3, \circ)$ es un grupo no abeliano. Generalizaremos este ejemplo más adelante y le llamaremos grupo simétrico.
- $\cS = \{2,4,6\}$ con la operación
| $*$ | $2$ | $4$ | $6$ |
| $2$ | $2$ | $4$ | $6$ |
| $4$ | $4$ | $4$ | $6$ |
| $6$ | $6$ | $6$ | $6$ |
Si observamos la tabla, podemos concluir que:
- $2$ es neutro.
- $4$ y $6$ no tienen inversos.
Por lo tanto, NO es un grupo.
$\blacksquare$
- $\cS = \{2,4,6\}$ con la operación
| $*$ | $2$ | $4$ | $6$ |
| $2$ | $2$ | $2$ | $2$ |
| $4$ | $4$ | $4$ | $4$ |
| $6$ | $6$ | $6$ | $6$ |
- No hay un neutro.
Como no hay neutro, ni siquiera tiene sentido pensar en la existencia de inversos. Por lo tanto, NO es un grupo.
$\blacksquare$
- $\cS = \{1,-1\}$ con la operación
| $*$ | $1$ | $-1$ |
| $1$ | $1$ | $-1$ |
| $-1$ | $-1$ | $1$ |
- El $1$ es el neutro.
- La operación es asociativa.
- $1$, $-1$ son sus propios inversos.
- Además, la operación conmuta, porque la operación es el producto usual.
Por lo tanto es un grupo abeliano.
$\blacksquare$
- $(\z, +)$ es un grupo.
- Sea $K$ un campo y $K^* = K \setminus \{0_K\}$. Si consideramos $(K^*, \cdot)$ tenemos un grupo abeliano. Le quitamos el $0_K$ pues es el único número que no tiene inverso multiplicativo.
- $\mathbb{S}’ = \{z \in \mathbb{C} \; |\; |z|= 1\}$. Es decir, los complejos con norma igual a $1$. Es un grupo abeliano con el producto.
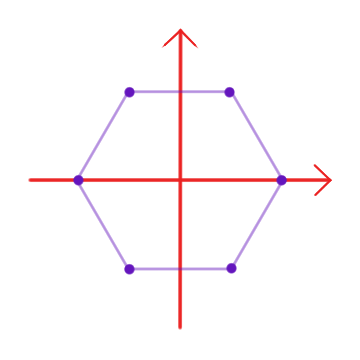
- Dentro de los complejos podemos considerar $$\Gamma_n = \left\{ \xi^k \; | \; 0 \leq k < n \text{, con } \xi = e^{\frac{2\pi i}{n}} \right\}.$$ Geométricamente corresponden a los vértices de un polígono regular de $n$ lados y algebraicamente son las raíces $n$-ésimas de la unidad. Forman un grupo abeliano con el producto.
Ejemplos importantes de matrices
Los siguientes son ejemplos de algunos grupos importantes. Recuérdalos porque son ejemplos que serán recurrentes en futuras entradas. Recuerda que no todas las matrices tienen inverso multiplicativo y que el producto de matrices no es conmutativo. Para refrescar tu memoria, puedes consultar las entradas de matrices inversas y operación de matrices.
- $$GL(n,\r) = \{A \in \cM_{n\times n}(\r) \;|\; \det A \neq 0\},$$ con el producto usual es un grupo no abeliano. Este par ordenado $(GL(n,\r), \cdot)$ es conocido como el grupo lineal general de matrices $n\times n$ con coeficientes en $\r$.
- $$SL(n,\r) = \{A \in \cM_{n\times n}(\r) \;|\; \det A = 1\},$$ con el producto usual es un grupo no abeliano. Este es el grupo lineal especial de matrices $n\times n$ con coeficientes en $\r$.
- $$SO(n,\r) = \{A \in \cM_{n\times n}(\r) \; | \; AA^t = I_n, \; \det A = 1\},$$ con el producto usual es un grupo no abeliano. A éste se le conoce como grupo ortogonal especial de matrices $n\times n$ con coeficientes en $\r$.
- $$O(n, \r) = \{A \in \cM_{n\times n}(\r) \; |\; AA^t = I_n\},$$ con el producto usual es un grupo no abeliano. Este es conocido como el grupo ortogonal de matrices $n\times n$ con coeficientes en $\r$.
Tarea moral
A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.
- Determina, en cada uno de los siguientes casos, si el sistema descrito es grupo o no. En caso negativo, señala cuál o cuáles de los axiomas de grupo no se verifican. En caso afirmativo demuestra que es un grupo:
- $G = \r \setminus \{-1\}$, $a*b := a+b+ab$.
- $G = \r^*$, $a*b = |a|b$.
- $G = \{r \in \mathbb{Q} \;|r\text{ se puede expresar como }\; r = \frac{p}{q} \text{ con } (p,q)= 1 \text{ y } q \text{ impar}\}$, $a*b = a+b$ (la adición usual).
- Sea $X$ un conjunto. Considera $G = \mathcal{P}(X)$ el conjunto potencia de $X$ con la operación binaria $A \triangle B = (A \cup B)\setminus (A \cap B)$ para todo $A,B \in \mathcal{P}(X)$.
- Demuestra la siguientes afirmaciones referentes a grupos, dadas en los ejemplos anteriores:
- $(\cM_{2\times 2}(\z), +)$ es un grupo abeliano.
- $(S_3, \circ)$ es un grupo no abeliano.
- $(\z, +)$ es un grupo.
- $(K^*, \cdot)$ con $K$ un campo, es un grupo abeliano.
- $(\Gamma_n, \cdot)$ es un grupo abeliano, con $\cdot$ el producto.
- Demuestra por qué los ejemplos importantes de matrices son grupos no abelianos.
Más adelante…
Después de tantas definiciones y ejemplos, comenzaremos a ver más teoremas y demostraciones. En la siguiente entrada profundizaremos en las propiedades de grupos derivadas de su definición. Además, veremos un teorema conocido como la «Definición débil de Grupo».
Entradas relacionadas
- Ir a Álgebra Moderna I.
- Entrada anterior del curso: Operación binaria asociativa y conmutativa.
- Siguiente entrada del curso: Propiedades de grupos y Definición débil de grupo.
- Resto de cursos: Cursos.