Introducción

Si tenemos dos conjuntos $X$ y $Y$ y se nos pide definir una función $f:X\to Y$ lo que debemos hacer es relacionar a cada uno de los elementos de $X$ con un único elemento de $Y$. Esta forma de proceder no garantiza que cualquier elemento de $Y$ se encuentra relacionado con algún elemento de $X$. Aquellas funciones que sí cumplan esto último les llamaremos funciones suprayectivas y será el tema que trataremos en esta entrada.

Función suprayectiva

Definición. Sea $f:X\to Y$ una función. Si $f[X]=Y$, entonces decimos que $f$ es suprayectiva.

$\square$

Teorema. ¹Sea $f:X\to Y$ una función. Entonces los siguientes enunciados son equivalentes:

1. $f$ es suprayectiva.
2. Para cualquier $y\in Y$, existe $x\in X$ tal que $f(x)=y$.
3. Para cualesquiera $h,k:Y\to Z$ tales que $h\circ f= k\circ f$, se tiene que $h=k$.

Demostración.

$1)\rightarrow 2)$

Supongamos que $f$ es suprayectiva, es decir que $f[X]=Y$. Sea $y\in Y$, entonces $y\in f[X]$ por lo que existe $x\in X$ tal que $f(x)=y$. Por lo tanto, para cualquier $y\in Y$ existe $x\in X$ tal que $f(x)=y$.

$2)\rightarrow 3)$

Sean $h,k:Y\to Z$ tales que $h\circ f=k\circ f$. Veamos que $h=k$. Sea $y\in Y$, veamos que $h(y)=k(y)$. Dado que $y\in Y$, por hipótesis tenemos que existe $x\in X$ tal que $f(x)=y$, por lo que $h(y)= h(f(x))$ y $k(y)= k(f(x))$. Luego, como $(h\circ f)(x)= h(f(x))= k(f(x))= (k\circ f)(x)$, tenemos que $h(y)= k(y)$.

$3)\rightarrow 1)$

Observemos que $f[X]\subseteq Y$, por lo que resta probar que $Y\subseteq f[X]$. Definamos $h: Y\to \set{0,1}$ y $k: Y\to \set{0,1}$ funciones dadas por $h(y)=0$ para todo $y\in Y$ y

\begin{align*}
k(y) = \left\{ \begin{array}{lcc}
0 &  \text{si} & y\in f[X]\\
1 &  \text{si}  & y \notin f[X] \\
\end{array}
\right.
\end{align*}

respectivamente.

Sea $x\in X$, entonces $f(x)\in Y$ y así, $(h\circ f)(x)= h(f(x))=0$ y $(k\circ f)(x)= k(f(x))=0$. Por lo tanto, $h\circ f=k\circ f$ y, por hipótesis $h=k$.

Si tomamos $y\in Y$, $h(y)=k(y)$. Esto significa que $k(y)=0$, por lo tanto, debe ocurrir que $y\in f[X]$.

Algunas funciones suprayectivas

Ejemplo.

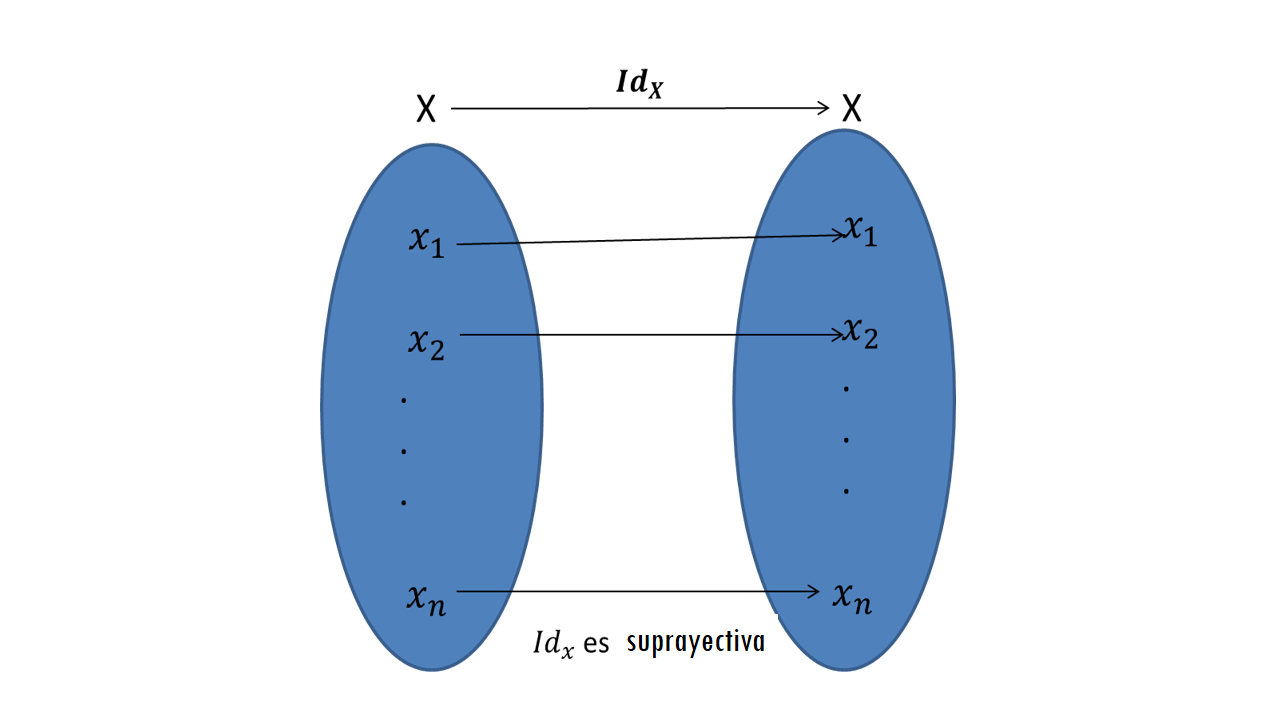
La función identidad es suprayectiva. En efecto, sea $Id_X:X\to X$ la función identidad y sea $y\in X$, entonces $y\in X$ satisface $Id_X(y)= y$.

Por lo tanto, $Id_X$ es suprayectiva.

$\square$

Ejemplo.

Sea $X$ un conjunto no vacío y $f:X\to \set{c}$ una función dada por $f(x)=c$ para todo $x\in X$. Tenemos que $f$ es suprayectiva.

Dado que $c$ es el único elemento de $\set{c}$, debemos encontrar que existe $x\in X$ tal que $f(x)=c$. Como $X$ no es vacío, existe $x\in X$ y es tal que que $f(x)=c$.

$\square$

Ejemplo.

Sea $X$ un conjunto y $A\subseteq X$ un subconjunto propio de $X$ (distinto de $X$ y no vacío). La función característica de $A$ es una función suprayectiva.

Deseamos ver que para cualquier $y\in \set{0,1}$ existe $x\in X$ tal que $\chi_A(x)=y$.

Caso 1: Si $y=0$, entonces tomemos $x\in X\setminus A$ de modo que $\chi_A(x)=0$.

Caso 2: Si $y=1$, entonces tomemos $x\in A$, de modo que $\chi_A(x)=1$.

Por lo tanto, $\chi_A$ es suprayectiva.

$\square$

Composición de funciones y suprayectividad

Así como lo hicimos en la entrada anterior con respecto a la inyectividad, también podemos averiguar qué pasa con la composición de funciones con respecto a la suprayectividad. Tenemos el siguiente teorema.

Teorema. Sean $f:X\to Y$ y $g:Y\to Z$ funciones suprayectivas, $g\circ f$ es suprayectiva.

Demostración.

Sea $z\in Z$, y veamos que existe $x\in X$ tal que $(g\circ f)(x)=z$.
Dado que $g$ es suprayectiva y $z\in Z$, entonces existe $y\in Y$ tal que $g(y)=z$. Luego, como $f$ es suprayectiva y $y\in Y$, entonces existe $x\in X$ tal que $f(x)=y$, así $z=g(y)=g(f(x))$. Por lo tanto, $g\circ f$ es suprayectiva.

$\square$

Funciones biyectivas

Definición. Decimos que $f:X\to Y$ es una función biyectiva si y sólo si $f$ es inyectiva y suprayectiva.

Ejemplo.

La función identidad es biyectiva.

Verificamos en la entrada de funciones inyectivas que la función identidad es una función inyectiva, además de que en esta entrada verificamos que es suprayectiva.

$\square$

Ejemplo.

Sean $X=\set{1,2,3}$ y $Y=\set{2,4,6}$ y sea $f:X\to Y$ la función dada por $f(x)=2x$. Tenemos que $f$ es inyectiva pues es una función uno a uno, es decir, elementos distintos van a dar a elementos distintos. Más explícitamente $1$ va a dar a $2$, $2$ a $4$ y $3$ a $6$.

Además $f$ es suprayectiva, pues para cualquier $y\in Y$, existe $x\in X$ tal que $f(x)=y$. En efecto, esto sucede ya que para $2\in Y$ existe $1\in X$ tal que $f(1)=2$; para $4\in Y$ existe $2\in X$ tal que $f(2)=4$ y por último para $6\in Y$ existe $3\in X$ tal que $f(3)=6$.

$\square$

Tarea moral

Realiza la siguiente lista de ejercicios que te ayudará a fortalecer los conceptos de función inyectiva, suprayectiva y biyectiva.

1. Sean $f:X\to Y$ y $g:Y\to Z$ funciones. Demuestra que si $g\circ f$ es suprayectiva, entonces $g$ es suprayectiva.
2. Demuestra o da un contraejemplo del siguiente enunciado: Si $f:X\to Y$ y $g:Y\to Z$ son funciones tales que $g\circ f$ es suprayectiva, entonces $f$ es suprayectiva.
3. Sean $X=\set{1,2,3, \cdots}$ y $Y=\set{3,4,5,\cdots}$ y sea $f:X\to Y$ dada por $f(x)=2x+3$. ¿$f$ es suprayectiva? Argumenta tu respuesta. Quizás a estas alturas tengas que ser un poco informal en términos de teoría de conjuntos, pero usa lo que conoces de las operaciones de números.

Más adelante…

Ahora que aprendimos el concepto de función inyectiva y suprayectiva tenemos las bases suficientes para hablar de funciones invertibles. Veremos funciones invertibles por la derecha e invertibles por la izquierda, cuyos conceptos resultarán equivalentes al de función suprayectiva y función inyectiva respectivamente.

Entradas relacionadas

• Entrada relacionada: Funciones inyectivas y suprayectivas
• Ir a Teoría de los Conjuntos I
• Entrada anterior: Teoría de los Conjuntos I: Funciones inyectivas
• Siguiente entrada: Teoría de los Conjuntos I: Funciones inversas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE109323 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 3»

1. También puedes consultar la prueba de este teorema en: Hernández, F., Teoría de Conjuntos, México: Aportaciones Matemáticas No.13,
   SMM, 1998, p. 52-53 ↩︎