Introducción

En esta entrada abordaremos el concepto de función inyectiva. Una función inyectiva será aquella que relacione elementos distintos del dominio con elementos distintos del codominio.

Función inyectiva

Definición. Sea $f: X \to Y$. Decimos que $f$ es una función inyectiva si para cualesquiera $x_1$, $x_2 \in X$ tales que $x_1\not=x_2$, se tiene que $f(x_1)\not= f(x_2)$.

Ejemplo.

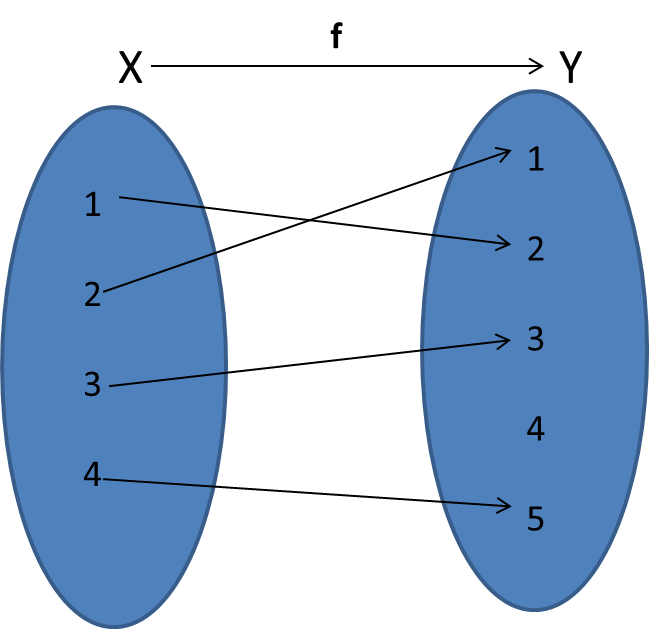
Sean $X=\set{1,2,3,4}$ y $Y=\set{1,2,3,4,5}$ y sea $f:X\to Y$ una función dada por $f=\set{(1,2), (2,1), (3,3), (4,5)}$. Decimos que $f$ es inyectiva pues cada elemento de $X$ bajo la función va a dar a un elemento distinto de $Y$, como se muestra en la siguiente imagen:

Ejemplo.

La función identidad es una función inyectiva.

En efecto, dado que $Id_X:X\to X$ esta dada por $Id_X(x)=x$, entonces si $x_1,x_2\in X$ son tales que $Id_X(x_1)=Id_X(x_2)$, entonces tendríamos $x_1=Id_X(x_1)=Id_X(x_2)=x_2$. Así, $x_1=x_2$ y por lo tanto $Id_X$ es inyectiva.

$\square$

Ejemplo.

La función constante no es inyectiva si su dominio tiene más de un elemento.

Consideremos $X=\set{1,2,3}$ y $Y=\set{1}$. Sea $f:X\to Y$ la función dada por $f(x)=1$ para toda $x\in X$. Consideremos $x_1=1$ y $x_2=2$ elementos de $X$. Sabemos que $1\not=2$ por lo que para que nuestra función sea inyectiva esperamos que $f(x_1)\not=f(x_2)$, sin embargo, $f(1)=1=f(2)$. Esto demuestra que, en general, las funciones constantes no son inyectivas.

$\square$

Equivalencias de inyectividad

Aunque la definición de inyectividad es muy intuitiva («mandar elementos distintos a elementos distintos»), en la práctica nos conviene tener una serie de equivalencias de esta definición que podamos usar en situaciones variadas.

Teorema.¹ Sea $f:X\to Y$ una función tal que $X\not=\emptyset$. Entonces los siguientes enunciados son equivalentes:

1. $f$ es inyectiva.
2. Para cualesquiera $x_1,x_2\in X$ si $f(x_1)=f(x_2)$, entonces $x_1=x_2$.
3. Para cualesquiera $h,k:Z\to X$ si $f\circ h= f\circ k$, entonces $h=k$.
4. Para cualesquiera $A,B$ subconjuntos de $X$, se cumple que $f[B\setminus A]= f[B]\setminus f[A]$.
5. Para cualesquiera $A,B$ subconjuntos de $X$ se cumple que $f[A\cap B]= f[A]\cap f[B]$.

Demostración.

$1)\rightarrow 2)$
Supongamos que $f$ es inyectiva, esto es, para cualesquiera $x_1, x_2\in X$ tales que $x_1\not=x_2$ se tiene que $f(x_1)\not=f(x_2)$. Luego, sabemos que la implicación es equivalente a la contrapositiva por lo que podemos concluir que para cualesquiera $x_1, x_2\in X$, si $f(x_1)=f(x_2)$ entonces $x_1=x_2$.

$2)\rightarrow 3)$
Supongamos que para cualesquiera $x_1, x_2\in X$ si $f(x_1)=f(x_2)$, entonces $x_1= x_2$ y supongamos que $h,k:Z\to X$ son funciones tales que $f\circ h= f\circ k$ y veamos que $h=k$.

Sea $z\in Z$, entonces $h(z)\in X$ y $k(z)\in X$, luego como $f\circ h=f\circ k$ tenemos que $(f\circ h)(z)= (f\circ k)(z)$, de donde $f(h(z))= f(k(z))$ y como $f$ es inyectiva entonces $h(z)=k(z)$. Por lo tanto, $h(z)=k(z)$ para todo $z\in Z$. Para concluir que $h=k$ notemos lo siguiente: $(z,y)\in h$ si y sólo si $h(z)=y$, lo cual ocurre si y sólo si $k(z)=y$, es decir, si y sólo si $(z,y)\in k$.

$3)\rightarrow 4)$

Supongamos que para cualesquiera $h,k:Z\to X$ se cumple que si $f\circ h= f\circ k$, entonces $h=k$. Sean $A,B$ conjuntos tales que $A\subseteq B\subseteq X$ y veamos que $f[B\setminus A]= f[B]\setminus f[A]$.

En la entrada de funciones vimos que siempre ocurre que $f[B]\setminus f[A]\subseteq f[B\setminus A]$ por lo que basta ver la otra contención.

Sea $y\in f[B\setminus A]$, entonces existe $x\in B\setminus A$ tal que $f(x)=y$. Tenemos que $x\in B$ y $x\notin A$, de modo que $f(x)\in f[B]$. Resta ver que $f(x)\notin f[A]$. Supongamos que sí ocurre, es decir que $f(x)\in f[A]$. Entonces existe $z\in A$ tal que $f(z)=f(x)$.

Definamos $h:X\to X$ dada por $h(a)=x$ para todo $a\in X$ y $k:X\to X$ dada por $k(a)=z$ para todo $a\in X$. Notemos que $h\not=k$ pues $z\not=x$ ya que $z\in A$ y $x\notin A$. Luego, $(f\circ h)(a)=f(h(a))= f(x)$ y $(f\circ k)(a)= f(k(a))= f(z)=f(x)$ para cada $a\in A$, por lo que $f\circ h=f\circ k$. Así, por hipótesis se sigue que $h=k$ lo cuál es una contradicción, por lo tanto, no debe ocurrir que $f(x)\in f[A]$. Así, $f(x)\in f[B]\setminus f[A]$.

$4)\rightarrow 5)$

Supongamos que para cualesquiera $A, B$ subconjuntos de $X$, se cumple que $f[B\setminus A]=f[B]\setminus f[A]$. Veamos que $f[A\cap B]= f[A]\cap f[B]$.

En la entrada de funciones probamos que $f[A\cap B]\subseteq f[A]\cap f[B]$, por lo que basta ver que $f[A]\cap f[B]\subseteq f[A\cap B]$.

Sea $y\in f[A]\cap f[B]$, entonces $y\in f[A]$ y $y\in f[B]$, así existe $x\in A$ tal que $f(x)=y$. Queremos demostrar que $x\in B$. Supongamos que no es así, es decir $x\notin B$. Por lo tanto, $x\in A\setminus B$ y $y=f(x)\in f[A\setminus B]= f[A]\setminus f[B]$.

Se sigue que $y\in f[A]$ y $y\notin f[B]$ lo cual es una contradicción. Por lo tanto, debe ocurrir que $x\in B$, así existe $x\in A\cap B$ tal que $f(x)=y$.

Por lo tanto, $f[A]\cap f[B]= f[A\cap B]$.

$5)\rightarrow 1)$

Supongamos que para cualesquiera $A, B\subseteq X$ se cumple que $f[A]\cap f[B]= f[A\cap B]$.

Sean $x_1, x_2\in X$ tales que $x_1\not= x_2$, veamos que $f(x_1)\not= f(x_2)$.

Consideremos $\set{x_1}$ y $\set{x_2}$ subconjuntos de $X$. Luego,

\begin{align*}
\emptyset&=f[\emptyset]\\
&=f[\set{x_1}\cap \set{x_2}]\\
&=f[\set{x_1}]\cap f[\set{x_2}]\ \text{por hipótesis}\\
&=\set{f(x_1)}\cap \set{f(x_2)}.
\end{align*}

Luego, como $\set{f(x_1)}\cap \set{f(x_2)}=\emptyset$, se tiene $\set{f(x_1)}\not=\set{f(x_2)}$ y por lo tanto, $f(x_1)\not=f(x_2)$.

Por lo tanto, $f$ es inyectiva.

Por lo tanto, todos los enunciados anteriores son equivalentes.

$\square$

Aunque existen muchas equivalencias de función inyectiva, para estas notas usaremos con mayor frecuencia la equivalencia dos del resultado anterior.

¿Qué pasa con la composición y la inyectividad?

Anteriormente vimos que la composición de funciones (pensándolas como relaciones) resulta ser una función. Podemos preguntarnos qué ocurre si las funciones que conforman a la composición son inyectivas. ¿Será que eso implica que la composición es inyectiva? Esto lo responde el siguiente teorema.

Teorema. Sean $f:X\to Y$ y $g:Y\to Z$ funciones inyectivas. Se cumple que $g\circ f$ es inyectiva.

Demostración.

Sean $f$ y $g$ funciones inyectivas y sean $x_1, x_2\in X$ tales que $(g\circ f)(x_1)= g(f(x_1))=g(f(x_2))= (g\circ f)(x_2)$. Dado que $f(x_1), f(x_2)\in Y$ y $g$ es inyectiva, entonces $ g(f(x_1))=g(f(x_2)) $ implica que $f(x_1)=f(x_2)$. Por la inyectividad de $f$ podemos concluir que $x_1=x_2$. Por lo tanto, $g\circ f$ es una función inyectiva.

$\square$

Tarea moral

La siguiente lista de ejercicios te permitirá reforzar el tema de funciones inyectivas.

• Demuestra que la función inclusión es inyectiva.
• Sean $A=\set{1,2,3}$, $B=\set{1,2}$ y $C=\set{1,2}$ conjuntos. Sean $f:A\to B$ y $g:B\to C$ funciones dadas por $f=\set{(1,1), (2,1), (3,2)}$ y $g=\set{(1,2), (2,1)}$ respectivamente. Escribe al conjunto $g\circ f$ y ve si la función correspondiente es inyectiva. Argumenta tu respuesta.
• Si $f\circ g$ es inyectiva, ¿es cierto que $f$ y $g$ son inyectivas? ¿Será cierto que por lo menos una de ellas siempre es inyectiva?
• Demuestra que la función $\emptyset$ es inyectiva.
• Demuestra que $f:X\to Y$ una función constante es inyectiva si y sólo si $X=\set{x}$ para algún conjunto $x$.

Más adelante…

En la siguiente entrada abordaremos el tema de funciones suprayectivas. Con este tema tendremos los conceptos necesarios para comenzar a hablar acerca de funciones biyectivas e invertibles.

Entradas relacionadas

• Entrada relacionada: Álgebra Superior I: Funciones inyectivas, suprayectivas y biyectivas
• Ir a Teoría de los Conjuntos I
• Entrada anterior: Teoría de los conjuntos I: Funciones (parte II)
• Siguiente entrada: Teoría de los Conjuntos I: Funciones suprayectivas y biyectivas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE109323 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 3»

1. También puedes consultar la prueba de este teorema en: Hernández, F., Teoría de Conjuntos, México: Aportaciones Matemáticas No.13, SMM, 1998, pp. 51-52. ↩︎